Vamos con los ejercicios del 31 al 40 del examen simulador de matemáticas para el examen de ingreso al IPN para el área de Ciencias Sociales y Administrativas.

En este punto, desarrollar tu capacidad de análisis es más importante que la cantidad de reactivos resueltos.
Reactivo 31
Una discontinuidad evitable es aquella que…
- Es continua en ese punto según la dirección de proximidad
- La función no es continua en ese punto
- El límite en el punto existe, pero la función evaluada es distinta al límite o no existe
- Los límites laterales nunca son diferentes
Solución:
En el estudio de la continuidad de funciones, decimos que una discontinuidad es evitable si su límite existe, pero la función evaluada en el punto es diferente al límite o no existe.
En dicho caso, se puede reescribir a la función como una función a trozos, de tal forma que en el punto de la discontinuidad sea igual al límite y para el resto del dominio f\left(x\right) .
f\left(x\right)=\left\{\begin{array}{c}f\left({x}_{o}\right)=\underset{x\to {x}_{o}}{\mathrm{lim}}f\left(x\right), x={x}_{o}\\ f\left(x\right), x\in R-\left\{{x}_{o}\right\}\end{array}\right.
La respuesta correcta es el inciso c).
Reactivo 32
Calcule la derivada de la siguiente función.
f\left(x\right)={e}^{{x}^{2}-1}
- {f}^{\text{'}}\left(x\right)={e}^{{x}^{2}-1}
- {f}^{\text{'}}\left(x\right)=x{e}^{{x}^{2}-1}
- {f}^{\text{'}}\left(x\right)=2x{e}^{{x}^{2}}
- {f}^{\text{'}}\left(x\right)=2x{e}^{{x}^{2}-1}
Solución:
Se trata de una función compuesta en la que, aplicando la regla de la cadena, determinamos que primero se aplica la fórmula de la derivada de la exponencial.
{f}^{\text{'}}\left(x\right)={\left[{e}^{{x}^{2}-1}\right]}^{\text{'}}={\left({x}^{2}-1\right)}^{\text{'}}{e}^{{x}^{2}-1}
Resolvemos la derivada indicada:
{\left({x}^{2}-1\right)}^{\text{'}}{e}^{{x}^{2}-1}=2x{e}^{{x}^{2}-1}
Finalmente:
{f}^{\text{'}}\left(x\right)=2x{e}^{{x}^{2}-1}
La respuesta correcta es el inciso d).
Reactivo 33
Calcule la pendiente de la asíntota oblicua por la derecha para la función g\left(x\right)=\frac{2{x}^{2}+x}{x-3}
- m=2
- m=0
- m=1
- m=-2
Solución:
En este caso, calculamos el siguiente límite para obtener la pendiente de la asíntota oblicua por la derecha de la función:
m=\underset{x\to \infty }{\mathrm{lim}}\frac{f\left(x\right)}{x}
Aplicado sobre la función nos queda:
m=\underset{x\to \infty }{\mathrm{lim}}\frac{\frac{2{x}^{2}+x}{x-3}}{x}=\underset{x\to \infty }{\mathrm{lim}}\frac{2{x}^{2}+x}{x\left(x-3\right)}
Iniciamos la solución extrayendo factor común x del numerador.
\underset{x\to \infty }{\mathrm{lim}}\frac{2{x}^{2}+x}{x\left(x-3\right)}=\underset{x\to \infty }{\mathrm{lim}}\frac{2x+1}{x-3}
Por regla general, los límites al infinito del cociente de polinomios con el mismo grado, tienen como resultado el cociente de los coeficientes de los términos de mayor grado:
\underset{x\to \infty }{\mathrm{lim}}\frac{2x+1}{x-3}=2
La pendiente de la asíntota oblicua por la derecha de g\left(x\right) es m=2 .
La respuesta correcta es el inciso a).
Reactivo 34
Encuentre la descomposición en fracciones parciales de la siguiente expresión.
\frac{1}{\left(x+1\right)\left(x+2\right)}
- \frac{1}{x+1}-\frac{2}{x+2}
- -\frac{1}{x+1}-\frac{1}{x+2}
- \frac{1}{x+1}-\frac{1}{x+2}
- \frac{1}{x+1}+\frac{1}{x+2}
Solución:
Para descomponer en fracciones parciales a una función racional con factores lineales en el denominador, igualamos la expresión a la suma de términos fraccionarios cuyo denominador es uno de los factores lineales y numerador una constante desconocida {a}_{n} .
En nuestro caso, solo tendremos dos fracciones con dos constantes desconocidas {a}_{1} y {a}_{2} .
\frac{1}{\left(x+1\right)\left(x+2\right)}=\frac{{a}_{1}}{x+1}+\frac{{a}_{2}}{x+2}
Pasamos a multiplicar el denominador de la izquierda a la derecha.
1={a}_{1}\left(x+2\right)+{a}_{2}\left(x+1\right)
Desarrollamos y agrupamos términos semejantes:
1={a}_{1}x+2{a}_{1}+{a}_{2}x+{a}_{2}
1=\left({a}_{1}+{a}_{2}\right)x+2{a}_{1}+{a}_{2}
Igualamos los coeficientes de ambos lados:
\left\{\begin{array}{c}{a}_{1}+{a}_{2}=0\\ 2{a}_{1}+{a}_{2}=1\end{array}\right.
De la primera expresión obtenemos que:
{a}_{1}=-{a}_{2}\to 2\left(-{a}_{2}\right)+{a}_{2}=1
{a}_{2}=-1
Sustituimos en el primer despeje:
{a}_{1}=-\left(-1\right)=1
Finalmente:
\frac{1}{\left(x+1\right)\left(x+2\right)}=\frac{1}{x+1}-\frac{1}{x+2}
La respuesta correcta es el inciso c).
Reactivo 35
Calcule el resultado de la siguiente integral.
\int \left({x}^{3}+2x-1\right)dx
- {x}^{3}+{x}^{2}-x+C
- \frac{{x}^{3}}{3}-{x}^{2}+x+C
- \frac{{x}^{3}}{3}+{x}^{2}-x+C
- {x}^{2}-x+C
Solución:
Para resolver esta integral indefinida, iniciamos aplicando la propiedad de la integral de una suma:
\int \left({x}^{3}+2x-1\right)dx=\int {x}^{3}dx+2\int xdx-\int dx
Finalmente, empleamos las fórmulas de la integral de una potencia y del símbolo del diferencial.
\int {x}^{3}dx+2\int xdx-\int dx=\frac{{x}^{3}}{3}+{x}^{2}-x+C
Por lo tanto:
\int \left({x}^{3}+2x-1\right)dx=\frac{{x}^{3}}{3}+{x}^{2}-x+C
Concluimos que la respuesta correcta es el inciso c).
Reactivo 36
¿Cómo queda el integrando de la integral indefinida que se muestra a continuación, luego de aplicar fracciones parciales?
\int \frac{1}{\left(2x-3\right)\left(x-1\right)}dx
- \frac{1}{2x-3}-\frac{2}{x-1}
- \frac{2}{2x-3}-\frac{1}{x-1}
- -\frac{2}{2x-3}-\frac{1}{x-1}
- \frac{2}{2x-3}+\frac{1}{x-1}
Solución:
Debido a que los factores del denominador son lineales, la descomposición en fracciones parciales quedaría de la siguiente forma:
\frac{1}{\left(2x-3\right)\left(x-1\right)}=\frac{{a}_{o}}{2x-3}+\frac{{a}_{1}}{x-1}
Ahora, pasamos a multiplicar al miembro de la derecha a los factores del denominador de la izquierda.
1={a}_{o}\left(x-1\right)+{a}_{1}\left(2x-3\right)
Desarrollamos los productos notables y agrupamos términos semejantes.
1={a}_{o}x-{a}_{o}+2{a}_{1}x-3{a}_{1}
1=\left({a}_{o}+2{a}_{1}\right)x-{a}_{o}-3{a}_{1}
Aplicamos igualación de términos.
\left\{\begin{array}{c}{a}_{o}+2{a}_{1}=0\\ -{a}_{o}-3{a}_{1}=1\end{array}\right.
Si sumamos la primera ecuación con la segunda nos queda:
2{a}_{1}-3{a}_{1}=1\to -{a}_{1}=1
\therefore {a}_{1}=-1
Calculamos {a}_{0} sustituyendo a {a}_{1} en la primera ecuación.
{a}_{o}=-2{a}_{1}\to {a}_{o}=-2\left(-1\right)=2
Finalmente:
\begin{array}{c}{a}_{o}=2\\ {a}_{1}=-1\end{array}
Sustituyendo en la descomposición:
\frac{1}{\left(2x-3\right)\left(x-1\right)}=\frac{2}{2x-3}-\frac{1}{x-1}
Finalmente:
\int \frac{1}{\left(2x-3\right)\left(x-1\right)}dx=\int \frac{2}{2x-3}-\frac{1}{x-1}dx
La respuesta correcta al problema es el inciso b).
Reactivo 37
Hallar la integral indefinida.
\int \mathrm{ln}xdx
- \frac{2{x}^{3}}{3}-\frac{3{x}^{2}}{2}+4\mathrm{ln}\left|x\right|+C
- \frac{2{x}^{3}}{3}-\frac{3{x}^{2}}{2}-4\mathrm{ln}\left|x\right|+C
- -\frac{2{x}^{3}}{3}-\frac{3{x}^{2}}{2}+4\mathrm{ln}\left|x\right|+C
- \frac{{x}^{3}}{3}-\frac{{x}^{2}}{2}+4\mathrm{ln}\left|x\right|+C
Solución:
Para esta integral no existe una fórmula inmediata y tampoco es posible aplicar algún cambio de variables. Es necesario emplear integración por partes.
\int udv=uv-\int vdu
En este caso u=\mathrm{ln}x y dv=dx .
u=\mathrm{ln}x\to du=\frac{1}{x}dx
v=x
Reacomodamos la integral empleando integración por partes:
\int \mathrm{ln}xdx=x\mathrm{ln}x-\int x\frac{1}{x}dx=x\mathrm{ln}x-\int dx
Resolvemos la integral indicada, la cuál es inmediata.
x\mathrm{ln}x-\int dx=x\mathrm{ln}x-x+C
Finalmente:
\int \mathrm{ln}xdx=x\left(\mathrm{ln}x-1\right)+C
Concluimos que la respuesta correcta es el inciso d).
Reactivo 38
Calcule el valor de la integral definida.
i={\int }_{0}^{4}\left({x}^{2}+1\right)dx
- \frac{1}{3}
- \frac{7}{3}
- \frac{76}{3}
- -\frac{76}{3}
Solución:
Las integrales definidas se calculan aplicando el segundo teorema fundamental del cálculo.
{\int }_{a}^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right)
Donde F es la primitiva de f . Esto significa que primero integramos indefinidamente y luego se evalúa a la función resultante en los extremos. Separamos a la integral mediante la propiedad de la integral de la suma:
{\int }_{0}^{4}\left({x}^{2}+1\right)dx={\int }_{0}^{4}{x}^{2}dx+{\int }_{0}^{4}dx
Efectuamos las integrales inmediatas:
{\int }_{0}^{4}{x}^{2}dx+{\int }_{0}^{4}dx=\left.\frac{{x}^{3}}{3}\right|\begin{array}{c}4\\ \\ 0\end{array}+\left.\begin{array}{c}\\ x\\ \end{array}\right|\begin{array}{c}4\\ \\ 0\end{array}=\frac{{4}^{3}}{3}-\frac{{0}^{3}}{3}+4-0=\frac{76}{3}
Concluimos que la respuesta correcta es el inciso c).
Reactivo 39
¿Cuál es el valor de la siguiente integral definida?
i={\int }_{1}^{3}\sqrt{x}dx
- 2\sqrt{3}-\frac{2}{3}
- \sqrt{3}-\frac{2}{3}
- 2\sqrt{3}+\frac{2}{3}
- 2\sqrt{3}-\frac{1}{3}
Solución:
Integramos indefinidamente para luego aplicar el segundo teorema fundamental del cálculo.
{\int }_{1}^{3}\sqrt{x}dx={\int }_{1}^{3}{x}^{1/2}dx=\left.\frac{{x}^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right|\begin{array}{c}3\\ \\ 1\end{array}=\left.\frac{2{x}^{\frac{3}{2}}}{3}\right|\begin{array}{c}3\\ \\ 1\end{array}
Evaluando la integral nos queda:
\left.\frac{2{x}^{\frac{3}{2}}}{3}\right|\begin{array}{c}3\\ \\ 1\end{array}=\frac{2}{3}\cdot {\left(3\right)}^{\frac{3}{2}}-\frac{2}{3}\cdot {\left(1\right)}^{\frac{3}{2}}=2\cdot {3}^{\frac{1}{2}}-\frac{2}{3}=2\sqrt{3}-\frac{2}{3}\approx 2.7974
La respuesta correcta es la opción a).
Reactivo 40
Calcule el valor de la integral.
{\int }_{0}^{2\pi }\mathrm{sin}xdx
- 1
- \infty
- 0
- -1
Solución:
Para resolver esta integral, debemos aplicar el razonamiento lógico antes que los cálculos matemáticos. Recordemos que la función seno es cíclica, de tal forma que los semiciclos positivos tienen la misma forma que los semiciclos negativos.
Esto último provoca que el área de los semiciclos positivos sea positiva, mientras que para los semiciclos negativos sea negativa. Como consecuencia, el área del seno entre \left[0, \pi \right] se anula con el área desde \left[\pi , 2\pi \right] .
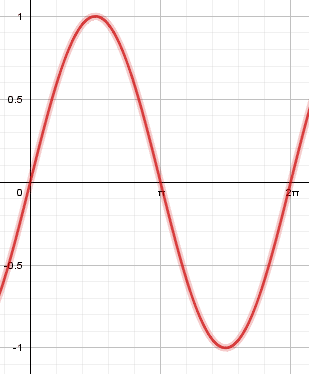
El resultado de {\int }_{0}^{2\pi }\mathrm{sin}xdx es cero.
{\int }_{0}^{2\pi }\mathrm{sin}xdx=0
La respuesta correcta es el inciso c).

