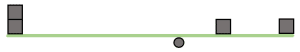¡Hola de nuevo, aspirante! Si vas a aplicar al IPN y tu carrera pertenece al área de Ingeniería y Ciencias Físico-Matemáticas, con este examen simulador podrás poner a prueba tus conocimientos en la materia de matemáticas.

Durante el simulacro de examen vamos a resolver 50 reactivos que cubren la mayoría de los temas de la guía más reciente.
Versión 2: Antes de comenzar debes saber que esta es la segunda versión del examen simulacro, para ingresar a la primera versión da clic aquí.
Vamos a dividir este examen simulacro en 5 partes, abajo encontrarás los primeros 10 reactivos, antes de comenzar échale un ojo a la siguiente información.
Estructura del Examen IPN
Lo primero que tienes que saber es que el examen del IPN abarca distintas materias, y que el examen de admisión se compone de 140 reactivos. Además de que el examen que vas a presentar es una nueva versión.
A continuación te muestro las materias y distribución de reactivos por área del conocimiento:
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
Cambios en el examen
En el examen de admisión pasado la cantidad de reactivos era igual para todas las áreas, ahora varía en función de tu carrera. Aquí tienes un resumen de los cambios más importantes.
- Competencia escrita y competencia lectora abarca los temas de español.
- La cantidad de reactivos por materia ahora depende del área de la carrera a la que apliques.
- El nuevo examen incluye inglés (Reading Comprehension) e Historia.
Para conocer todo sobre el nuevo examen de admisión al IPN puedes ingresar al siguiente artículo.
Temario Matemáticas Ing. y Cs. Físico Matemáticas
Estos son los temas de matemáticas que deberás estudiar antes de presentar el examen de ingreso:
- Razonamiento matemático.
- Álgebra.
- Geometría y trigonometría.
- Geometría analítica.
- Probabilidad y estadística.
- Cálculo diferencial
- Cálculo integral
- Probabilidad y estadística
Vamos a comenzar con los reactivos del examen simulador.
Reactivo 1
Identificar los términos faltantes que completan a la siguiente sucesión:
\frac{7}{6}, -,\frac{3}{2}, -,\frac{11}{6}, \dots
- \frac{4}{3},\frac{5}{3}
- \frac{1}{3},\frac{1}{3}
- \frac{3}{4},\frac{3}{5}
- \frac{1}{4},\frac{1}{5}
Solución:
Este problema puede ser resuelto de dos formas. La primera, a través de un sencillo sistema de ecuaciones o la segunda, estudiando cómo evoluciona la sucesión a lo largo de sus términos. En esta ocasión, lo haremos de la segunda forma.

Debido a que faltan valores de por medio en la sucesión, no podemos conocer la diferencia entre dos elementos consecutivos. Por otra parte, si podemos calcular la diferencia entre los elementos con un término de por medio. Vemos que la diferencia es constante, por tanto, la sucesión es una serie aritmética.
Como la diferencia entre elementos de por medio es igual a dos veces la diferencia entre elementos consecutivos tenemos:
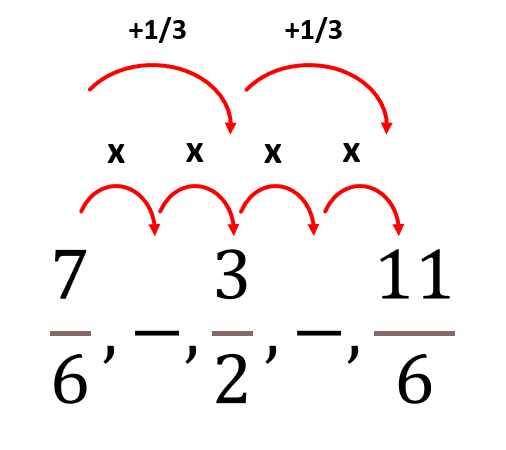
2x=\frac{1}{3}\to x=\frac{1}{6}
La diferencia entre elementos consecutivos es \frac{1}{6} .
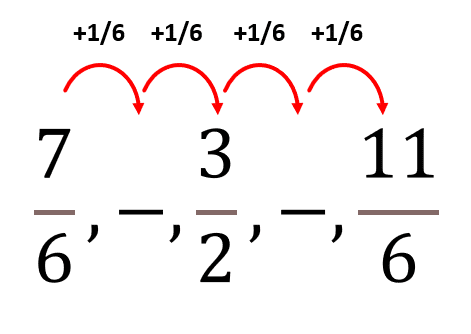
Completando la serie nos queda:
\frac{7}{6},\frac{4}{3},\frac{3}{2},\frac{5}{3},\frac{11}{6}, \dots
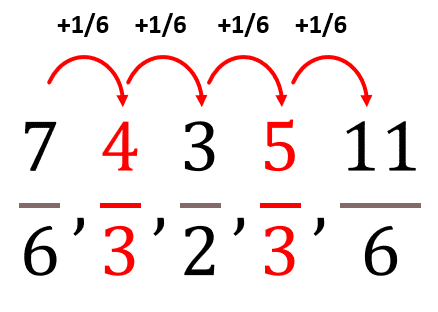
Concluimos que la respuesta correcta es el inciso a).
Reactivo 2
Indique el elemento que le da continuidad a la siguiente serie numérica:
13, 21, 31, 43, 57, \dots
- 75
- 76
- 74
- 73
Solución:
Comencemos identificando la diferencia entre elementos consecutivos.
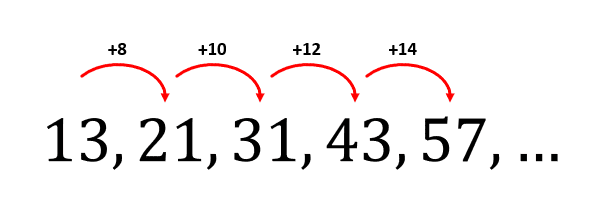
El incremento entre los términos no es constante, pero estudiando los propios incrementos, vemos que aumentan de 2 en 2.
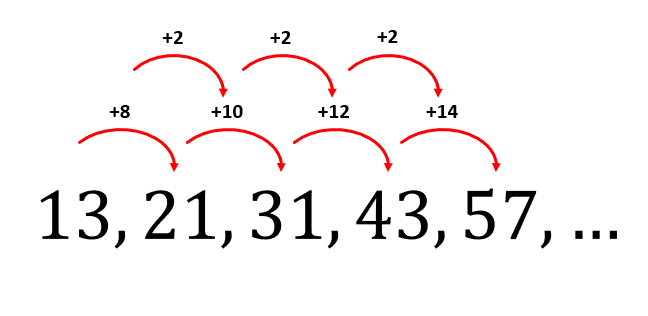
Le sumamos 2 al incremento actual para obtener el siguiente.
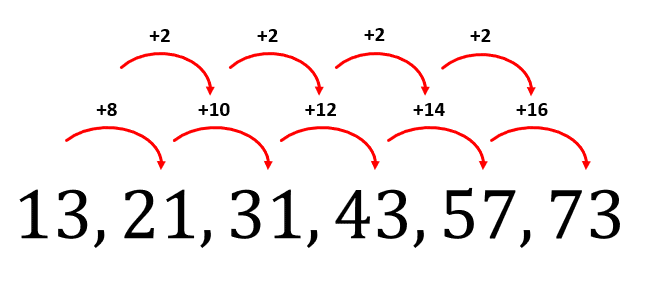
El elemento que da continuidad a la sucesión es 73. La respuesta correcta es el inciso d).
Reactivo 3
A partir de la siguiente sucesión numérica:
8, 7, 11, 10, 14, \dots
Identifique los siguientes 2 términos.
- 10 y 18
- 13 y 17
- 17 y 13
- 12 y 15
Solución:
Examinando visualmente la serie, nos damos cuenta que hay elementos que disminuyen y otros que aumentan, por lo que debemos identificar de qué forma ocurren los incrementos y decrementos.
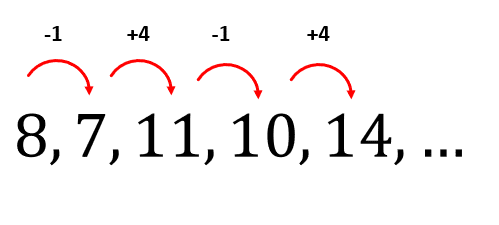
Decremento de 1 – Incremento de 4 – Decremento de 1 – Incremento de 4
Siguiendo la forma alternada de los decrementos e incrementos, el siguiente debería ser un decremento de 1 y luego un incremento de 4.
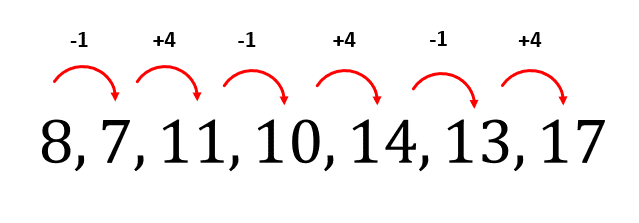
Los siguientes dos elementos de la serie son 13 y 17.
La respuesta correcta es el inciso b).
Reactivo 4
A partir de las siguientes figuras, ¿en cuál de ellas se mantiene el equilibrio?
Solución:
Aunque parezca que debemos recurrir a la física para resolver este problema, nuestro sentido común y algo de análisis espacial serán más que suficientes.
Examinando la imagen, sabemos que los cuadrados son del mismo tamaño. Por otro lado, la posición relativa entre los cuadrados y el punto de equilibrio contribuirá a que el sistema se mueva hacia algún lado.
Examinemos estos factores en la figura del inciso a.
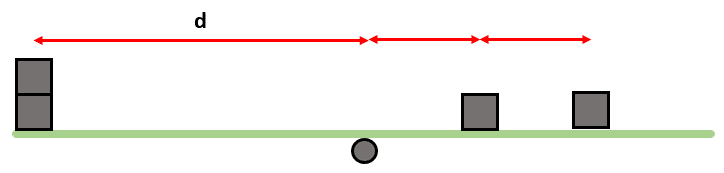
Los dos bloques puestos a una distancia d del punto de equilibrio, son compensados por los otros dos bloques colocados aproximadamente a \frac{1}{3} y \frac{2}{3} del punto. El inciso a) es la respuesta correcta. Analicemos rápidamente las otras opciones.
En el inciso b, los dos bloques apilados tienen una mayor distancia respecto al punto. No hay equilibrio.
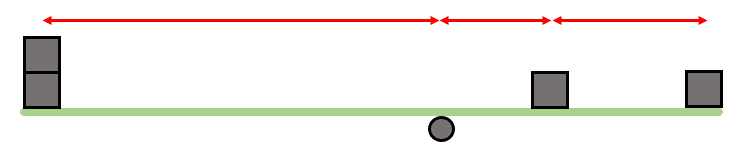
Para el inciso c, el bloque del centro no contribuye al desplazamiento de la barra. Por otro lado, del lado derecho hay dos bloques en tal disposición que superan al único bloque de la izquierda.

Una situación similar se muestra en la figura del inciso d.
Concluimos que la respuesta correcta es la opción a).
Reactivo 5
Encontrar el valor de dos números positivos, si se sabe que su diferencia es igual a 20 y que su producto es igual a \frac{3}{2} .
- x=\frac{803}{40}, y=\frac{3}{40}
- x=\frac{80}{40}, y=\frac{1}{40}
- x=\frac{3}{40}, y=\frac{3}{40}
- x=\frac{1}{40}, y=\frac{3}{40}
Solución:
Este problema se resuelve mediante un sistema de ecuaciones. Antes, debemos encontrar las expresiones descritas en lenguaje natural por el enunciado.
…si se sabe que su diferencia es igual a 20…
x-y=20
…que su producto es igual a \frac{3}{2} .
xy=\frac{3}{2}
Despejamos a x de la primera ecuación para sustituirlo en la segunda.
x=20+y\to \left(20+y\right)y=\frac{3}{3}
Desarrollamos.
{y}^{2}+20y-\frac{3}{2}=0\to 2{y}^{2}+40y-3=0
Aplicamos la fórmula de segundo grado.
y=\frac{-40\pm \sqrt{{40}^{2}-4\left(2\right)\left(-3\right)}}{2\left(2\right)}=\frac{-40\pm \sqrt{1624}}{4}
En este caso, solo tomamos la parte positiva debido a que x y y deben ser positivos.
y=\frac{-40+40.3}{4}=\frac{0.3}{4}=\frac{3}{40}
Sustituimos en la primera ecuación para obtener el valor de x .
x=20+y\to x=20+\frac{3}{40}=\frac{803}{40}
Finalmente:
x=\frac{803}{40}, y=\frac{3}{40}
La respuesta correcta es el inciso a).
Reactivo 6
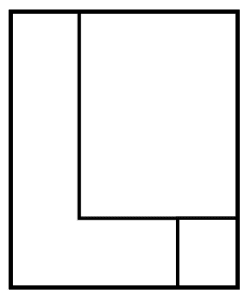
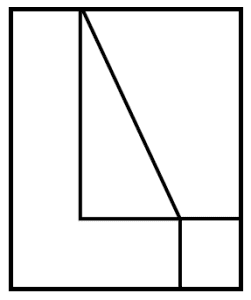
Identifique la vista de perfil, para la siguiente figura:
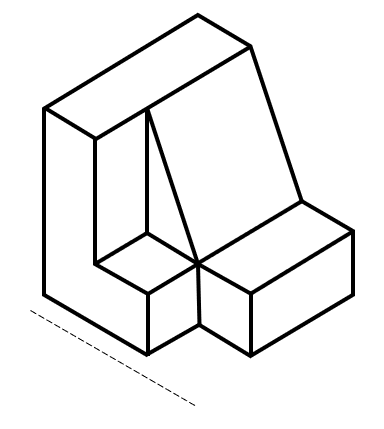
Solución:
En dibujo técnico, la vista de perfil de una figura tridimensional se obtiene mediante las proyecciones de sus aristas en un plano, con vista desde su parte frontal.
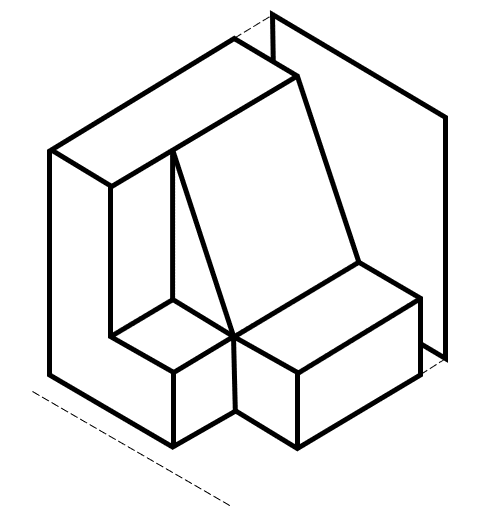
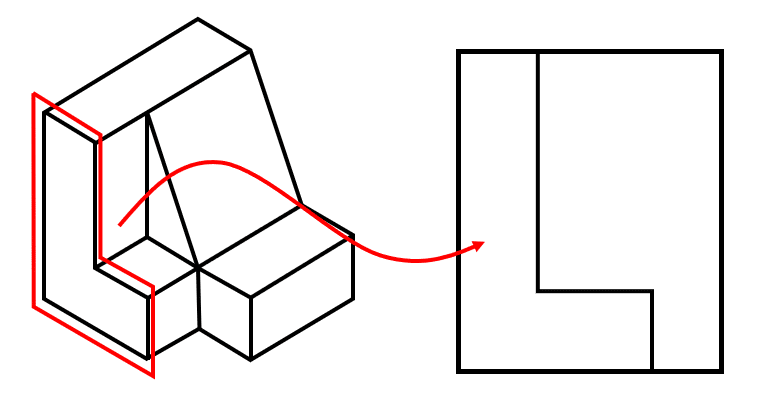
Vayamos identificando cada uno de los elementos que se proyectan en el plano. Desde la parte más frontal de la figura, se proyecta una “L”.
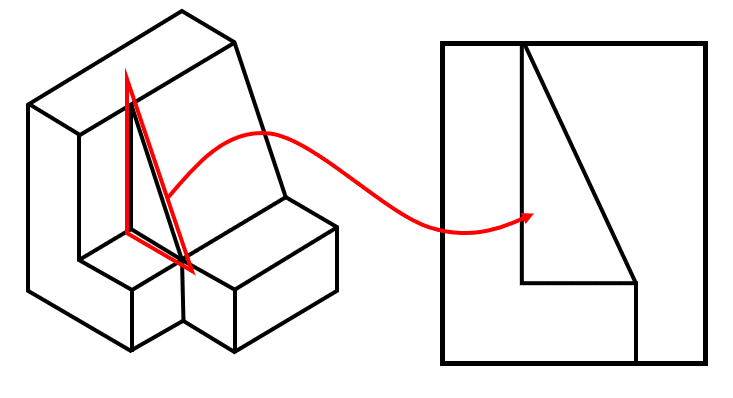
Por encima de la “L”, se proyecta un triángulo rectángulo cuya hipotenusa va desde la parte superior hasta la base de la “L”.
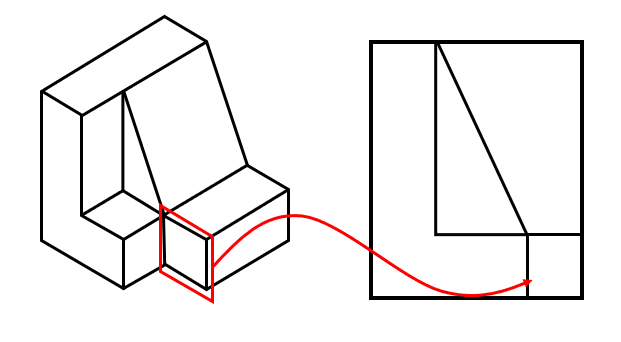
Finalmente, frente a la base de la “L” se proyecta un cuadrado.
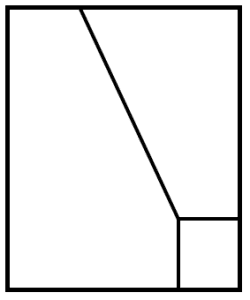
La vista de perfil de la figura es:
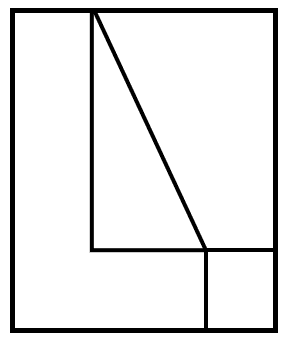
Concluimos indicando como respuesta correcta al inciso b).
Reactivo 7
La semisuma del incremento de un número más cuatro veces el número.
- \frac{x}{2}+1+4x
- \frac{x+1+4x}{2}
- \frac{x+1}{2}+4x
- x+\frac{1}{2}+4x
Solución:
Debemos transformar la relación indicada en lenguaje natural a lenguaje algebraico. Analicemos el enunciado por partes para ir transformando.
La semisuma del incremento de un número…
La semisuma se refiere a dividir por dos, lo que sigue, en este caso, el incremento de un número. Al número normalmente nos referimos como x .
\frac{x+1}{2}
…más cuatro veces el número.
A lo anterior, le sumamos el número x multiplicado por cuatro.
\frac{x+1}{2}+4x
Finalmente, seleccionamos como respuesta correcta al inciso c).
Reactivo 8
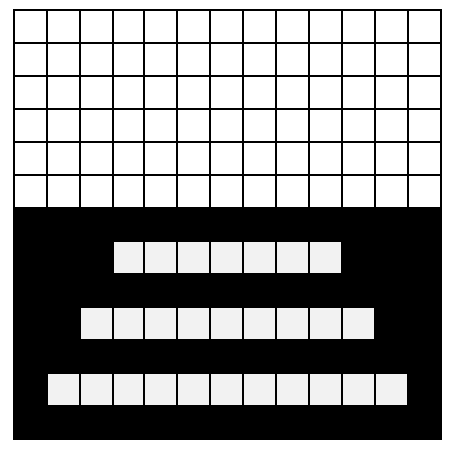
Si se continúa llenando la figura con el patrón que se muestra a continuación, ¿cuántos cuadrados negros habrá en la figura si se tienen 12×12 cuadrículas?
- 42
- 40
- 36
- 34
Solución:
En este caso, analicemos la figura para identificar la forma en que cambian los cuadros blancos.
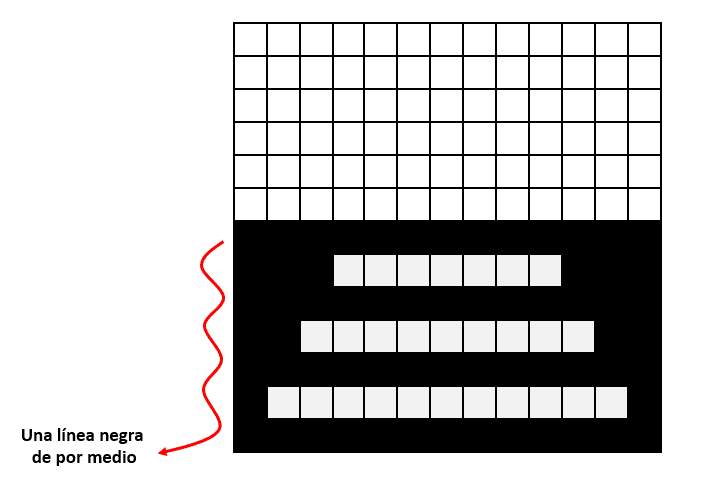
Hay una línea negra de por medio. Contando desde que inicia hasta la fila 12, habrá un total de 6 líneas negras. Por otro lado, las filas de cuadros blancos inician con 11 cuadrados y a medida que evoluciona, se acortan de 2 en 2.
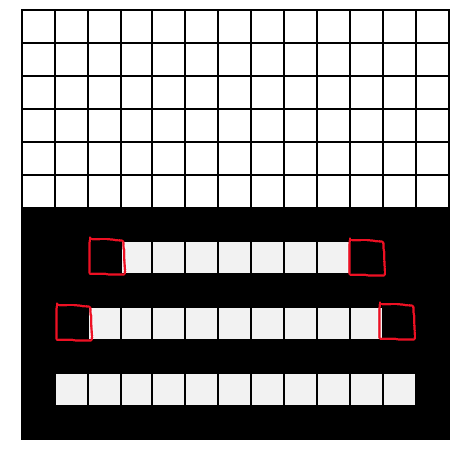
Por otra parte, al tener 6 filas negras también habrá 6 filas blancas. Contando desde la fila inferior la suma de cuadrados blancos queda:
{C}_{b}=11+9+7+5+3+1=36

Concluimos que la respuesta correcta es el inciso c).
Reactivo 9
¿Cuánto mide la diagonal de un rectángulo, si uno de sus lados mide 4 unidades y el otro es el doble que el primero?
- \sqrt{80}
- 80
- \sqrt{8}
- 2\sqrt{80}
Solución:
Para calcular la diagonal de un rectángulo, debemos aplicar el teorema de Pitágoras.
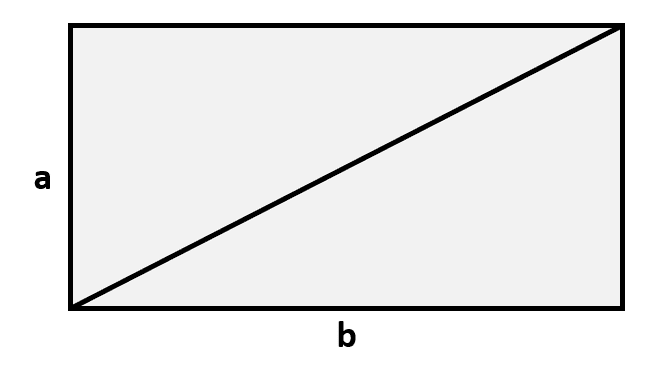
Supongamos que el lado a=4 , por consiguiente, el lado b=2a=8 . Sustituyendo en la ecuación del teorema de Pitágoras.
d=\sqrt{{a}^{2}+{b}^{2}}\to d=\sqrt{{4}^{2}+{8}^{2}}=\sqrt{80}
d\approx 8.94
Concluimos que la respuesta correcta es el inciso a).
Reactivo 10
A partir de la teoría de números, se dice que el cociente entre dos números enteros es…
- Cerrada
- Neutral
- Conmutativa
- No clausurativa
Solución:
Para el caso de los números enteros, el cociente entre dos de ellos no siempre arroja como resultado a otro entero. Por ejemplo, dividir 3÷2 da como resultado 1.5 valor que es decimal y que no pertenece a los enteros.
En este caso, se dice que la operación viola la propiedad de clausura, es decir, el resultado no pertenece al conjunto original. La división de enteros es no clausurativa. Indicamos como respuesta correcta al inciso d).