Segunda parte del examen simulador de matemáticas IPN para carreras del área de ciencias físico matemáticas. Vamos con los reactivos del 11 al 20.

Recuerda tomar notas de los ejercicios que más se te dificultan para repasar el tema después.
Reactivo 11
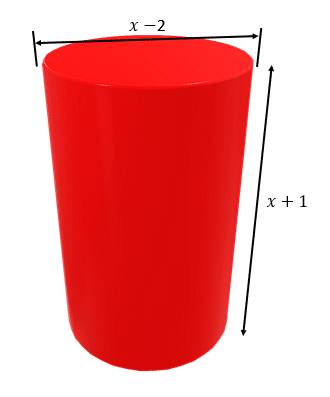
Las dimensiones de un cilindro son las que se muestran en la figura. Calcule el polinomio que representa su volumen.
- \frac{\pi }{4}\left({x}^{3}-{x}^{2}+2x+4\right)
- \frac{\pi }{4}\left({x}^{3}-2x+4\right)
- \frac{4}{\pi }\left({x}^{3}-{x}^{2}+2x+4\right)
- \frac{\pi }{4}\left({x}^{3}-{x}^{2}+4\right)
Solución:
Recordemos la ecuación para calcular el volumen de un cilindro.
{V}_{c}=\frac{\pi {D}^{2}h}{4}
Donde: D es el diámetro del cilindro y h su altura. Según la imagen tenemos que:
D=x-2, h=x+1
Sustituimos en la expresión.
{V}_{c}=\frac{\pi }{4}{\left(x-2\right)}^{2}\left(x+1\right)=\frac{\pi }{4}\left({x}^{2}-2x+4\right)\left(x+1\right)
Simplificamos.
{V}_{c}=\frac{\pi }{4}\left({x}^{3}-2{x}^{2}+4x+{x}^{2}-2x+4\right)=\frac{\pi }{4}\left({x}^{3}-{x}^{2}+2x+4\right)
Finalmente, la expresión para calcular el volumen del cilindro es:
{V}_{c}\left(x\right)=\frac{\pi }{4}\left({x}^{3}-{x}^{2}+2x+4\right)
La respuesta correcta es el inciso a).
Reactivo 12
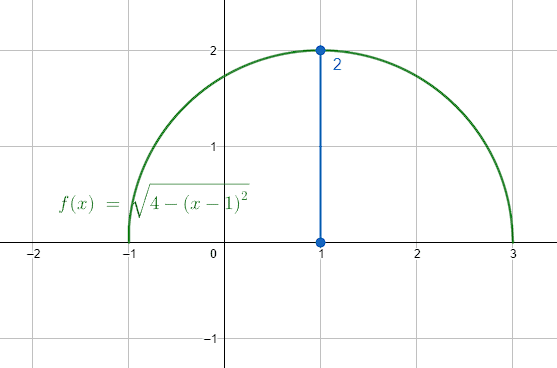
A partir de la función f\left(x\right)=\sqrt{{4-\left(x-1\right)}^{2}} , el valor ___ perteneciente a su dominio da como resultado 2.
- x=2
- x=-1
- x=-2
- x=1
Solución:
En este caso, la vía más rápida para encontrar ese valor de x , es igualando a la función a 2 para luego despejar a x .
2=\sqrt{{4-\left(x-1\right)}^{2}}
Elevamos al cuadrado de ambos lados de la igualdad y despejamos.
4=4-{\left(x-1\right)}^{2}\to {\left(x-1\right)}^{2}=0
El binomio al cuadrado se anula cuando x=1 . Concluimos que la función toma el valor de 2 cuando x=1 . La respuesta correcta es el inciso d).
Reactivo 13
Encuentre el valor de y , a partir del siguiente sistema de ecuaciones.
\begin{array}{c}x+y-z=2\\ x+y+z=4\\ 2x-y=12\end{array}
- 1
- -2
- 5
- 3
Solución:
Para resolver el sistema de ecuaciones, podemos emplear cualquier método: por igualación, sustitución, reducción o la regla de Cramer. Debido a que solo nos interesa el valor de y , los métodos por reducción y Cramer son más convenientes.
Seleccionamos la regla de Cramer como método de solución. Comenzamos calculando el determinante del sistema.
{\mathrm{\Delta }}_{\mathrm{s}}=\left|\begin{array}{ccc}1& 1& -1\\ 1& 1& 1\\ 2& -1& 0\end{array}\right|=\left|\begin{array}{cc}1& 1\\ -1& 0\end{array}\right|\left(1\right)-\left|\begin{array}{cc}1& 1\\ 2& 0\end{array}\right|\left(1\right)+\left|\begin{array}{cc}1& 1\\ 2& -1\end{array}\right|\left(-1\right)
{\mathrm{\Delta }}_{s}=\left(0+1\right)\left(1\right)-\left(0-2\right)\left(1\right)+\left(-1-2\right)\left(-1\right)=6
Ahora, calculamos el determinante de la variable y .
{\mathrm{\Delta }}_{y}=\left|\begin{array}{ccc}1& 2& -1\\ 1& 4& 1\\ 2& 12& 0\end{array}\right|=\left|\begin{array}{cc}4& 1\\ 12& 0\end{array}\right|\left(1\right)-\left|\begin{array}{cc}1& 1\\ 2& 0\end{array}\right|\left(2\right)+\left|\begin{array}{cc}1& 4\\ 2& 12\end{array}\right|\left(-1\right)
{\mathrm{\Delta }}_{y}=\left(0-12\right)\left(1\right)-\left(0-2\right)\left(2\right)+\left(12-8\right)\left(-1\right)=-12
Calculamos el valor de y como:
y=\frac{{\mathrm{\Delta }}_{y}}{{\mathrm{\Delta }}_{s}}=-\frac{12}{6}=-2
El valor de y para el sistema de ecuaciones es -2.
La respuesta correcta es el inciso b).
Reactivo 14
Desarrolle la siguiente expresión algebraica.
{\left(5{x}^{3}{y}^{3}+3\right)}^{2}
- 25{x}^{6}{y}^{6}+15{x}^{3}{y}^{3}+3
- 25{x}^{3}{y}^{3}+30{x}^{6}{y}^{6}+9
- 25{x}^{6}{y}^{6}+30{x}^{3}{y}^{3}+9
- 25{x}^{6}{y}^{6}-30{x}^{3}{y}^{3}+3
Solución:
Para desarrollar este binomio al cuadrado, empleamos el producto notable que lleva el mismo nombre.
{\left(a+b\right)}^{2}={a}^{2}+2ab+{b}^{2}
En este caso a=5{x}^{3}{y}^{3} y b=3 . Desarrollando nos queda:
{\left(5{x}^{3}{y}^{3}+3\right)}^{2}={\left(5{x}^{3}{y}^{3}\right)}^{2}+2\left(5{x}^{3}{y}^{3}\right)\left(3\right)+{3}^{2}
Resolvemos las potencias.
{\left(5{x}^{3}{y}^{3}+3\right)}^{2}=25{x}^{6}{y}^{6}+30{x}^{3}{y}^{3}+9
Comparando con los incisos, la respuesta correcta es c).
Reactivo 15
Exprese en lenguaje algebraico la ecuación que representa la siguiente relación matemática:
“El cuadrado del incremento de un número sobre el decremento del mismo número”
- \frac{{\left(x+1\right)}^{2}}{x-1}
- \frac{x+1}{x-1}
- {\left(\frac{x+1}{x-1}\right)}^{2}
- \frac{x-1}{{\left(x+1\right)}^{2}}
Solución:
Para resolver este tipo de problemas, debemos analizar cada parte de la frase para convertirla en ecuación.
El cuadrado del incremento de un número
Recordemos que “un número” hace referencia a una variable, en este caso x . El incremento es x+1 y el cuadrado indica que elevamos al binomio al cuadrado.
{\left(x+1\right)}^{2}
… sobre el decremento del mismo número.
Al binomio anterior, lo dividimos por el decremento de x , es decir, x-1 .
\frac{{\left(x+1\right)}^{2}}{x-1}
Finalmente:
“El cuadrado del incremento de un número sobre el decremento del mismo número”
\frac{{\left(x+1\right)}^{2}}{x-1}
La respuesta correcta es el inciso a).
Reactivo 16
La identidad 1+{\mathrm{tg}}^{2}x= ___, es una de las identidades trigonométricas Pitagóricas.
- \mathrm{sec}x
- {\mathrm{sec}}^{2}x
- {\mathrm{csc}}^{2}x
- {\mathrm{cot}}^{2}x
Solución:
Recordemos que la identidad pitagórica fundamental es en términos del seno y coseno.
{\mathrm{sin}}^{2}x+{\mathrm{cos}}^{2}x=1
Ahora, si dividimos la expresión por {\mathrm{cos}}^{2}x nos queda:
\frac{{\mathrm{sin}}^{2}x}{{\mathrm{cos}}^{2}x}+\frac{{\mathrm{cos}}^{2}x}{{\mathrm{cos}}^{2}x}=\frac{1}{{\mathrm{cos}}^{2}x}
{\mathrm{tan}}^{2}x+1={\mathrm{sec}}^{2}x
Por tanto, la razón trigonométrica que completa la identidad del enunciado es {\mathrm{sec}}^{2}x .
La respuesta correcta es el inciso b).
Reactivo 17
Demuestre que si dos triángulos ABC y {A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}} son semejantes, entonces sus perímetros son proporcionales.
- {S}_{ABC}={a}^{2}{S}_{{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}
- {S}_{ABC}=a{S}_{{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}
- {S}_{ABC}=a-{S}_{{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}
- {S}_{ABC}=a+{S}_{{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}
Solución:
Primero, recordemos qué significa que dos triángulos sean semejantes:
Dos o más triángulos son proporcionales, si sus ángulos correspondientes son iguales. Como consecuencia, sus lados serán proporcionales de acuerdo a una razón a .
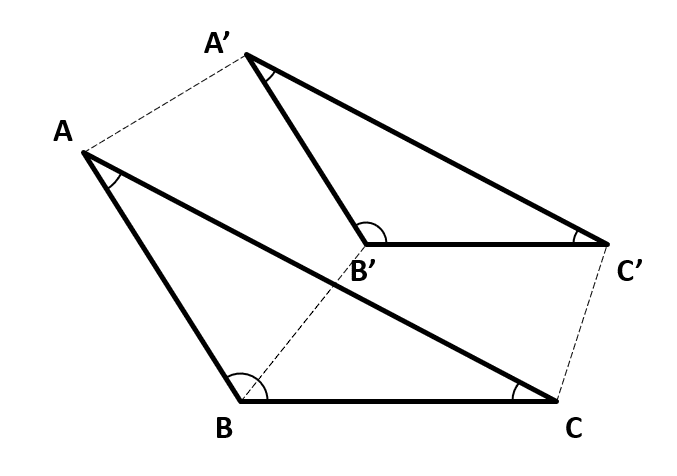
Al ser proporcionales los triángulos, podemos decir que:
\frac{AB}{{A}^{\text{'}}{B}^{\text{'}}}=\frac{BC}{{B}^{\text{'}}{C}^{\text{'}}}=\frac{CA}{{C}^{\text{'}}{A}^{\text{'}}}=a
También:
AB=a{A}^{\text{'}}{B}^{\text{'}} , BC=a{B}^{\text{'}}{C}^{\text{'}} , CA=a{C}^{\text{'}}{A}^{\text{'}}
Ahora, recordando la fórmula del perímetro:
{S}_{ABC}=AB+BC+CA , {S}_{{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}={A}^{\text{'}}{B}^{\text{'}}+{B}^{\text{'}}{C}^{\text{'}}+{C}^{\text{'}}{A}^{\text{'}}
Si sustituimos los lados ABC por los lados {A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}} , nos queda.
{S}_{ABC}=a{A}^{\text{'}}{B}^{\text{'}}+a{B}^{\text{'}}{C}^{\text{'}}+a{C}^{\text{'}}{A}^{\text{'}}=a\left({A}^{\text{'}}{B}^{\text{'}}+{B}^{\text{'}}{C}^{\text{'}}+{C}^{\text{'}}{A}^{\text{'}}\right)
Finalmente:
{S}_{ABC}=a{S}_{{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}
Si dos triángulos son semejantes, sus perímetros son proporcionales según la razón a .
La respuesta correcta es el inciso b).
Reactivo 18
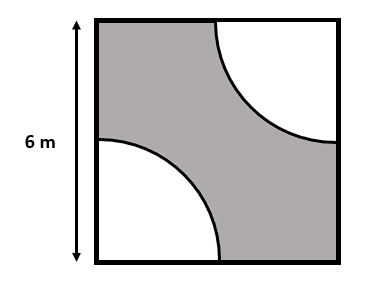
Calcule el área sombreada de la figura que se muestra a continuación:
- 36-9\pi
- 16-\frac{9}{2}\pi
- 36-\frac{9}{2}\pi
- 36+\frac{9}{2}\pi
Solución:
Para obtener el área sombreada (de color gris), calculamos por separado el área del cuadrado y los dos sectores circulares, para luego restarlos. Escrito de forma matemática quedaría:
{A}_{s}={A}_{c}-{A}_{sc1}-{A}_{sc2}
Calculando el área del cuadrado:
{A}_{c}=6\cdot 6=36 {u}^{2}
Para el sector circular, vemos que se trata de dos cuartos de circunferencia que juntos suman media circunferencia. El área entonces es la de medio círculo.
{A}_{sc}=\frac{\pi {r}^{2}}{2}
El radio es igual a medio lado del cuadrado, es decir 3 unidades.
{A}_{sc}=\frac{\pi {3}^{2}}{2}=\frac{9}{2}\pi {u}^{2}
Calculando el área sombreada nos queda:
{A}_{s}=36-\frac{9}{2}\pi
Comparando con los incisos, concluimos que la respuesta correcta es c).
Reactivo 19
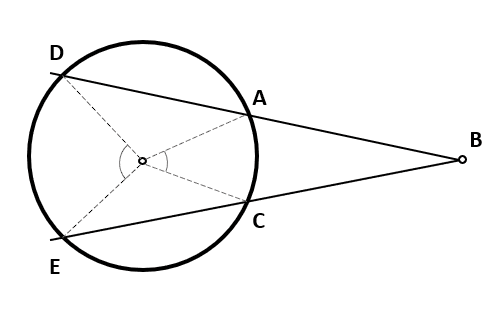
Teniendo en cuenta que los arcos DE y AC tienen una amplitud de 200° y 40°, calcule el ángulo ABC .
- 50°
- 60°
- 70°
- 80°
Solución:
Para responder esta pregunta, debemos tener muy presente cómo se calculan los ángulos notables dentro de una circunferencia. El caso que se muestra en la figura corresponde al ángulo exterior y la fórmula para calcularlo es la siguiente:
ABC=\frac{DE-AC}{2}
Donde DE y AC son las amplitudes de los arcos mayor y menor en grados. El enunciado indica que dichos arcos valen 200° y 40° respectivamente, sustituyendo en la expresión nos queda:
ABC=\frac{200-40}{2}=\frac{160}{2}=80°
La amplitud del arco ABC es de 80°.
Concluimos indicando como respuesta correcta al inciso d).
Reactivo 20
El profesor de matemáticas les ha impuesto un reto a sus estudiantes y solo pueden emplear una cinta métrica de 1 metro. Deben calcular la altura del edificio más alto de la escuela. A las 4:30 pm la sombra del edificio mide 1.5 metros, mientras que la sombra de uno de los estudiantes mide 60 cm. Si la altura del estudiante es de 1.7 metros, ¿cuál es la altura del edificio?
- 5.25 \mathrm{m}
- 4.25 \mathrm{m}
- 3.25 \mathrm{m}
- 1.25 \mathrm{m}
Solución:
Comencemos haciendo un dibujo de la situación planteada.
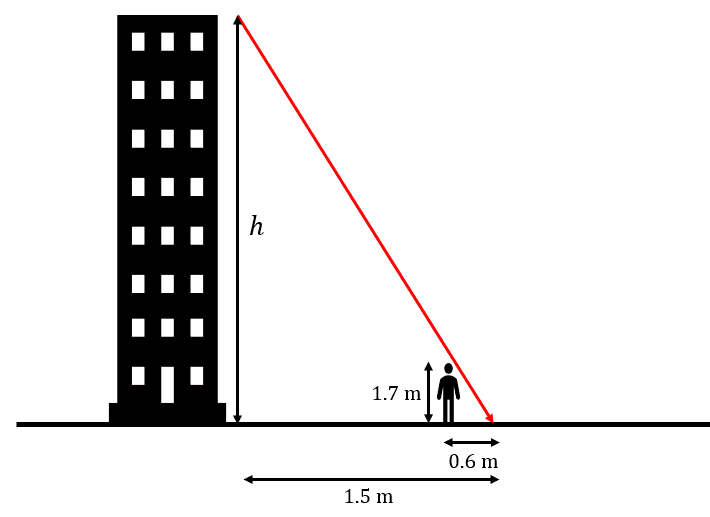
Debido a que la sombra del edificio y del estudiante se proyectan con el mismo ángulo, los triángulos que se forman son semejantes, por tanto, sus lados son proporcionales.
\frac{h}{1.5}=\frac{1.7}{0.6}
Despejamos la altura del edificio.
h=\left(\frac{1.7}{0.6}\right)\left(1.5\right)=4.25 \mathrm{m}
El edificio tiene una altura de 4.25 metros.
La respuesta correcta es el inciso b).

