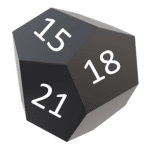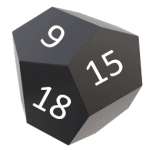¡Hola de nuevo aspirante! En este examen simulador vamos a poner a prueba tus conocimientos resolviendo 50 ejercicios de Matemáticas para el área de Ingeniería y Ciencias Físico Matemáticas del Instituto Politécnico Nacional.

Lista de ingenierías del IPN
Si no sabes si tu carrera pertenece a esta área, aquí tienes la lista completa de carreras del área de ingeniería y ciencias físico matemáticas:
- Ingeniería Aeronáutica
- Ingeniería Ambiental
- Ingeniería Biomédica
- Ingeniería Biónica
- Ingeniería Bioquímica
- Ingeniería Biotecnológica
- Ingeniería Civil
- Ingeniería Eléctrica
- Ingeniería en Alimentos
- Ingeniería en Computación
- Ingeniería en Comunicaciones y Electrónica
- Ingeniería en Control y Automatización
- Ingeniería en Energía
- Ingeniería en Informática
- Ingeniería en Inteligencia Artificial
- Ingeniería en Metalurgia y Materiales
- Ingeniería en Movilidad Urbana
- Ingeniería en Negocios Energéticos Sustentables
- Ingeniería en Robótica Industrial
- Ingeniería en Sistemas Ambientales
- Ingeniería en Sistemas Automotrices
- Ingeniería en Sistemas Computacionales
- Ingeniería en Sistemas Energéticos y Redes Inteligentes
- Ingeniería en Transporte
- Ingeniería Farmacéutica
- Ingeniería Ferroviaria
- Ingeniería Fotónica
- Ingeniería Geofísica
- Ingeniería Geológica
- Ingeniería Industrial
- Ingeniería Matemática
- Ingeniería Mecánica
- Ingeniería Mecatrónica
- Ingeniería Metalúrgica
- Ingeniería Petrolera
- Ingeniería Química Industrial
- Ingeniería Química Petrolera
- Ingeniería Telemática
- Ingeniería Textil
- Ingeniería Topográfica y Fotogramétrica
- Ingeniero Arquitecto
- Licenciatura en Ciencia de Datos
- Licenciatura en Ciencias de la Informática
- Licenciatura en Física y Matemáticas
- Licenciatura en Matemática Algorítmica
Estructura Examen IPN
La prueba de ingreso al Politécnico Nacional está dividida en dos grandes bloques: conocimientos generales y conocimientos experimentales.
- Conocimientos generales: tiene reactivos de Matemáticas, español, inglés e historia.
- Conocimientos experimentales, se compone ejercicios de química, física y biología.
En las ediciones anteriores, la cantidad de reactivos era igual, ahora varía en función de tu carrera.
A continuación te dejo los cambios del nuevo examen:
- Competencia escrita y competencia lectora, anteriormente conocida como producción escrita y comprensión de textos.
- Cantidad de reactivos variable: la cantidad de reactivos ahora depende del área de la carrera.
- Nuevas materias: se han agregado preguntas de Reading Comprehension (inglés) e Historia.
- Más reactivos por responder: El examen para todas las carreras tendrá 140 reactivos, antes eran 130 reactivos.
A continuación, te dejo una tabla que resume la estructura del examen.
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
Temario Matemáticas IyCFM
Esta lista contiene los temas de matemáticas que debes dominar antes de presentar:
- Razonamiento matemático.
- Álgebra.
- Geometría y trigonometría.
- Geometría analítica.
- Probabilidad y estadística.
- Cálculo diferencial
- Cálculo integral.
¿Cómo resolver el simulacro?
Este conjunto de problemas está diseñado para ayudarte a practicar y a mejorar la velocidad de resolución para el examen real.
Te recomiendo resolver las preguntas del simulacro por tu cuenta antes de consultar la respuesta y procedimiento, asignando un máximo de 15 minutos por cada 10 preguntas.
Guarda unos minutos finales para revisar tus respuestas, y si te encuentras con un problema difícil, resuélvelo al final.
Reactivo 1
Determine el número que completa la sucesión.
\frac{3}{4},\frac{13}{12}, -,\frac{7}{4},\frac{25}{12},\frac{29}{12}, \dots
- \frac{17}{13}
- \frac{17}{14}
- \frac{17}{18}
- \frac{17}{12}
Solución:
Para resolver cualquier sucesión numérica, debemos identificar si se trata de una serie aritmética o de una serie geométrica. La forma sencilla de hacerlo, es restar entre sí tres números sucesivos, es decir, {a}_{2}-{a}_{1} y {a}_{3}-{a}_{2} ; si la diferencia es igual, entonces se trata de una serie aritmética.
Probamos en este caso con {a}_{4}=\frac{7}{4} , {a}_{5}=\frac{25}{12} y {a}_{6}=\frac{29}{12} .
{a}_{5}-{a}_{4}=\frac{25}{12}-\frac{7}{4}=\frac{1}{3}
{a}_{6}-{a}_{5}=\frac{29}{12}-\frac{25}{12}=\frac{1}{3}
La diferencia es constante d=\frac{1}{3} , por tanto, se trata de una serie aritmética.
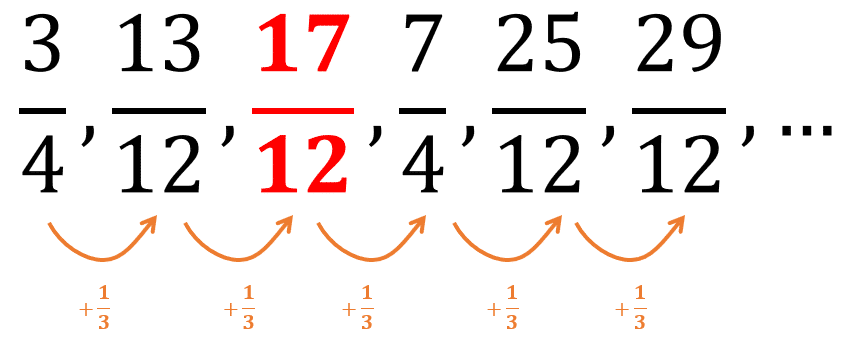
Si le sumamos \frac{1}{3} al elemento \frac{13}{12} , obtenemos al término faltante.
{a}_{3}=\frac{13}{12}+\frac{1}{13}=\frac{17}{12}
Comparando con las opciones, concluimos que la respuesta correcta es la d).
Reactivo 2
Dados los siguientes números, ¿cuál es el que tiene el mayor número de divisores?
- 16
- 18
- 22
- 26
Solución:
Para encontrar los divisores de un número, primero debemos descomponerlo en sus factores. Este procedimiento debemos aplicarlo para cada uno de los números en los incisos.
Divisores del 16.
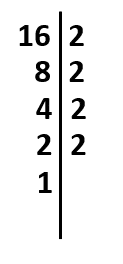
Tiene como divisores al: 1, 2, 4, 8 y 16, 5 divisores en total.
Divisores del 18.
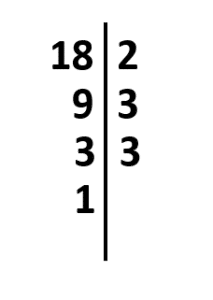
Tiene como divisores al: 1, 2, 3, 6, 9 y 18, 6 divisores en total.
Divisores del 22.
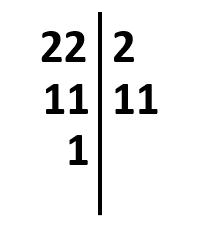
Tiene como divisores al: 1, 2, 11 y 22, 4 divisores en total.
Divisores del 26.
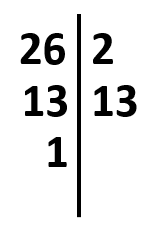
Tiene como divisores al: 1, 2, 13 y 26, 4 divisores en total.
Comparando entre sí el número de divisores de las cifras indicadas, concluimos que la de mayor cantidad de divisores es el 18. Indicamos como respuesta correcta al inciso b).
Reactivo 3
Determine el valor de x para la siguiente expresión.
{\mathrm{log}}_{2}\left(3x+4\right)-1={\mathrm{log}}_{2}\left(x+1\right)
- x=-1
- x=-2
- x=2
- x=0
Solución:
Para resolver esta ecuación logarítmica, tenemos que emplear las propiedades de los logaritmos para eliminarlo y, de esta forma, trabajar con una ecuación lineal de la que podamos despejar un valor para x .
Comenzamos pasando el 1 a la derecha y el término con logaritmo a la izquierda.
{\mathrm{log}}_{2}\left(3x+4\right)-{\mathrm{log}}_{2}\left(x+1\right)=1
Aplicamos la propiedad de la diferencia de logaritmos de igual base.
{\mathrm{log}}_{2}\left(\frac{3x+4}{x+1}\right)=1
Elevamos a la base del logaritmo en ambos miembros, es decir, elevamos a 2.
{2}^{{\mathrm{log}}_{2}\left(\frac{3x+4}{x+1}\right)}={2}^{1}\to \frac{3x+4}{x+1}=2
Teniendo una ecuación lineal, podemos despejar el valor de x que cumple con la igualdad.
3x+4=2x+2\to x=-2
Comprobamos nuestro resultado sustituyendo en la ecuación original.
{\mathrm{log}}_{2}\left(\frac{3\left(-2\right)+4}{-2+1}\right)=1\to {\mathrm{log}}_{2}\left(\frac{-2}{-1}\right)=1
{\mathrm{log}}_{2}\left(2\right)=1\to 1=1
Se cumple la igualdad. Recordemos que el logaritmo de la base es igual a 1.
Concluimos el ejercicio seleccionando como respuesta correcta la b).
Reactivo 4
Identifique la figura que completa la secuencia numérica en la figura.

Solución:
Para resolver cualquier problema que involucre a una serie gráfica, lo primero que debemos hacer es identificar los elementos que varían o cambian de figura a figura. En este caso, el objeto tridimensional permanece constante, quienes cambian son las cantidades que se muestran en sus caras.
La primera figura nos muestra 6, 9 y 12; la siguiente 9, 12 y 15. Lo que podemos identificar en estas dos secuencias es que: los números son múltiplos de 3 y que la siguiente secuencia comienza con el segundo elemento de la anterior y se agrega como último elemento el siguiente múltiplo de 3.
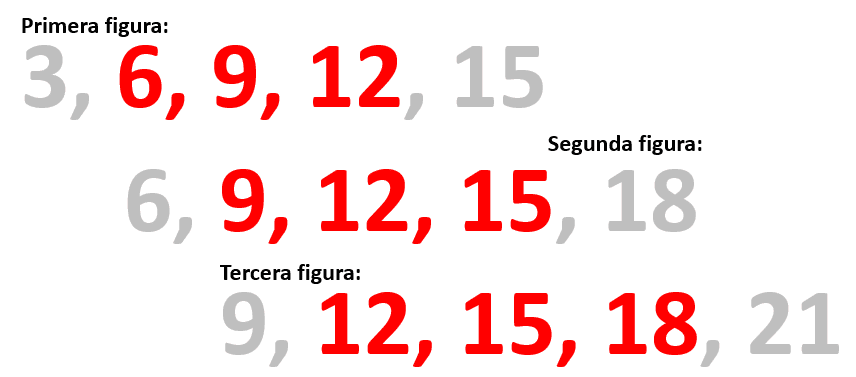
Teniendo en cuenta esto, concluimos que la siguiente figura es:
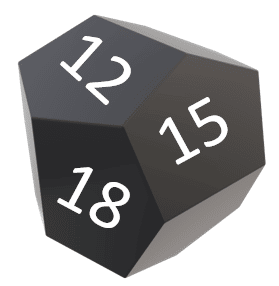
Seleccionamos como respuesta correcta al inciso a).
Reactivo 5
Identifique el número de triángulos que se visualizan en la siguiente figura.
- 5
- 6
- 7
- 8
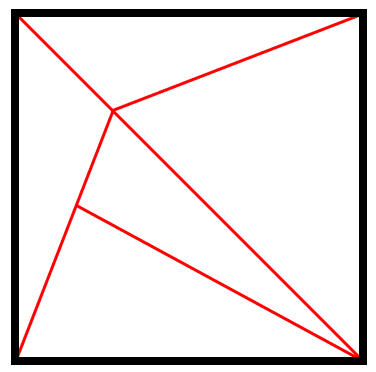
Solución:
Este tipo de problemas trata que utilices tu lógica espacial para encontrar determinada característica en la figura, para nuestro caso, el total de triángulos. Comencemos por identificar los triángulos más evidentes.
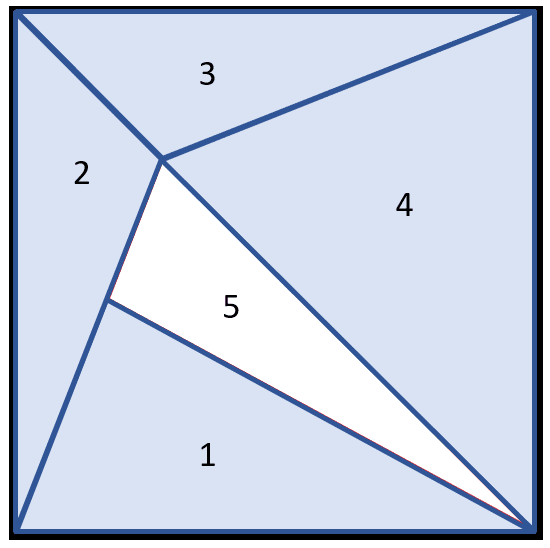
Tenemos 5 triángulos principales. Además, si juntamos a los triángulos 1 y 5 se forma un sexto, si juntamos al 3 y al 4 se forma un séptimo triángulo y al juntar 1, 2 y 5 obtenemos un octavo triángulo.
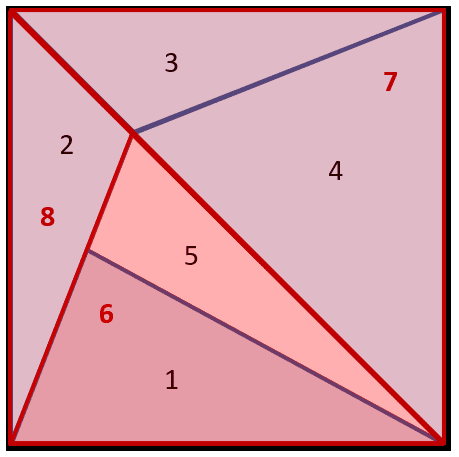
Concluimos entonces que la figura tiene un total de8 triángulos en su interior. Comparando con las opciones, seleccionamos la d) como correcta.
Reactivo 6
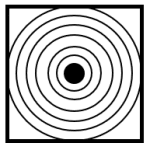
Identifique la figura que completa la siguiente serie gráfica.

Solución:
Para identificar la siguiente figura en la serie gráfica, es necesario determinar el elemento que cambia entre figuras y la ley que sigue para realizar dicho cambio. A simple vista nos damos cuenta que el círculo del centro y el contorno rectangular permanecen constantes en forma y color.
Por el contrario, la trama interior que se forma alrededor del círculo es el que cambia, básicamente aumenta en 1 arista. Primero son líneas diagonales, luego triángulos, luego son cuadrados y, siguiendo esta misma lógica, la siguiente debería tener pentágonos concéntricos al círculo.

Esto último lo encontramos en la figura del inciso b).
Concluimos entonces indicando como respuesta correcta al inciso b).
Reactivo 7
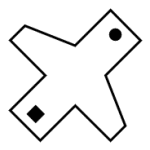
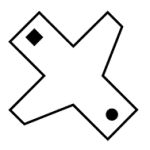
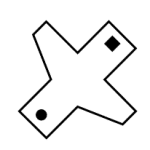
Indique la figura que se obtiene al realizar los dobleces marcados con las líneas segmentadas y luego girar la figura 45° en sentido horario.
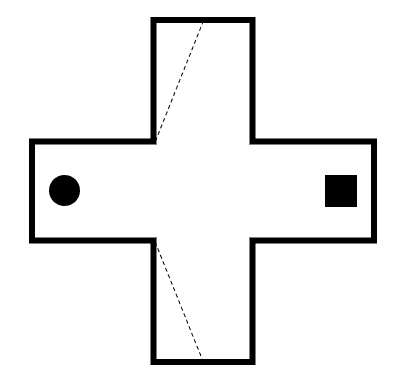
Solución:
En este caso, primero vamos a encontrar la forma de la figura luego de realizar los dobleces y posteriormente la vamos a rotar los 45° que indica el enunciado. Comenzamos por realizar los dobleces.
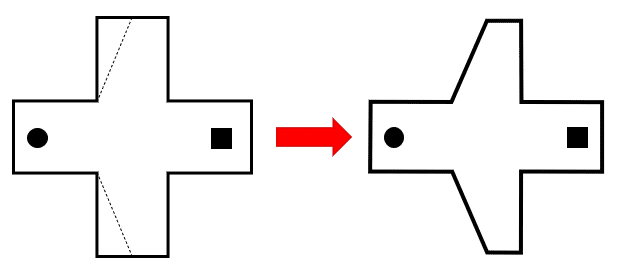
Ahora, procedemos a girar la figura 45° en sentido horario.
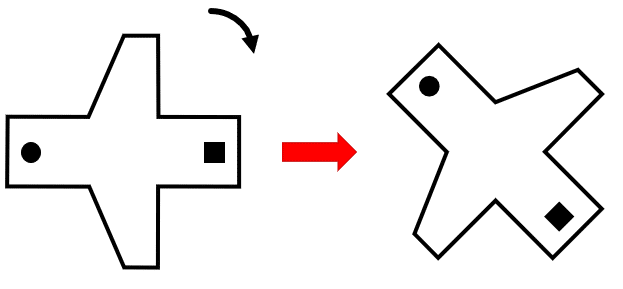
Comparando con los incisos, concluimos que la respuesta correcta se encuentra en a).
Reactivo 8
A partir de la siguiente sucesión numérica 3,\frac{11}{3},\frac{13}{3}, 5, \dots identifique cuáles serían los elementos 20 y 21.
- \frac{47}{3},\frac{49}{3}
- \frac{49}{3},\frac{47}{3}
- \frac{47}{6},\frac{49}{6}
- 47, 49
Solución:
En este caso, la forma más conveniente de encontrar los términos 20 y 21 es a partir del término general de la sucesión (la cuál, claramente es aritmética). En caso contrario, tendríamos que realizar muchas sumas sucesivas y, teniendo en cuenta el tiempo para el examen, no es la mejor opción.
Recordemos la fórmula del término general.
{a}_{n}={a}_{1}+d\left(n-1\right) \forall n\ge 1
Examinando la sucesión, sabemos que {a}_{1}=3 y que la diferencia d se calcula restando dos términos consecutivos.
d={a}_{2}-{a}_{1}=\frac{11}{3}-3=\frac{2}{3}
Finalmente:
{a}_{n}=3+\frac{2}{3}\left(n-1\right)
Sustituyendo 20 y 21 obtenemos:
{a}_{20}=3+\frac{2}{3}\left(20-1\right)=\frac{47}{3}
{a}_{21}=3+\frac{2}{3}\left(21-1\right)=\frac{49}{3}
Comparando con los incisos, concluimos que la opción a) es la respuesta correcta.
Reactivo 9
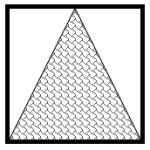
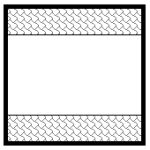
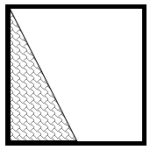
Identifique cuál de las siguientes figuras tiene mayor área sombreada.
Solución:
En este caso, no tenemos información de las dimensiones del cuadrado, por lo que debemos estimar “a ojo” qué regiones sombreadas dentro de cada figura ocupa mayor área.
Empezamos por el inciso a.
Para este cuadrado, el triángulo interno es equivalente a dos triángulos rectángulos juntos que, si los juntamos por sus hipotenusas, forman medio cuadrado.
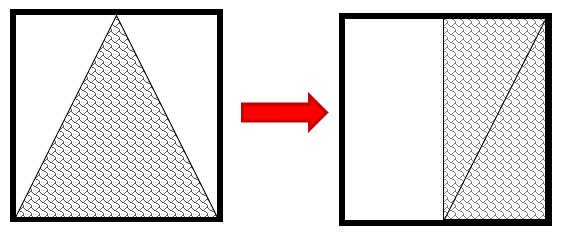
Inciso b.
Acá podemos juntar ambas franjas rectangulares para determinar si alcanzan o no a la mitad del cuadrado, de no ser así, la figura con mayor área sombreada seguiría siendo la a).
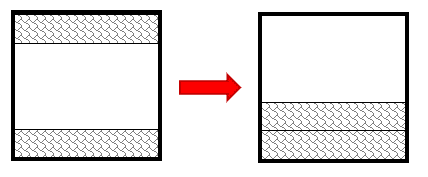
La figura a continúa teniendo mayor área.
Inciso c.
Podemos invertir uno de los triángulos y unirlo con el que se ha quedado en su posición inicial. Debemos verificar si el resultado ocupa mayor área que la figura a.
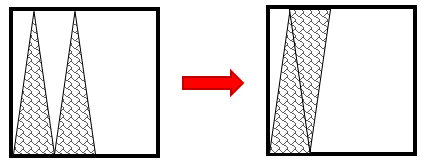
La figura a continúa teniendo mayor área.
Inciso d.
Este triángulo es el equivalente a la cuarta parte del área del cuadrado. Concluimos que la figura con mayor área sombreada es la a).
Reactivo 10
Identifique el término siguiente de la sucesión.
2, 7, 12, 17, 22, \dots
- 28
- 29
- 27
- 26
Solución:
Para encontrar el siguiente elemento de la sucesión, debemos identificar si se trata de una sucesión aritmética o geométrica. Si al término 1 le sumamos 5 obtenemos 7, el cuál es el término siguiente, si ahora le sumamos 5 nuevamente, obtenemos 12, el cuál es el término 3.
Una vez conocida la forma en la que incrementan los números de la sucesión, sólo queda sumarle al último elemento 5 para obtener al siguiente:
{a}_{6}=22+5=27
Comparando con las opciones, indicamos como correcta la d).