Vamos con la segunda parte del examen simulador de matemáticas para todas aquellas carreras que pertenecen al área de ingenierías y ciencias físico matemáticas. Para esta segunda parte del examen vamos a resolver los reactivos del 11 al 20.

Recuerda planificar tus horas de estudios, y sobre todo tomar en cuenta que matemáticas es solo una de las materias que te vas a encontrar en el examen.
Reactivo 11
Determine el valor de \mathrm{sin}\theta si se sabe que \mathrm{cos}\theta =\frac{1}{3} .
- \frac{\sqrt{8}}{3}
- \frac{\sqrt{8}}{2}
- \frac{\sqrt{8}}{5}
- \frac{\sqrt{10}}{3}
Solución:
Para resolver estos problemas, donde nos piden hallar el valor numérico de alguna de las identidades trigonométricas, podemos seguir dos caminos: armar un triángulo rectángulo con los datos disponibles o aplicar simplificación trigonométrica.
Esto último puede resultar complicado y tardío durante un examen, por tanto, te recomiendo siempre emplear la primera alternativa. Sabemos que el coseno del ángulo es igual a cociente entre el cateto adyacente y la hipotenusa, por tanto:
\mathrm{cos}\theta =\frac{1}{3}=\frac{CA}{H}
De aquí obtenemos: CA=1 , H=3 . Establecemos nuestro triángulo rectángulo:
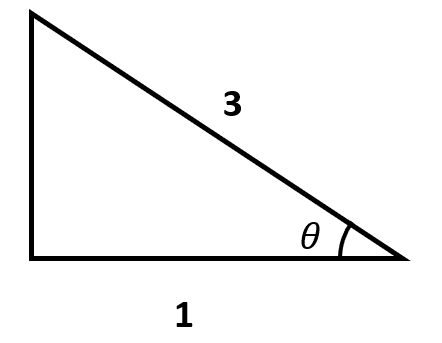
Aplicando el teorema de Pitágoras obtenemos el valor del cateto opuesto para calcular luego el seno de theta.
CO=\sqrt{{3}^{2}-{1}^{2}}=\sqrt{9-1}=\sqrt{8}
El seno de theta es igual a:
\mathrm{sin}\theta =\frac{\sqrt{8}}{3}
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 12
Si la intersección entre dos rectas da como resultado infinitos puntos, significa que son…
- Paralelas
- Oblicuas
- Equivalentes
- Perpendiculares
Solución:
El análisis del enunciado lo podemos realizar de forma geométrica o de forma netamente algebraica. Cuando decimos que dos rectas son equivalentes, si los resultados que se obtienen al sustituir valores de x en ambas rectas, se obtienen los mismos resultados para y en ambas.
Desde un punto de vista geométrico, esto significa que todos los puntos de una recta pertenecen también a la otra. Por esta razón, si intersectamos dos rectas equivalentes, el resultado serán infinitas soluciones porque ambas pasan por los mismos puntos.
Si la intersección entre dos rectas da como resultado infinitos puntos, significa que son equivalentes.
Teniendo en cuenta esto último, concluimos indicando como correcta la opción c).
Reactivo 13
¿Cuáles son las dimensiones de un rectángulo, si su base mide dos veces la altura incrementada en dos y su perímetro es de 12 unidades?
- Base 4/3, altura 14/3
- Base 4/3, altura 4/3
- Base 1/3, altura 4/3
- Base 2/3, altura 7/3
Solución:
Para encontrar las dimensiones del rectángulo, primero tenemos que convertir en lenguaje matemático las relaciones que nos da el enunciado entre su base y su altura, luego formar un sistema de ecuaciones. La primera relación nos dice:
… su base mide dos veces la altura incrementada en dos…
b=2a+2
Además, nos dice que su perímetro mide 12 unidades. Esto se puede escribir como:
12=2b+2a
Con estas dos ecuaciones, obtenemos el siguiente SEL:
\left\{\begin{array}{c}2a-b=-2\\ 2a+2b=12\end{array}\right.
Para encontrar la solución al SEL puedes emplear cualquier método que conozcas, en este caso es conveniente utilizar reducción. Multiplicamos la primera ecuación por 2 y luego la sumamos con la segunda.
2I+II:
\begin{array}{c}4a-2b=-4\\ 2a+2b=12\\ 6a=8\end{array}
Despejamos la a :
a=\frac{4}{3}
Encontramos a b sustituyendo a en la primera ecuación.
b=2\left(\frac{4}{3}\right)+2=\frac{14}{3}
Comparando con las opciones, escogemos como respuesta correcta al inciso a).
Reactivo 14
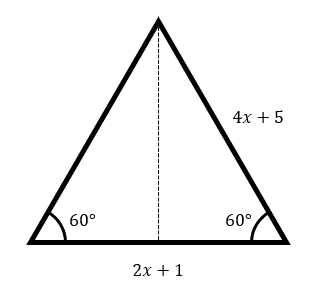
¿Cuál es la expresión que representa el área de la figura?
- \frac{1}{4}\left(2x+1\right)\left(4x+5\right)
- \frac{3}{4}\left(2x+1\right)\left(4x+5\right)
- \frac{\sqrt{2}}{4}\left(2x+1\right)\left(4x+5\right)
- \frac{\sqrt{3}}{4}\left(2x+1\right)\left(4x+5\right)
Solución:
En este caso, el enunciado solo nos pide obtener la expresión para calcular el área, por tanto, debemos encontrar las respectivas ecuaciones que representan a las variables del área de un triángulo, en este caso serían: base y altura.
{A}_{t}=\frac{ab}{2}
La base se obtiene directamente al examinar la figura:
b=2x+1
Por otro lado, la altura podemos calcular aplicando la identidad del seno o de la tangente. Esta vez emplearemos el seno.
\mathrm{sin}60°=\frac{a}{4x+5}
Vemos que la hipotenusa es uno de los lados oblicuos y la altura el segmento de trazo discontinuo.
a=\mathrm{sin}60°\left(4x+5\right)=\frac{\sqrt{3}}{2}\left(4x+5\right)
Ahora, podemos sustituir en la ecuación de área:
{A}_{t}=\frac{\frac{\sqrt{3}}{2}\left(2x+1\right)\left(4x+5\right)}{2}=\frac{\sqrt{3}}{4}\left(2x+1\right)\left(4x+5\right)
Comparando con las opciones, concluimos que la correcta es la d).
Reactivo 15
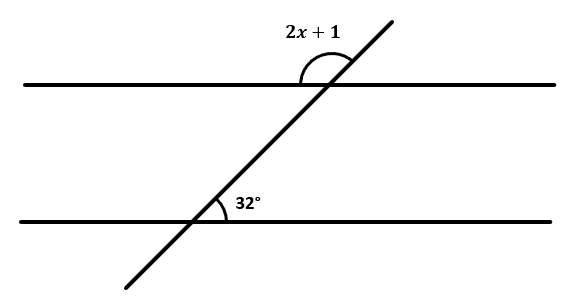
Determinar el valor del ángulo x , a partir de la siguiente figura.
- 90°
- 147°
- 127°
- 5°
Solución:
Para resolver este problema, es necesario aplicar las relaciones de ángulos por rectas paralelas y de ángulos suplementarios (que suman 180°). Comenzamos por indicar que, por paralelismo entre las rectas horizontales, el ángulo de 32° se repite para la recta superior.
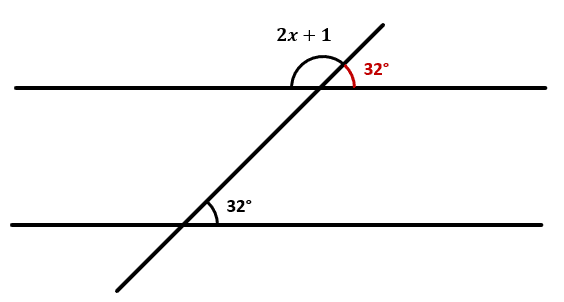
Ahora, aplicamos ángulos suplementarios.
2x+1+32=180°
Despejamos la x .
2x=180°-33
x=73.5°
Comparando con las opciones, indicamos como correcta la d).
Reactivo 16
El grado absoluto de un polinomio de __________ es igual a la mayor suma de los ___________.
- Una variable – términos
- Varias variables – exponentes
- Varias variables – términos
- Una variable – exponentes
Solución:
Según los temas referentes a polinomios se entiende por grado de un polinomio a:
- El exponente mayor entre sus términos en el caso de tener una sola variable
- La mayor suma de los exponentes de alguno de sus términos
Teniendo en cuenta esto, la frase incompleta del enunciado hace referencia al caso de un polinomio de varias variables. El inciso que completa de forma correcta es el b).
El grado absoluto de un polinomio de varias variables es igual a la mayor suma de los exponentes.
Reactivo 17
Determine el valor de x que cumple la siguiente igualdad.
\frac{1}{2x+1}=x+1
- 0 y -3/2
- 0
- 3/2
- 0 y 3/2
Solución:
Para resolver la ecuación, comenzamos por linealizar la ecuación multiplicando en ambos lados por el denominador 2x+1 .
1=\left(x+1\right)\left(2x+1\right)
Desarrollamos el producto de binomios.
2{x}^{2}+3x+1=1
Paramos el 1 al miembro de la izquierda para dejar la expresión igualada a cero.
2{x}^{2}+3x=0
Extraemos factor común x .
x\left(2x+3\right)=0
En este caso no es necesario aplicar la ecuación de segundo grado, ya que con esta sencilla factorización sabemos cuáles son los valore de x que anulan la expresión:
{x}_{1}=0
2x+3=0\to {x}_{2}=-\frac{3}{2}
Los valores de x que cumplen con la igualdad son x=0 y x=-\frac{3}{2} .
Comparando con las opciones, indicamos como correcta la a).
Reactivo 18
Encuentre la solución al sistema de ecuaciones lineales representado por las rectas:
\begin{array}{c}x+2y=1\\ 2x-y=4\end{array}
- P\left(-\frac{9}{5}, \frac{2}{5}\right)
- P\left(-\frac{9}{5}, -\frac{2}{5}\right)
- P\left(\frac{9}{5}, -\frac{2}{5}\right)
- P\left(\frac{9}{5}, \frac{2}{5}\right)
Solución:
Para encontrar los valores de x y y que satisfacen al sistema de ecuaciones, debemos aplicar cualquiera de los métodos conocidos: sustitución, reducción, igualación o algún procedimiento con matrices.
Esta vez, debido a la simplicidad del SEL conviene emplear el método por reducción. Nuestro objetivo es sumar o restar las ecuaciones, donde alguna de ellas esté multiplicada por un número que nos permita cancelar una de las dos variables.
Debido a que la y está cambiada de signo en ambas ecuaciones, nos queda multiplicar la ecuación II:2x-y=4 por 2 para que al sumarla con I:x+2y=1 la y se cancele.
I+2II:
\begin{array}{c}x+2y=1\\ 4x-2y=8\end{array}
Sumamos las ecuaciones.
5x=9\to x=\frac{9}{5}
Sustituimos este resultado en cualquiera de las dos ecuaciones para obtener el valor de y . Lo haremos en la segunda ecuación.
y=2x-4\to y=2\left(\frac{9}{5}\right)-4
\therefore y=-\frac{2}{5}
Finalmente, la solución al sistema de ecuaciones es:
P\left(\frac{9}{5}, -\frac{2}{5}\right)=P\left(1.8, -0.4\right)
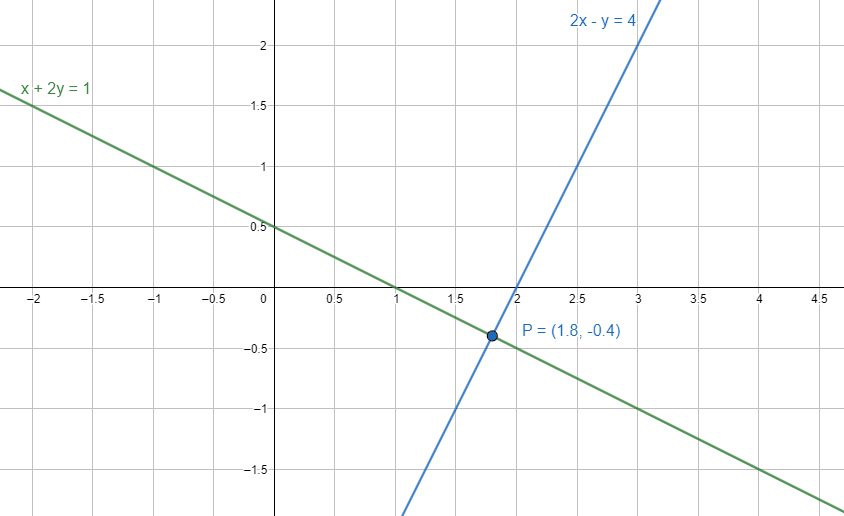
Concluimos seleccionando como respuesta correcta la opción c).
Reactivo 19
Factorice la siguiente expresión.
{y}^{2}+yx+yz+xz
- {z\left(y+x\right)}^{2}
- \left(y-x\right)\left(y+z\right)
- \left(y+x\right)\left(y-z\right)
- \left(y+x\right)\left(y+z\right)
Solución:
En este caso, el método de factorización que nos conviene utilizar es el de agrupación de términos. Agrupamos {y}^{2} con yx para extraer factor común la y y yz con xz para extraer factor común la z .
{y}^{2}+yx+yz+xz=\left({y}^{2}+yx\right)+\left(yz+xz\right)=y\left(y+x\right)+z\left(y+x\right)
Ahora, nos queda extraer factor común el binomio y+x .
y\left(y+x\right)+z\left(y+x\right)=\left(y+x\right)\left(y+z\right)
La forma factorizada de {y}^{2}+yx+yz+xz es \left(y+x\right)\left(y+z\right)
Comparando con las opciones, la correcta está en el inciso d).
Reactivo 20
Realice la siguiente división de polinomios:
\left({x}^{3}-2{x}^{2}+x+1\right)÷\left(x+1\right)
- {x}^{2}-3x+4-\frac{3}{x-1}
- {x}^{2}+3x+4-\frac{3}{x+1}
- {x}^{2}-3x+4-\frac{3}{x+1}
- {x}^{2}-3x+4+\frac{3}{x+1}
Solución:
Cuando el polinomio divisor es un binomio o superior, el único procedimiento para encontrar la división es aplicar el algoritmo de la división sintética. Comenzamos ordenando los polinomios:

El primer término del cociente será {x}^{2} para que, multiplicado por el divisor, nos permita eliminar el término {x}^{3} del dividendo.
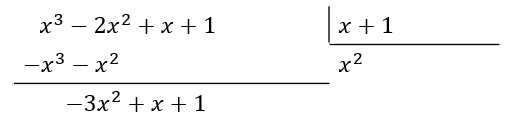
Ahora, para eliminar el término -3{x}^{2} el siguiente término del cociente será -3x .
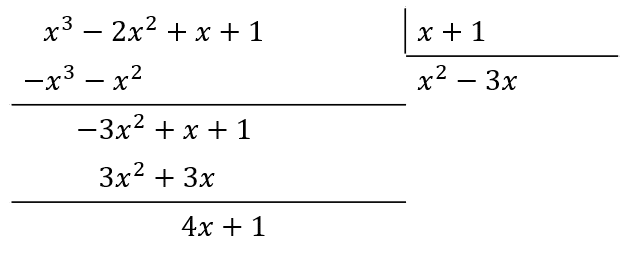
Finalmente, el término del sustraendo debe ser 4 para eliminar a 4x .
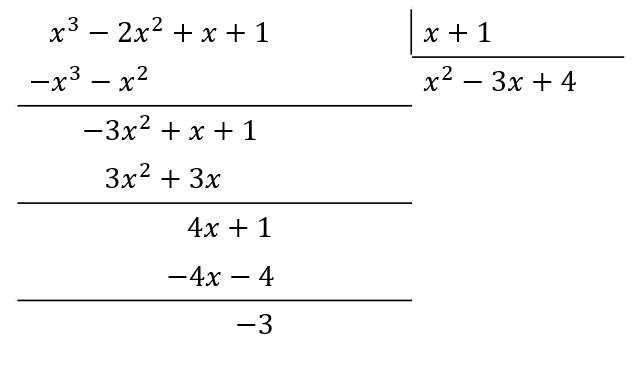
La división de los polinomios puede escribirse como:
\frac{{x}^{3}-2{x}^{2}+x+1}{x+1}={x}^{2}-3x+4-\frac{3}{x+1}
Comparando con los incisos, el correcto es el c).

