Vamos a resolver los siguientes 10 reactivos de la segunda versión del simulador de matemáticas para el examen de admisión al IPN en las áreas de IyCFM. En esta tercera parte resolveremos los reactivos del 21 al 30.

Reactivo 21
En el sistema de coordenadas polares, un punto viene descrito por:
- x, y
- x, r
- \theta , r
- y, \theta
Solución:
El sistema de coordenadas polares, permite la representación de puntos en el plano mediante dos coordenadas: un ángulo \theta y un radio vector r que se dibuja desde el centro o polo hasta el punto en cuestión.
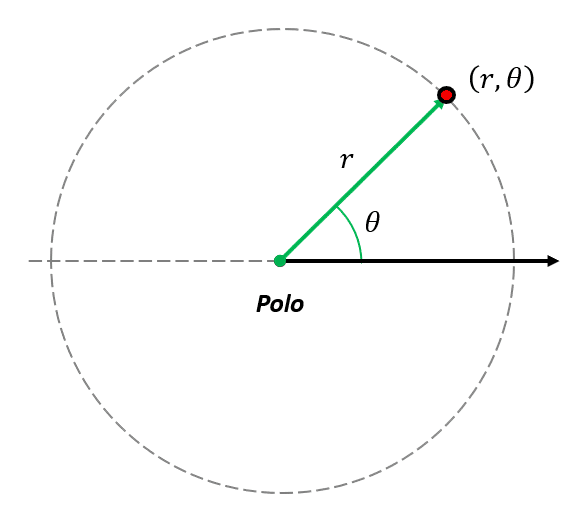
La respuesta correcta es el inciso c).
Reactivo 22
Escriba la ecuación de la familia de rectas perpendiculares a 2x-y+1=0 .
- y=-\frac{1}{2}x+b
- y=\frac{1}{2}x+b
- y=-\frac{1}{2}x
- y=-2x+b
Solución:
Iniciemos escribiendo la ecuación punto pendiente de la recta.
y-{y}_{o}=m\left(x-{x}_{o}\right)
Si desarrollamos la expresión nos queda:
y=mx+{y}_{o}-{x}_{o}
A la diferencia {y}_{o}-{x}_{o} la llamaremos b y será el parámetro de la familia de curvas.
y=mx+b
Esta es la forma explícita de la recta. Solo queda calcular la pendiente que, teniendo en cuenta la condición de perpendicularidad, la pendiente de la familia de rectas es:
{m}_{2}=-\frac{1}{{m}_{1}}
Donde {m}_{1} es la pendiente de la recta dada.
2x-y+1=0\to y=2x+1\to {m}_{1}=2
Sustituimos.
{m}_{2}=-\frac{1}{2}
La ecuación de la familia de rectas perpendiculares a 2x-y+1=0 es:
y=-\frac{1}{2}x+b
La respuesta correcta es el inciso a).
Reactivo 23
Calcule la pendiente de la recta que tiene como ecuación:
3x-4y+2=0
- m=\frac{3}{4}
- m=-\frac{3}{4}
- m=3
- m=4
Solución:
En este caso, debemos transformar a la recta a su forma explícita despejando a la variable y .
3x-4y+2=0\to -4y=-3x-2
y=\frac{3}{4}x+\frac{1}{2}
La pendiente de la recta es el coeficiente que acompaña a la x .
m=\frac{3}{4}
La respuesta correcta es el inciso a).
Reactivo 24
Si una recta corta con los ejes coordenados en los puntos \left(4, 0\right) y \left(0, 6\right) , ¿cuánto vale la tangente del ángulo de inclinación de la recta?
- 4
- \frac{2}{3}
- -\frac{3}{2}
- \frac{3}{2}
Solución:
Comencemos recordando que la tangente del ángulo de inclinación de una recta es igual a su pendiente.
\mathrm{tan}\alpha =m
Ahora, con los puntos de intersección con los ejes ¿cómo se calcula la pendiente? Hagamos un dibujo de la situación.
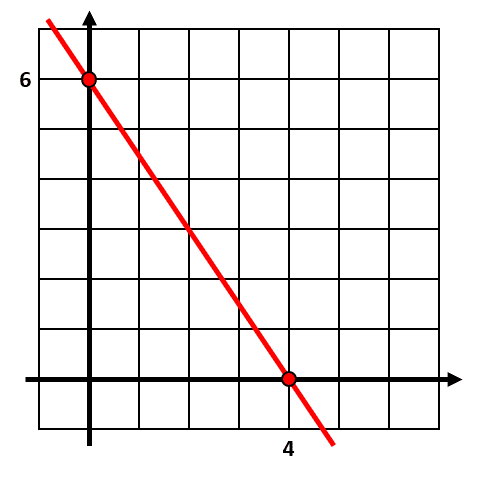
La pendiente se calcula como el cociente del corte en y con el corte en x . Lleva signo negativo porque la recta está inclinada a la izquierda.
\mathrm{tan}\alpha =-\frac{6}{4}=-\frac{3}{2}
La tangente del ángulo de inclinación de la recta es -\frac{3}{2} .
La respuesta correcta es el inciso c).
Reactivo 25
¿Cuál es la ecuación general de la circunferencia con centro en \left(1, 0\right) y radio igual a 4?
- {x}^{2}+{y}^{2}-2x+15=0
- {x}^{2}+{y}^{2}-2x-15=0
- {x}^{2}-{y}^{2}-2x-15=0
- {x}^{2}+{y}^{2}+2x-15=0
Solución:
Comenzamos sustituyendo el centro y el radio en la ecuación de la circunferencia.
{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}
{\left(x-1\right)}^{2}+{y}^{2}=16
Ahora, desarrollamos el binomio al cuadrado.
{x}^{2}-2x+1+{y}^{2}=16
Reacomodando.
{x}^{2}+{y}^{2}-2x-15=0
De forma gráfica.
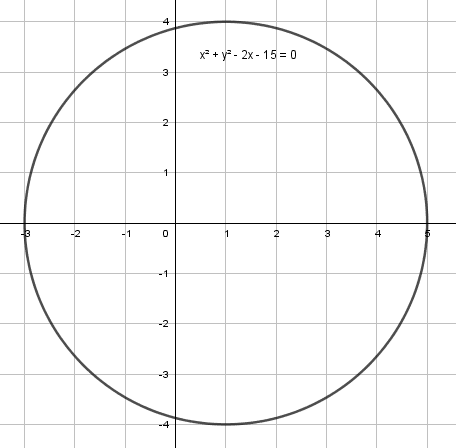
La respuesta correcta es el inciso b).
Reactivo 26
Encuentre la derivada de la función:
f\left(x\right)=\sqrt[4]{\sqrt[3]{x}}
- \frac{1}{\sqrt[12]{{x}^{11}}}
- \frac{1}{12\sqrt[12]{{x}^{11}}}
- \frac{1}{12\sqrt[11]{{x}^{12}}}
- \frac{\sqrt[12]{{x}^{11}}}{12}
Solución:
Aunque la función del enunciado parezca compleja, podemos simplificar su aspecto expresando las raíces como potencias.
f\left(x\right)={\left({\left(x\right)}^{\frac{1}{3}}\right)}^{\frac{1}{4}}
Ahora, aplicamos potencia de una potencia.
f\left(x\right)={\left(x\right)}^{\frac{1}{12}}
Empleamos la fórmula de la derivada de una potencia.
{f}^{\text{'}}\left(x\right)=\frac{1}{12}{x}^{\frac{1}{12}-1}=\frac{1}{12}{x}^{-\frac{11}{12}}=\frac{1}{12\sqrt[12]{{x}^{11}}}
Concluimos indicando como respuesta correcta al inciso b).
Reactivo 27
Calcule el intervalo solución de la siguiente desigualdad:
\frac{2x-3}{2}\le \frac{x+1}{3}
- x\in \left(-\infty ,\frac{11}{4}\right]
- x\in \left(-\infty ,\frac{11}{4}\right)
- x\in \left(\frac{11}{4}, \infty \right)
- x\in \left(-\infty ,-\frac{11}{4}\right]
Solución:
Recordemos que las desigualdades se resuelven de forma similar a las igualdades, la única diferencia es que cuando multiplicamos o dividimos por un número negativo la desigualdad cambia de sentido.
Comenzamos multiplicando por los denominadores de ambos lados.
\frac{2x-3}{2}\le \frac{x+1}{3}\to 2x-3\le \frac{2\left(x+1\right)}{3}
2x-3\le \frac{2\left(x+1\right)}{3}\to 3\left(2x-3\right)\le 2\left(x+1\right)
Resolvemos las distributivas.
6x-9\le 2x+2
Simplificamos.
6x-2x\le 2+9\to 4x\le 11
x\le \frac{11}{4}
La inecuación se cumple para todo x menor o igual que \frac{11}{4} . En notación de conjunto:
x\in \left(-\infty ,\frac{11}{4}\right]
La respuesta correcta es el inciso a).
Reactivo 28
Encuentre el valor del siguiente límite.
\underset{x\to -1}{\mathrm{lim}}\frac{x+1}{{x}^{2}-2x-3}
- -1
- \nexists
- -\frac{1}{4}
- \frac{1}{4}
Solución:
Lo primero que hacemos antes de resolver cualquier límite, es evaluarlo para verificar si hay indeterminación.
\underset{x\to -1}{\mathrm{lim}}\frac{x+1}{{x}^{2}-2x-3}=\frac{-1+1}{{\left(-1\right)}^{2}-2\left(-1\right)-3}=\frac{0}{0}
Tenemos una indeterminación 0/0. Comenzamos factorizando el denominador.
{x}^{2}-2x-3=\left(x+1\right)\left(x-3\right)
Sustituimos en el límite y simplificamos.
\underset{x\to -1}{\mathrm{lim}}\frac{x+1}{{x}^{2}-2x-3}=\underset{x\to -1}{\mathrm{lim}}\frac{x+1}{\left(x+1\right)\left(x-3\right)}=\underset{x\to -1}{\mathrm{lim}}\frac{1}{x-3}
Evaluamos el límite para comprobar.
\underset{x\to -1}{\mathrm{lim}}\frac{1}{x-3}=\frac{1}{-1-3}=-\frac{1}{4}
El límite de \frac{x+1}{{x}^{2}-2x-3} cuando x tiende a -1 es -\frac{1}{4} .
La respuesta correcta es el inciso c).
Reactivo 29
El límite \underset{x\to 1}{\mathrm{lim}}\left[\mathrm{ln}\left(\frac{1}{x+1}\right)\right] es igual a…
- \mathrm{ln}\left(2\right)
- \mathrm{ln}\left(1\right)
- \mathrm{ln}\left(1\right)+\mathrm{ln}\left(2\right)
- \mathrm{ln}\left(1\right)-\mathrm{ln}\left(2\right)
Solución:
Para resolver este límite, debemos aplicar la siguiente propiedad:
\underset{x\to a}{\mathrm{lim}}\left[\mathrm{log}f\left(x\right)\right]=\mathrm{log}\left[\underset{x\to a}{\mathrm{lim}}f\left(x\right)\right]
Llevando esto a nuestra función nos queda:
\underset{x\to 1}{\mathrm{lim}}\left[\mathrm{ln}\left(\frac{1}{x+1}\right)\right]=\mathrm{ln}\left[\underset{x\to 1}{\mathrm{lim}}\frac{1}{x+1}\right]
Evaluamos el límite.
\mathrm{ln}\left[\underset{x\to 1}{\mathrm{lim}}\frac{1}{x+1}\right]=\mathrm{ln}\left[\frac{1}{1+1}\right]=\mathrm{ln}\left(\frac{1}{2}\right)
Aplicamos la propiedad del logaritmo del cociente para asemejar el resultado a los incisos.
\mathrm{ln}\left(\frac{1}{2}\right)=\mathrm{ln}\left(1\right)-\mathrm{ln}\left(2\right)
Finalmente:
\underset{x\to 1}{\mathrm{lim}}\left[\mathrm{ln}\left(\frac{1}{x+1}\right)\right]=\mathrm{ln}\left(1\right)-\mathrm{ln}\left(2\right)
La respuesta correcta es el inciso d).
Reactivo 30
Ordene, de menor a mayor, el resultado de evaluar las derivadas de las siguientes funciones en el punto x=1 .
- f\left(x\right)=\frac{1}{x+1}
- g\left(x\right)=-\frac{x}{2x+1}
- h\left(x\right)=2{x}^{2}-3
- q\left(x\right)=\sqrt{4-2x}
- 4, 1, 2, 3
- 1, 4, 2, 3
- 4, 2, 1, 3
- 3, 2, 1, 4
Solución:
Debido a que el ordenamiento se hace a partir de sus derivadas, debemos comenzar por calcular sus derivadas.
Derivada de f\left(x\right) .
{f}^{\text{'}}\left(x\right)={\left(\frac{1}{x+1}\right)}^{\text{'}}=-\frac{1}{{\left(x+1\right)}^{2}}
Derivada de g\left(x\right) .
{g}^{\text{'}}\left(x\right)={\left(-\frac{x}{2x+1}\right)}^{\text{'}}=-\frac{2x+1-2x}{{\left(2x+1\right)}^{2}}=-\frac{1}{{\left(2x+1\right)}^{2}}
Derivada de h\left(x\right) .
{h}^{\text{'}}\left(x\right)={\left(2{x}^{2}-3\right)}^{\text{'}}=4x
Derivada de q\left(x\right) .
{q}^{\text{'}}\left(x\right)={\left(\sqrt{4-2x}\right)}^{\text{'}}=-\frac{1}{\sqrt{4-2x}}
Evaluamos las derivadas en el punto dado.
{f}^{\text{'}}\left(x=1\right)=-\frac{1}{{\left(1+1\right)}^{2}}=-\frac{1}{4}=-0.25
{g}^{\text{'}}\left(x=1\right)=-\frac{1}{{\left(2\left(1\right)+1\right)}^{2}}=-\frac{1}{9}\approx -0.111
{h}^{\text{'}}\left(x=1\right)=4\left(1\right)=4
{q}^{\text{'}}\left(x=1\right)=-\frac{1}{\sqrt{4-2\left(1\right)}}=-\frac{1}{\sqrt{2}}\approx -0.707
Teniendo estos valores, ordenamos ahora de menor a mayor.
{q}^{\text{'}}\to {f}^{\text{'}}\to {g}^{\text{'}}\to {h}^{\text{'}}
Sustituyendo el número de las funciones.
4, 1, 2, 3
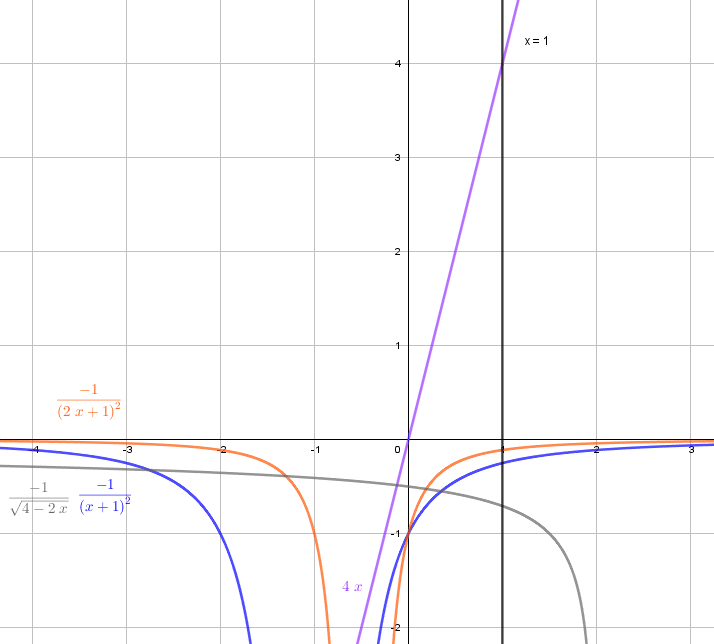
La respuesta correcta es el inciso a).


