Examen simulacro IPN Cs. Sociales Administrativas | Matemáticas P. 2

Vamos con los ejercicios del 31 al 40, correspondientes a la segunda parte del simulador de matemáticas para el examen de ingreso al IPN en el área de Ciencias Sociales y Administrativas.

Estudia los fundamentos de cada tema, no importa la cantidad de reactivos que resuelvas sino, tu capacidad de análisis ante cada problema.

Ejercicios de Matemáticas

Vamos con la solucion de los siguientes 10 reactivos del simulador de matemáticas, para la prueba de ingreso del Instituto Politécnico Nacional en el área de las Ciencias Sociales y Administrativas.

Reactivo 31

Estudiando la continuidad sobre una función a trozos, se encontró que el límite en x\to {a}^{+} es distinto al límite cuando x\to {a}^{-} . ¿Cuál de las siguientes conclusiones es correcta?

1. Es continua en ese punto según la dirección de proximidad
2. La función no es continua en ese punto
3. Es necesario revisar ahora la derivada de la función en ese punto
4. Los límites laterales nunca son diferentes

Solución:

Para responder correctamente a esta pregunta, debemos recordar las condiciones de continuidad.

1. El valor x=a debe pertenecer al dominio de la función
2. El límite en x\to a de f debe existir
3. La función evaluada en el punto debe existir
4. El límite y la función evaluada en el punto deben ser iguales

Para la función a trozos del enunciado, tenemos que suponer las condiciones 1 y 3, para concentrarnos en la condición 2. Cuando evaluamos los límites laterales de una función, buscamos que sean iguales para concluir que el límite existe, en caso contrario no existe.

Debido a que los límites laterales {a}^{-} y {a}^{+} son distintos y el límite no existe, por ende, la condición 2 se rompe y la función no es continua para x=a . En base a nuestro análisis, la respuesta correcta es el inciso b).

Reactivo 32

Calcule la derivada de la siguiente función.

f\left(x\right)={e}^{4x-1}

1. {f}^{\text{'}}\left(x\right)=4\cdot {e}^{4x-1}
2. {f}^{\text{'}}\left(x\right)={e}^{4x-1}
3. {f}^{\text{'}}\left(x\right)=\frac{1}{4}\cdot {e}^{4x-1}
4. {f}^{\text{'}}\left(x\right)=-4{e}^{4x-1}

Solución:

Para esta función en particular, debemos emplear la fórmula de la derivada de e .

\frac{d{e}^{f\left(x\right)}}{dx}={f}^{\text{'}}\left(x\right){e}^{f\left(x\right)}

Aplicando a la función:

\frac{d\left({e}^{4x-1}\right)}{dx}={\left(4x-1\right)}^{\text{'}}{e}^{4x-1}=4{e}^{4x-1}

Finalmente:

{f}^{\text{'}}\left(x\right)=4{e}^{4x-1}

La respuesta correcta es el inciso a).

Reactivo 33

Cuando la variable x tiende a infinito, el valor de la función f\left(x\right) tiende a un valor finito f\left(x\to \infty \right)=a . ¿Cuál de las siguientes aseveraciones es correcta?

1. Tiene una asíntota en y=a
2. Tiene una asíntota en y=-a
3. Tiene una asíntota en x=a
4. Tiene una asíntota en x=-a

Solución:

Las asíntotas de una función, vienen representadas como rectas en el plano donde la distancia entre la gráfica de la función y la recta es cada vez más pequeña, pero nunca llegan a ser iguales.

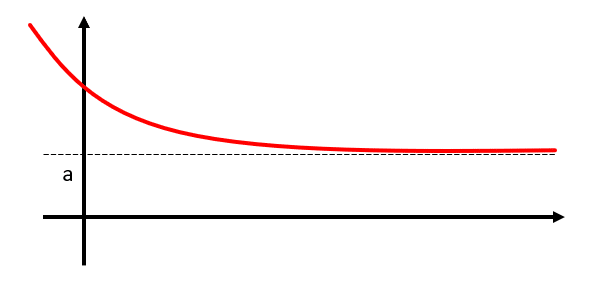
Ya que los valores que toma la variable se presentan en el eje y , la recta que representa a la asíntota es una recta horizontal y=a . Concluimos que la respuesta correcta es el inciso a).

Reactivo 34

Encuentre la descomposición en fracciones parciales de la siguiente expresión.

\frac{{x}^{2}+1}{x\left(x+1\right)\left(x+2\right)\left(x-1\right)}

1. -\frac{1}{2x}+\frac{1}{x+1}-\frac{5}{6\left(x+2\right)}+\frac{1}{3\left(x-1\right)}
2. \frac{1}{2x}+\frac{1}{x+1}-\frac{5}{6\left(x+2\right)}+\frac{1}{3\left(x-1\right)}
3. -\frac{1}{2x}+\frac{1}{x+1}-\frac{5}{6\left(x+2\right)}-\frac{1}{3\left(x-1\right)}
4. -\frac{1}{2x}-\frac{1}{x+1}-\frac{5}{6\left(x+2\right)}+\frac{1}{3\left(x-1\right)}

Solución:

El método de fracciones parciales, nos permite separas a una fracción compleja donde el grado del numerador es menor al grado del denominador, en varias fracciones simples. El procedimiento tiene especial utilidad en cálculo integral.

Se iguala la fracción original a la suma de varias fracciones cuyo denominador es cada uno de los factores del denominador original.

\frac{{x}^{2}+1}{x\left(x+1\right)\left(x+2\right)\left(x-1\right)}=\frac{A}{x}+\frac{B}{x+1}+\frac{C}{x+2}+\frac{D}{x-1}

Debemos resolver la igualdad para luego aplicar igualación de términos.

{x}^{2}+1=A\left(x+1\right)\left(x+2\right)\left(x-1\right)+Bx\left(x+2\right)\left(x-1\right)+Cx\left(x+1\right)\left(x-1\right)+Dx\left(x+1\right)\left(x+2\right)

Desarrollamos los productos de cada término.

=A\left({x}^{3}+2{x}^{2}-x-2\right)+B\left({x}^{3}+{x}^{2}-2x\right)+C\left({x}^{3}-x\right)+D\left({x}^{3}+3{x}^{2}+2x\right)

Agrupamos términos semejantes.

{x}^{2}+1=\left(A+B+C+D\right){x}^{3}+\left(2A+B+3D\right){x}^{2}+\left(-A-2B-C+2D\right)x-2A

Igualamos los coeficientes de los polinomios.

\begin{array}{c}A+B+C+D=0\\ 2A+B+3D=1\\ \begin{array}{c}-A-2B-C+2D=0\\ -2A=1\end{array}\end{array}

Ahora nos queda resolver el sistema de ecuaciones. Despejamos el valor de A y sustituimos en el resto de ecuaciones.

-2A=1\to A=-\frac{1}{2}

\left\{\begin{array}{c}B+C+D=\frac{1}{2}\\ B+3D=2\\ -2B-C+2D=-\frac{1}{2}\end{array}\right.

Para resolver este sistema 3×3 puedes emplear la regla de Cramer o el método por eliminación. Saltaremos este paso para evitar desviar la intención principal del ejercicio. El valor de los coeficientes es:

\begin{array}{c}A=-\frac{1}{2}\\ B=1\\ \begin{array}{c}C=-\frac{5}{6}\\ D=\frac{1}{3}\end{array}\end{array}

Sustituyendo en la descomposición inicial nos queda:

=-\frac{1}{2x}+\frac{1}{x+1}-\frac{5}{6\left(x+2\right)}+\frac{1}{3\left(x-1\right)}

La respuesta correcta es el inciso a).

Reactivo 35

Calcule el resultado de la siguiente integral.

\int \left({x}^{2}-3x-\frac{1}{x}\right)dx

1. -\frac{{x}^{3}}{3}-\frac{3{x}^{2}}{2}-\mathrm{ln}\left|x\right|+C
2. \frac{{x}^{3}}{3}-\frac{3{x}^{2}}{2}-\mathrm{ln}\left|x\right|+C
3. -\frac{{x}^{3}}{3}+\frac{3{x}^{2}}{2}-\mathrm{ln}\left|x\right|+C
4. \frac{{x}^{3}}{3}-\frac{3{x}^{2}}{2}+\mathrm{ln}\left|x\right|+C

Solución:

Iniciamos aplicando la propiedad de la integral de la suma:

\int \left({x}^{2}-3x-\frac{1}{x}\right)dx=\int {x}^{2}dx-3\int xdx-\int \frac{1}{x}dx

Las tres integrales resultantes se resuelven aplicando fórmulas inmediatas.

\int {x}^{2}dx-3\int xdx-\int \frac{1}{x}dx=\frac{{x}^{3}}{3}-\frac{3}{2}{x}^{2}-\mathrm{ln}x+C

Finalmente:

\int \left({x}^{2}-3x-\frac{1}{x}\right)dx=\frac{{x}^{3}}{3}-\frac{3}{2}{x}^{2}-\mathrm{ln}x+C

La respuesta correcta es el inciso b).

Reactivo 36

¿Cómo queda el integrando de la integral indefinida que se muestra a continuación, luego de aplicar fracciones parciales?

\int \frac{2x-1}{\left(x-3\right)\left(x-2\right)\left(x-1\right)}dx

1. \frac{5}{2\left(x-3\right)}-\frac{3}{x-2}+\frac{1}{2\left(x-1\right)}
2. \frac{1}{2\left(x-3\right)}-\frac{3}{x-2}+\frac{1}{2\left(x-1\right)}
3. \frac{5}{2\left(x-3\right)}+\frac{3}{x-2}+\frac{1}{2\left(x-1\right)}
4. -\frac{1}{2\left(x-3\right)}-\frac{3}{x-2}-\frac{1}{2\left(x-1\right)}

Solución:

El enunciado nos dice directamente que apliquemos fracciones parciales. Comenzamos igualando la fracción compleja a su descomposición.

\frac{2x-1}{\left(x-3\right)\left(x-2\right)\left(x-1\right)}=\frac{A}{x-3}+\frac{B}{x-2}+\frac{C}{x-1}

Pasamos a multiplicar el denominador del miembro izquierdo.

2x-1=A\left(x-2\right)\left(x-1\right)+B\left(x-3\right)\left(x-1\right)+C\left(x-3\right)\left(x-2\right)

Desarrollamos los productos indicados.

2x-1=A\left({x}^{2}-3x+2\right)+B\left({x}^{2}-4x+3\right)+C\left({x}^{2}-5x+6\right)

Agrupamos términos semejantes.

2x-1=\left(A+B+C\right){x}^{2}+\left(-3A-4B-5C\right)x+2A+3B+6C

Igualamos los coeficientes de ambos polinomios.

\begin{array}{c}A+B+C=0\\ -3A-4B-5C=2\\ 2A+3B+6C=-1\end{array}

Similar al ejercicio anterior, evitaremos expandir la solución del SEL porque evade las intensiones del ejercicio. Aplicando cualquier método de solución obtenemos que:

A=\frac{5}{2}, C=\frac{1}{2}, B=-3

Sustituyendo en la expresión:

=\frac{5}{2\left(x-3\right)}-\frac{3}{x-2}+\frac{1}{2\left(x-1\right)}

Comparando con los incisos, concluimos que la respuesta correcta es el a).

Reactivo 37

Hallar la integral indefinida.

\int \left(2{x}^{2}-3x+\frac{4}{x}\right)dx

1. \frac{2{x}^{3}}{3}-\frac{3{x}^{2}}{2}+4\mathrm{ln}\left|x\right|+C
2. \frac{2{x}^{3}}{3}-\frac{3{x}^{2}}{2}-4\mathrm{ln}\left|x\right|+C
3. -\frac{2{x}^{3}}{3}-\frac{3{x}^{2}}{2}+4\mathrm{ln}\left|x\right|+C
4. \frac{{x}^{3}}{3}-\frac{{x}^{2}}{2}+4\mathrm{ln}\left|x\right|+C

Solución:

Iniciamos separando la integral en tres integrales sencillas.

\int \left(2{x}^{2}-3x+\frac{4}{x}\right)dx=2\int {x}^{2}dx-3\int x+4\int \frac{dx}{x}

Ahora, empleamos las fórmulas de la integral de una potencia y del inverso de x .

2\int {x}^{2}dx-3\int x+4\int \frac{dx}{x}=\frac{2}{3}{x}^{3}-\frac{3}{2}{x}^{2}+\mathrm{ln}x+C

Finalmente:

\int \left(2{x}^{2}-3x+\frac{4}{x}\right)dx=\frac{2}{3}{x}^{3}-\frac{3}{2}{x}^{2}+\mathrm{ln}x+C

La respuesta correcta es el inciso a).

Reactivo 38

Calcule el valor de la integral definida.

i={\int }_{0}^{4}{x}^{2}dx

1. 64/3
2. 64
3. 1/3
4. -64/3

Solución:

Para resolver integrales definidas, aplicamos el primer teorema fundamental del cálculo.

{\int }_{a}^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right)

Donde F es la primitiva de f . Iniciamos integrando indefinidamente.

{\int }_{0}^{4}{x}^{2}dx=\begin{array}{c} \\ \frac{{x}^{3}}{3}\\  \end{array}⟧\begin{array}{c}4\\  \\ 0\end{array}

Evaluamos:

\begin{array}{c} \\ \frac{{x}^{3}}{3}\\  \end{array}⟧\begin{array}{c}4\\  \\ 0\end{array}=\frac{{\left(4\right)}^{3}}{3}-0=\frac{64}{3}

Comparando con los incisos, indicamos al a) como respuesta correcta.

Reactivo 39

¿Cuál es el valor de la siguiente integral definida?

i={\int }_{1}^{3}\frac{dx}{{x}^{2}}

1. \frac{2}{3}
2. \frac{1}{3}
3. 2
4. -\frac{2}{3}

Solución:

Iniciamos integrando a la función indefinidamente, dejando indicados los extremos.

{\int }_{1}^{3}\frac{dx}{{x}^{2}}={\int }_{1}^{3}{x}^{-2}dx=\begin{array}{c} \\ \frac{{x}^{-1}}{-1}\\  \end{array}⟧\begin{array}{c}3\\  \\ 1\end{array}=\begin{array}{c} \\ -\frac{1}{x}\\  \end{array}⟧\begin{array}{c}3\\  \\ 1\end{array}

Evaluamos:

\begin{array}{c} \\ -\frac{1}{x}\\  \end{array}⟧\begin{array}{c}3\\  \\ 1\end{array}=-\frac{1}{3}+1=\frac{2}{3}

El valor de la integral definida es \frac{2}{3} .

Indicamos al inciso a) como respuesta correcta.

Reactivo 40

Calcule el valor de la integral.

{\int }_{-1}^{1}\left(2x-{x}^{3}\right)dx

1. 1
2. \infty
3. 0
4. -1

Solución:

Separamos la integral aplicando la propiedad de la integral de la suma.

{\int }_{-1}^{1}\left(2x-{x}^{3}\right)dx=2{\int }_{-1}^{1}xdx-{\int }_{-1}^{1}{x}^{3}dx

Integramos indefinidamente e indicamos los límites.

2{\int }_{-1}^{1}xdx-{\int }_{-1}^{1}{x}^{3}dx=\left(\begin{array}{c} \\ {x}^{2}-\frac{{x}^{4}}{4}\\  \end{array}\right]\begin{array}{c}1\\  \\ -1\end{array}=\left({1}^{2}-\frac{{1}^{4}}{4}\right)-\left[{\left(-1\right)}^{2}-\frac{{\left(-1\right)}^{4}}{4}\right]=\frac{3}{4}-\frac{3}{4}=0

Finalmente:

{\int }_{-1}^{1}\left(2x-{x}^{3}\right)dx=0

Esto significa que la función es simétrica respecto al origen.