Continúa resolviendo la tercera y última parte del simulador de matemáticas para el área de Ciencias Sociales y Administrativas del Instituto Politécnico Nacional.

Matemáticas es solo una de las asignaturas que deberás presentar en el examen. Continúa aprendiendo con el resto de guías que hemos diseñado para ti.
Ejercicios de Matemáticas
Finalmente, vamos con los últimos 10 reactivos de matemáticas del simulacro para el área de Ciencias Sociales y Administrativas del IPN.
Reactivo 41
Dados dos conjuntos con cualesquiera elementos mutuamente excluyentes, ¿cuál de las siguientes opciones representa su intersección?
- \left\{\varnothing \right\}
- U-A
- U-B
- U
Solución:
Recordando la teoría sobre teoría de conjuntos, dos conjuntos mutuamente excluyentes poseen elementos distintos uno de otro, es decir, no poseen elementos en común. Si intentamos interceptarlos, operación que mantiene a los elementos comunes, el resultado será vacío.
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 42
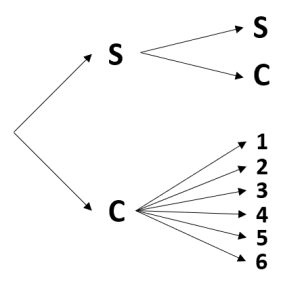
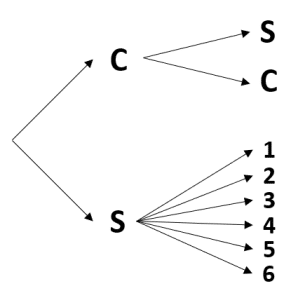
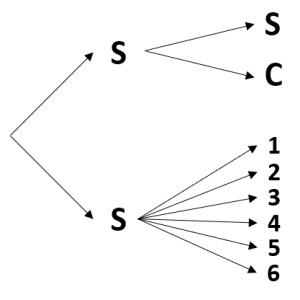
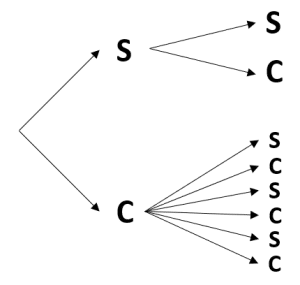
En un experimento aleatorio, se lanza un dado, y si cae “sol” se lanza una segunda vez y termina el experimento. Por otra parte, si cae “cruz” se tira un dado y luego termina el experimento. ¿Cuál de los siguientes diagramas de árbol representa al experimento anteriormente descrito?
Solución:
Para encontrar el diagrama de árbol del experimento descrito en el enunciado, debemos ir paso a paso con cada uno de los eventos. Primero, se lanza una moneda cuyos resultados posibles son Sol y Cruz.
Ahora, si cae Sol las opciones que tenemos es volver a lanzar la moneda cuyas posibilidades vuelven a ser Sol y Cruz.
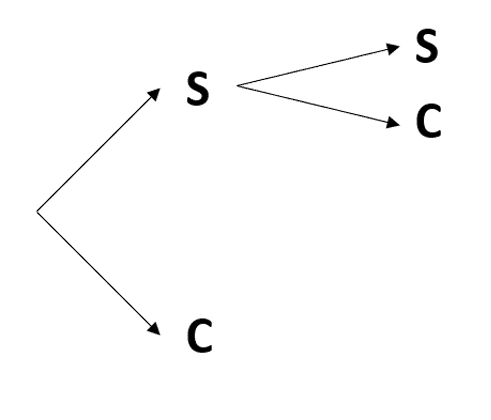
Por otro lado, si cae Cruz se debe tirar un dado cuyas posibilidades son los números del 1 al 6.
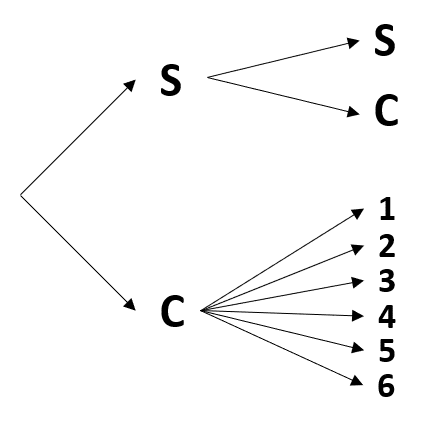
Comparando el resultado con las opciones, concluimos que la respuesta correcta es la a).
Reactivo 43
Expresar por extensión el conjunto siguiente:
A=\left\{x|x \mathrm{e}\mathrm{s}\mathrm{ }\mathrm{u}\mathrm{n}\mathrm{ }\mathrm{d}\mathrm{í}\mathrm{g}\mathrm{i}\mathrm{t}\mathrm{o}\mathrm{ }\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{ }\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{l}\mathrm{a}\mathrm{ }\mathrm{c}\mathrm{i}\mathrm{f}\mathrm{r}\mathrm{a}\mathrm{ }1524679\right\}
- \left\{2, 4, 6\right\}
- \left\{4, 6\right\}
- \left\{2, 4\right\}
- \left\{\varnothing \right\}
Solución:
La descripción general de conjunto nos dice que debe contener las cifras pares de 1524679 , es decir:
A=\left\{2, 4, 6\right\}
Concluimos que la respuesta correcta es el inciso a).
Reactivo 44
Se ha realizado una encuesta a los trabajadores de una empresa, sobre la cantidad de personas que conforman su núcleo familiar, a continuación, se presentan los resultados.
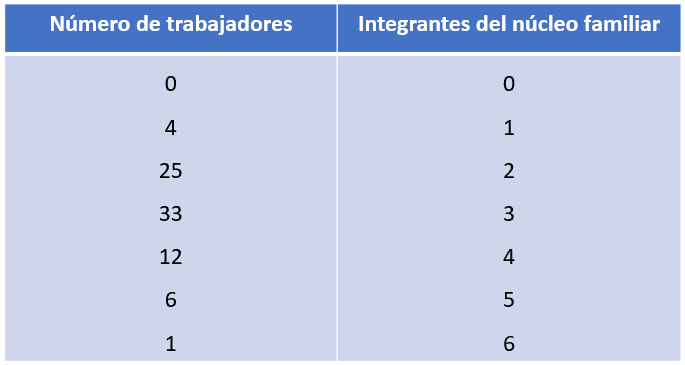
Indique la moda del conjunto de datos.
- 4
- 2
- 3
- 1
Solución:
Recordemos que la moda, es el parámetro estadístico que indica cuál es el elemento que mayor cantidad de veces se repite en la muestra. En este caso, no tenemos al conjunto de datos individualmente sino, expresados en una tabla.
En la columna izquierda vemos al número de familias y en la derecha a los integrantes del núcleo familiar. Tengamos en cuenta, que la cantidad de familias es nuestra frecuencia absoluta, por tanto, el dato con la mayor {f}_{i} corresponderá a la moda.
Examinando la tabla, concluimos que la respuesta correcta es: un núcleo familiar de 3 integrantes.
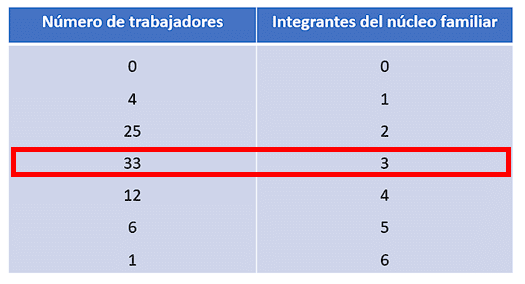
Seleccionamos al inciso c).
Reactivo 45
La fórmula que permite calcular el número de arreglos de m cantidad de objetos, en los que importa el orden es…
- m!
- m!+1
- m\left(m-1\right)\left(m-2\right)
- \left(m-1\right)!
Solución:
Inicialmente, el enunciado indica la importancia del orden, por tanto, se trata de una permutación. Ahora, tenemos 3 ecuaciones diferentes para calcular permutaciones/variaciones:
P=m!, P={m}^{n}, P=m\left(m-1\right)\left(m-2\right)\dots
Regresando al enunciado, éste indica que los arreglos son de una m cantidad de objetos y como no se menciona un n , podemos estar seguros que se trata de una permutación en la que intervienen todos los elementos:
P=m!
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 46
Sean los conjuntos: A=\left\{1, 2, 4, 5\right\} y B=\left\{3, 2, 5, 7\right\} , calcule la diferencia B-A .
- \left\{3, 2, 5, 7\right\}
- \left\{\varnothing \right\}
- \left\{3, 7\right\}
- \left\{1, 3, 4, 7\right\}
Solución:
La diferencia de conjuntos es una operación que da como resultado a otro conjunto con los elementos del conjunto sustraendo que no se encuentran en el conjunto minuendo. Dicho en el contexto del problema, los elementos de B que no están en A.
B-A=\left\{3, 2, 5, 7\right\}-\left\{1, 2, 4, 5\right\}=\left\{3, 7\right\}
La respuesta correcta es el inciso c).
Reactivo 47
Encuentre el conjunto que origina a la siguiente partición.
S=\left\{\left\{\mathrm{1,4}\right\}, \left\{5, 7\right\}, \left\{9\right\}\right\}
- \left\{1, 4, 5, 7\right\}
- \left\{1, 4\right\}
- \left\{4, 5\right\}
- \left\{1, 4, 5, 7, 9\right\}
Solución:
La partición de un conjunto, consta en separar al mismo en subconjuntos no vacíos que contienen elementos del conjunto original y que son mutuamente excluyentes, es decir, no se repiten elementos entre particiones.
Para encontrar el conjunto original, basta con unir las particiones.
U=\left\{\mathrm{1,4}\right\}\cup \left\{\mathrm{5,7}\right\}\cup \left\{9\right\}=\left\{1, 4, 5, 7, 9\right\}
Finalmente, indicamos al inciso d) como la respuesta correcta.
Reactivo 48
¿Cuántos códigos de 3 letras se pueden formar con las vocales, teniendo en cuenta que pueden repetirse?
- 125
- 243
- 15
- 150
Solución:
Comencemos recordando que el conjunto de elementos que deseamos ordenas en grupos de 3, está conformado por 5 letras:
A, E, I, O, U
Ahora, el enunciado nos dice que se desean formar códigos, por tanto, importa el orden entre las letras, porque no será igual AEI que IEA y como no intervienen todos los elementos, concluimos que se trata de una variación con elementos repetidos:
{V}_{m}^{n}={m}^{n}
En este caso: m=5 y n=3 .
{V}_{5}^{3}={5}^{3}=125
Se pueden crear 125 códigos distintos.
La respuesta correcta es el inciso a).
Reactivo 49
Si el consejo estudiantil de una universidad mexicana está formado por 8 estudiantes de distintos años, ¿cuántas juntas directivas pueden conformarse si hay puesto para 1 presidente, un secretario y un vocero institucional?
- 326
- 336
- 346
- 356
Solución:
Para resolver este problema de conteo, comenzamos estableciendo que el total es 8 y que se deben ordenar en grupos de 3. Por otra parte, ya que se distingue una jerarquía entre los 3 puestos, no será igual que 3 estudiantes A, B y C queden seleccionados ABC que BCA. Importa el orden.
Finalmente, no participan todos los elementos y evidentemente no se permiten repeticiones, un mismo estudiante no puede ser presidente y secretario. Se trata de una variación ordinaria.
{V}_{m}^{n}=\frac{m!}{\left(m-n\right)!}
Sustituyendo:
{V}_{8}^{3}=\frac{8!}{\left(8-5\right)!}=8\times 7\times 6=336
La respuesta correcta es el inciso b).
Reactivo 50
Un grupo de amigos conformado por 6 estudiantes va a una cafetería con mesas redondas y uno de ellos se pregunta: ¿de cuántas formas distintas podemos sentarnos en la mesa de la cafetería?
- 105
- 110
- 115
- 120
Solución:
La situación que describe el enunciado, corresponde con una permutación circular. Es un tipo especial de permutaciones que se utiliza en los casos donde queremos ordenar a un grupo de elementos en forma circular.
La ecuación que las describe es:
P{C}_{m}=\left(m-1\right)!
Se le resta un elemento, porque se toma como referencia a este para cambiar de lugar al resto. Sustituyendo:
P{C}_{6}=\left(6-1\right)!=120
Concluimos que la respuesta correcta es el inciso d).