¡Aspirante, llegamos a la última parte! Vamos a resolver la tercera parte del simulacro de la guía EXANI II de Pensamiento Matemático Versión 2, desde el reactivo 21 hasta el 30.

Puedes continuar estudiando el resto de módulos y asignaturas para tu examen de ingreso con los materiales EXANI II que hemos diseñado para ti.
Reactivo 21
Suponga un sistema de 3 ecuaciones con tres incógnitas. Si cada ecuación representa un plano en el espacio y la intersección de los 3 es una misma recta, se puede concluir que:
- El sistema de ecuaciones es consistente independiente
- El sistema de ecuaciones es inconsistente
- El sistema de ecuaciones es consistente dependiente
Solución:
Lo primero que podemos asegurar, observando los tres incisos y el enunciado, es que el SE posee solución, por tanto, no puede ser inconsistente. En base a esto, descartamos la opción b).
Debemos definir si el sistema es consistente independiente o dependiente. Independiente significa que el SE posee una única solución, pero, ya que el enunciado nos dice que la solución es una recta, sobre una recta existen infinitos puntos, es decir, infinitas soluciones.
Concluimos entonces que el sistema no es independiente sino dependiente. Escogemos como correcta a la opción c).
Reactivo 22
En base a que \mathrm{c}\mathrm{o}\mathrm{s}\beta =\frac{\sqrt{7}}{4} , determine el valor de \mathrm{cot}\beta a partir del resultado mostrado.
- \frac{1}{\sqrt{7}}
- \frac{3}{4}
- \frac{\sqrt{7}}{3}
Solución:
Para encontrar la solución al problema, debemos emplear identidades trigonométricas conocidas. Comencemos indicando que la cotangente es igual al cociente entre el coseno y el seno del ángulo.
\mathrm{cot}\beta =\frac{\mathrm{cos}\beta }{\mathrm{sin}\beta }
Convertimos el \frac{1}{\mathrm{sin}\beta } en cosecante y sustituimos.
\mathrm{cot}\beta =\mathrm{cos}\beta \mathrm{csc}\beta
Empleamos la identidad pitagórica en términos de la cosecante y la cotangente.
{\mathrm{csc}}^{2}\beta =1+{\mathrm{cot}}^{2}\beta
Elevamos al cuadrado toda la primera expresión.
{\mathrm{cot}}^{2}\beta ={\mathrm{cos}}^{2}\beta {\mathrm{csc}}^{2}\beta
Sustituimos {\mathrm{csc}}^{2}\beta =1+{\mathrm{cot}}^{2}\beta
{\mathrm{cot}}^{2}\beta ={\mathrm{cos}}^{2}\beta \left(1+{\mathrm{cot}}^{2}\beta \right)
Despejamos a cotangente.
{\mathrm{cot}}^{2}\beta =\frac{{\mathrm{cos}}^{2}\beta }{1-{\mathrm{cos}}^{2}\beta }
Sustituimos el valor numérico de \mathrm{cos}\beta
{\mathrm{cot}}^{2}\beta =\frac{{\left(\surd 7/4\right)}^{2}}{1-{\left(\surd 7/4\right)}^{2}}=\frac{7}{9}
Aplicamos la raíz cuadrada de ambos lados y tomamos la parte positiva.
\mathrm{cot}\beta =\sqrt{\frac{7}{9}}=\frac{\sqrt{7}}{3}
Comparando con las opciones, concluimos que la respuesta correcta es la c).
Reactivo 23
Para permitir que la lluvia se escurra hacia los canales de drenaje urbano, las carreteras se construyen transversalmente como una parábola. Suponga que es el ingeniero encargado de diseñar unas vías urbanas próximas a ser implementadas, si el ancho del carril es de 9 metros y el punto más alto de la misma es de 0.12 m, ¿cuál es la ecuación de la parábola?
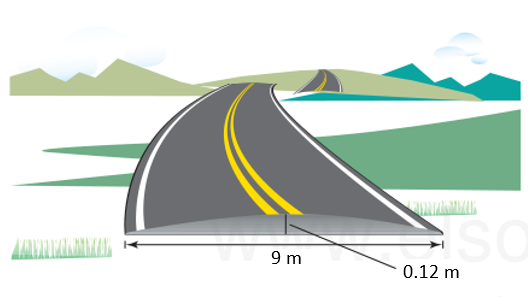
Para la construcción de la ecuación, suponga que el origen de coordenadas está a la mitad del carril.
- {x}^{2}-3=0.12y
- {y}^{2}+y-5=0.12x
- 4{x}^{2}=27\left(3-25y\right)
Solución:
Para construir la gráfica de la parábola que modela a la carretera, debemos dibujar un plano coordenado e identificar sobre él los puntos de intersección sacados de la imagen.
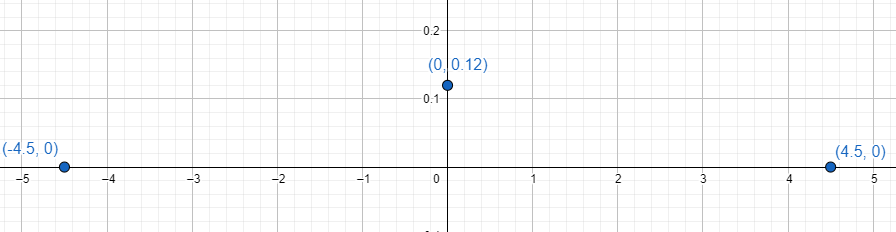
Un extremo queda a -4.5 en x , el otro a 4.5 en x y el vértice queda a 0.12 sobre el eje y . Recordemos la ecuación de una parábola que se abre verticalmente.
{\left(x-h\right)}^{2}=4p\left(y-k\right)
El vértice ya lo conocemos:
V\left(0, 0.12\right)
Sustituimos.
{x}^{2}=4p\left(y-0.12\right)
Para determinar a p sustituimos uno de los puntos conocido, en este caso será \left(-4.5, 0\right) .
{\left(-4.5\right)}^{2}=4p\left(-0.12\right)
Despejamos a 4p .
4p=\frac{{4.5}^{2}}{-0.12}=-\frac{675}{4}
Sustituimos y simplificamos.
{x}^{2}=-\frac{675}{4}\left(y-0.12\right)
4{x}^{2}=675\left(\frac{3}{25}-y\right)
4{x}^{2}=\frac{675}{25}\left(3-25y\right)
4{x}^{2}=27\left(3-25y\right)
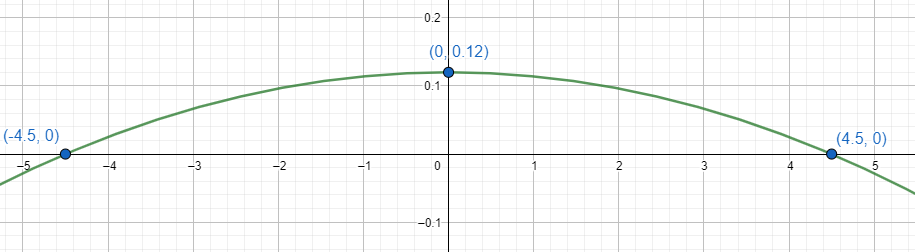
Concluimos indicando como correcta la opción c).
Reactivo 24
¿De qué forma se deben colocar signos de suma (+) y resta (-) para obtener como resultado 50?
123451- -1+2+3+45+1
- 12+3-4+5-1
- 1+2+3+4+5+1
Solución:
En este problema solo debemos aplicar algo de razonamiento para colocar correctamente los signos de suma y resta.
Si dejamos a los dígitos 4 y 5 formando un mismo número y sumamos al 2 con el 3, el resultado será 45. Por último, debemos restar un 1 para que se anule con el otro.
-1+2+3+45+1=50
Concluimos que la respuesta correcta es la a).
Reactivo 25
A partir del siguiente gráfico circular, determine cual representaría en un histograma la barra con el mayor número de solicitudes de reclamo por mes de los usuarios a una empresa de viajes, teniendo en cuenta que el gráfico se ha construido con los primeros 6 meses del año.
- Tercer mes
- Cuarto mes
- Segundo mes
Solución:
Como en cualquier gráfico en estadística, las porciones, barras, líneas o niveles, corresponden comúnmente a una cantidad o una frecuencia de un subconjunto de la muestra del experimento. Por tanto, la porción más grande en el gráfico de pastel será también la barra más grande en un histograma.
Teniendo en cuenta lo anterior, concluimos que la respuesta correcta es la opción c): el segundo mes.
Reactivo 26
La temperatura registrada cada 2 horas desde la medianoche hasta el mediodía en Mexicali, el 20 de abril del 2007, se encuentran representadas en la siguiente tabla.

Identifique el tipo de función que describe al conjunto de datos y su respectiva ecuación.
- T=38-\frac{{\left(H-3\right)}^{2}}{3}
- T=35-\frac{{\left(H-3\right)}^{2}}{3}
- T=40+\frac{{\left(H-2\right)}^{2}}{3}
Solución:
Para resolver este problema, debemos primero graficar los puntos e identificar el tipo de curva que representan.
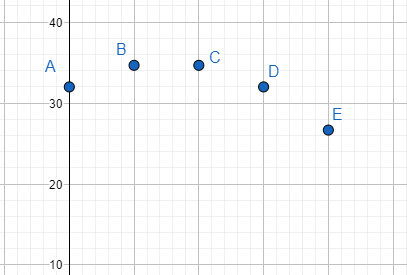
Claramente es una parábola con eje focal vertical. Si las x son las horas H y las y son la temperatura T , la ecuación de la parábola es:
{\left(H-h\right)}^{2}=4p\left(T-k\right)
Para encontrar los valores de h , k y p , debemos emplear inteligentemente los conceptos básicos de la para evitar caer en procedimientos demasiado largos. Si observamos un momento los puntos
{P}_{1}\left(\mathrm{0,32}\right);{P}_{2}\left(2,\frac{104}{3}\right);{P}_{3}\left(4,\frac{104}{3}\right);{P}_{4}\left(6, 32\right);{P}_{5}\left(8,\frac{80}{3}\right)
Los puntos {P}_{2} y {P}_{3} son simétricos, lo mismo pasa con {P}_{1} y {P}_{4} . A partir de cualquiera de los pares podemos obtener la coordenada en x del vértice como la media del segmento que forman {P}_{2} y {P}_{3} o {P}_{1} y {P}_{4} .
{x}_{v}=\frac{{p}_{2x}+{p}_{3x}}{2}=\frac{2+4}{2}=3
Sustituimos.
{\left(H-3\right)}^{2}=4p\left(T-k\right)
Ahora, debemos armar un sistema de dos ecuaciones con dos incógnitas, para ello, empleamos dos puntos que pertenezcan a la parábola. Escogemos a {P}_{1}\left(\mathrm{0,32}\right) y a {P}_{2}\left(2,\frac{104}{3}\right) .
Sustituimos {P}_{1} .
{\left(0-3\right)}^{2}=4p\left(32-k\right)
\therefore 4p=\frac{9}{32-k}
Sustituimos {P}_{2} .
{\left(2-3\right)}^{2}=4p\left(\frac{104}{3}-k\right)
\therefore 4p=\frac{3}{104-3k}
Igualamos ambas ecuaciones.
\frac{9}{32-k}=\frac{3}{104-3k}\to 32-k=3\left(104-3k\right)
9k-k=312-32\to k=35
Calculamos 4p sustituyendo en cualquiera de los despejes.
4p=\frac{3}{104-3\left(35\right)}=-3
Finalmente, la sustituimos en la ecuación de la parábola.
{\left(H-3\right)}^{2}=-3\left(T-35\right)
Desarrollamos.
T=35-\frac{{\left(H-3\right)}^{2}}{3}
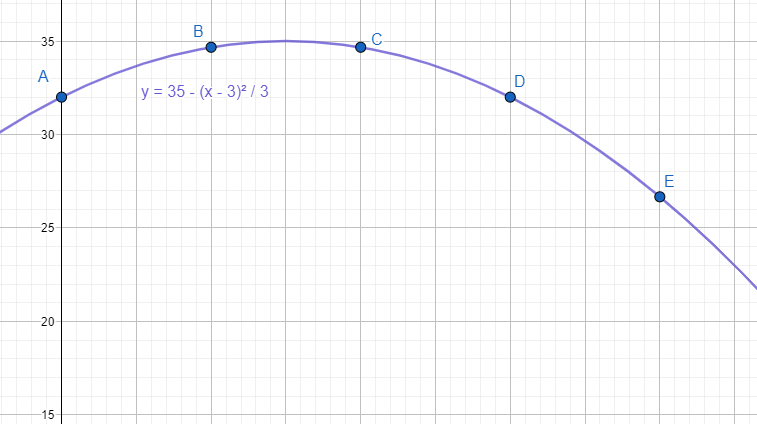
Comparando con las opciones, la respuesta correcta es la b).
Reactivo 27
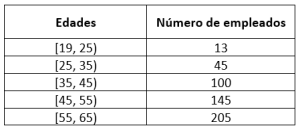
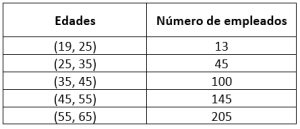
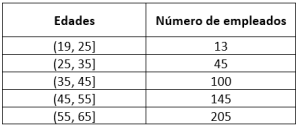
Se han recolectado las edades de los trabajadores en una planta procesadora de alimentos y se han tabulado de la siguiente manera.
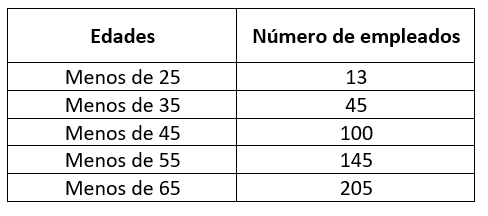
Una vez transferidos al departamento de recursos humanos, se le encomienda a usted, pasante en dicha área, reordenar los datos por intervalos. ¿Cuál de las siguientes opciones es correcta si la edad del empleado más joven es 19 años?
Solución:
Teniendo en cuenta que el empleado más joven tiene 19 años y que entre todos, no hay ninguno con edad igual o mayor a 65 años, podemos construir los intervalos de la siguiente manera:
\left[\mathrm{19,25}\right)
\left[25, 35\right)
\left[\mathrm{35,45}\right)
\left[45, 55\right)
\left[55, 65\right)
Ahora, procedemos a ordenarlos todos en una tabla como se muestra a continuación.
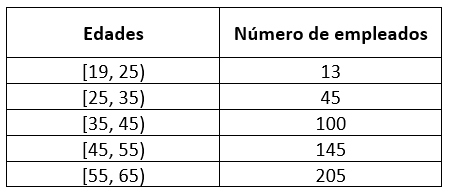
Comparando con las opciones, indicamos como correcta a la a).
Reactivo 28
¿Cuánto debe valer c en la parábola con ecuación 3{x}^{2}-2x+c , para que el vértice de la misma se encuentre en el primer cuadrante del plano cartesiano?
Ayuda: la ecuación del vértice de una parábola con eje focal paralelo al eje de las y es
V\left(\frac{-b}{2a},-\frac{{b}^{2}-4ac}{4a}\right)
- C=\frac{1}{3}
- C>\frac{1}{3}
- C<\frac{1}{3}
Solución:
En este ejercicio debemos aplicar algo de álgebra con el polinomio y con la ecuación del vértice dado. A partir de los coeficientes del polinomio, sabemos que: a=3 , b=-2 y c es desconocido. Si sustituimos a y b en la coordenada x del vértice, obtenemos:
{v}_{x}=\frac{-\left(-2\right)}{2\left(3\right)}=\frac{1}{3}
Por tanto, la única condición que queda para que el vértice esté en el primer cuadrante, es que la coordenada en y del mismo sea positiva.
-\frac{{b}^{2}-4ac}{4a}>0
Sustituimos los valores de a y b .
-\frac{{\left(-2\right)}^{2}-4\left(3\right)c}{4\left(3\right)}>0
Resolvemos la inecuación.
\frac{4-12c}{12}<0
4-12c<0\to -12c<-4
c>\frac{4}{12}
\therefore c>\frac{1}{3}
Comparando con las opciones, seleccionamos como correcta la b).
Reactivo 29
El equipo de baloncesto de una secundaria necesita escoger a su nuevo capitán antes de jugar la copa estatal de invierno. Para ello, se han tomado los datos de los 3 mejores jugadores del equipo, de los cuales, se evaluará: número de tiros acertados por partido, número de asistencias por partido y número de pases bloqueados por partido.
Tabla con el promedio de los 3 jugadores.

Se escogerá como capitán al jugador que tenga el mayor promedio en al menos 2 de los 3 aspectos mencionados anteriormente.
- Juan
- Luis
- Sebastián
Solución:
Este problema consiste en comparar los promedios de la tabla suministrada por el enunciado para realizar la selección del nuevo capitán. Iremos columna a columna indicando al mejor en dicho aspecto y el que sobresale en al menos 2, se queda con el puesto.
Tiros acertados.
Luis
Asistencias.
Sebastián.
Pases bloqueados.
Sebastián.
El nuevo capitán del equipo es Sebastián. Respuesta correcta: c).
Reactivo 30
En una empresa farmacéutica, los salarios de los trabajadores varían en base al cargo que desempeñan y se encuentran anclados al salario más bajo. Si el salario más bajo lo denotamos como SMB , en la siguiente tabla se muestra el sueldo de cada trabajador.
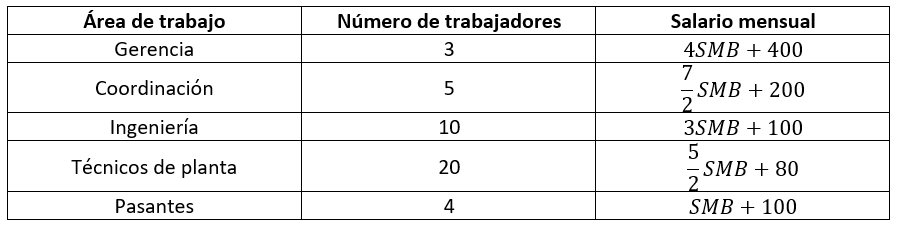
Calcule cuánto debe ser el valor del salario más bajo, para que el promedio del salario de todos los trabajadores sea, al menos, de 4500$.
- SMB>1620
- SMB\ge 1620
- SMB<10000
Solución:
Para resolver este problema, tenemos que partir del cálculo del promedio de todos los trabajadores, para lo cual, necesitamos el total de trabajadores y el sueldo de cada trabajador. Esto lo obtenemos fácilmente de la tabla.
Total de trabajadores.
n=3+5+10+20+4=42
El salario de los trabajadores lo obtenemos al multiplicar la segunda columna por su correspondiente casilla en la tercera. La suma de todo esto es el salario total. Ordenamos todo en la ecuación del promedio.
\frac{3\left(4SMB+400\right)+5\left(\frac{7}{2}SMB+200\right)+10\left(3SMB+100\right)+20\left(\frac{5}{2}SMB+80\right)+4\left(SMB+100\right)}{42}
Simplificamos la expresión.
\frac{113.5SMB+5200}{42}
Esto debe ser mayor o igual que 4500$.
\frac{113.5SMB+5200}{42}\ge 4500
Despejamos.
SMB\ge 1620\$
El salario más bajo en la farmacéutica debe ser de al menos 1620 pesos. La respuesta correcta es la b).