¡Hola aspirante! Iniciamos la solución de la segunda versión del examen simulador de pensamiento matemático con temas oficiales de la nueva Guía EXANI II.

Resolveremos la primera parte, que va desde el reactivo 1 hasta el 10, y después vamos con los ejercicios del 11 al 30, ¿va?.
Este examen simulador tiene como objetivo que practiques e identifiques los temas que más se te compliquen, recuerda que para obtener un buen resultado en tu examen de admisión debes practicar, y estudiar la teoría correspondiente a cada tema.
Te recomiendo repasar el temario de pensamiento matemático antes de iniciar con los ejercicios.
Estructura del EXANI II
La prueba de ingreso está dividida en dos grandes partes: habilidades y conocimientos y los módulos específicos.
Algunas universidades aplican una prueba diagnóstica de inglés, que no cuenta para la calificación final. Debes consultar esta información en la convocatoria de tu universidad.
Examen de habilidades y conocimientos
La parte habilidades y conocimientos se aplica en todas las carreras y consta de 90 reactivos: 60 de Español y 30 de Matemáticas. Te dejo la distribución de los reactivos del EXANI II en la siguiente tabla.
Estructura del examen y la guía del EXANI II
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Conocimientos específicos
Esta segunda parte posee un total de 15 módulos. Todos los estudiantes deben responder 2 módulos en su examen de ingreso, los cuales varían de acuerdo con la carrera.
Es necesario que revises la convocatoria de tu universidad para conocer los módulos van para tu examen. La siguiente es una lista con los módulos específicos del EXANI II.
| 1. Administración | 9. Física |
| 2. Aritmética | 10. Historia |
| 3. Biología | 11. Literatura |
| 4. Cálculo diferencial e integral | 12. Matemáticas financieras |
| 5. Ciencias de la Salud | 13. Premedicina |
| 6. Derecho | 14. Probabilidad y estadística |
| 7. Economía | 15. Química |
| 8. Filosofía | 16. Psicología |
Temario Pensamiento Matemático EXANI II
A continuación tienes la distribución de los 30 reactivos de pensamiento matemático en los temas que van para el examen.
| Contenido | Reactivos |
|---|---|
| Herramientas Algebraicas: Resolución de problemas mediante el empleo de ecuaciones y sistemas lineales, ya sea a través de la representación de cantidades o de la representación gráfica | 10 |
| Problemas, Probabilidad y Análisis de Datos: Creación y análisis de relaciones, representación y análisis de datos cuantitativos y aplicación de probabilidades | 15 |
| Matemáticas Avanzadas: Creación de expresiones algebraicas y uso de gráficos que representan funciones exponenciales no lineales o cuadráticas | 15 |
| Temas Adicionales en Matemáticas: Solución de problemas asociados al área y volumen, aplicación de definiciones, teoremas sobre líneas, ángulos, triángulos y círculos | 10 |
| Total | 50 |
Recomendaciones para resolver la guía
- Elimina las distracciones. Ve a un sitio en el que te sientas cómodo o cómoda, coloca tu teléfono en modo avión y mantén cerca de ti lapiceros, borrador y libretas.
- No te enfoques en el resultado, sino en el procedimiento. Coloca toda tu atención en analizar y desglosar los problemas para identificar las herramientas que debes usar. Una buena estrategia conlleva a buenos resultados.
- Lleva el tiempo mientras resuelves la guía. Mide el tiempo durante cada sesión de estudios, buscando acortar el tiempo lo más que puedas antes del examen.
- Si un reactivo parece demasiado difícil, ve al siguiente. Evita caer en frustración mientras estudias, mantener el foco y meditar esos ejercicios difíciles, te permitirán desarrollar capacidades analíticas sólidas.
Reactivo 1
Un alpinista desea medir la altura de una gran montaña, pero la única información que posee sobre la misma, es que cuando mira hacia la cima desde el punto P y el ángulo es \alpha y cuando lo hace desde el punto Q el ángulo es \beta . Teniendo en cuenta que \beta >\alpha , ¿Cuál es la expresión que permite calcular la altura de la montaña?
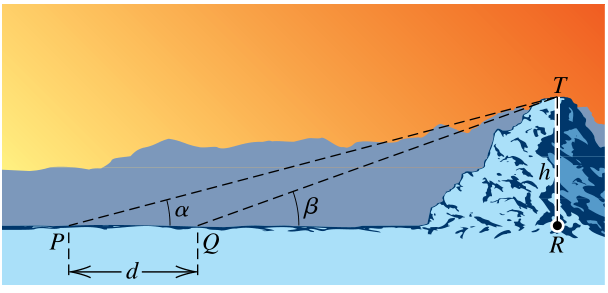
- h=\frac{d}{\mathrm{c}\mathrm{o}\mathrm{t}\alpha -\mathrm{c}\mathrm{o}\mathrm{t}\beta }
- h=\frac{d}{\mathrm{t}\mathrm{g}\alpha -\mathrm{t}\mathrm{g}\beta }
- h=\frac{d}{\mathrm{s}\mathrm{e}\mathrm{n}\alpha -\mathrm{s}\mathrm{e}\mathrm{n}\beta }
Solución:
Para resolver este problema, debemos aplicar trigonometría con los conjuntos de datos ofrecidos por el problema, luego debemos igualar en ambos triángulos la altura de la montaña RT=h y despejar. El resultado debe quedar en función de \beta , \alpha y d .
Primer triángulo PTR .
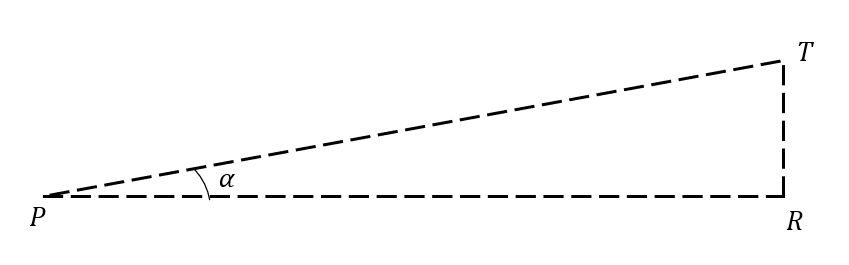
Nos interesa una ecuación que relaciona al ángulo, la altura RT y el cateto adyacente PR , de tal forma que luego hagamos la resta PR-QR=d y así despejar a h . Emplearemos la identidad de la tangente de alfa.
\mathrm{tan}\alpha =\frac{h}{PR}\to PR=\frac{h}{\mathrm{tan}\alpha }
Segundo triángulo QTR .
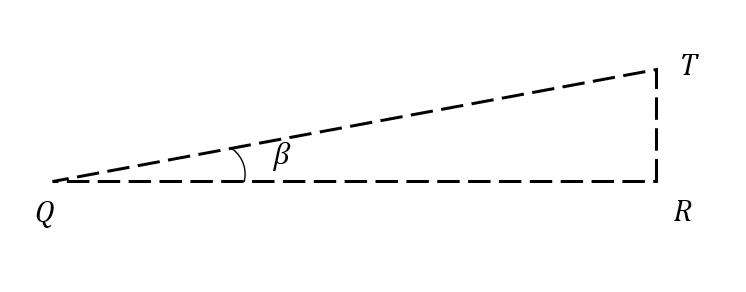
De la misma manera, empleamos la relación trigonométrica de la tangente en el triángulo QTR y despejamos a QR .
\mathrm{tan}\beta =\frac{h}{QR}\to QR=\frac{h}{\mathrm{tan}\beta }
Ahora, restamos los catetos adyacentes de ambos triángulos.
PR-QR=\frac{h}{\mathrm{tan}\alpha }-\frac{h}{\mathrm{tan}\beta }=d
h\left(\frac{1}{\mathrm{tan}\alpha }-\frac{1}{\mathrm{tan}\beta }\right)=d\to h\left(\mathrm{cot}\alpha -\mathrm{cot}\beta \right)=d
\therefore h=\frac{d}{\mathrm{cot}\alpha -\mathrm{cot}\beta }
Finalmente, comparamos con las opciones y concluimos que la correcta es la a).
Reactivo 2
Calcule el valor del área que se encuentra sombreada, teniendo en cuenta que el cuadrado tiene lado igual a 1 unidad y que las figuras curvas son secciones circulares rectas centradas en el cuadrado.

- \frac{6}{8}-2\pi
- 7-\pi
- \frac{6-\pi }{8}
Solución:
Como en todos los ejercicios de encontrar el área sombreada, primero debemos identificar figuras conocidas en la región de color blanco, calcular sus áreas de forma individual, sumarlas y luego restarle el total al área del cuadrado. Iniciamos identificando figuras conocidas en la zona blanca.
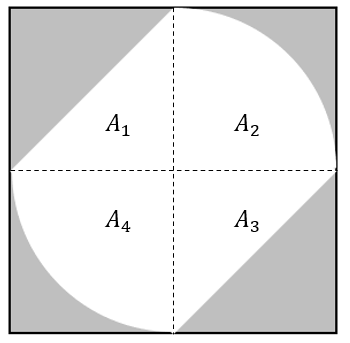
El área de la región blanca es:
{A}_{b}={A}_{1}+{A}_{2}+{A}_{3}+{A}_{4}
Además, {A}_{1} y {A}_{3} son triángulos rectángulos mientras que {A}_{2} y {A}_{4} son cuartos de círculos. Recordemos que la región blanca toca al cuadrado en los puntos medios de sus aristas.
{A}_{b}=\frac{{b}_{1}{h}_{1}}{2}+\frac{\pi {r}_{2}^{2}}{4}+\frac{{b}_{3}{h}_{3}}{2}+\frac{\pi {r}_{4}^{2}}{4}
Examinando la imagen, sabemos que:
{b}_{1}={b}_{3}=\frac{1}{2}
{h}_{1}={h}_{3}=\frac{1}{2}
{r}_{2}={r}_{4}=\frac{1}{2}
Sustituyendo nos queda:
{A}_{b}=\frac{\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)}{2}+\frac{\pi {\left(\frac{1}{2}\right)}^{2}}{4}+\frac{\left(\frac{1}{2}\right)\left(\frac{1}{2}\right)}{2}+\frac{\pi {\left(\frac{1}{2}\right)}^{2}}{4}=\frac{1}{8}+\frac{\pi }{16}+\frac{1}{8}+\frac{\pi }{16}
{A}_{b}=\frac{1}{4}+\frac{\pi }{8}
Procedemos a restar el área blanca al área del cuadrado.
{A}_{s}={A}_{c}-{A}_{b}=1-\frac{1}{4}-\frac{\pi }{8}=\frac{3}{4}-\frac{\pi }{8}
\therefore {A}_{s}=\frac{6-\pi }{8}
Comparando con los incisos, la respuesta correcta está en c).
Reactivo 3
Resuelva el siguiente producto de polinomios:
\left(3x+5\right)\left(2{x}^{2}+9x-5\right)
- 6{x}^{3}+37{x}^{2}+30x-25
- {x}^{2}(3x+5)
- 16{x}^{4}-2{x}^{2}-5
Solución:
Para encontrar el producto de ambos polinomios, debemos seleccionar el que tenga la menor cantidad de términos y multiplicar, cada uno de ellos, por el otro polinomio. En este caso, el que tiene menos términos es 3x+5 , por tanto, ejecutamos la distributiva término a término con 2{x}^{2}+9x-5 .
\left(3x+5\right)\left(2{x}^{2}+9x-5\right)=3x\left(2{x}^{2}+9x-5\right)+5\left(2{x}^{2}+9x-5\right)
Resolvemos los paréntesis.
3x\left(2{x}^{2}+9x-5\right)+5\left(2{x}^{2}+9x-5\right)=6{x}^{3}+27{x}^{2}-15x+10{x}^{2}+45x-25
Sumamos o restamos términos semejantes.
6{x}^{3}+27{x}^{2}-15x+10{x}^{2}+45x-25=6{x}^{3}+37{x}^{2}+30x-25
Comparando con las opciones del problema, la respuesta correcta es la a).
Reactivo 4
En una fábrica de colchones, se ha estimado que el material en la planta de acolchado x más 4 debe ser mayor o igual que 1.2 veces la producción de unidades diarias sumado 5. Si la producción diaria es de 30 unidades, determine:
- La inecuación que describe la situación
- La cantidad de material x en la planta
- x+4\ge 41 , x\ge 30
- x-4\ge 41 , x\ge 37
- x+4\ge 41, x\ge 37
Solución:
Para encontrar la inecuación que describe la situación y, posteriormente, el intervalo solicitado, debemos analizar la frase en lenguaje natural para escribirla en lenguaje algebraico. La primera parte indica:
…el material en la planta de acolchado x más 4 debe ser mayor o igual que 1.2 veces la producción de unidades diarias sumado 5…
Esto se puede escribir como:
x+4\ge 1.2PD+5
Donde PD es la producción diaria, que luego se indica que es igual a 30. Sustituimos.
x+4\ge 1.2\left(30\right)+5
x+4\ge 41
Ahora, solo nos queda despejar a x para encontrar el conjunto solución.
x+4\ge 41\to x\ge 41-4
\therefore x\ge 37
Finalmente:
x+4\ge 41, x\ge 37
Comparando con las opciones, la respuesta correcta está en la c).
Reactivo 5
Las funciones de oferta, demanda y tendencia de compra corresponden a líneas rectas que se grafican en un plano coordenado cuyas variables son el precio P y la cantidad del producto Q . En base a la lógica de mercado, ¿Cuál de las siguientes aseveraciones es correcta?
- El precio de un producto sube si incrementa la oferta
- La tendencia de compra y la demanda tienen pendiente positiva
- El punto de equilibrio de mercado se encuentra en el origen del sistema coordenado
Solución:
En este problema, debemos analizar una a una las aseveraciones que se encuentran en los incisos. Por parte de la frase a), queda claro que es incorrecta, porque a medida que mayor cantidad de un producto existe en el mercado, el precio tiende a caer.
La segunda es cierta. Pensemos en que la demanda y la tendencia de compra tienen relación directa con el ritmo de compra de un producto, a medida que más personas quieren un producto, este naturalmente incrementa de precio, por tanto, las pendientes de ambos modelos deben ser positivas.
La última se refiere a un absurdo, ya que, por definición, el punto de equilibrio es la intersección de las curvas de oferta, demanda y tendencia de compra, que no ocurre en el origen de coordenadas. Concluimos finalmente que la respuesta correcta está en la b).
Reactivo 6
Un estudiante de una universidad dedica al estudio, en horas, durante la semana el siguiente tiempo:
3.5, 5, 4, 6, 5.5, 5
Calcule el rango, la varianza y la desviación típica de los datos suministrados.
- rango=2.5;varianza=0.72;desviación típica=0.85
- rango=4;varianza=2.16;desviación típica=0.08
- rango=3;varianza=6.16;desviación típica=11.08
Solución:
Los tres parámetros estadísticos solicitados por el problema, corresponden a medidas de desviación. A continuación, se presentan las ecuaciones para el cálculo de cada una de ellas.
Rango.
r=Max-Min
Varianza.
{s}^{2}=\frac{\sum _{1}^{n} {\left({x}_{i}-\stackrel{-}{X}\right)}^{2}}{n}
Desviación estándar.
s=\sqrt{\frac{\sum _{1}^{n} {\left({x}_{i}-\stackrel{-}{X}\right)}^{2}}{n}}
Comenzamos ordenando las cantidades de forma ascendente.
3.5, 4, 5, 5, 5.5, 6
Para el rango, escogemos el límite superior 6 y el límite inferior 3.5:
r=6-3.5=2.5
Para la varianza, calculamos primero la media:
\stackrel{-}{x}=\frac{3.5+4+5+5+5.5+6}{6}=4.83
Ahora, calculamos {\left({x}_{i}-\stackrel{-}{X}\right)}^{2} .
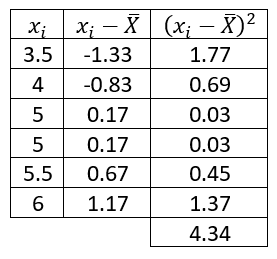
Sustituimos en la ecuación.
{s}^{2}=\frac{1.77+0.69+0.03+0.03+0.45+1.37}{6}=\frac{4.34}{6}=0.72
La desviación estándar se calcula como la raíz cuadrada de la varianza, por tanto:
s=\sqrt{0.72}=0.85
Comparando con las opciones, la respuesta correcta es la a).
Reactivo 7
En la siguiente tabla se encuentran expresados el número de nacidos en una unidad médica durante los primeros 6 días del año.

Calcule la media de los datos recolectados.
- 50
- 33
- 3
Solución:
La media aritmética de un conjunto de datos no agrupados se determina como la suma de los datos, dividida entre la cantidad de datos. En este caso, la cantidad de datos n=6 .
\stackrel{-}{x}=\frac{12+34+46+24+2+4}{6}=\frac{122}{6}=20.3
Concluimos que la respuesta correcta es la c).
Reactivo 8
Determine el valor de x , para que se cumpla que \frac{y}{x}=2 .
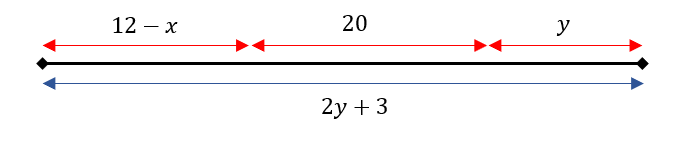
- 1
- \frac{29}{3}
- 88
Solución:
En este caso, debemos buscar un sistema de ecuaciones para calcular el valor indicado. Primero, sabemos que todo el segmento 2y+3 es igual a la suma de los tres segmentos contenidos en él.
2y+3=12-x+20+y
2y+3=32-x+y
x+y=29
Del enunciado, sabemos que \frac{y}{x}=2 , despejando a y tenemos:
y=2x
Sustituimos.
x+2x=29\to 3x=29
x=\frac{29}{3}
Comparando con las opciones, la respuesta correcta es la b).
Reactivo 9
Una colonia de bacterias fue atacada con un antibiótico de alta concentración con la finalidad de comprobar la resistencia de dicha colonia al medicamento. El resultado final, luego de un extenuante conteo bajo el microscopio, reveló que el 83% de las bacterias soportaron el medicamento y el resto pereció.
Si se sabe que la colonia era de aproximadamente 3500 bacterias, indique el número de afectadas por cada 100 bacterias.
- 22
- 500
- 17
Solución:
En este caso, debemos calcular la cantidad de bacterias afectadas respecto de extraer una muestra de 100, es decir, debemos llevar el total de bacterias enfermas medidas en la población de 3500 a una muestra de 100.
Primero calculamos la cantidad de bacterias afectadas.
{b}_{a}=\left(1-0.83\right)*3500=595
Ahora, aplicamos una sencilla regla de tres.
Si en 3500 hay 595 enfermas, ¿cuántas enfermas habrá si solo tomo 100?
3500\to 595
100\to x
x=100*\frac{595}{3500}=17
Concluimos entonces que la respuesta correcta es la c).
Reactivo 10
El siguiente grafo representa un conjunto de ciudades conectadas por caminos. Cada ciudad se encuentra identificada con una letra y cada flecha indica el sentido de circulación y la distancia que mide.
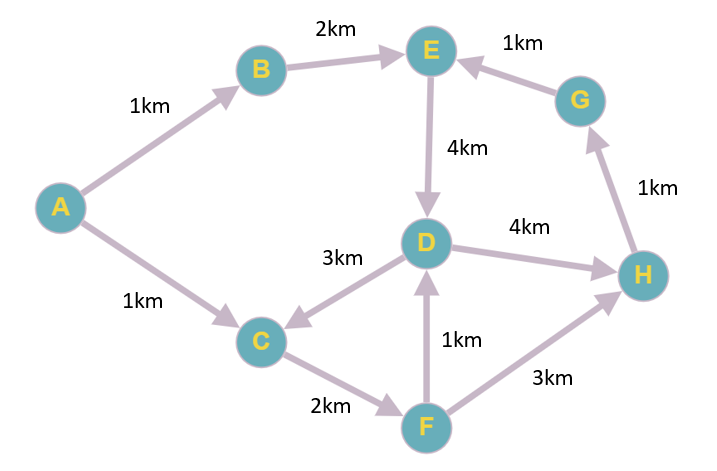
- ABEDH
- ACDH
- ACFH
Solución:
En este caso, solo debemos seguir el sentido de las flechas, considerando cuánto mide cada una para obtener el camino más corto. Desde el nodo A solo podemos tomar dos caminos, hacia B o hacia C.
Si tomamos el camino hacia B, tendremos que ir hacia E, luego hacia D y finalmente hacia H. Esto da un total de 1+2+4+4=11 \mathrm{k}\mathrm{m} . En el caso de ir por C, debemos seguir hacia F y luego hacia H, lo que da un total de 1+2+3=6 \mathrm{k}\mathrm{m} , por lo tanto, el camino más corto es ACFH.
La respuesta correcta es el inciso c).


