¡Llegamos a la última parte, aspirante! En este tutorial resolveremos la quinta parte del examen simulacro para la guía EXANI II de Cálculo diferencial e integral, desde el reactivo 41 hasta el 50.

Recuerda desarrollarlos por tu cuenta antes de revisar la solución.
Puedes continuar estudiando para tu examen de ingreso con los materiales EXANI II que tenemos para ti.
Reactivo 41
Relacione la integral con la sustitución trigonométrica que permite resolverla.

- 1a, 2c, 3b
- 1c, 2a, 3b
- 1b, 2c, 3a
Solución:
El método de integración por sustitución trigonométrica, consiste en armar un triángulo rectángulo con los elementos que conforman una expresión matemática similar al teorema de Pitágoras.
A partir de esto, se deducen 3 posibles cambios de variable:

Teniendo esto como referencia, podemos ir relacionando el cambio de la columna derecha con la integral en la columna izquierda.
Primera integral.
\int \frac{dx}{{\left(4-{x}^{2}\right)}^{3/2}}=\int \frac{dx}{{\left({2}^{2}-{x}^{2}\right)}^{3/2}}
Examinando la imagen, corresponde al primer caso.
x=2\mathrm{sin}\theta
1a.
Segunda integral.
\int \frac{{x}^{2}}{\sqrt{{x}^{2}-16}}dx=\int \frac{{x}^{2}}{\sqrt{{x}^{2}-{4}^{2}}}dx
Corresponde al segundo caso.
x=4\mathrm{sec}\theta
2c.
Por descartes: 3b. Uniendo todas las respuestas parciales nos queda: 1a, 2c, 3b.
La respuesta correcta es el inciso a).
Reactivo 42
Aplicando el método de integración fracciones parciales, encuentre la solución a la siguiente integral.
\int \frac{{x}^{3}+1}{{x}^{4}-{x}^{3}}dx
- I=-\mathrm{ln}\left|x\right|+\frac{1}{x}+\frac{1}{2{x}^{2}}+2\mathrm{ln}\left|x-1\right|+C
- I=-\mathrm{ln}\left|x\right|+\frac{1}{x}+\frac{1}{2{x}^{2}}+C
- I=-\frac{1}{x}+\frac{1}{2{x}^{2}}+2\mathrm{ln}\left|x-1\right|+C
Solución:
Antes de separar en fracciones parciales, vamos a extraer factor común {x}^{3} en el denominador.
\int \frac{{x}^{3}+1}{{x}^{4}-{x}^{3}}dx=\int \frac{{x}^{3}+1}{{x}^{3}\left(x-1\right)}dx
Procedemos a separar en fracciones parciales, teniendo en cuenta que la triple potencia de x se descompone en 3 fracciones.
\frac{{x}^{3}+1}{{x}^{3}\left(x-1\right)}=\frac{{a}_{1}}{x}+\frac{{a}_{2}}{{x}^{2}}+\frac{{a}_{3}}{{x}^{3}}+\frac{{a}_{4}}{x-1}
Pasamos a multiplicar el denominador de la izquierda hacia la derecha.
{x}^{3}+1={a}_{1}{x}^{2}\left(x-1\right)+{a}_{2}x\left(x-1\right)+{a}_{3}\left(x-1\right)+{a}_{4}{x}^{3}
Desarrollando y agrupando nos queda:
\left({a}_{1}+{a}_{4}\right){x}^{3}+\left({a}_{2}-{a}_{1}\right){x}^{2}+\left({a}_{3}-{a}_{2}\right)x-{a}_{3}={x}^{3}+1
Igualamos términos.
\begin{array}{c}\begin{array}{c}{a}_{1}+{a}_{4}=1\\ {a}_{2}-{a}_{1}=0\end{array}\\ \begin{array}{c}{a}_{3}-{a}_{2}=0\\ -{a}_{3}=1\end{array}\end{array}
Despejamos de forma directa a {a}_{3} .
{a}_{3}=-1
\begin{array}{c}{a}_{1}+{a}_{4}=1\\ {a}_{2}-{a}_{1}=0\\ -1-{a}_{2}=0\end{array}
Despejamos a {a}_{2} .
{a}_{2}=-1
Despejamos a {a}_{1} .
{a}_{1}=-1
Finalmente, obtenemos el valor de {a}_{4} .
{a}_{4}=1+1=2
Sustituimos en la descomposición en fracciones parciales.
\frac{{x}^{3}+1}{{x}^{3}\left(x-1\right)}=-\frac{1}{x}-\frac{1}{{x}^{2}}-\frac{1}{{x}^{3}}+\frac{2}{x-1}
Sustituimos en la integral.
\int \left(-\frac{1}{x}-\frac{1}{{x}^{2}}-\frac{1}{{x}^{3}}+\frac{2}{x-1}\right)dx=-\int \frac{1}{x}dx-\int \frac{1}{{x}^{2}}dx-\int \frac{1}{{x}^{3}}dx+2\int \frac{1}{x-1}dx
Integramos de forma directa aplicando la fórmula del inverso de x y de una potencia.
-\int \frac{1}{x}dx-\int \frac{1}{{x}^{2}}dx-\int \frac{1}{{x}^{3}}dx+2\int \frac{1}{x-1}dx=-\mathrm{ln}\left|x\right|+\frac{1}{x}+\frac{1}{2{x}^{2}}+2\mathrm{ln}\left|x-1\right|+C
Finalmente:
\int \frac{{x}^{3}+1}{{x}^{4}-{x}^{3}}dx=-\mathrm{ln}\left|x\right|+\frac{1}{x}+\frac{1}{2{x}^{2}}+2\mathrm{ln}\left|x-1\right|+C
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 43
Dada la integral:
\int \frac{11{x}^{2}-10x+3}{4{x}^{3}-4{x}^{2}+x}dx
¿Cuál es la separación en fracciones parciales que permite simplificar su solución?
- \frac{11{x}^{2}-10x+3}{4{x}^{3}-4{x}^{2}+x}=\frac{11{x}^{2}}{4{x}^{3}-4{x}^{2}+x}-\frac{10x}{4{x}^{3}-4{x}^{2}+x}+\frac{3}{4{x}^{3}-4{x}^{2}+x}
- \frac{11{x}^{2}-10x+3}{4{x}^{3}-4{x}^{2}+x}=\frac{11}{x}-\frac{10x}{2x-1}+\frac{3}{{\left(2x-1\right)}^{2}}
- \frac{11{x}^{2}-10x+3}{4{x}^{3}-4{x}^{2}+x}=\frac{3}{x}-\frac{1}{2\left(2x-1\right)}+\frac{3}{{2\left(2x-1\right)}^{2}}
Solución:
Extraemos factor común x del denominador y aplicamos fracciones parciales.
\frac{11{x}^{2}-10x+3}{4{x}^{3}-4{x}^{2}+x}=\frac{11{x}^{2}-10x+3}{x\left(4{x}^{2}-4x+1\right)}
Factorizamos el polinomio de segundo grado.
\frac{11{x}^{2}-10x+3}{x\left(4{x}^{2}-4x+1\right)}=\frac{11{x}^{2}-10x+3}{x{\left(2x-1\right)}^{2}}
Aplicamos fracciones parciales.
\frac{11{x}^{2}-10x+3}{x{\left(2x-1\right)}^{2}}=\frac{{a}_{1}}{x}+\frac{{a}_{2}}{2x-1}+\frac{{a}_{3}}{{\left(2x-1\right)}^{2}}
Pasamos a multiplicar el denominador de la fracción de la izquierda.
11{x}^{2}-10x+3={a}_{1}{\left(2x-1\right)}^{2}+{a}_{2}x\left(2x-1\right)+{a}_{3}x
Desarrollando y agrupando nos queda:
\left(4{a}_{1}+2{a}_{2}\right){x}^{2}+\left({a}_{3}-4{a}_{1}-{a}_{2}\right)x+{a}_{1}=11{x}^{2}-10x+3
Igualamos los coeficientes de términos semejantes.
\begin{array}{c}4{a}_{1}+2{a}_{2}=11\\ {a}_{3}-4{a}_{1}-{a}_{2}=-10\\ {a}_{1}=3\end{array}
El valor de {a}_{1} lo obtenemos de manera directa. Sustituimos el resto de expresiones.
\begin{array}{c}4\left(3\right)+2{a}_{2}=11\\ {a}_{3}-4\left(3\right)-{a}_{2}=-10\end{array}\to \begin{array}{c}12+2{a}_{2}=11\\ {a}_{3}-12-{a}_{2}=-10\end{array}\to \begin{array}{c}{a}_{2}=-\frac{1}{2}\\ {a}_{3}-{a}_{2}=2\end{array}
{a}_{3}+\frac{1}{2}=2\to {a}_{3}=\frac{3}{2}
Sustituyendo los coeficientes en la descomposición nos queda:
\frac{11{x}^{2}-10x+3}{x{\left(2x-1\right)}^{2}}=\frac{3}{x}-\frac{1}{2\left(2x-1\right)}+\frac{3}{2{\left(2x-1\right)}^{2}}
La respuesta correcta es el inciso c).
Reactivo 44
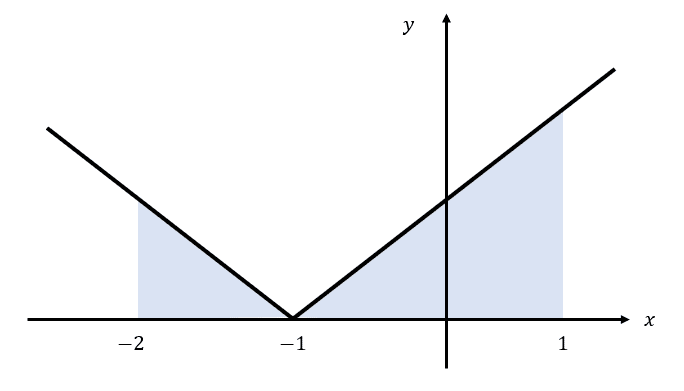
Dada la siguiente gráfica, identifique cuál de las siguientes integrales definidas representa el cálculo del área sombreada.
- {\int }_{-2}^{1}\left|x\right|dx
- {\int }_{-2}^{1}\left(x-1\right)dx
- {\int }_{-2}^{1}\left|x+1\right|dx
Solución:
La función que se muestra en la figura, corresponde a la función valor absoluto desplazada hacia el -1. Este corrimiento lo expresamos como:
f\left(x\right)=\left|x-\left(-1\right)\right|=\left|x+1\right|
Teniendo en cuenta que el intervalo de integración es \left[-2, 1\right] , la integral definida que nos entrega el área bajo la función en este intervalo es:
{\int }_{-2}^{1}\left|x+1\right|dx
Indicamos como respuesta correcta al inciso c).
Reactivo 45
¿Cuál es el área debajo de la curva y=\sqrt{x-1} en el intervalo \left[1, 4\right] ?
- I=2\sqrt{3}
- I=2
- I=\sqrt{2}
Solución:
Establecemos la integral para calcular el área bajo la curva en el intervalo dado.
{\int }_{1}^{4}\sqrt{x-1}dx
Debemos aplicar el segundo teorema fundamental del cálculo para resolver la integral definida.
{\int }_{a}^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right)
Donde F es la primitiva de f . Iniciamos integrando indefinidamente.
{\int }_{1}^{4}\sqrt{x-1}dx={\int }_{1}^{4}{\left(x-1\right)}^{1/2}dx=\left.\frac{{\left(x-1\right)}^{\frac{1}{2}+1}}{\frac{1}{2}+1}\right]\begin{array}{c}4\\ \\ 1\end{array}=\left.\frac{{2\left(x-1\right)}^{3/2}}{3}\right]\begin{array}{c}4\\ \\ 1\end{array}
Evaluamos la primitiva en los extremos.
\left.\frac{{2\left(x-1\right)}^{3/2}}{3}\right]\begin{array}{c}4\\ \\ 1\end{array}=\frac{{2\left(4-1\right)}^{3/2}}{3}-\frac{{2\left(1-1\right)}^{\frac{3}{2}}}{3}=\frac{2}{3}{3}^{\frac{3}{2}}-0=2\sqrt{3}
Finalmente:
{\int }_{1}^{4}\sqrt{x-1}dx=2\sqrt{3}\approx 3.4641
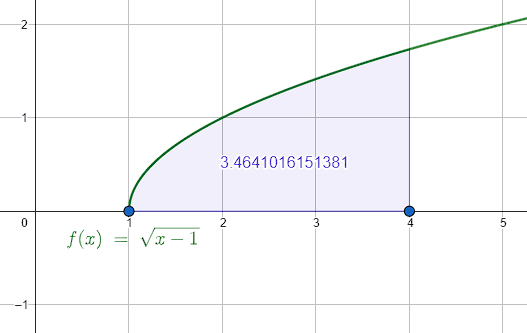
Indicamos como respuesta correcta al inciso a).
Reactivo 46
Calcule la siguiente integral definida.
{\int }_{0}^{\pi }\sqrt{2+2\mathrm{cos}\alpha }d\alpha
- I=1
- I=4
- I=-4
Solución:
Para encontrar el valor de la integral, aplicamos el segundo teorema fundamental del cálculo. Iniciamos integrando indefinidamente.
{\int }_{0}^{\pi }\sqrt{2+2\mathrm{cos}\alpha }d\alpha
Extraemos factor común al 2.
{\int }_{0}^{\pi }\sqrt{2+2\mathrm{cos}\alpha }d\alpha =\sqrt{2}{\int }_{0}^{\pi }\sqrt{1+\mathrm{cos}\alpha }d\alpha
Examinando las identidades trigonométricas, tenemos que:
\mathrm{cos}\left(\frac{\alpha }{2}\right)=\sqrt{\frac{1+\mathrm{cos}\alpha }{2}}
Despejando a la raíz nos queda:
\sqrt{1+\mathrm{cos}\alpha }=\sqrt{2}\mathrm{cos}\left(\frac{\alpha }{2}\right)
Sustituimos.
\sqrt{2}{\int }_{0}^{\pi }\sqrt{1+\mathrm{cos}\alpha }d\alpha =\sqrt{2}{\int }_{0}^{\pi }\sqrt{2}\mathrm{cos}\left(\frac{\alpha }{2}\right)d\alpha =2{\int }_{0}^{\pi }\mathrm{cos}\left(\frac{\alpha }{2}\right)d\alpha
Integramos de forma inmediata.
2{\int }_{0}^{\pi }\mathrm{cos}\left(\frac{\alpha }{2}\right)d\alpha =\left.\begin{array}{c}\\ 2\left[2\mathrm{sin}\left(\frac{\alpha }{2}\right)\right]\\ \end{array}\right]\begin{array}{c}\pi \\ \\ 0\end{array}=\left.\begin{array}{c}\\ 4\mathrm{sin}\left(\frac{\alpha }{2}\right)\\ \end{array}\right]\begin{array}{c}\pi \\ \\ 0\end{array}=4\mathrm{sin}\left(\frac{\pi }{2}\right)-4\mathrm{sin}\left(0\right)=4\left(1\right)-0
Finalmente:
{\int }_{0}^{\pi }\sqrt{2+2\mathrm{cos}\alpha }d\alpha =4
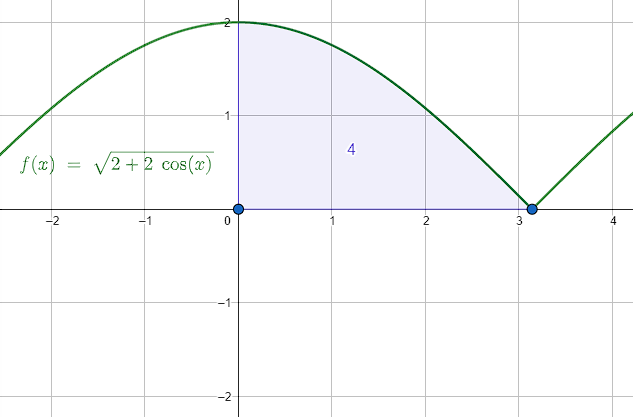
La respuesta correcta es el inciso b).
Reactivo 47
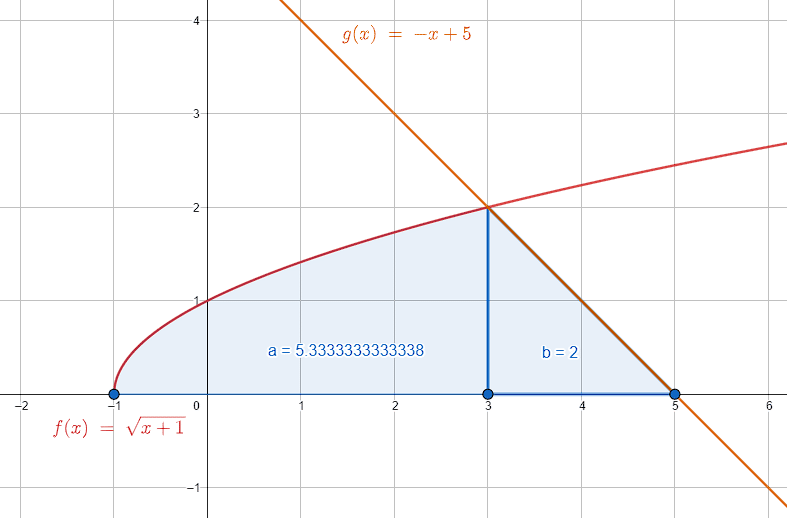
Hallar el área de la región encerrada por el eje x , la curva y=\sqrt{x+1} y la recta y=-x+5 . Tenga en cuenta que la recta y la curva se interceptan en x=3 .
- I=22
- I=\frac{22}{3}
- I=\frac{3}{22}
Solución:
Iniciamos graficando la recta y la curva.

A partir de la gráfica, vemos que desde -1 hasta 3 debemos integrar con \sqrt{x+1} , mientras que desde 3 hasta 5 es necesario utilizar la recta. El área de la región descrita por la curva la recta y el eje x se obtiene como:
A={\int }_{-1}^{3}\sqrt{x+1}dx+{\int }_{3}^{5}\left(-x+5\right)dx
En ambos casos integramos indefinidamente y luego evaluamos en los extremos.
A=\left.\frac{{2\left(x+1\right)}^{\frac{3}{2}}}{3}\right]\begin{array}{c}3\\ \\ -1\end{array}+\left.\left(-\frac{{x}^{2}}{2}+5x\right)\right]\begin{array}{c}5\\ \\ 3\end{array}
Evaluamos por separado para no hacer ilegible la solución.
{A}_{1}=\left.\frac{{2\left(x+1\right)}^{\frac{3}{2}}}{3}\right]\begin{array}{c}3\\ \\ -1\end{array}=\frac{{2\left(3+1\right)}^{\frac{3}{2}}}{3}-\frac{{2\left(-1+1\right)}^{\frac{3}{2}}}{3}=\frac{16}{3}-0=\frac{16}{3}
{A}_{2}=\left[-\frac{{5}^{2}}{2}+5\left(5\right)\right]-\left[-\frac{{3}^{2}}{2}+5\left(3\right)\right]=\frac{25}{2}-\frac{21}{2}=2
A={A}_{1}+{A}_{2}=\frac{16}{3}+2=\frac{22}{3}
La respuesta correcta es el inciso b).
Reactivo 48
Calcule la longitud de la curva plana y=\mathrm{ln}\left[\mathrm{cos}x\right] en el intervalo x\left[\frac{\pi }{6},\frac{\pi }{4}\right] .
- L=\mathrm{ln}\left(\frac{\sqrt{2}+1}{\sqrt{3}}\right)
- L=\mathrm{ln}\left(\frac{\sqrt{2}}{\sqrt{3}}\right)
- L=\mathrm{ln}\left(\frac{1}{\sqrt{3}}\right)
Solución:
Para calcular la longitud de cualquier curva, empleamos la siguiente ecuación integral.
L={\int }_{a}^{b}\sqrt{1+{\left[{f}^{\text{'}}\left(x\right)\right]}^{2}}dx
Iniciamos calculando la derivada de la función.
{f}^{\text{'}}\left(x\right)={\left[\mathrm{ln}\left(\mathrm{cos}x\right)\right]}^{\text{'}}=-\frac{\mathrm{sin}x}{\mathrm{cos}x}=-\mathrm{tan}x
Sustituimos en la expresión.
L={\int }_{\frac{\pi }{6}}^{\frac{\pi }{4}}\sqrt{1+{\mathrm{tan}x}^{2}}dx
Sustituimos 1+{\mathrm{tan}x}^{2} por {\mathrm{sec}}^{2}x mediante la identidad pitagórica.
L={\int }_{\frac{\pi }{6}}^{\frac{\pi }{4}}\sqrt{1+{\mathrm{tan}x}^{2}}dx={\int }_{\frac{\pi }{6}}^{\frac{\pi }{4}}\sqrt{{\mathrm{sec}}^{2}x}dx={\int }_{\frac{\pi }{6}}^{\frac{\pi }{4}}\mathrm{sec}xdx
Integramos indefinidamente.
{\int }_{\frac{\pi }{6}}^{\frac{\pi }{4}}\mathrm{sec}xdx=\left.\begin{array}{c}\\ \mathrm{ln}\left|\mathrm{sec}x+\mathrm{tan}x\right|\\ \end{array}\right]\begin{array}{c}\frac{\pi }{4}\\ \\ \frac{\pi }{6}\end{array}=\mathrm{ln}\left(1+\sqrt{2}\right)-\frac{1}{2}\mathrm{ln}\left(3\right)=\mathrm{ln}\left(1+\sqrt{2}\right)-\mathrm{ln}\left(\sqrt{3}\right)
\mathrm{ln}\left(1+\sqrt{2}\right)-\mathrm{ln}\left(\sqrt{3}\right)=\mathrm{ln}\left(\frac{1+\sqrt{2}}{\sqrt{3}}\right)
Finalmente:
L={\int }_{\frac{\pi }{6}}^{\frac{\pi }{4}}\sqrt{1+{\mathrm{tan}x}^{2}}dx=\mathrm{ln}\left(\frac{1+\sqrt{2}}{\sqrt{3}}\right)
La respuesta correcta es el inciso a).
Reactivo 49
Hallar el área encerrada entre las curvas f\left(x\right)={x}^{2} , g\left(x\right)=\frac{1}{x} y el eje x en el intervalo x\left[\frac{1}{2}, 2\right] . Tenga en cuenta que la intersección entre las curvas ocurre en P\left(1, 1\right) .
- I=0.985
- I=0.85
- I=1
Solución:
Iniciamos graficando las funciones para identificar los intervalos de integración para cada una.
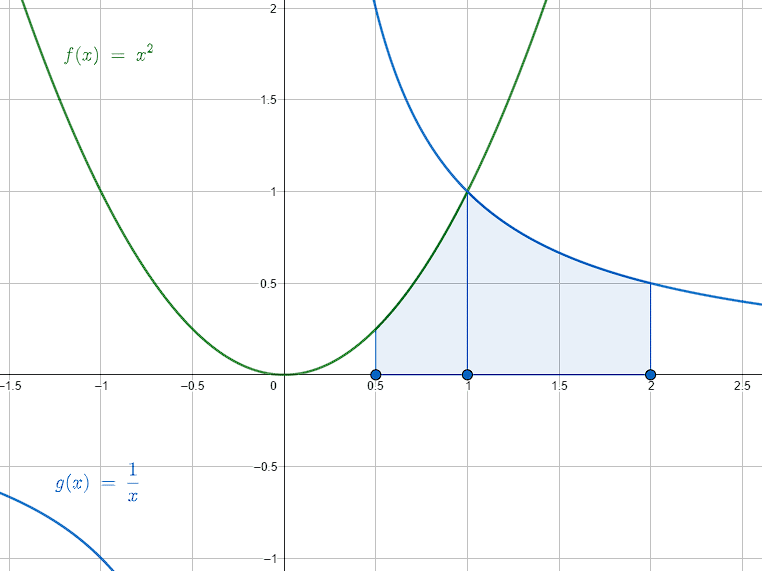
A={\int }_{\frac{1}{2}}^{1}{x}^{2}dx+{\int }_{1}^{2}\frac{1}{x}dx
Integramos indefinidamente.
A=\left.\frac{{x}^{3}}{3}\right]\begin{array}{c}1\\ \\ \frac{1}{2}\end{array}+\left.\begin{array}{c}\\ \mathrm{ln}\left|x\right|\\ \end{array}\right]\begin{array}{c}2\\ \\ 1\end{array}=\frac{1}{3}-\frac{1}{24}+\mathrm{ln}2-\mathrm{ln}1=\frac{7}{24}+\mathrm{ln}2
A=\frac{7}{24}+\mathrm{ln}2\approx 0.9848
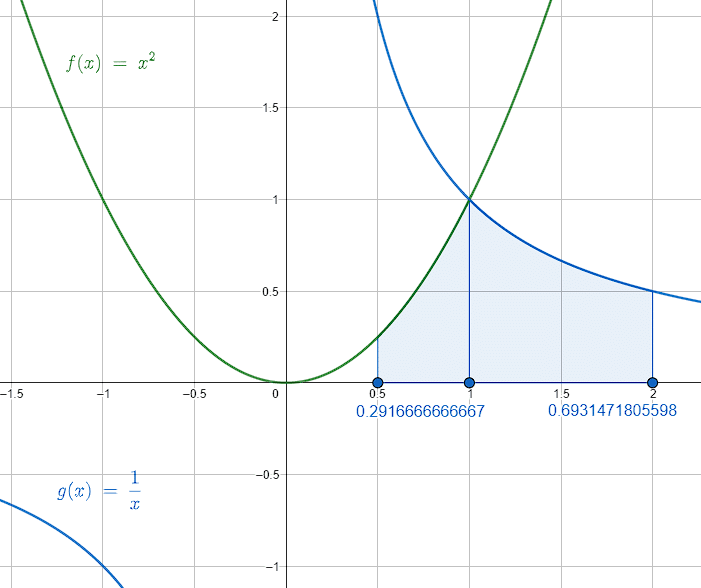
Comparando con los incisos, indicamos como respuesta correcta el a).
Reactivo 50
La catenaria, es una curva muy utilizada en arquitectura debido a que representa la mejor solución para la construcción de arcos, cuya ecuación viene descrita como:
y=a\mathrm{cosh}\left(\frac{x}{a}\right)
Ahora, el arco para determinada construcción, viene dado por la ecuación y=10-\mathrm{cosh}\left(x\right) y cuya gráfica es:

Calcule la longitud de dicho arco en el intervalo x\left[-3, 3\right] . Tenga en cuenta que:
\mathrm{sinh}x=\frac{{e}^{x}-{e}^{-x}}{2}; \mathrm{cosh}x=\frac{{e}^{x}+{e}^{-x}}{2}
{\mathrm{cosh}}^{2}x-{\mathrm{senh}}^{2}x=1
\int \mathrm{cosh}xdx=\mathrm{sinh}x+C
- L=\frac{1}{{e}^{3}}
- L=\frac{{e}^{6}-1}{{e}^{3}}
- L=\frac{-1}{{e}^{6}}
Solución:
Dejando a un lado el enunciado, que en su mayoría nos da contexto de la aplicación de la catenaria, debemos emplear la ecuación integral para calcular la longitud de una curva.
L={\int }_{a}^{b}\sqrt{1+{\left[{f}^{\text{'}}\left(x\right)\right]}^{2}}dx
Encontramos la derivada de la función.
{f}^{\text{'}}\left(x\right)={\left[10-\mathrm{cosh}\left(x\right)\right]}^{\text{'}}=-{\left[\mathrm{cosh}\left(x\right)\right]}^{\text{'}}
Vamos a sustituir al coseno hiperbólico por su expresión en términos de exponenciales.
{f}^{\text{'}}\left(x\right)=-{\left[\frac{{e}^{x}+{e}^{-x}}{2}\right]}^{\text{'}}=-\frac{1}{2}{\left({e}^{x}+{e}^{-x}\right)}^{\text{'}}=-\frac{1}{2}\left({e}^{x}-{e}^{-x}\right)=-\frac{{e}^{x}-{e}^{-x}}{2}
Esto es igual al seno hiperbólico.
{f}^{\text{'}}\left(x\right)=-\frac{{e}^{x}-{e}^{-x}}{2}=-\mathrm{sinh}x
Sustituimos a los extremos y a la función en la integral.
L={\int }_{-3}^{3}\sqrt{1+{\left[-\mathrm{sinh}x\right]}^{2}}dx={\int }_{-3}^{3}\sqrt{1+{\mathrm{sinh}}^{2}x}dx
Ahora, aplicamos la identidad del enunciado.
{\mathrm{cosh}}^{2}x-{\mathrm{senh}}^{2}x=1\to {\mathrm{cosh}}^{2}x=1+{\mathrm{senh}}^{2}x
Sustituimos.
{\int }_{-3}^{3}\sqrt{{\mathrm{cosh}}^{2}x}dx={\int }_{-3}^{3}{\mathrm{cosh}}^{2}xdx=\left.\begin{array}{c}\\ \mathrm{sinh}x\\ \end{array}\right]\begin{array}{c}3\\ \\ -3\end{array}
Evaluamos a la primitiva en los extremos de integración.
L=\left.\begin{array}{c}\\ \mathrm{sinh}x\\ \end{array}\right]\begin{array}{c}3\\ \\ -3\end{array}=\mathrm{sinh}3-\mathrm{sinh}-3=\frac{{e}^{3}-{e}^{-3}}{2}-\frac{{e}^{-3}-{e}^{3}}{2}=\frac{{e}^{3}}{2}-\frac{{e}^{-3}}{2}-\frac{{e}^{-3}}{2}+\frac{{e}^{3}}{2}
L={e}^{3}-\frac{1}{{e}^{3}}=\frac{{e}^{6}-1}{{e}^{3}}
La longitud de la curva es igual a \frac{{e}^{6}-1}{{e}^{3}} unidades.
La respuesta correcta es el inciso b).

