Examen Simulador IPN de Álgebra: Reactivos del 21 al 30

Continuando con la solución del examen simulacro de álgebra del IPN vamos a resolver los reactivos del 21 al 30.

Estos ejercicios te van a servir para repasar, reforzar y practicar la parte de matemáticas en el examen de admisión.

Reactivo 21

Representar con exponente fraccionario la siguiente expresión: \sqrt[3]{\left(3 x^{2}\right)^{4}}

1. (3 x)^{\frac{8}{3}}
2. 3^{\frac{2}{3}} x^{\frac{4}{3}}
3. \left(3 x^{2}\right)^{\frac{4}{3}}
4. (3 x)^{\frac{3}{4}}

Solución:

Para simplificar este monomio en forma de exponente racional, solo basta con aplicar la propiedad para exponentes racionales.

En este caso, 3 x^{2} se encuentra todo elevado a 4, quien sería el numerador de la fracción del exponente, además también está dentro de un radical de índice 3, quien pasaría a ser el denominador de la fracción.

Por lo tanto:

\sqrt[3]{\left(3 x^{2}\right)^{4}}=\left(3 x^{2}\right)^{\frac{4}{3}}

La respuesta correcta es la c).

Reactivo 22

Racionalizar la siguiente expresión fraccionaria: \frac{3}{\sqrt{x}+\sqrt{3}}

1. 3 \sqrt{x}+\sqrt{3}
2. 3 \sqrt{x}-\sqrt{3}
3. \frac{3(\sqrt{x}+\sqrt{3})}{x+3}
4. \frac{3(\sqrt{x}-\sqrt{3})}{x-3}

Solución:

Si examinamos los índices de los radicales, nos daremos cuenta de que ambos términos del denominador poseen raíces cuadradas, podemos multiplicar y dividir por el conjugado del denominador para que se asemeje al caso:

q-p=(\sqrt{q}-\sqrt{p})(\sqrt{q}+\sqrt{p})

Debemos multiplicar y dividir la fracción por \sqrt{x}-\sqrt{3} para deshacernos de los radicales.

\frac{3}{\sqrt{x}+\sqrt{3}} \frac{\sqrt{x}-\sqrt{3}}{\sqrt{x}-\sqrt{3}}=\frac{3(\sqrt{x}-\sqrt{3})}{(\sqrt{x}+\sqrt{3})(\sqrt{x}-\sqrt{3})}

\frac{3(\sqrt{x}-\sqrt{3})}{(\sqrt{x})^{2}-(\sqrt{3})^{2}}=\frac{3(\sqrt{x}-\sqrt{3})}{x-3}

Otra manera de ver lo que hemos hecho, es a partir del producto de los conjugados. Si desarrollamos el producto (a-b)(a+b) sabremos que tiene como resultado a^{2}-b^{2} .

Conclusión: la respuesta correcta es la d).

Reactivo 23

Simplificar la expresión: \frac{9 x^{6}}{3 x^{4}}

1. \frac{3}{9} x^{2}
2. \frac{9}{3} x^{10}
3. 3 x^{2}
4. 27 x^{24}

Solución:

Para simplificar esta última expresión, solo es necesario aplicar las reglas sobre exponentes que ya conocemos.

\frac{9 x^{6}}{3 x^{4}}=\frac{9}{3} \frac{x^{6}}{x^{4}}=3 x^{6-4}=3 x^{2}

Según las opciones propuestas por el problema, la correcta sería la c).

Reactivo 24

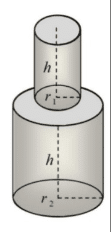
Indicar la fórmula del volumen de dos cilindros que tienen la misma altura, \sqrt{b^{3}}+\sqrt[3]{b^{2}} . Además, el radio del cilindro mayor es el triple del radio menor, \sqrt[5]{b^{3}} .

1. 10 \pi\left(b^{\frac{27}{10}}+a^{\frac{23}{15}}\right)
2. 10 \pi\left(b^{\frac{27}{10}}-b^{\frac{23}{15}}\right)
3. \pi\left(b^{\frac{27}{10}}+b^{\frac{23}{15}}\right)
4. 10 \pi\left(b^{\frac{27}{10}}+b^{\frac{28}{15}}\right)

Solución:

Para modelar matemáticamente lo que el problema está solicitando, es necesario conocer la ecuación para calcular el volumen de un cilindro.

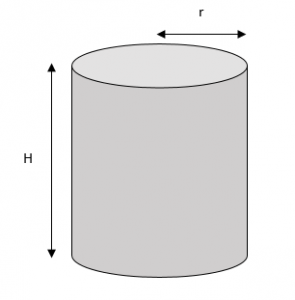
¿Qué es un cilindro?

Un cilindro es un cuerpo geométrico en tres dimensiones cuya forma se genera por el desplazamiento de un círculo a lo largo de una línea directriz (ortogonal u oblicua) de longitud finita h .

Existen diferentes tipos de cilindros, cuyas características diferenciadoras son: la inclinación de la línea directriz y la forma de la base, que puede ser circular, elíptica o cualquier otra figura plana. Al cilindro cuya directriz es ortogonal a la horizontal y de base circular se denomina cilindro rectangular circular y es el tipo que se presenta en el problema.

Existen diferentes alternativas para dar con la ecuación para calcular el volumen de un cilindro, pero la más sencilla es partir del área que tiene la base (esto es, solo válido en cilindros rectos).

Asumiremos cierto que el área de un círculo es A_{c i r}=\pi r^{2} , si a ese mismo círculo lo desplazamos a lo largo de la altura h estaríamos dando origen al cilindro en cuestión, por tanto la ecuación del volumen del cilindro recto de base circular queda como:

V_{c i l}=\pi r^{2} h

Retomando al problema, lo solicitado es el volumen de los dos cilindros juntos, es decir el volumen del cilindro menor de radio r_{1} sumado al volumen del cilindro mayor r_{2} , relación que se puede expresar:

V_{T}=V_{1}+V_{2}

V_{T}=\pi r_{1}^{2} h_{1}+\pi r_{2}^{2} h_{2}

Además, el problema nos dice que ambos poseen la misma altura y que el radio del mayor es tres veces el radio del menor.

h_{1}=h_{2}=h

r_{2}=3 r_{1}

Sustituyendo queda que:

V_{T}=\pi r_{1}^{2} h+\pi\left(3 r_{1}\right)^{2} h=\pi r_{1}^{2} h+\pi 9 r_{1}^{2} h=10 \pi r_{1}^{2} h

V_{T}=10 \pi r_{1}^{2} h

El problema también indica que:

r_{1}=\sqrt[5]{b^{3}}

h=\sqrt{b^{3}}+\sqrt[3]{b^{2}}

Sustituyendo nuevamente nos queda que:

V_{T}=10 \pi\left(\sqrt[5]{b^{3}}\right)^{2}\left(\sqrt{b^{3}}+\sqrt[3]{b^{2}}\right)

Aplicamos ahora el álgebra necesaria para simplificar la expresión:

V_{T}=10 \pi\left(\sqrt[5]{b^{6}} \sqrt{b^{3}}+\sqrt[5]{b^{6}} \sqrt[3]{b^{2}}\right)

V_{T}=10 \pi\left(b^{\frac{6}{5}} b^{\frac{3}{2}}+b^{\frac{6}{5}} b^{\frac{2}{3}}\right)

V_{T}=10 \pi\left(b^{\frac{6}{5}+\frac{3}{2}}+b^{\frac{6}{5}+\frac{2}{3}}\right)

V_{T}=10 \pi\left(b^{\frac{27}{10}}+b^{\frac{28}{15}}\right)

Concluimos que, según las opciones que ofrece el problema, la respuesta correcta es la d).

Reactivo 25

Identificar el desarrollo correspondiente a: (x-1)^{2}

1. x^{2}+x+1
2. x^{2}-x+1
3. x^{2}+2 x+1
4. x^{2}-2 x+1

Solución:

El desarrollo planteado es fácil de reconocer, ya que al realizar una rápida inspección de los productos notables demostrados con anterioridad, corresponde al cuadrado de la diferencia.

(a-b)^{2}=a^{2}-2 a b+b^{2}

Donde:

• a=x
• b=1

Sustituyendo se obtiene que:

(x-1)^{2}=(x)^{2}-2(x)(1)+(1)^{2}

(x-1)^{2}=x^{2}-2 x+1

Concluimos que la respuesta correcta es la d).

Reactivo 26

Relacionar ambas columnas de acuerdo con su respectivo producto notable.

Expresión	Resultado
1.       \left(2 x^{3}+3 x y^{2}\right)\left(2 x^{3}-3 x y^{2}\right)	A.      4 x^{6}-9 x^{2} y^{6}
2.       \left(2 x^{3}+3 y^{2}\right)\left(2 x^{3}-3 y^{2}\right)	B.      4 x^{6}-9 x^{2}
3.       \left(2 x^{3}+3 x\right)\left(2 x^{3}-3 x\right)	C.      4 x^{6}-9 y^{4}
4.       \left(2 x^{3}+3 x y^{3}\right)\left(2 x^{3}-3 x y^{3}\right)	D.      4 x^{6}-9 x^{2} y^{4}

1. 1D, 2C, 3B, 4A
2. 1D, 2C, 3A, 4B
3. 1B, 2D, 3A, 4C
4. 1B, 2D, 3C, 4A

Solución:

Para lograr relacionar los elementos de cada columna, es necesario desarrollar las expresiones en la columna de la izquierda. El producto notable que utilizaremos en este caso es:

El producto de la suma de dos números por su diferencia

(a+b)(a-b)=a^{2}-b^{2}

Aquí rescatamos lo dicho antes de que \text{a y b} no se limitan a solo variables únicas. a será lo que tengamos a la izquierda y b a la derecha. Esto también se realiza a conveniencia, según lo que necesites demostrar, simplificar o desarrollar.

1. \left(2 x^{3}+3 x y^{2}\right)\left(2 x^{3}-3 x y^{2}\right)

a=2 x^{3} \text{ y } b=3 x y^{2}

\left(2 x^{3}+3 x y^{2}\right)\left(2 x^{3}-3 x y^{2}\right)=\left(2 x^{3}\right)^{2}-\left(3 x y^{2}\right)^{2}

Aplicando propiedades de los exponentes:

\left(2 x^{3}+3 x y^{2}\right)\left(2 x^{3}-3 x y^{2}\right)=4 x^{6}-9 x^{2} y^{4}

4 x^{6}-9 x^{2} y^{4} \rightarrow D

2. \left(2 x^{3}+3 y^{2}\right)\left(2 x^{3}-3 y^{2}\right)

a=2 x^{3} \text{ y } b=3 y^{2}

\left(2 x^{3}+3 y^{2}\right)\left(2 x^{3}-3 y^{2}\right)=\left(2 x^{3}\right)^{2}-\left(3 y^{2}\right)^{2}

\left(2 x^{3}+3 y^{2}\right)\left(2 x^{3}-3 y^{2}\right)=4 x^{6}-9 y^{4}

4 x^{6}-9 y^{4} \rightarrow C

3. \left(2 x^{3}+3 x\right)\left(2 x^{3}-3 x\right)

a=2 x^{3} \text{ y } b=3 x

\left(2 x^{3}+3 x\right)\left(2 x^{3}-3 x\right)=\left(2 x^{3}\right)^{2}-(3 x)^{2}

\left(2 x^{3}+3 x\right)\left(2 x^{3}-3 x\right)=4 x^{6}-9 x^{2}

4 x^{6}-9 x^{2} \rightarrow B

4. \left(2 x^{3}+3 x y^{3}\right)\left(2 x^{3}-3 x y^{3}\right)

a=2 x^{3} \text{ y } b=3 x y^{3}

\left(2 x^{3}+3 x y^{3}\right)\left(2 x^{3}-3 x y^{3}\right)=\left(2 x^{3}\right)^{2}-\left(3 x y^{3}\right)^{2}

\left(2 x^{3}+3 x y^{3}\right)\left(2 x^{3}-3 x y^{3}\right)=4 x^{6}-9 x^{2} y^{6}

4 x^{6}-9 x^{2} y^{6} \rightarrow A

Según los resultados, se concluye que: 1D, 2C, 3B, 4A. Comparando con las opciones, la respuesta correcta es la a).

Reactivo 27

Completar el siguiente binomio al cuadrado: \left(a^{2}+\frac{b}{2}\right)^{2}=?+a^{2} b+\frac{b^{2}}{?}

1. -a^{4},-4
2. a^{4},-4
3. -a^{4},4
4. a^{4},4

Solución:

Encontrar respuesta a este problema es sencillo. Queda claro que el producto notable que hay que utilizar es:

El cuadrado de la suma de dos números

(x+y)^{2}=x^{2}+2 x y+y^{2}

Donde:

x=a^{2} y=\frac{b}{2}

Sustituyendo y aplicando la fórmula:

\left(a^{2}+\frac{b}{2}\right)^{2}=a^{4}+a^{2} b+\frac{b^{2}}{4}

La respuesta correcta sería la d) a^{4},4 .

Reactivo 28

¿Cuál es el resultado del producto notable (a+2-b)(a+2+b) ?

1. a^{2}-b^{2}-4 a-4
2. a^{2}+b^{2}-4 a-4
3. a^{2}-b^{2}+4 a+4
4. a^{2}+b^{2}+4 a+4

Solución:

Aunque parece que tendremos que desarrollar el producto paso a paso de los polinomios, es posible aplicar un truco astuto para simplificar mucho los cálculos. Vemos que a+2 se mantiene en ambas expresiones. El último término es la b con signo cambiado en ambos trinomios.

El producto notable que concuerda con la expresión es:

La suma de dos números por su diferencia

(x+y)(x-y)=x^{2}-y^{2}

x=\mathrm{a}+2, y=b

Agrupando nos queda que:

[(a+2)+b][(a+2)-b]=(a+2)^{2}-b^{2}

Desarrollamos al producto notable (a+2)^{2}

(a+2)^{2}-b^{2}=a^{2}+4 a+4-b^{2}

(a+2-b)(a+2+b)=a^{2}-b^{2}+4 a+4

Según las opciones que indica el problema, la correcta es c).

Reactivo 29

Dado el polinomio: -10 r^{3} s^{2} t^{4}+15 r^{2} s^{4} t^{3}-5 r^{2} s^{2} t^{3}

Identificar el factor común sin que se tengan fracciones.

1. 5 r^{2} s^{2} t^{2}
2. 5 r^{2} s^{2} t^{3}
3. 5 r^{3} s^{2} t^{4}
4. 5 r^{3} s^{4} t^{4}

Solución:

Para encontrar la factorización a este polinomio, solo hay que calcular el factor común entre sus términos.

El procedimiento es sencillo, solo hay que identificar las letras que se repitan en los tres términos con sus menores exponentes y determinar el máximo común divisor entre los coeficientes numéricos.

Letras presentes en todos los términos: r, s \text{ y } t . Por inspección, sabemos que sus mínimos exponentes son: 2, 2 y 3 respectivamente.

r^{2} s^{2} t^{3}

Máximo común divisor entre los coeficientes:

M C D(10,15,5)=5

El monomio factor común entre los términos es entonces:

5 r^{2} s^{2} t^{3}

La expresión factorizada quedaría como:

-10 r^{3} s^{2} t^{4}+15 r^{2} s^{4} t^{3}-5 r^{2} s^{2} t^{3}=5 r^{2} s^{2} t^{3}\left(-2 r t+3 s^{2}-1\right)

Conclusión, la respuesta correcta según las opciones dadas por el problema es la b).

Reactivo 30

Factorizar la siguiente expresión: 20 a m-5 b m-2 b n+8 a n

1. (-5 b m-2 b n)(20 a m+8 a n)
2. (20 a m-5 b m)(2 b n+8 a n)
3. (4 a+b)(5 m-2 n)
4. (4 a-b)(5 m+2 n)

Solución:

El método de factorización que aplicaremos en este caso es por agrupación de términos. Comenzaremos por agrupar los términos cuyos coeficientes tengan máximo común divisor distinto de cero y además, posean letras comunes.

20 a m-5 b m-2 b n+8 a n=20 a m-5 b m+8 a n-2 b n

20 a m-5 b m+8 a n-2 b n=(20 a m-5 b m)+(8 a n-2 b n)

Para el primer conjunto el MCD es 5 y la letra común es la m. En el segundo grupo el MCD es 2 y la letra común la n.

(20 a m-5 b m)+(8 a n-2 b n)=5 m(4 a-b)+2 n(4 a-b)

Ahora se extrae factor común al polinomio (4 a-b)

5 m(4 a-b)+2 n(4 a-b)=(4 a-b)(5 m+2 n)

Conclusión, la respuesta correcta según las opciones dadas por el problema es la d).