Seguimos con la segunda parte del examen simulacro de física del IPN para las carreras del área de Ingenierías y Ciencias Físico Matemáticas.

Recuerda intentar resolver los ejercicios por tu cuenta, antes de consultar la respuesta correcta, vamos a continuar con los reactivos del 11 al 20.
Reactivo 11
Un automóvil se desplaza por una carretera con una rapidez de 10 metros por segundo. En determinado momento, acelera a razón de 4 \mathrm{m}/{\mathrm{s}}^{2} durante 10 segundos. Calcule el desplazamiento total.
- 200 m
- 300 m
- 400 m
- 500 m
Solución:
Si analizamos el enunciado, nos daremos cuenta que describe un movimiento uniformemente acelerado el cual inicia con una rapidez de 10 \mathrm{m}/\mathrm{s} , que incrementa a razón de 4 \mathrm{m}/{\mathrm{s}}^{2} y dura 10 segundos.
Debido a que nos piden el desplazamiento total, podemos asumir que el MUA comienza desde el origen de coordenadas. La ecuación a emplear en este caso será:
{x}_{f}={x}_{o}+{v}_{o}t+\frac{a{t}^{2}}{2}
Sustituimos los datos.
{x}_{f}=0+\left(10\right)\left(10\right)+\frac{\left(4\right){\left(10\right)}^{2}}{2}=300 \mathrm{m}
El coche recorre 300 metros durante el MUA.
La respuesta correcta es el inciso b).
Reactivo 12
A partir del sistema que se muestra en la figura, calcule la distancia a la que debe colocar la masa respecto al punto O para que el sistema permanezca en equilibrio.
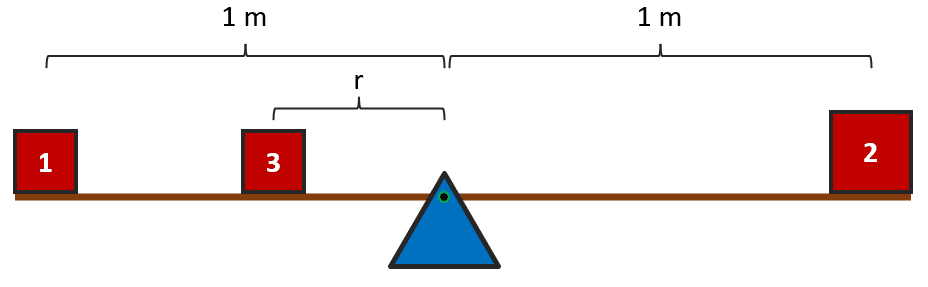
Considere: {m}_{1}=0.5 \mathrm{k}\mathrm{g} , {m}_{2}=2 \mathrm{k}\mathrm{g} y {m}_{3}=1 \mathrm{k}\mathrm{g} .
- 0.5 \mathrm{m}
- 1 \mathrm{m}
- 1.5 \mathrm{m}
- 2.5 \mathrm{m}
Solución:
Para resolver este problema, debemos aplicar la condición de estabilidad mecánica respecto a las torcas. Nuestro eje de rotación será el punto de pivote de la balanza y asumimos torcas positivas en sentido antihorario.
Estabilidad respecto a torcas.
\sum \tau =0
Las masas 1 y 3 producen torcas positivas y la masa 2 torca negativa.
{\tau }_{1}+{\tau }_{3}-{\tau }_{2}=0
Recordemos que las torcas se calculan como el producto de la fuerza por el radio. En nuestro caso, las fuerzas corresponden a los pesos de las masas.
{\tau }_{1}+{\tau }_{3}-{\tau }_{2}=0\to {r}_{1}{m}_{1}g+{r}_{3}{m}_{3}g-{r}_{2}{m}_{2}g=0
Podemos simplificar la gravedad en todos los términos. Despejamos a {r}_{3} , nuestra incógnita.
{r}_{3}{m}_{3}={r}_{2}{m}_{2}-{r}_{1}{m}_{1}\to {r}_{3}=\frac{{r}_{2}{m}_{2}-{r}_{1}{m}_{1}}{{m}_{3}}
{r}_{3}=\frac{\left(1\right)\left(2\right)-\left(1\right)\left(0.5\right)}{1}=1.5 \mathrm{m}
La masa 3 debe colocarse a 1.5 metros respecto al eje de giro para que el sistema sea estable.
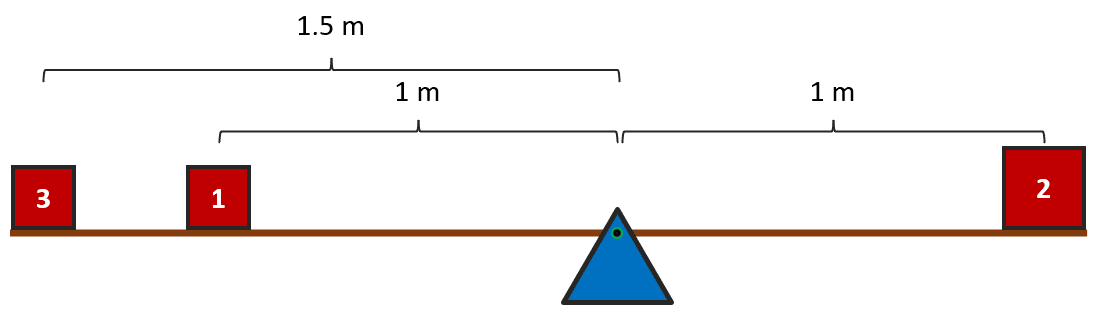
La respuesta correcta es el inciso c).
Reactivo 13
¿Cuál será la posición angular de una partícula que describe un MCU al transcurrir 5 segundos, si tiene una frecuencia de 4 Hz?
- 0°
- 22°
- 180°
- 90°
Solución:
En el movimiento circular uniforme, la velocidad angular se relaciona con la frecuencia a través de la siguiente expresión:
\omega =2\pi f
A su vez, la velocidad angular se puede expresar como:
\omega =\frac{\mathrm{\Delta }\theta }{\mathrm{\Delta }t}
Despejando el desplazamiento angular nos queda:
\mathrm{\Delta }\theta =\omega \cdot \mathrm{\Delta }t=2\pi f\mathrm{\Delta }t
Sustituimos f=4 \mathrm{H}\mathrm{z} y \mathrm{\Delta }t=5 \mathrm{s} .
\mathrm{\Delta }\theta =2\pi \left(4\right)\left(5\right)=40\pi
Transformando a grados.
\mathrm{\Delta }\theta =7200°
Llevándolo a una sola vuelta.
\mathrm{\Delta }\theta =0°
Pasados 5 segundos y con una frecuencia de 4 Hz, la partícula tiene una posición angular de 0°.
La respuesta correcta es el inciso a).
Reactivo 14
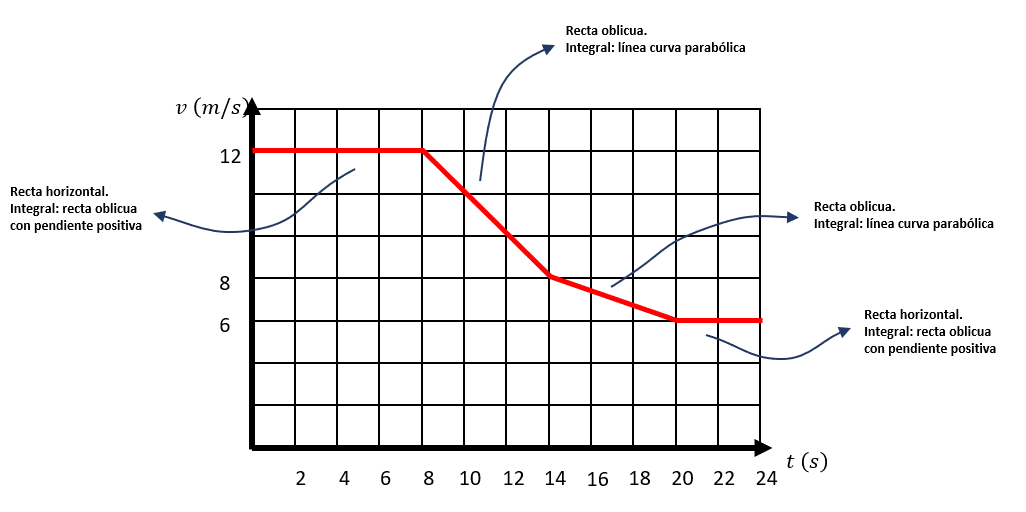
La siguiente gráfica corresponde a la rapidez en función del tiempo de un automóvil. Identifique el tipo de movimiento en cada tramo.
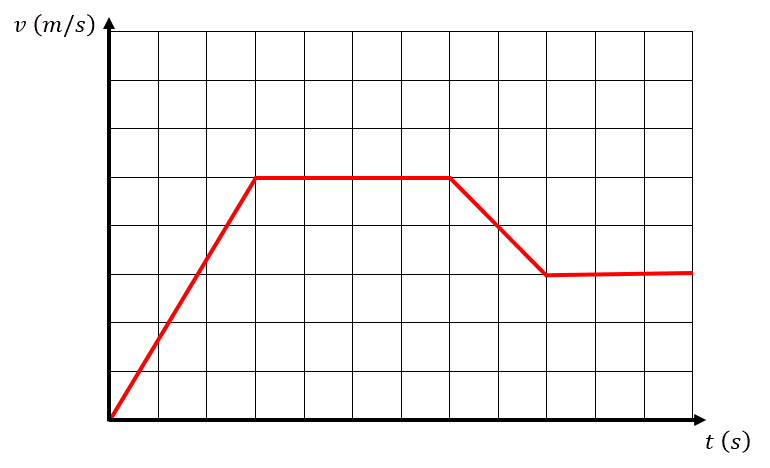
- MRU – MRU – MRUA – MRU
- MRUA – MRU – MRUA – MRU
- MRU – MRU – MRU – MRU
- MRU – MRUA – MRU – MRUA
Solución:
Recordemos que un movimiento rectilíneo uniforme es aquel donde la velocidad permanece constante, gráficamente esto se representa por una línea horizontal.
Por otro lado, el movimiento es rectilíneo y uniformemente acelerado, cuando la velocidad es una recta inclinada, puede ser de pendiente positiva (aceleración positiva) o negativa (movimiento desacelerado).
Teniendo esto en cuenta y examinando la gráfica, podemos decir que el primer tramo es un MRUA, el segundo un MRU, el tercero un MRUA y el cuarto MRU.
MRUA – MRU – MRUA – MRU.
Concluimos que la respuesta correcta es el inciso b).
Reactivo 15
Complete la siguiente frase correctamente.
Las fuerzas que actúan sobre un cuerpo se anulan cuando…
- Se mueve cercano a la luz
- Su aceleración es constante
- Su velocidad es nula o constante
- Su masa es despreciable
Solución:
A partir de la mecánica clásica y de las leyes de Newton, sabemos que la sumatoria de fuerzas sobre un cuerpo es igual al producto de su masa por la aceleración.
\sum F=ma
Esto puede escribirse en términos de la velocidad como:
\sum F=m\frac{dv}{dt}
Ahora, igualando esta sumatoria de fuerzas a cero nos queda:
\sum F=0\to m\frac{dv}{dt}=0
Dicha igualdad se cumple cuando la masa es cero o la derivada de la velocidad respecto al tiempo es cero. La masa del cuerpo no puede ser nula, por tanto, lo descartamos. Nos queda la derivada de la velocidad, una derivada se anula cuando la función es una constante o directamente cero.
\frac{dv}{dt}=0\to v=\mathrm{c}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{ }\mathrm{o}\mathrm{ }v=0
En conclusión: para que las fuerzas aplicadas sobre un cuerpo se anulen, el mismo tiene que estar en reposo o moverse con velocidad constante. Comparando con los incisos, la respuesta correcta es c).
Reactivo 16
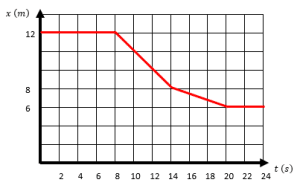
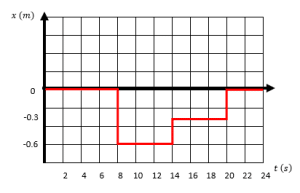
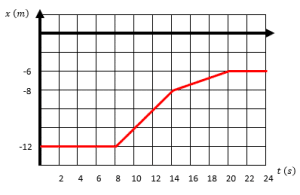
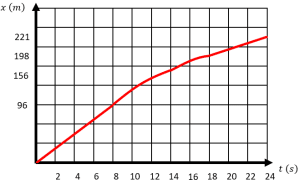
A partir de la gráfica de rapidez en función del tiempo de un móvil, obtenga la gráfica de desplazamiento en función del tiempo.
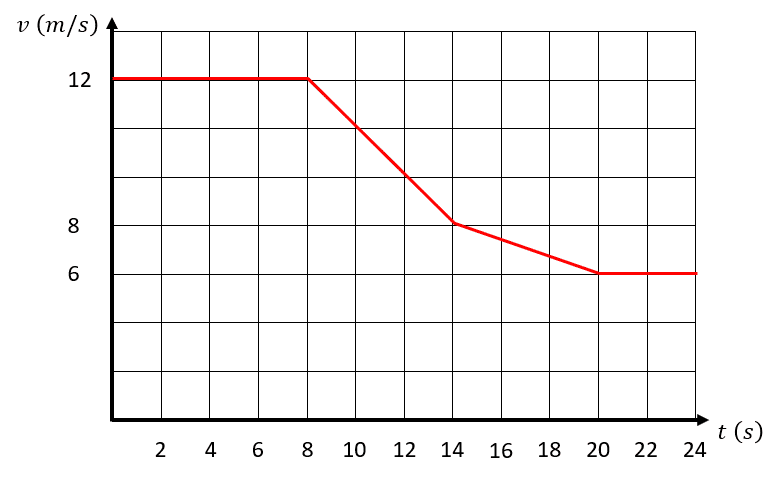
Solución:
En este caso, debemos tener en cuenta la relación que existe entre la rapidez y el desplazamiento de un cuerpo.
x\left(t\right)=\int v\left(t\right)dt
El desplazamiento es igual a la integral de la rapidez.
Ahora, podríamos tomar dos enfoques para resolver este problema. El primero consiste en calcular las funciones de rapidez para cada intervalo, luego integrarlas y finalmente graficarlas. Esto es más preciso, pero no es útil durante el examen, porque tardarías mucho tiempo.
El otro enfoque consiste en identificar el tipo de función que se obtiene al integrar la rapidez, con pura inspección visual. Recordemos que al integrar líneas horizontales obtenemos rectas inclinadas y al integrar rectas inclinadas obtenemos curvas parabólicas.
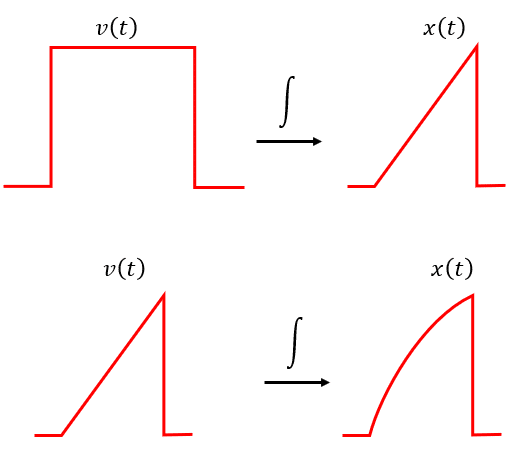
Con esta simplificación, podemos ir a la gráfica del enunciado y establecer la función que esperamos al integrar.
Examinando los incisos nos damos cuenta que las tres primeras opciones son gráficas con líneas rectas, no hay ninguna curva. Por otro lado, el inciso d cumple con las características antes mencionadas.
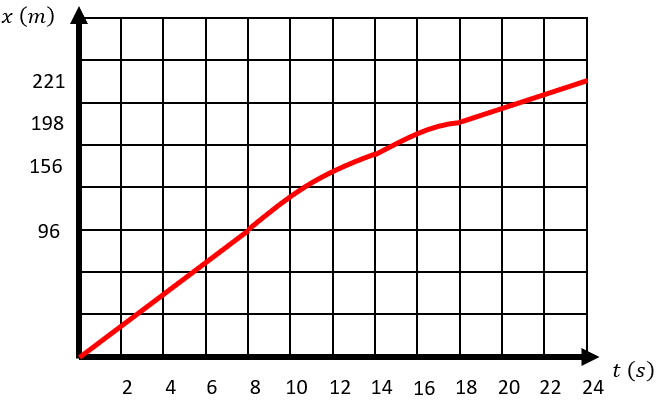
Concluimos que la respuesta correcta es el inciso d).
Reactivo 17
Durante un juego de béisbol, un bateador conecta la bola de tal forma que los equipos del estadio registran una altura máxima de 150 metros y un recorrido horizontal de 280 metros. Si la altura desde la que sale disparada se considera despreciable y la aceleración de la gravedad es de 10 \mathrm{m}/{\mathrm{s}}^{2} , calcule el módulo de la rapidez inicial.
- 40.44\frac{\mathrm{m}}{\mathrm{s}}
- 50.44\frac{\mathrm{m}}{\mathrm{s}}
- 60.44\frac{\mathrm{m}}{\mathrm{s}}
- 70.44\frac{\mathrm{m}}{\mathrm{s}}
Solución:
Debido a que se trata de una bola que es bateada, el tipo de movimiento que experimenta es de tiro parabólico. Las ecuaciones de cinemática para este movimiento son:
\mathrm{h}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{z}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{l}:{x}_{f}={x}_{o}+{v}_{x}t
\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}:\mathrm{ }\left\{\begin{array}{c}{y}_{f}={y}_{o}+{v}_{oy}t-\frac{g{t}^{2}}{2}\\ {v}_{fy}={v}_{o}+ta\\ {v}_{fy}^{2}={v}_{oy}^{2}-2g\Delta y\end{array}\right.
Además, sabemos que el módulo de la velocidad inicial se calcula como:
{v}_{o}=\sqrt{{v}_{x}^{2}+{v}_{oy}^{2}}
En este caso, vamos a calcular por separado las componentes de la velocidad inicial para luego aplicar la ecuación anterior. Comencemos con el movimiento vertical.
El enunciado nos dice la altura máxima que alcanza la bola, en este instante la velocidad {v}_{fy} se anula, por tanto, podríamos despejar la rapidez inicial en y con la tercera ecuación.
{v}_{fy}^{2}={v}_{oy}^{2}-2g\mathrm{\Delta }y\to 0={v}_{oy}^{2}-2g\mathrm{\Delta }y
{v}_{oy}=\sqrt{2g\mathrm{\Delta }y}
Sustituimos.
{v}_{oy}=\sqrt{2\left(10\right)\left(150\right)}=54.77 \mathrm{m}/\mathrm{s}
Para calcular la rapidez horizontal, necesitamos el tiempo de vuelo de la bola, este se obtiene con la siguiente ecuación:
{t}_{v}=\frac{2{v}_{oy}}{g}
Sustituimos.
{t}_{v}=\frac{2\left(54.77\right)}{10}=10.95 \mathrm{s}
Con el desplazamiento horizontal total y el tiempo de vuelo, despejamos la rapidez horizontal.
{v}_{x}=\frac{{x}_{f}-{x}_{o}}{{t}_{v}}=\frac{280 \mathrm{m}}{10.95 \mathrm{s}}=25.57 \mathrm{m}/\mathrm{s}
Finalmente, calculamos el módulo de la velocidad inicial.
{v}_{o}=\sqrt{{54.77}^{2}+{25.57}^{2}}=60.44 \mathrm{m}/\mathrm{s}
La bola salió disparada con una rapidez inicial de 60.44 metros por segundo.
La respuesta correcta es el inciso c).
Reactivo 18
Para medir de forma indirecta la altura de un edificio de muchos pisos, un grupo de estudiantes ha decidido dejar caer una pelota desde la azotea y medir el tiempo que tarda en llegar al suelo. Luego de varios intentos, obtuvieron que el tiempo promedio de caída es de 15 segundos. Si la aceleración de la gravedad es de 10 \mathrm{m}/{\mathrm{s}}^{2} , calcule la altura del edificio.
- -1125 \mathrm{m}
- 11250 \mathrm{m}
- 1250 \mathrm{m}
- 1125 \mathrm{m}
Solución:
Comenzamos planteando la ecuación de altura en función del tiempo para cuerpos en caída libre.
{y}_{f}={y}_{o}+{v}_{o}t-\frac{g{t}^{2}}{2}
Debido a que la pelota se deja caer, la velocidad inicial es cero. Por otro lado, suponemos que el origen de coordenadas es la azotea del edificio, por tanto, {y}_{o}=0 \mathrm{m} .
{y}_{f}=-\frac{g{t}^{2}}{2}
Sustituimos los valores de gravedad y tiempo.
{y}_{f}=-\frac{\left(10\right){\left(15\right)}^{2}}{2}=-1125 \mathrm{m}
Ignoramos el signo negativo, ya que esto se debe al punto en el que hemos colocado nuestro sistema de referencia. Si éste hubiera sido el suelo, el valor sería positivo. Concluimos entonces que el edificio mide 1125 metros y que la respuesta correcta es el inciso d).
Reactivo 19
A partir del sistema que se muestra en la figura, calcule el ángulo \alpha para que permanezca en equilibrio.
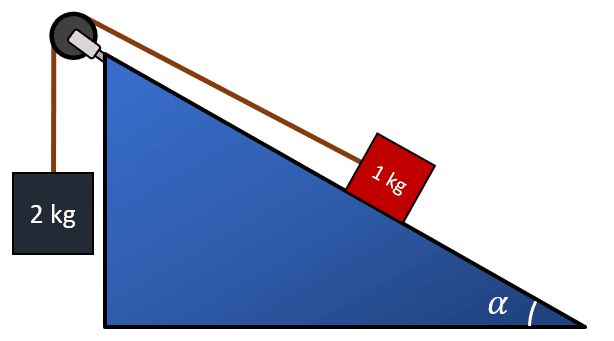
Considere despreciable la fricción entre el plano y la masa de 1 kg.
- 33°
- No existe
- 45°
- 60°
Solución:
Para calcular el valor de \alpha , debemos aplicar la primera Ley de Newton en los dos bloques del sistema. Comencemos por dibujar el DCL del bloque de 1 kg.
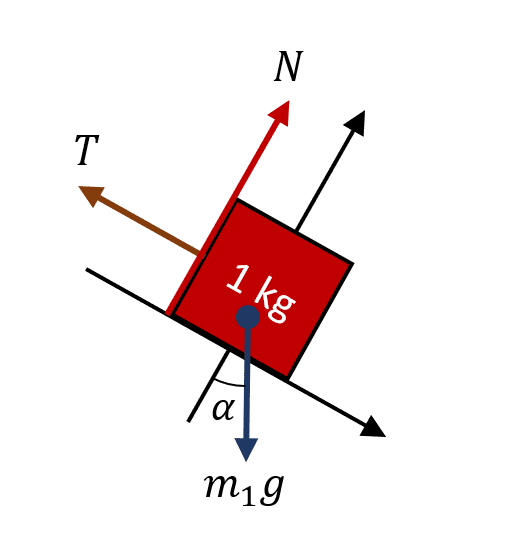
Debido a que el bloque solo podría desplazarse en la dirección de la tensión de la cuerda, podemos ignorar sin cuidado el análisis sobre el eje y del sistema. Aplicando la condición de equilibrio obtenemos:
\sum {F}_{x}=0\to {m}_{1}g\mathrm{sin}\alpha -T=0
Despejando la tensión:
T={m}_{1}g\mathrm{sin}\alpha
Ahora, dibujamos el DCL para la masa de 2 kg.
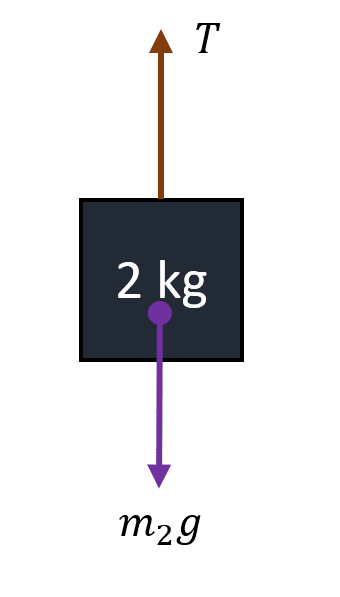
Aplicando la primera Ley de Newton nos queda:
\sum {F}_{y}=0\to T-{m}_{2}g=0
Despejamos la tensión de la cuerda.
T={m}_{2}g
Igualamos ambas ecuaciones.
{m}_{2}g={m}_{1}g\mathrm{sin}\alpha \to \mathrm{sin}\alpha =\frac{{m}_{2}}{{m}_{1}}
Sustituimos el valor de las masas.
\mathrm{sin}\alpha =\frac{{m}_{2}}{{m}_{1}}=\frac{2}{1}=2
Como sabemos, el seno es una función acotada entre -1 y 1, por tanto, no existe ningún ángulo que podamos sustituir que dé como resultado 2. La conclusión de esto es que: no hay ángulo que haga al sistema estático.
Si analizamos un poco la situación, estamos encargándole a una masa pequeña que sostenga a una masa más grande, ni con un ángulo de 90° (seno en su valor máximo) podríamos mantener el sistema en equilibrio.
La respuesta correcta es la opción b).
Reactivo 20
¿Cuál debería ser la relación entre las masas de dos cuerpos que se encuentran conectados a través de una cuerda y cuelgan verticalmente mediante una polea, para que el sistema permanezca en equilibrio?
- {m}_{1}={m}_{2}
- {m}_{1}=\frac{{m}_{2}}{2}
- {m}_{1}=3{m}_{2}
- {m}_{1}=2{m}_{2}
Solución:
Antes de aplicar las ecuaciones de Newton, hagamos un dibujo de la situación planteada por el enunciado.
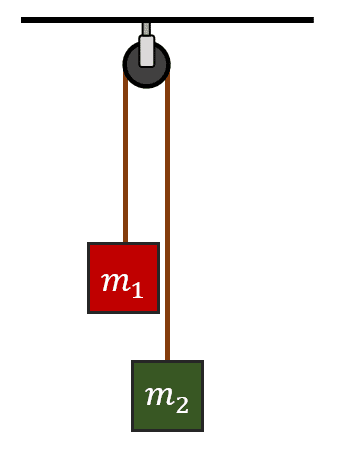
Si hiciéramos el DCL para ambas masas, encontraríamos que cada una experimenta una fuerza de tensión que las tira hacia arriba, mientras que su propio peso tira de ellas hacia abajo. En ecuaciones, esto quedaría:
T-{m}_{1}g=0 y T-{m}_{2}g=0
Aplicamos la primera ley de Newton porque el enunciado nos pide estabilidad. Despejando la tensión en ambas ecuaciones e igualando las expresiones nos queda:
T={m}_{1}g, T={m}_{2}g\to {m}_{1}g={m}_{2}g
Simplificando.
{m}_{1}={m}_{2}
Las masas deben ser iguales para que el sistema sea estable.
Concluimos que la respuesta correcta es la a).