¡Seguimos aspirante! En este tutorial vamos a resolver la cuarta parte del simulacro de matemáticas para el examen de ingreso al IPN por el área de Ingeniería y Ciencias Físico-Matemáticas, desde el 31 al 40.

Resuélvelos por tu cuenta antes de revisar la solución. Además, estudia los fundamentos y recuerda que lo más importante es tu capacidad para la solución de problemas.
Ejercicios de Matemáticas
Continuamos con los siguientes 10 reactivos del simulacro de matemáticas, de cara a la prueba de ingreso del Instituto Politécnico Nacional.
Reactivo 31
Calcule el valor de la integral {\int }_{-1}^{5}\sqrt{x+1}dx .
- \sqrt{6}
- 2\sqrt{6}
- 3\sqrt{6}
- 4\sqrt{6}
Solución:
Para calcular el valor de cualquier integral definida, primero debemos calcular la primitiva de la función integrando y luego aplicar el teorema fundamental del cálculo.
{\int }_{a}^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right)
Donde F es la primitiva de f .
Examinando la integral, nos damos cuenta que el diferencial de x+1 es dx , por tanto, en este caso solo debemos aplicar la fórmula de integración de una potencia.
{\int }_{-1}^{5}\sqrt{x+1}dx={\int }_{-1}^{5}{\left(x+1\right)}^{1/2}dx=\left.\frac{{2\left(x+1\right)}^{\frac{3}{2}}}{3}\right]\begin{array}{c}5\\ \\ -1\end{array}
Aplicamos el teorema fundamental del cálculo.
=\frac{{2\left(5+1\right)}^{\frac{3}{2}}}{3}-\frac{{2\left(-1+1\right)}^{\frac{3}{2}}}{3}=4\sqrt{6}
Finalmente:
{\int }_{-1}^{5}\sqrt{x+1}dx=4\sqrt{6}
Comparando con los incisos, concluimos que la respuesta correcta es la d).
Reactivo 32
Determine el valor de la siguiente integral definida.
{\int }_{0}^{\frac{\pi }{2}}\mathrm{sin}\theta d\theta
- -1
- 0
- 1
- \pi
Solución:
Iniciamos por calcular la primitiva del seno que, según las fórmulas de integración es \mathrm{cos}\theta .
{\int }_{0}^{\frac{\pi }{2}}\mathrm{sin}\theta d\theta =\left.-\mathrm{cos}\theta \right]\begin{array}{c}\frac{\pi }{2}\\ 0\end{array}
Aplicando el teorema fundamental del cálculo:
=-\mathrm{cos}\frac{\pi }{2}+\mathrm{cos}0=1
Finalmente:
{\int }_{0}^{\frac{\pi }{2}}\mathrm{sin}\theta d\theta =1
Comparando con las opciones, seleccionamos como correcta la c).
Reactivo 33
Identifique la identidad trigonométrica que simplifica la siguiente integral.
\int {\mathrm{sin}}^{2}xdx
- \frac{1-\mathrm{cos}2x}{2}
- 1-{\mathrm{cos}}^{2}x
- \frac{1+\mathrm{cos}2x}{2}
- \mathrm{csc}x
Solución:
Cuando tratamos con identidades trigonométricas, debemos tener presente que buscamos una expresión simplificada que, en este caso, nos permite calcular la integral. El seno al cuadrado no se encuentra en las tablas y la identidad pitagórica tampoco nos ayudará a simplificar el problema.
\int {\mathrm{sin}}^{2}xdx=\int \left(1-{\mathrm{cos}}^{2}x\right)dx
Continuamos teniendo una identidad al cuadrado, no funciona. La única identidad que nos podría ayudar es:
{\mathrm{sin}}^{2}x=\frac{1-\mathrm{cos}2x}{2}
Esta no tiene ninguna otra identidad al cuadrado y puede integrarse aplicando de forma casi directa la fórmula integral del coseno. Concluimos entonces que esta es la identidad que simplifica la integral.
\int {\mathrm{sin}}^{2}xdx=\frac{1}{2}\int \left(1-\mathrm{cos}2x\right)dx
El inciso con la respuesta correcta es el a).
Reactivo 34
Identifique cuál de las siguientes opciones es la antiderivada de la función y=\frac{6{x}^{2}-11x+7}{3x-1}
- {x}^{2}-3x+\frac{4}{3}\mathrm{ln}\left|3x-1\right|+C
- {x}^{2}-3x+\frac{4}{3}\mathrm{ln}\left|x-1\right|+C
- {x}^{2}+3x+\frac{4}{3}\mathrm{ln}\left|3x-1\right|+C
- \frac{{x}^{2}}{2}-3x+\frac{4}{3}\mathrm{ln}\left|3x-1\right|+C
Solución:
En las integrales donde se presenta un cociente de funciones polinómicas, podemos intentar 3 cosas: separar en fracciones parciales, división de polinomios o eliminación de factores comunes. En este caso, el numerador no posee raíces reales, por tanto, queda descartada la tercera opción.
Aplicamos división de polinomios, ya que el grado del numerador es mayor al denominador.

El primer término del cociente será 2x para eliminar al 6{x}^{2} .
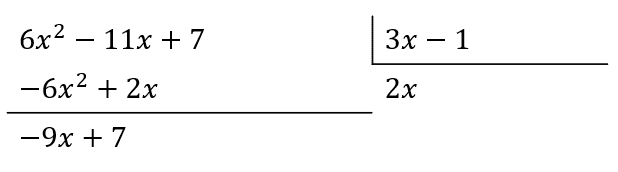
Para eliminar al -9x el siguiente término del cociente es -3 .
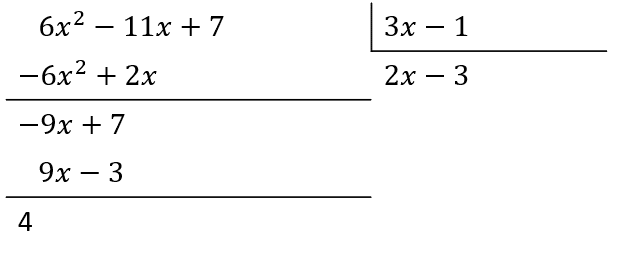
Reescribimos la integral:
\int \left(2x-3+\frac{4}{3x-1}\right)dx
Separamos en términos:
=2\int xdx-3\int dx+4\int \frac{dx}{3x-1}
Aplicando la fórmula integral de una potencia, la de una constante y la del inverso de x , respectivamente, nos queda:
={x}^{2}-3x+\frac{4}{3}\mathrm{ln}\left|3x-1\right|+C
Finalmente:
\int \frac{6{x}^{2}-11x+7}{3x-1}dx={x}^{2}-3x+\frac{4}{3}\mathrm{ln}\left|3x-1\right|+C
Comparando con los incisos, concluimos que la respuesta correcta se encuentra en a).
Reactivo 35
Calcular el resultado de la siguiente integral.
\int \frac{1}{1-3a}da
- -\frac{1}{3}\mathrm{ln}\left|a+\frac{1}{3}\right|+C
- \mathrm{ln}\left|a-\frac{1}{3}\right|+C
- -\frac{1}{3}\mathrm{ln}\left|a-\frac{1}{3}\right|+C
- \frac{1}{3}\mathrm{ln}\left|a-\frac{1}{3}\right|+C
Solución:
En este caso, debemos acomodar un poco la expresión del denominador del integrando para aplicar la fórmula integral:
\int \frac{1}{u}du=\mathrm{ln}\left|u\right|+C
Comenzamos extrayendo factor común el -3.
\int \frac{1}{1-3a}da=\int \frac{1}{-3\left(-\frac{1}{3}+a\right)}da=-\frac{1}{3}\int \frac{1}{\left(a-\frac{1}{3}\right)}da
En este caso, el diferencial de a-\frac{1}{3} es da por tanto, ya podemos aplicar la fórmula integral.
-\frac{1}{3}\int \frac{1}{\left(a-\frac{1}{3}\right)}da=-\frac{1}{3}\mathrm{ln}\left|a-\frac{1}{3}\right|+C
Comparando con las opciones, indicamos como correcta la c).
Reactivo 36
El resultado de la integral \int \left({x}^{4}-2{x}^{2}+1\right)dx es:
- \frac{{x}^{5}}{5}+{x}^{3}+x+C
- \frac{{x}^{5}}{5}-\frac{2}{3}{x}^{3}-x+C
- \frac{{x}^{5}}{5}-\frac{2}{3}{x}^{3}+x+C
- \frac{{x}^{5}}{5}+\frac{2}{3}{x}^{3}+x+C
Solución:
Para resolver integrales de funciones polinomiales, primero aplicamos la propiedad de la integral de la suma y luego la fórmula correspondiente en cada una de las integrales resultantes.
\int \left({x}^{4}-2{x}^{2}+1\right)dx=\int {x}^{4}dx-2\int {x}^{2}dx+\int dx
Aplicando las fórmulas integrales:
\int {x}^{4}dx-2\int {x}^{2}dx+\int dx=\frac{{x}^{5}}{5}-\frac{2}{3}{x}^{3}+x+C
Comparando con las opciones, indicamos como correcta la c).
Reactivo 37
Calcule el valor de la siguiente integral definida.
{\int }_{-1}^{1}{x}^{3}dx
- 1
- -1
- 4/3
- 0
Solución:
Comenzamos por calcular la primitiva del integrando para luego aplicar el teorema fundamental del cálculo. Es una potencia, por tanto, aplicamos la fórmula de integración para potencias:
{\int }_{-1}^{1}{x}^{3}dx=\left.\frac{{x}^{4}}{4}\right]\begin{array}{c}1\\ \\ -1\end{array}
Aplicando el teorema fundamental del cálculo.
\left.\frac{{x}^{4}}{4}\right]\begin{array}{c}1\\ \\ -1\end{array}=\frac{{\left(1\right)}^{4}}{4}-\frac{{\left(-1\right)}^{4}}{4}=0
Finalmente:
{\int }_{-1}^{1}{x}^{3}dx=0
La respuesta correcta se encuentra en el inciso d).
Reactivo 38
Resuelva la siguiente desigualdad absoluta.
\left|\frac{x+1}{2x-3}\right|\ge 1
- \left[\frac{2}{3},\frac{3}{2}\right)\cup \left(\frac{3}{2}, 4\right]
- \left[\frac{2}{3},\frac{3}{2}\right)
- \left(\frac{3}{2}, 4\right]
- \left[\frac{2}{3},4\right)
Solución:
Aunque esta inecuación parezca compleja, lo cierto es que debemos recordar cómo trabajar con la función valor absoluto. Por definición:
\frac{x+1}{2x-3}\le -1\cup \frac{x+1}{2x-3}\ge 1
Debemos encontrar el conjunto solución de ambas inecuaciones y luego unirlos para obtener la solución global al ejercicio. Vamos con la primera inecuación.
\frac{x+1}{2x-3}\le -1
Sumamos 1 en ambos lados.
\frac{x+1}{2x-3}+1\le 0\to \frac{x+1+2x-3}{2x-3}\le 0
\frac{3x-2}{2x-3}\le 0
Esta inecuación será menor o igual a cero cuando:
{C}_{1}:3x-2\le 0\wedge 2x-3>0
De forma contraria:
{C}_{2}:3x-2\ge 0\wedge 2x-3<0
Resolvemos a {C}_{1} .
3x-2\le 0\wedge 2x-3>0
3x\le 2\wedge 2x>3
x\le \frac{2}{3}\wedge x>\frac{3}{2}
Interceptando ambas soluciones.
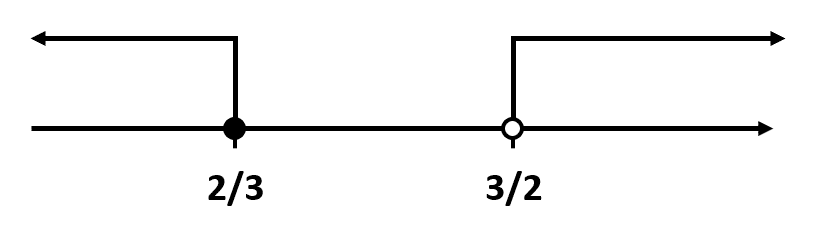
La solución es vacía: {C}_{1}=\left\{\varnothing \right\} .
Resolvemos a {C}_{2} .
3x-2\ge 0\wedge 2x-3<0
x\ge \frac{2}{3}\wedge x<\frac{3}{2}
Interceptamos:
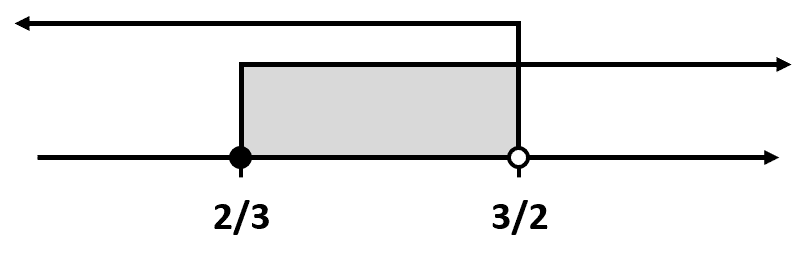
La solución es: {C}_{2}=\left[\frac{2}{3},\frac{3}{2}\right) .
Ya resolvimos la primera inecuación derivada de aplicar la definición de valor absoluto, ahora vamos con la segunda.
\frac{x+1}{2x-3}\ge 1
Restamos 1 en ambos lados.
\frac{x+1}{2x-3}-1\ge 0\to \frac{x+1-2x+3}{2x-3}\ge 0
\frac{4-x}{2x-3}\ge 0
Las condiciones para que se cumpla la desigualdad son:
{C}_{1}:4-x\ge 0\wedge 2x-3>0
De forma contraria:
{C}_{2}:4-x\le 0\wedge 2x-3<0
Resolvemos a {C}_{1} .
4-x\le 0\wedge 2x-3<0
x-4\ge 0\wedge 2x<3
x\ge 4\wedge x<\frac{3}{2}
Interceptamos.
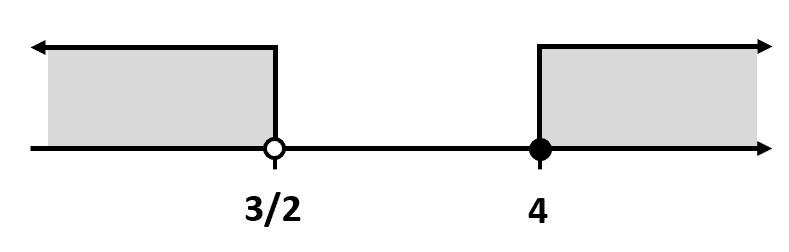
La solución es: {C}_{1}=\left\{\varnothing \right\} .
Resolvemos a {C}_{2} .
4-x\le 0\wedge 2x-3<0
x\ge 4\wedge x<\frac{3}{2}
Interceptando.
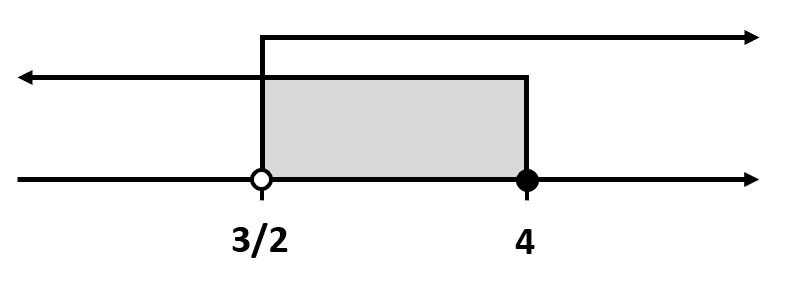
La solución es: {C}_{2}=\left(\frac{3}{2}, 4\right]
Ahora nos queda unir este resultado con el obtenido para la primera inecuación.
\left[\frac{2}{3},\frac{3}{2}\right)\cup \left(\frac{3}{2}, 4\right]
Gráficamente:
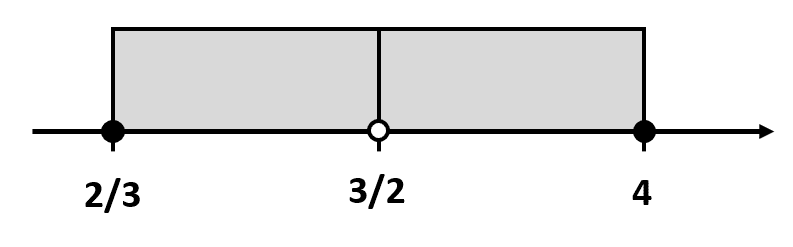
Concluimos que la respuesta correcta es el inciso a).
Reactivo 39
Calcula la derivada de la siguiente función.
y={\mathrm{tan}}^{-1}\left(\mathrm{ln}x\right)
- \frac{1}{x}\cdot \frac{1}{1+\mathrm{ln}x}
- \frac{1}{1+{\left(\mathrm{ln}x\right)}^{2}}
- -\frac{1}{x}\cdot \frac{1}{1+{\left(\mathrm{ln}x\right)}^{2}}
- \frac{1}{x}\cdot \frac{1}{1+{\left(\mathrm{ln}x\right)}^{2}}
Solución:
Cuando tenemos que calcular la derivada para funciones compuestas, es necesario emplear la regla de la cadena. En este caso, la función principal es la tangente, por lo tanto, iniciamos aplicando la fórmula para derivar correspondiente.
{y}^{\text{'}}={\left[{\mathrm{tan}}^{-1}\left(\mathrm{ln}x\right)\right]}^{\text{'}}=\frac{{\left(\mathrm{ln}x\right)}^{\text{'}}}{1+{\left(\mathrm{ln}x\right)}^{2}}
Resolvemos la derivada indicada aplicando la fórmula de la derivada del logaritmo.
\frac{{\left(\mathrm{ln}x\right)}^{\text{'}}}{1+{\left(\mathrm{ln}x\right)}^{2}}=\frac{\frac{1}{x}}{1+{\left(\mathrm{ln}x\right)}^{2}}=\frac{1}{x}\cdot \frac{1}{1+{\left(\mathrm{ln}x\right)}^{2}}
Finalmente:
{y}^{\text{'}}=\frac{1}{x}\cdot \frac{1}{1+{\left(\mathrm{ln}x\right)}^{2}}
La respuesta correcta es la d).
Reactivo 40
Escribe en lenguaje algebraico el siguiente enunciado:
El doble de x incrementado 1 es mayor o igual que cinco medios.
- 2x+1\ge \frac{5}{2}
- 2\left(x+1\right)\ge \frac{5}{2}
- 2x+1\le \frac{5}{2}
- 2x+1>\frac{5}{2}
Solución:
Para escribir la expresión del enunciado, debemos ir analizando cada frase para extraer la información correctamente. Lo primero que nos dice es que la x va multiplicada por 2 y luego se le suma 1.
El doble de x incrementado 1…
2x+1
Ahora, el operador de relación es mayor o igual seguido de la fracción \frac{5}{2} .
2x+1\ge \frac{5}{2}
Concluimos seleccionando la opción a) como respuesta correcta.


