¡Felicidades aspirante! Llegamos a la quinta y última parte del simulacro de matemáticas para el área de Ingeniería y Ciencias Físico Matemáticas del Instituto Politécnico Nacional.

Los siguientes 10 reactivos corresponden a Probabilidad y Estadística, te recomiendo repasar los temas relacionados con esta asignatura antes de pasar a los ejercicios.
Ejercicios de Matemáticas
Recuerda que puedes acceder al contenido gratuito acerca del examen en la zona IPN, con nuestros maratones de reactivos y lives resolviendo guías del examen.
Reactivo 41
A partir de la siguiente distribución de frecuencias, correspondiente al número de clientes por día que tiene un restaurante, determine el valor de la media.
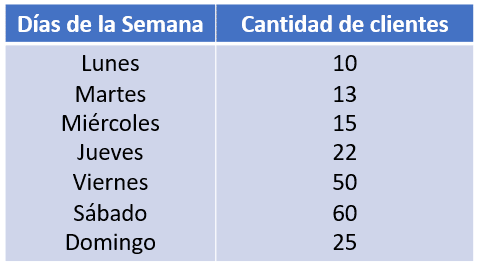
- 25
- 55
- 28
- 35
Solución:
En estadística descriptiva, la media aritmética es un valor que representa la tendencia de un conjunto de datos cuantitativos y se calcula como la sumatoria de las frecuencias absolutas de cada clase, dividida entre el total de clases.
\stackrel{-}{x}=\frac{\sum {f}_{i}}{N}
Donde N es el número de clases y \sum {f}_{i} es la sumatoria de las frecuencias absolutas de las clases. Para nosotros, el total de clases es N=7 . Sustituimos el resto de datos en la ecuación:
\stackrel{-}{x}=\frac{10+13+15+22+50+60+25}{7}=27.9
En promedio, el restaurante tiene aproximadamente 28 clientes por día.
Concluimos que la respuesta correcta es la c).
Reactivo 42
La profesora de Salud ha encomendado a sus estudiantes formar un grupo para el comité organizador de la fiesta de fin de año para la escuela. Si en la sección hay 15 estudiantes y el comité debe estar compuesto por 5 estudiantes, ¿cuántos comités diferentes se pueden formar?
- 3003
- 4003
- 5003
- 6003
Solución:
Para resolver este problema, debemos utilizar alguna de las técnicas de conteo. Lo primero que debemos determinar, es si se trata de una permutación o de una combinación. Debido a que no existe ningún rango entre los estudiantes que conformen el comité, da igual si un estudiante es seleccionado de primero o de último, por tanto, no importa el orden: empleamos combinaciones.
{C}_{5}^{15}=\frac{15!}{5!\left(15-5\right)!}
Calculando obtenemos:
{C}_{5}^{15}=3003
Se pueden formar 3003 comités de 5 integrantes con 15 estudiantes.
La respuesta correcta es el inciso a).
Reactivo 43
¿Cuántos códigos de colores 3 se pueden formar con los tonos Rojo, Azul, Verde, Amarillo, Blanco y Negro?
- 100
- 110
- 115
- 120
Solución:
Cuando hablamos de formar códigos o claves, queda sobreentendido que el orden de los elementos importa ya que, no será igual el código Azul-Rojo-Rojo que el código Rojo-Rojo-Azul. En los casos donde el orden importa, inmediatamente sabemos que se trata de una permutación/variación.
Ahora, ¿Participan todos los elementos? El enunciado nos dice que el total de colores es 6 pero que se ordenan de 3 en 3 por tanto, no participan todos los elementos: se trata de una variación.
La última pregunta que debemos responder es: ¿hay elementos repetidos? El problema nunca nos dice que no podamos repetir colores, por tanto, se trata de una Variación Ordinaria y la fórmula a utilizar es:
{V}_{3}^{6}=\frac{6!}{\left(6-3\right)!}
Calculando obtenemos:
{V}_{3}^{6}=120
Se pueden formar 120 códigos diferentes.
La respuesta correcta es el inciso d).
Reactivo 44
¿Cuál de los siguientes conjuntos corresponde a la región encerrada por una circunferencia de radio 1 y centrada en el origen?
- A=\left\{\left(x,y\right)|{x}^{2}+{y}^{2}>1\right\}
- A=\left\{\left(x,y\right)|{x}^{2}+{y}^{2}\ge 1\right\}
- A=\left\{\left(x,y\right)|{x}^{2}+{y}^{2}<1\right\}
- A=\left\{\left(x,y\right)|{x}^{2}+{y}^{2}\le 1\right\}
Solución:
Primero, recordemos cómo luce la ecuación ordinaria de una circunferencia:
{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}
En este caso, el centro es el origen y el radio 1.
{x}^{2}+{y}^{2}=1
Ahora, la región encerrada por la circunferencia son todos aquellos puntos internos al contorno cuya distancia respecto al centro es menor a 1, no estamos incluyendo al propio contorno, solo los puntos internos.
Teniendo en cuenta esto, solo debemos cambiar el signo igual por un “menor que”.
{x}^{2}+{y}^{2}<1
Finalmente, el conjunto de los puntos internos a una circunferencia de radio 1 y centrada en el origen son los que cumplen:
A=\left\{\left(x,y\right)|{x}^{2}+{y}^{2}<1\right\}
Comparando con las opciones, concluimos que la respuesta correcta está en la c).
Reactivo 45
En una encuesta hecha a los estudiantes de una preparatoria, 100 de ellos quiere estudiar alguna ingeniería y el 30% desea estudiar ingeniería electrónica. ¿Cuántos estudiantes desean estudiar una ingeniería distinta?
- 70
- 60
- 50
- 45
Solución:
Para encontrar el número de estudiantes que desea estudiar otra ingeniería, simplemente restamos el número que desea cursar ingeniería electrónica con el total, en este caso 100 estudiantes.
Calculamos el número de estudiantes de ingeniería electrónica como:
IE=100*0.3=30 \mathrm{e}\mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{s}
Ahora, restamos estos 30 estudiantes al total.
\mathrm{O}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{s}\mathrm{ }\mathrm{i}\mathrm{n}\mathrm{g}.\mathrm{ }=100-30=70\mathrm{ }\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{s}
Unos 70 estudiantes desean cursar otra ingeniería.
La respuesta correcta está en el inciso a).
Reactivo 46
En un estudio de las piezas que fabrica una máquina empapeladora, se obtuvo la siguiente tabla de datos para un turno de trabajo:
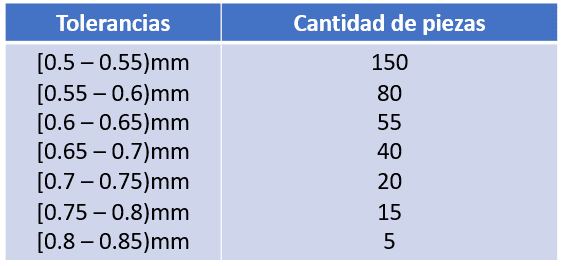
Calcule la probabilidad de obtener una pieza con el intervalo de tolerancias más alto.
- 1.37\%
- 0.137\%
- 13.7\%
- 12\%
Solución:
Recordemos la definición clásica de probabilidad:
La probabilidad de ocurrencia para un evento A es el cociente entre los sucesos favorables con A entre el total de sucesos del experimento.
A partir de la tabla sabemos que el total de piezas pertenecientes al intervalo de tolerancias más alto [0.8 – 0.85) mm es de 5 piezas. El total es igual a la suma de todas las piezas.
P\left(A\right)=\frac{5}{150+80+55+40+20+15+5}=\frac{5}{365}
P\left(A\right)=0.0137
La probabilidad es del 1.37%.
Comparando con los incisos, concluimos que la respuesta correcta se encuentra en a).
Reactivo 47
Determine el espacio muestral del siguiente experimento aleatorio:
Se lanza un dado:
- Si el resultado es menor que o igual que 3 se lanza una moneda y termina el experimento.
- Si el resultado es mayor que 3 termine el experimento súbitamente.
- \left\{1S, 2S, 3A, 4, 5, 6\right\}
- \left\{1, 2, 3, 4, 5, 6, S, A\right\}
- \left\{1S, 1A, 2S, 2A, 3A, 3S, 4, 5, 6\right\}
- \left\{1, S, 1, A, 2,S, 2,A, 3,A, 3,S, 4, 5, 6\right\}
Solución:
Debido a que el experimento está compuesto por varias fases, la forma más simple de resolverlo es desarrollar su diagrama de árbol. Comencemos con la primera tirada del dado.
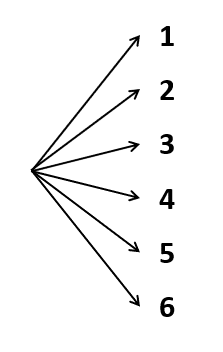
Ahora, para los resultados donde el número es menor o igual que 3, tiramos una moneda.
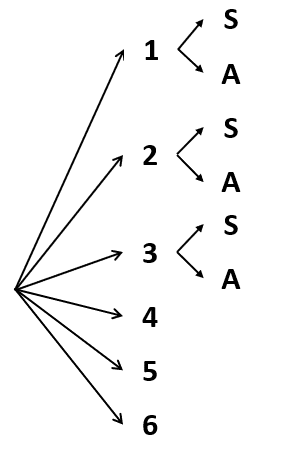
A partir del diagrama de árbol final, obtenemos el siguiente espacio muestral.
\left\{1S, 1A, 2S, 2A, 3A, 3S, 4, 5, 6\right\}
Comparando con los incisos, concluimos que la respuesta correcta es c).
Reactivo 48
Identifique cuál de los siguientes conjuntos corresponde a la resta entre el conjunto de los naturales N sin el cero y el de los números impares \left\{2n-1\right\} \forall n\ge 1 , N-\left\{2n-1\right\} .
- \left\{2, 4, 6, 8, 10, 12, 14, \dots \right\}
- \left\{0, 2, 4, 6, 8, 10, 12, 14, \dots \right\}
- \left\{2, 6, 10, 14, 18, 22, 26 \dots \right\}
- \left\{2, 4, 8, 10, 12, 14, \dots \right\}
Solución:
Primero, recordemos que la resta o diferencia de conjuntos es una operación que da como resultado los elementos del conjunto minuendo que no se encuentran en el conjunto sustraendo.
Teniendo esto en cuenta, identifiquemos cuáles son los elementos que corresponden a cada conjunto.
N=\left\{ 1, 2, 3, 4, 5, 6, \dots \right\}
\left\{2n-1\right\}=\left\{1, 3, 5, 7, 9, \dots \right\}
Expandiendo un poco los conjuntos, nos damos cuenta que la resta N-\left\{2n-1\right\} da como resultado al conjunto de los números pares.
N-\left\{2n-1\right\}=\left\{2, 4, 6, 8, 10, 12, 14, \dots \right\}
Comparando con los incisos, concluimos que la respuesta correcta se encuentra en a).
Reactivo 49
Dado el siguiente diagrama de árbol, identifique su espacio muestral.
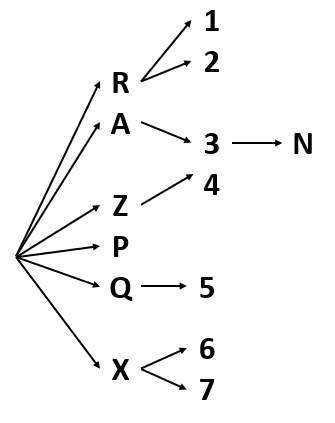
- \left\{\mathrm{R},\mathrm{ }\mathrm{A},\mathrm{ }\mathrm{Z},\mathrm{ }\mathrm{P},\mathrm{ }\mathrm{Q},\mathrm{ }\mathrm{X},\mathrm{ }1,\mathrm{ }2,\mathrm{ }3,\mathrm{ }4,\mathrm{ }5,\mathrm{ }6,\mathrm{ }7,\mathrm{ }\mathrm{N}\right\}
- \left\{1,\mathrm{ }2,\mathrm{ }\mathrm{A},\mathrm{ }\mathrm{A}3\mathrm{N},\mathrm{ }\mathrm{Z},\mathrm{ }\mathrm{Z}4,\mathrm{ }\mathrm{P},\mathrm{ }\mathrm{Q},\mathrm{ }\mathrm{Q}5,\mathrm{ }\mathrm{X},\mathrm{ }\mathrm{X}6,\mathrm{ }\mathrm{X},\mathrm{ }\mathrm{X}7\right\}
- \left\{\mathrm{R},\mathrm{ }2,\mathrm{ }\mathrm{A},\mathrm{ }3\mathrm{N},\mathrm{ }\mathrm{Z}4,\mathrm{ }\mathrm{P},\mathrm{ }\mathrm{Q}5,\mathrm{ }\mathrm{X},\mathrm{ }6,\mathrm{ }7\right\}
- \left\{\mathrm{R}1,\mathrm{ }\mathrm{R}2,\mathrm{ }\mathrm{A}3\mathrm{N},\mathrm{ }\mathrm{Z}4,\mathrm{ }\mathrm{P},\mathrm{ }\mathrm{Q}5,\mathrm{ }\mathrm{X}6,\mathrm{ }\mathrm{X}7\right\}
Solución:
Para establecer el espacio muestral expresado a partir del diagrama de árbol, debemos recorrer cada una de las ramas del diagrama hasta llegar a la última hoja. Las ramas son las flechas y las hojas los datos o eventos.
En la siguiente imagen te muestro el recorrido completo del diagrama de árbol.
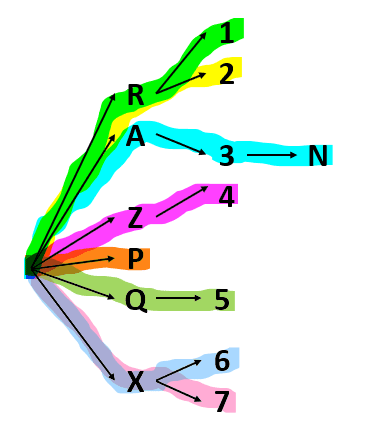
Siguiendo cada una de las franjas de colores, obtenemos los elementos del espacio muestral.
\left\{\mathrm{R}1,\mathrm{ }\mathrm{R}2,\mathrm{ }\mathrm{A}3\mathrm{N},\mathrm{ }\mathrm{Z}4,\mathrm{ }\mathrm{P},\mathrm{ }\mathrm{Q}5,\mathrm{ }\mathrm{X}6,\mathrm{ }\mathrm{X}7\right\}
Comparando con las opciones, concluimos que la respuesta correcta es la d).
Reactivo 50
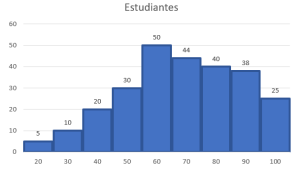
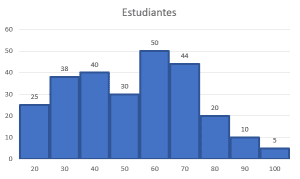
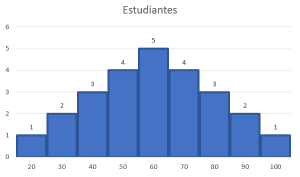
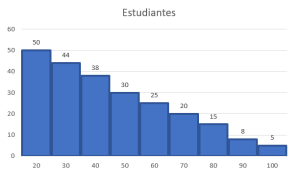
Dada la siguiente tabla de frecuencias, identifique cuál de los siguientes histogramas corresponde con los datos suministrados.
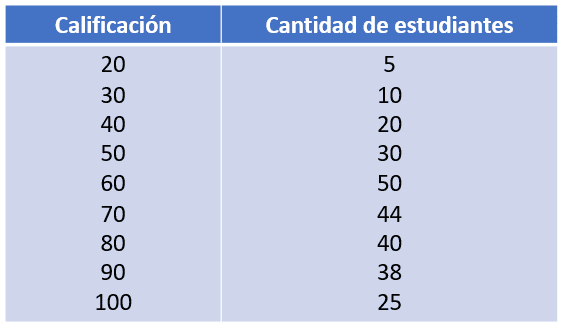
Solución:
Para encontrar la respuesta correcta a este problema, debemos examinar dos cosas en los histogramas de frecuencia de los incisos:
- Que el eje horizontal concuerde con las calificaciones desde el 20 hasta el 100.
- Y que las barras tengan la altura correspondiente a la cantidad de estudiantes que lograron dicha calificación.
El único que cumple con ambas es el del inciso a), ya que el resto tiene bien el eje horizontal, pero valores distintos para la altura de las barras.
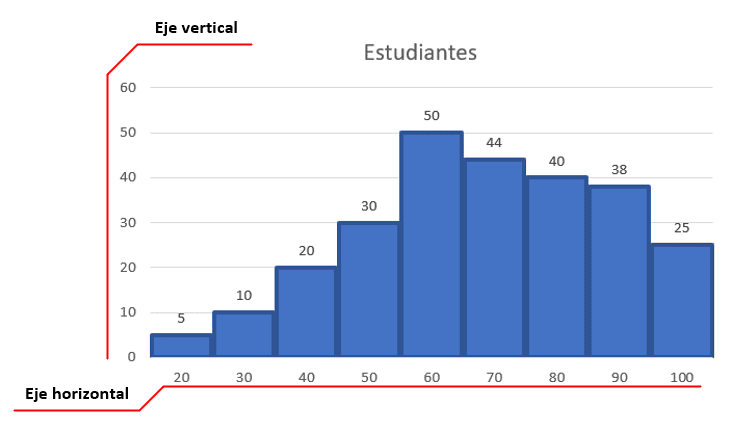
Concluimos indicando como correcta a la opción a).