Examen Simulador IPN Física: Ciencias Médico Biológicas P.2

Continuamos resolviendo el examen simulador de física del IPN para el área de ciencias médico biológicas, ahora vamos con los reactivos del 11 al 20.

Reactivo 11

Si la relación de dinas a Newtons es 1 \mathrm{N}={10}^{5} \mathrm{d}\mathrm{i}\mathrm{n}\mathrm{a} y a su vez, la relación entre libras y Newtons es 1 \mathrm{l}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{a}=4.448\mathrm{ }\mathrm{N} , ¿cuál es la relación entre dinas y libras?

1. 4.448 \mathrm{l}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{a}={10}^{5} \mathrm{d}\mathrm{i}\mathrm{n}\mathrm{a}
2. 4.448\cdot {10}^{5} \mathrm{l}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{a}=1 \mathrm{d}\mathrm{i}\mathrm{n}\mathrm{a}
3. 1 \mathrm{l}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{a}=4.448 \mathrm{d}\mathrm{i}\mathrm{n}\mathrm{a}
4. 1 \mathrm{l}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{a}=4.448\cdot {10}^{5} \mathrm{d}\mathrm{i}\mathrm{n}\mathrm{a}

Solución:

En este caso, debemos aplicar los factores de equivalencia entre las unidades, de tal forma que eliminemos Newtons y solo nos queden libras y dinas. Comenzamos diciendo que:

1 \mathrm{l}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{a}=4.448\mathrm{ }\mathrm{N}

Ahora, aplicamos el factor \frac{{10}^{5} \mathrm{d}\mathrm{i}\mathrm{n}\mathrm{a}}{1 \mathrm{N}} para eliminar Newtons y que solo queden dinas.

1 \mathrm{l}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{a}=4.448\mathrm{ }\mathrm{N}\cdot \frac{{10}^{5} \mathrm{d}\mathrm{i}\mathrm{n}\mathrm{a}}{1 \mathrm{N}}=4.448\cdot {10}^{5} \mathrm{d}\mathrm{i}\mathrm{n}\mathrm{a}

Concluimos entonces que:

1 \mathrm{l}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{a}=4.448\cdot {10}^{5} \mathrm{d}\mathrm{i}\mathrm{n}\mathrm{a}

Comparando con los incisos, concluimos que la respuesta correcta está en d).

Reactivo 12

Calcule la magnitud del vector perpendicular al plano que forman \overrightarrow{u}=\left(1, -2, 1\right) y \overrightarrow{v}=\left(0, 3, -1\right) .

1. \sqrt{7}
2. \sqrt{8}
3. \sqrt{10}
4. \sqrt{11}

Solución:

El vector que es perpendicular al plano que forman otros dos se obtiene a través del producto vectorial.

Ahora, el producto vectorial puede hacerse de dos formas: \overrightarrow{u}\times \overrightarrow{v} y \overrightarrow{v}\times \overrightarrow{u} , ambos vectores resultantes serán perpendiculares, tendrán la misma magnitud, pero apuntan en direcciones opuestas.

En este caso, solo nos interesa la magnitud, por tanto, será indiferente el orden de los vectores.

\overrightarrow{w}=\left|\overrightarrow{u}\times \overrightarrow{v}\right|=\left|\overrightarrow{v}\times \overrightarrow{u}\right|

Calculamos primero el producto vectorial.

\overrightarrow{w}=\overrightarrow{u}\times \overrightarrow{v}=\left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ 1& -2& 1\\ 0& 3& -1\end{array}\right|

\overrightarrow{w}=\left|\begin{array}{cc}-2& 1\\ 3& -1\end{array}\right|\widehat{i}-\left|\begin{array}{cc}1& 1\\ 0& -1\end{array}\right|\widehat{j}+\left|\begin{array}{cc}1& -2\\ 0& 3\end{array}\right|\widehat{j}

Calculamos los determinantes en cada caso.

\overrightarrow{w}=\left(2-3\right)\widehat{i}-\left(-1-0\right)\widehat{j}+\left(3-0\right)\widehat{j}=-\widehat{i}+\widehat{j}+3\widehat{j}

\overrightarrow{w}=-\widehat{i}+\widehat{j}+3\widehat{j}

Ahora, calculamos el módulo del vector.

\left|\overrightarrow{w}\right|=\left|-\widehat{i}+\widehat{j}+3\widehat{j}\right|=\sqrt{{\left(-1\right)}^{2}+{1}^{2}+{3}^{2}}=\sqrt{11}

Finalmente, el módulo del vector perpendicular es:

\left|\overrightarrow{w}\right|=\sqrt{11}

Comparando con los incisos, indicamos como correcto al d).

Reactivo 13

Calcule la magnitud de la fuerza que debe aplicarse al bloque de masa 5 \mathrm{k}\mathrm{g} para que permanezca estático. Considere el ángulo de acción de la fuerza igual a 45°, que no existe fricción y la gravedad g=9.8 \mathrm{m}/{\mathrm{s}}^{2} .

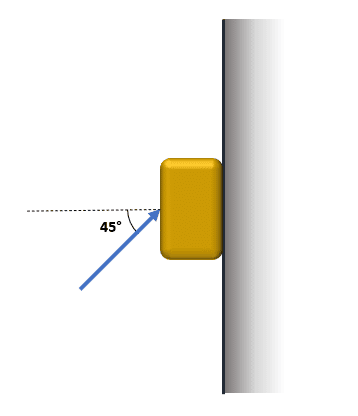
1. 49.3 \mathrm{N}
2. 69.3 \mathrm{N}
3. 79.3 \mathrm{N}
4. 59.3 \mathrm{N}

Solución:

En este caso, nuestra intención es mantener al bloque perfectamente estático y pegado a la pared. Comencemos por dibujar el Diagrama de Cuerpo Libre del cuerpo.

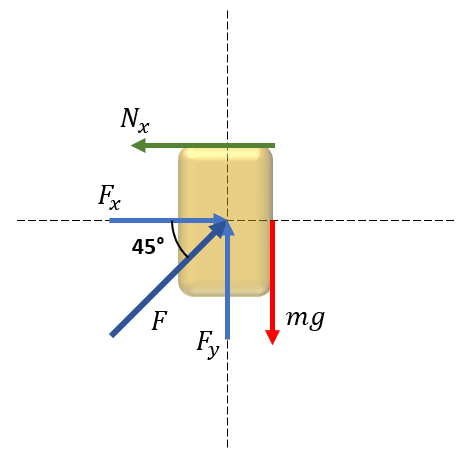
En este caso, no nos importa las fuerzas sobre el eje x sino las componentes sobre el eje y .

\sum {F}_{y}=0\to {F}_{y}-mg=0

Además, sabemos que {F}_{y} puede obtenerse como:

{F}_{y}=F\mathrm{sin}45=\frac{\sqrt{2}}{2}F

Sustituimos y despejamos a F .

\frac{\sqrt{2}}{2}F=mg\to F=\frac{2}{\sqrt{2}}mg

F=\frac{2}{\sqrt{2}}\left(5 \mathrm{k}\mathrm{g}\right)\left(9.8 \mathrm{m}/\mathrm{s}\right)=69.3 \mathrm{N}

La magnitud de la fuerza debe ser igual a 69.3 Newtons.

Comparando con las opciones, indicamos como correcta la b).

Reactivo 14

A partir del sistema que se muestra en la figura, determine la relación entre las masas para que se cumpla el equilibrio mecánico.

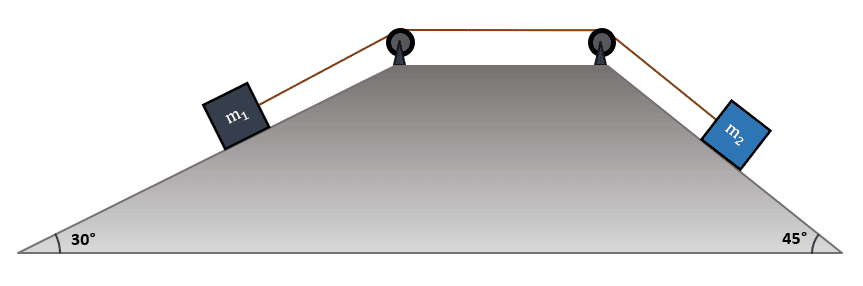
1. \frac{\sqrt{3}}{2}
2. 2
3. \sqrt{2}
4. \frac{1}{2}

Solución:

Aunque el sistema parezca complejo, el esquema que debemos seguir para su solución es: identificamos las condiciones de equilibrio que debemos aplicar y descomponemos las fuerzas sobre los cuerpos mediante diagramas de cuerpo libre.

Debido a que ninguno de los cuerpos rota, descartamos las ecuaciones de equilibrio frente a torcas, solo queda examinar el equilibrio respecto a fuerzas. Comencemos a examinar la masa {m}_{1} .

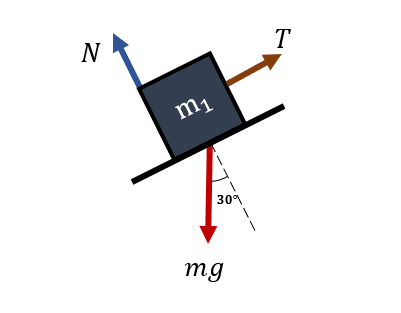
En ninguna de las dos masas nos interesan las ecuaciones respecto a la vertical porque en dicha dirección no ocurre movimiento. Descomponemos al peso sobre el eje x como {P}_{x}={m}_{1}g\mathrm{sin}30 y sustituimos en la ecuación de equilibrio correspondiente.

\sum {F}_{x}=0\to T-{m}_{1}g\mathrm{sin}30=0

Despejamos a la tensión:

T={m}_{1}g\mathrm{sin}30

Vamos ahora con el segundo bloque.

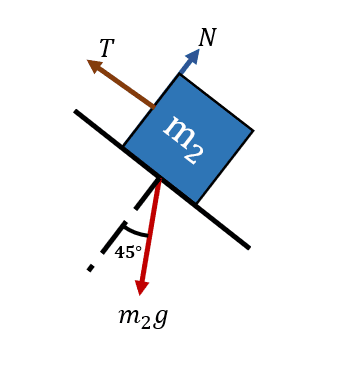
Descomponemos sobre el eje x el peso y aplicamos la condición de equilibrio sobre dicho eje.

\sum {F}_{x}=0\to {m}_{2}g\mathrm{sin}45-T=0

Despejamos a T .

T={m}_{2}g\mathrm{sin}45

Igualamos las ecuaciones:

{m}_{2}g\mathrm{sin}45={m}_{1}g\mathrm{sin}30

Finalmente decimos que:

\frac{{m}_{1}}{{m}_{2}}=\frac{\mathrm{sin}30}{\mathrm{sin}45}=\frac{\sqrt{2}}{2}

Esta relación nos dice que la masa {m}_{1} debe ser \frac{\sqrt{2}}{2} veces la masa {m}_{2} .

Concluimos indicando como respuesta correcta la opción c).

Reactivo 15

Para eliminar parte del sesgo cognitivo en los investigadores de un experimento de 5 años, la directiva decidió cambiar las unidades de medición, de tal forma que cada uno de los 4 integrantes de la junta estableció una unidad equivalente para: el tiempo, la masa, la carga eléctrica y la longitud.

En la siguiente tabla se muestran las constantes de equivalencia:

Si la medición final del potencial que permite reconstruir la trayectoria del neutrino es 12.36478\frac{{\mathrm{P}}^{2}\cdot \mathrm{k}\mathrm{f}}{{\mathrm{t}\mathrm{q}}^{3}\cdot \mathrm{T}\mathrm{k}} , ¿cuál es la medición real del detector?

1. 0.2686\times {10}^{26}\frac{{\mathrm{m}}^{2}\cdot \mathrm{k}\mathrm{g}}{{\mathrm{s}}^{3}\cdot \mathrm{A}}
2. 0.002686\times {10}^{26}\frac{{\mathrm{m}}^{2}\cdot \mathrm{k}\mathrm{g}}{{\mathrm{s}}^{3}\cdot \mathrm{A}}
3. 0.02686\times {10}^{26}\frac{{\mathrm{m}}^{2}\cdot \mathrm{k}\mathrm{g}}{{\mathrm{s}}^{3}\cdot \mathrm{A}}
4. 2.686\times {10}^{26}\frac{{\mathrm{m}}^{2}\cdot \mathrm{k}\mathrm{g}}{{\mathrm{s}}^{3}\cdot \mathrm{A}}

Solución:

Aunque el enunciado pueda parecer complejo, lo cierto es que estamos frente a un problema de conversión de unidades. Simplemente debemos convertir cada unidad del sistema inventado por los investigadores, el sistema internacional de unidades a partir de la tabla.

Comencemos por convertir de Planks a metros.

12.36478\frac{{\mathrm{P}}^{2}\cdot \mathrm{k}\mathrm{f}}{{\mathrm{t}\mathrm{q}}^{3}\cdot \mathrm{T}\mathrm{k}}\cdot \frac{1 {\mathrm{m}}^{2}}{{10}^{-48} {\mathrm{P}}^{2}}

Cancelando {\mathrm{P}}^{2} con {\mathrm{P}}^{2} nos queda:

=12.36478\times {10}^{48}\frac{{\mathrm{m}}^{2}\cdot \mathrm{k}\mathrm{f}}{{\mathrm{t}\mathrm{q}}^{3}\cdot \mathrm{T}\mathrm{k}}

Ahora eliminamos kilofestos por kilogramos.

12.36478\times {10}^{48}\frac{{\mathrm{m}}^{2}\cdot \mathrm{k}\mathrm{f}}{{\mathrm{t}\mathrm{q}}^{3}\cdot \mathrm{T}\mathrm{k}}\cdot \frac{4.5 \mathrm{k}\mathrm{g}}{33.58 \mathrm{k}\mathrm{f}}

Dividiendo 12.36478 con 33.58 nos queda:

=0.3682\times {10}^{48}\frac{{\mathrm{m}}^{2}\cdot \mathrm{k}\mathrm{g}}{{\mathrm{t}\mathrm{q}}^{3}\cdot \mathrm{T}\mathrm{k}}

Convertimos taquidos a segundos.

0.3682\times {10}^{48}\frac{{\mathrm{m}}^{2}\cdot \mathrm{k}\mathrm{g}}{{\mathrm{t}\mathrm{q}}^{3}\cdot \mathrm{T}\mathrm{k}}\cdot \frac{0.064\times {10}^{-18}\mathrm{ }{\mathrm{t}\mathrm{q}}^{3}}{1 {\mathrm{s}}^{3}}

Simplificando nos queda:

=0.02356\times {10}^{30}\frac{{\mathrm{m}}^{2}\cdot \mathrm{k}\mathrm{g}}{{\mathrm{s}}^{3}\cdot \mathrm{T}\mathrm{k}}

Finalmente, pasamos de Tektrons a Amperios.

0.02356\times {10}^{30}\frac{{\mathrm{m}}^{2}\cdot \mathrm{k}\mathrm{g}}{{\mathrm{s}}^{3}\cdot \mathrm{T}\mathrm{k}}\cdot \frac{{1.14\times 10}^{-4}\mathrm{ }\mathrm{T}\mathrm{k}}{1 \mathrm{A}}

Simplificando:

=0.02686\times {10}^{26}\frac{{\mathrm{m}}^{2}\cdot \mathrm{k}\mathrm{g}}{{\mathrm{s}}^{3}\cdot \mathrm{A}}

Comparando con los incisos, concluimos que la respuesta correcta es el c).

Reactivo 16

Si la densidad de una sustancia es de 876\mathrm{ }\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} y ocupa un volumen de 0.015 metros cúbicos, ¿cuál es la masa de la sustancia?

1. 13.14 \mathrm{k}\mathrm{g}
2. 22.4 \mathrm{k}\mathrm{g}
3. 23.14 \mathrm{k}\mathrm{g}
4. 33.4 \mathrm{k}\mathrm{g}

Solución:

Para obtener la masa de la sustancia, simplemente debemos multiplicar el volumen que ocupa por su densidad.

m=876\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}}\cdot 0.015 {\mathrm{m}}^{3}=13.14 \mathrm{k}\mathrm{g}

Comparando con los incisos, la respuesta correcta está en el a).

Reactivo 17

A partir de la siguiente gráfica correspondiente al movimiento rectilíneo de dos coches A y B , identifique:

1. La rapidez de cada uno
2. ¿Cuánto tiempo tardan en encontrarse?

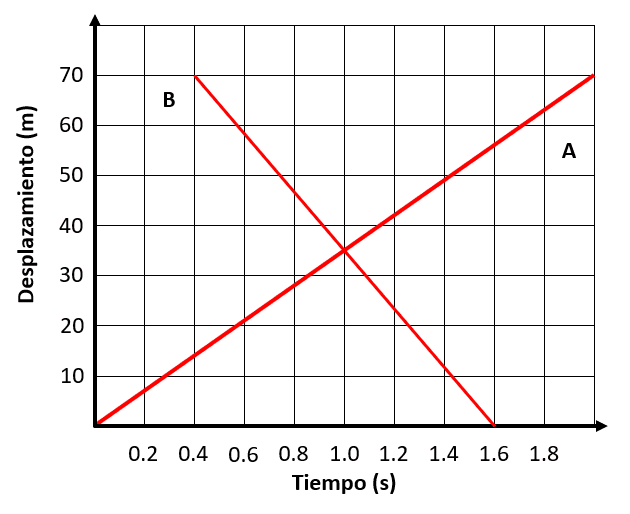
1. {v}_{A}=35 \mathrm{m}/\mathrm{s} , {v}_{B}=58.3 \mathrm{m}/\mathrm{s} y t=0.8 \mathrm{s}
2. {v}_{A}=35 \mathrm{m}/\mathrm{s} , {v}_{B}=-58.3 \mathrm{m}/\mathrm{s} y t=1 \mathrm{s}
3. {v}_{A}=35 \mathrm{m}/\mathrm{s} , {v}_{B}=58.3 \mathrm{m}/\mathrm{s} y t=1 \mathrm{s}
4. {v}_{A}=-35 \mathrm{m}/\mathrm{s} , {v}_{B}=58.3 \mathrm{m}/\mathrm{s} y t=1 \mathrm{s}

Solución:

Para responder las dos preguntas que nos hace el enunciado, debemos primero identificar el tipo de gráfica que nos indica y el movimiento que sigue cada uno de los cuerpos.

Examinando los ejes coordenados, veremos que en el eje de las abscisas se encuentra el tiempo y en el de las ordenadas el desplazamiento, es una gráfica de desplazamiento en función del tiempo.

Ahora, ya que las curvas de desplazamiento de los cuerpos son líneas rectas, esto nos dice que el movimiento que experimentan ambas es uniforme y con rapidez constante, es decir un MRU. Para calcular la rapidez, simplemente utilizamos la siguiente ecuación:

v=\frac{{d}_{2}-{d}_{1}}{{t}_{2}-{t}_{1}}

Para el cuerpo A .

{v}_{A}=\frac{70\mathrm{m}-0\mathrm{m}}{2\mathrm{s}-0\mathrm{s}}=35 \mathrm{m}/\mathrm{s}

Para el cuerpo B .

{v}_{B}=\frac{0\mathrm{m}-70\mathrm{m}}{1.6\mathrm{s}-0.4\mathrm{s}}=58.3 \mathrm{m}/\mathrm{s}

Aunque para el segundo cuerpo el resultado sea negativo, la rapidez siempre se escribe positiva porque corresponde al módulo de la velocidad. La única que lleva signo en este caso es la velocidad.

Para la segunda pregunta, simplemente tomamos el tiempo desde que comienza el movimiento en la escala hasta que las dos rectas se crucen. Esto ocurre para t=1 \mathrm{s} . Expresamos el resultado como:

{v}_{A}=35 \mathrm{m}/\mathrm{s} , {v}_{B}=58.3 \mathrm{m}/\mathrm{s} y t=1 \mathrm{s} .

Comparando con los incisos, indicamos como correcta la opción c).

Reactivo 18

Calcule la fuerza centrípeta que experimenta una partícula puntual con una masa de 2 \mathrm{k}\mathrm{g} , que gira alrededor de un eje fijo a una distancia de 0.25 metros a una velocidad angular la 2 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} .

1. 1 Newton
2. 5 Newton
3. 2 Newton
4. 5 Newton

Solución:

Siguiendo la definición de la segunda Ley de Newton, sabemos que la magnitud de la fuerza resultante que experimenta un cuerpo es igual al producto de su masa por su aceleración.

F=ma

En el movimiento circular, la fuerza centrípeta se puede calcular a partir de la aceleración centrípeta.

{a}_{c}=\frac{{v}^{2}}{r}=r{w}^{2}

En este caso, tenemos como dato la velocidad angular w=2 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} y el radio de giro r=0.25 \mathrm{m} .

{a}_{c}=\left(0.25 \mathrm{m}\right){\left(2 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}\right)}^{2}=0.5 \mathrm{m}/{\mathrm{s}}^{2}

Sustituimos en la ecuación de fuerza:

{F}_{c}=\left(2 \mathrm{k}\mathrm{g}\right)\left(0.5 \mathrm{m}/{\mathrm{s}}^{2}\right)=1 \mathrm{N}

La fuerza centrípeta experimentada es de 1 Newton.

Concluimos que la respuesta correcta es la a).

Reactivo 19

Un bloque de 5 kilogramos de masa se sumerge en una sustancia de densidad desconocida y flota quedando parcialmente sumergido. Si el volumen desplazado es de 0.004 metros cúbicos, calcule la densidad del fluido.

1. 1250 \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}
2. 125 \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}
3. 12.5 \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}
4. 12500 \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}

Solución:

Para resolver este problema, debemos hacer uso del principio de Arquímedes, el cual nos dice:

Al sumergir un cuerpo total o parcialmente en un líquido, podemos notar que una parte del líquido es desplazado y que empuja con una fuerza hacia arriba, ocasionando que el cuerpo experimente una pérdida aparente de peso.

Esto puede escribirse algebraicamente como:

E={\rho }_{L}g{V}_{d}

Debido a que el cuerpo queda suspendido en el líquido, podemos decir que la fuerza de empuje vence por completo al peso del objeto.

mg={\rho }_{L}g{V}_{d}

Despejamos la densidad del líquido.

{\rho }_{L}=\frac{m}{{V}_{d}}=\frac{5 \mathrm{k}\mathrm{g}}{0.004 {\mathrm{m}}^{3}}=1250 \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}

Concluimos seleccionando como correcta la a).

Reactivo 20

Un proyectil es disparado desde la cima de una montaña con un ángulo respecto a la vertical de 0°. Si la velocidad inicial es de 15 m/s, ¿cuál es la distancia horizontal que alcanza el cuerpo si la montaña mide 25 metros de altura?

Considere g=10 \mathrm{m}/{\mathrm{s}}^{2} .

1. 6 m
2. 54 m
3. 57 m
4. 6 m

Solución:

En el movimiento de proyectiles, el desplazamiento horizontal de los cuerpos (en ausencia de fuerzas externas) corresponde a un movimiento rectilíneo uniforme.

{x}_{f}={x}_{o}+{v}_{x}t

Para encontrar el desplazamiento horizontal total, debemos calcular la velocidad horizontal y el tiempo de vuelo del proyectil. Debido a que el disparo es totalmente horizontal, la velocidad inicial vertical es cero {v}_{oy}=0 \mathrm{m}/\mathrm{s} mientras que la velocidad {v}_{x}=15 \mathrm{m}/\mathrm{s} .

El tiempo de vuelo será el que tarda en caer los 25 metros.

{y}_{f}={y}_{o}+{v}_{oy}t-\frac{g{t}^{2}}{2}

Sustituimos {y}_{f}=0 \mathrm{m} , {y}_{o}=25 \mathrm{m} y {v}_{oy}=0\mathrm{ }\mathrm{m}/\mathrm{s} .

0=25-\frac{10{t}^{2}}{2}\to 5{t}^{2}=25

t=\sqrt{5} \mathrm{s}=2.236 \mathrm{s}

Ahora calculamos el desplazamiento horizontal total.

{x}_{f}=0+\left(15\right)\left(2.236\right)=33.54 \mathrm{m}

El proyectil se desplaza 33.54 metros en la horizontal.

La respuesta correcta es el inciso b).