¡Hola de nuevo aspirante! En este post vamos a resolver los ejercicios del 31 al 40, correspondientes a la cuarta parte del simulacro de matemáticas para el examen de ingreso al IPN en el área de Ciencias Médico Biológicas.

Recuerda resolver los ejercicios por tu cuenta antes de revisar la respuesta. Además, revisa el temario y estudia los fundamentos de cada uno
Ejercicios de Matemáticas
Continuamos con los siguientes 10 reactivos del simulacro de matemáticas, de cara a la prueba de ingreso del Instituto Politécnico Nacional en el área de las Ciencias Médico Biológicas.
Reactivo 31
Obtenga la integral que permite calcular la longitud de arco para la curva y=\mathrm{ln}x , desde x=1 hasta x=2 .
- L={\int }_{1}^{2}\frac{x}{\sqrt{1+{x}^{2}}}dx
- L={\int }_{2}^{1}\frac{\sqrt{1+{x}^{2}}}{x}dx
- L={\int }_{1}^{2}\frac{\sqrt{1-{x}^{2}}}{x}dx
- L={\int }_{1}^{2}\frac{\sqrt{1+{x}^{2}}}{x}dx
Solución:
Para calcular la longitud de cualquier curva plana, es necesario aplicar una de las siguientes ecuaciones integrales:
L={\int }_{{x}_{1}}^{{x}_{2}}\sqrt{1+{f}^{\text{'}}{\left(x\right)}^{2}}dx
L={\int }_{{y}_{1}}^{{y}_{2}}\sqrt{1+{f}^{\text{'}}{\left(y\right)}^{2}}dy
Escoger una de ellas dependerá de la complejidad que tenga la curva respecto a cada variable y lo sencillo que resulte la integral. En nuestro caso, la curva dada no representa mayor problema si la integramos respecto a x , por tanto, pasamos a calcular su derivada.
{y}^{\text{'}}={f}^{\text{'}}\left(x\right)=\frac{1}{x}
Sustituimos tanto a la función como a los límites de integración.
L={\int }_{1}^{2}\sqrt{1+{\left(\frac{1}{x}\right)}^{2}}dx
Simplificando y ordenando el integrando nos queda:
L={\int }_{1}^{2}\frac{\sqrt{1+{x}^{2}}}{x}dx
Gráficamente, esta integral nos permite calcular la longitud de x=1 a x=2 de la curva y=\mathrm{ln}x .
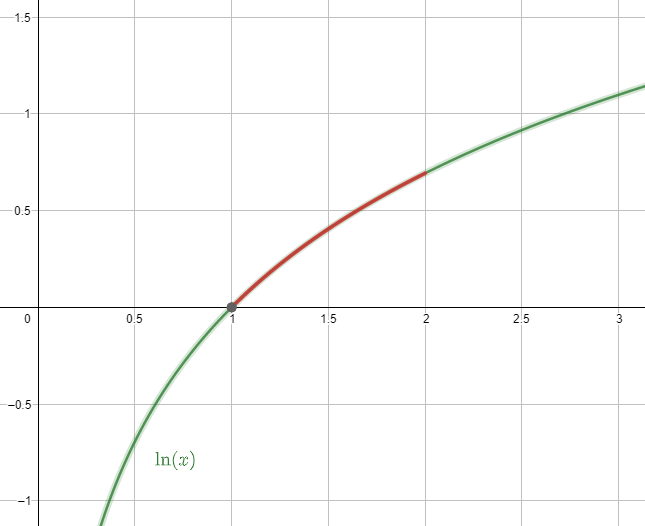
Concluyendo el ejercicio, indicamos como respuesta correcta la opción d).
Reactivo 32
Al resolver la integral \int x\mathrm{sin}\left({x}^{2}+1\right)dx se obtiene:
- -\frac{1}{2}\mathrm{sin}\left({x}^{2}+1\right)+C
- \mathrm{cos}\left({x}^{2}+1\right)+C
- \frac{1}{2}\mathrm{cos}\left({x}^{2}+1\right)+C
- -\frac{1}{2}\mathrm{cos}\left({x}^{2}+1\right)+C
Solución:
Para resolver cualquier integral, debemos analizar la función integrando, de tal forma que consigamos indicios del método y los artificios matemáticos que deberíamos aplicar. Es claro que no es una integral inmediata, porque ninguna tabla la contiene.
Una característica que es de notar y que nos ayudará a encontrar su solución, es que la x fuera del argumento del seno puede convertirse en la derivada de {x}^{2}+1 . Por tanto, debemos aplicar el cambio de variables.
u={x}^{2}+1\to du=2xdx
Pasamos el 2 a dividir.
\frac{1}{2}du=xdx
El diferencial xdx se encuentra en nuestra integral original, por tanto, es posible efectuar el cambio.
\int x\mathrm{sin}\left({x}^{2}+1\right)dx\to \frac{1}{2}\int \mathrm{sin}udu
Esta integral si es inmediata. Aplicamos su fórmula correspondiente.
\frac{1}{2}\int \mathrm{sin}udu=-\frac{1}{2}\mathrm{cos}u+C
Devolvemos el cambio de variables.
I=-\frac{1}{2}\mathrm{cos}\left({x}^{2}+1\right)+C
Comparando con las opciones del problema, indicamos como respuesta correcta al inciso c).
Reactivo 33
En la siguiente integral, es necesario aplicar un cambio trigonométrico para simplificar su solución, indique cuál de los siguientes cambios permite resolver la integral.
\int \frac{\mathrm{cos}x}{{\mathrm{sin}}^{2}x}dx
- \mathrm{csc}x\mathrm{tan}x
- \mathrm{csc}x\mathrm{ctg}x
- \mathrm{sec}x\mathrm{tan}x
- \mathrm{sec}x\mathrm{csc}x
Solución:
Muchas de las integrales trigonométricas, realmente consisten en aplicar transformaciones a las expresiones originales, de tal forma que podamos llegar a una integral más sencilla y, en el mejor de los casos, inmediata.
Comencemos por factorizar el {\mathrm{sin}}^{2}x .
\int \frac{\mathrm{cos}x}{{\mathrm{sin}}^{2}x}dx=\int \frac{\mathrm{cos}x}{\mathrm{sin}x\cdot \mathrm{sin}x}dx
Separamos la fracción como el producto de dos fracciones.
\int \frac{\mathrm{cos}x}{\mathrm{sin}x\cdot \mathrm{sin}x}dx=\int \frac{\mathrm{cos}x}{\mathrm{sin}x}\cdot \frac{1}{\mathrm{sin}x}dx
Aplicamos las identidades: \frac{\mathrm{cos}x}{\mathrm{sin}x}=\mathrm{cot}x y \frac{1}{\mathrm{sin}x}=\mathrm{csc}x .
\int \frac{\mathrm{cos}x}{\mathrm{sin}x}\cdot \frac{1}{\mathrm{sin}x}dx=\int \mathrm{cot}x\cdot \mathrm{csc}xdx
Esta integral es inmediata, hemos encontrado la transformación que simplifica al integrando. Ten en cuenta que pudimos seguir otros caminos, como sustituir {\mathrm{sin}}^{2}x=1-{\mathrm{cos}}^{2}x , pero esto no nos habría simplificado la solución.
Parte de resolver este tipo de problemas pasa por tener mucha práctica para ir intuyendo qué cambios pueden o no ser favorables. Concluimos que la respuesta correcta se encuentra en el inciso b).
Reactivo 34
El resultado de calcular la integral indefinida \int \frac{2}{x+1}dx es:
- 2\mathrm{ln}\left(x\right)+C
- 2\mathrm{ln}\left(x-1\right)+C
- \mathrm{ln}\left(x\right)+C
- 2\mathrm{ln}\left(x+1\right)+C
Solución:
Para resolver esta integral, podríamos vernos tentados a aplicar cambio de variables, pero la verdad es que la derivada de x+1 es 1, por tanto, estaríamos sumando pasos innecesarios a la solución. En su lugar, comencemos por extraer la constante del integrando.
\int \frac{2}{x+1}dx=2\int \frac{1}{x+1}d\left(x+1\right)
Examinando la integral y teniendo en cuenta las fórmulas inmediatas, en este caso debemos aplicar:
\int \frac{1}{u}du=\mathrm{ln}u+C
El resultado sería:
2\int \frac{1}{x+1}d\left(x+1\right)=2\mathrm{ln}\left(x+1\right)+C
Comparando con las opciones, concluimos que la respuesta correcta es la opción d).
Reactivo 35
Calcular la siguiente integral indefinida.
\int \left(\frac{2}{{x}^{2}}-2x+\sqrt{x+1}\right)dx- -\frac{2}{x}-{x}^{2}+\frac{2}{3}(x+1{)}^{\frac{3}{2}}+C
- \frac{2}{x}+{x}^{2}-\frac{2}{3}(x+1{)}^{\frac{3}{2}}+C
- -\frac{1}{x}-{x}^{2}+(x+1{)}^{\frac{3}{2}}+C
- -2\mathrm{ln}\left(x\right)-{x}^{2}+\frac{2}{3}(x+1{)}^{\frac{3}{2}}+C
Solución:
Esta integral parece compleja a simple vista, pero luego de aplicar la propiedad de la integral de la suma, nos daremos cuenta que realmente se trata de 3 integrales inmediatas.
\int \left(\frac{2}{{x}^{2}}-2x+\sqrt{x+1}\right)dx=\int \frac{2}{{x}^{2}}dx-\int 2xdx+\int \sqrt{x+1}dx
Para la primera integral, aplicamos la propiedad del exponente negativo.
\int 2{x}^{-2}dx-\int 2xdx+\int \sqrt{x+1}dx
Ahora, vemos como las 3 integrales son inmediatas. Debemos tener en cuenta que la derivada de x+1 es 1, por tanto, no es necesario aplicar cambio de variables. En las tres integrales empleamos la fórmula de la integral de una potencia.
\int 2{x}^{-2}dx-\int 2xdx+\int {\left(x+1\right)}^{\frac{1}{2}} dx=-\frac{2}{x}-{x}^{2}+\frac{2}{3}{\left(x+1\right)}^{\frac{3}{2}}+C
Comparando nuestra respuesta con los incisos, concluimos que la opción correcta es la a).
Reactivo 36
¿Cuál es el desarrollo en fracciones parciales del siguiente cociente?
\frac{{x}^{2}-1}{2x\left(3x-2\right)\left(x-1\right)\left(2x+3\right)}
- -\frac{1}{12x}+\frac{15}{52(3x-2)}-\frac{1}{39(2x+3)}
- -\frac{1}{12x}+\frac{15}{52(3x-2)}-\frac{1}{(2x+3)}
- -\frac{1}{12x}+\frac{1}{(3x-2)}-\frac{1}{39(2x+3)}
- \frac{1}{12x}-\frac{15}{52\left(3x-2\right)}+\frac{1}{39(2x+3)}
Solución:
Antes de resolver cualquier separación en fracciones parciales, debemos intentar factorizar el numerador (si no es demasiado complicado) para ver si podemos simplificar algún factor con los factores del denominador.
\frac{\left(x+1\right)\left(x-1\right)}{2x\left(3x-2\right)\left(x-1\right)\left(2x+3\right)}=\frac{x+1}{2x\left(3x-2\right)\left(2x+3\right)}
Ahora, tal como dice el procedimiento para separar en fracciones parciales, igualamos la fracción a una suma de fracciones cuyos denominadores son los factores 2x , \left(3x-2\right) y \left(2x+3\right) , donde los numeradores serán constantes desconocidos.
\frac{x+1}{2x\left(3x-2\right)\left(2x+3\right)}=\frac{A}{2x}+\frac{B}{3x-2}+\frac{C}{2x+3}
Pasamos a multiplicar el denominador de la izquierda.
x+1=A\left(3x-2\right)\left(2x+3\right)+2Bx\left(2x+3\right)+2Cx\left(3x-2\right)
En este punto tenemos dos opciones: a) desarrollamos todos los productos, igualamos términos semejantes y formamos un SEL o b) sustituimos valores de tal forma que se eliminen ciertos términos para calcular directamente A , B y C . Debido a que el desarrollo no es tan laborioso, recurriremos a la primera opción.
x+1=A\left(6{x}^{2}+5x-6\right)+4B{x}^{2}+6Bx+6C{x}^{2}-4Cx
Agrupamos.
x+1={x}^{2}\left(6A+4B+6C\right)+x\left(5A+6B-4C\right)-6A
Igualamos.
\begin{array}{c}6A+4B+6C=0\\ 5A+6B-4C=1\\ -6A=1\end{array}
Obtenemos el valor de A inmediatamente.
A=-\frac{1}{6}
Sustituimos en las otras dos ecuaciones.
\begin{array}{c}6\left(-\frac{1}{6}\right)+4B+6C=0\\ 5\left(-\frac{1}{6}\right)+6B-4C=1\end{array}\to \begin{array}{c}-1+4B+6C=0\\ -\frac{5}{6}+6B-4C=1\end{array}
\begin{array}{c}4B+6C=1\\ 36B-24C=11\end{array}
No vamos a detallar los pasos para la solución del SEL, pero ya sabes que puedes aplicar cualquiera de los métodos que conozcas. En este caso, conviene más aplicar reducción. Los valores de B y C son: B=\frac{15}{52} y C=-\frac{1}{39} . Sustituyendo en las fracciones parciales.
\frac{-\frac{1}{6}}{2x}+\frac{\frac{15}{52}}{3x-2}+\frac{-\frac{1}{39}}{2x+3}=-\frac{1}{12x}+\frac{15}{52\left(3x-2\right)}-\frac{1}{39\left(2x+3\right)}
Finalmente:
\frac{{x}^{2}-1}{2x\left(3x-2\right)\left(x-1\right)\left(2x+3\right)}=-\frac{1}{12x}+\frac{15}{52\left(3x-2\right)}-\frac{1}{39\left(2x+3\right)}
Comparando con las opciones, concluimos que la respuesta correcta se encuentra en a).
Reactivo 37
¿Cuál es el resultado de aplicar fracciones parciales al integrando de la siguiente integral indefinida?
\int \frac{4-x}{\left(x+1\right)\left({x}^{2}+1\right)}dx
- \int \frac{1}{x+1}dx+\int \frac{5x-3}{2\left({x}^{2}+1\right)}dx
- \int \frac{5}{2\left(x-1\right)}dx+\int \frac{-5x+3}{2\left({x}^{2}-1\right)}dx
- \int \frac{5}{2\left(x+1\right)}dx+\int \frac{-5x+3}{2\left({x}^{2}+1\right)}dx
- \int \frac{1}{x+1}dx+\int \frac{x+3}{2\left({x}^{2}+1\right)}dx
Solución:
En este caso, no debemos resolver la integral, solo separar el integrando en fracciones parciales, por esta razón solo nos concentramos en dicho elemento. Comenzamos por inspeccionar la fracción en búsqueda de alguna simplificación, pero tanto los factores en el numerador como en el denominador son primos.
\frac{4-x}{\left(x+1\right)\left({x}^{2}+1\right)}=\frac{A}{x+1}+\frac{Bx+C}{{x}^{2}+1}
Procedemos a pasar multiplicando el denominador de la izquierda.
4-x=A\left({x}^{2}+1\right)+\left(Bx+C\right)\left(x+1\right)
Desarrollamos y agrupamos.
{x}^{2}\left(A+B\right)+x\left(B+C\right)+A+C=-x+4
Igualamos.
\begin{array}{c}A+B=0\\ B+C=-1\\ A+C=4\end{array}
Podemos aplicar cualquier método para resolver SEL, en este caso puede ser más útil el método por reducción. Omitiremos el proceso, para no desviar demasiado el propósito del ejercicio. Los valores son:
A=\frac{5}{2}, B=-\frac{5}{2}, C=\frac{3}{2}
Sustituimos en la fracción original y simplificamos.
\frac{\frac{5}{2}}{x+1}+\frac{-\frac{5}{2}x+\frac{3}{2}}{{x}^{2}+1}=\frac{5}{2\left(x+1\right)}+\frac{-5x+3}{2\left({x}^{2}+1\right)}
Sustituimos en la integral.
\int \frac{4-x}{\left(x+1\right)\left({x}^{2}+1\right)}dx=\int \frac{5}{2\left(x+1\right)}dx+\int \frac{-5x+3}{2\left({x}^{2}+1\right)}dx
Comparando el resultado con las opciones, concluimos que la respuesta correcta se encuentra en la c).
Reactivo 38
Dada la función g\left(x\right)={x}^{2}+1 , ¿cuál de las siguientes opciones permite calcular su derivada por definición?
- \underset{\mathrm{\Delta }h\to 0}{\mathrm{lim}}\frac{{\left(x+\mathrm{\Delta }h\right)}^{2}+1-{x}^{2}-1}{\mathrm{\Delta }h+x}
- \underset{\mathrm{\Delta }h\to 0}{\mathrm{lim}}\frac{{\left(x+\mathrm{\Delta }h\right)}^{2}+1-{x}^{2}-1}{\mathrm{\Delta }h}
- \underset{\mathrm{\Delta }h\to 0}{\mathrm{lim}}\frac{{\mathrm{\Delta }h}^{2}+1-{x}^{2}-1}{x}
- \underset{\mathrm{\Delta }h\to 0}{\mathrm{lim}}\frac{{\mathrm{\Delta }h}^{2}+1-{x}^{2}-1}{\mathrm{\Delta }h}
Solución:
Recordemos la definición de la derivada de una función:
\underset{\mathrm{\Delta }h\to 0}{\mathrm{lim}}\frac{f\left(x+\mathrm{\Delta }h\right)-f\left(x\right)}{\mathrm{\Delta }h}
Por tanto, debemos encontrar a f\left(x+\mathrm{\Delta }h\right) sustituyendo en los lugares con x a x+\mathrm{\Delta }h .
f\left(x+\mathrm{\Delta }h\right)={\left(x+\mathrm{\Delta }h\right)}^{2}+1
Sustituimos en el límite.
\underset{\mathrm{\Delta }h\to 0}{\mathrm{lim}}\frac{{\left(x+\mathrm{\Delta }h\right)}^{2}+1-{x}^{2}-1}{\mathrm{\Delta }h}
Este límite nos permitiría calcular la derivada de la función.
Comparando con las opciones, la respuesta correcta se encuentra en el inciso b).
Reactivo 39
Calcule la segunda derivada de y={e}^{\mathrm{cos}x} es:
- {e}^{\mathrm{cos}\left(x\right)}{\mathrm{sin}}^{2}\left(x\right)-{e}^{\mathrm{cos}\left(x\right)}\mathrm{cos}\left(x\right)
- {e}^{\mathrm{cos}\left(x\right)}{\mathrm{sin}}^{2}\left(x\right)+{e}^{\mathrm{cos}\left(x\right)}\mathrm{cos}\left(x\right)
- {e}^{\mathrm{cos}\left(x\right)}\mathrm{sin}\left(x\right)+{e}^{\mathrm{cos}\left(x\right)}\mathrm{cos}\left(x\right)
- {e}^{\mathrm{cos}\left(x\right)}\mathrm{sin}\left(x\right)-{e}^{\mathrm{cos}\left(x\right)}{\mathrm{cos}}^{2}\left(x\right)
Solución:
Calcular la segunda derivada de una función real, consiste en derivar dos veces de forma consecutiva. Comenzamos aplicando la fórmula de la derivada de {e}^{f\left(x\right)} .
{y}^{\text{'}}={\left({e}^{\mathrm{cos}x}\right)}^{\text{'}}={\left(\mathrm{cos}x\right)}^{\text{'}}\cdot {e}^{\mathrm{cos}x}=-\mathrm{sin}x\cdot {e}^{\mathrm{cos}x}
Derivamos nuevamente, en este caso, debemos iniciar aplicando la derivada de un producto.
{y}^{\text{'}\text{'}}={\left(-\mathrm{sin}x\cdot {e}^{\mathrm{cos}x}\right)}^{\text{'}}=-\mathrm{sin}x\cdot {\left({e}^{\mathrm{cos}x}\right)}^{\text{'}}-{\left(\mathrm{sin}x\right)}^{\text{'}}\cdot {e}^{\mathrm{cos}x}
Resolvemos.
{y}^{\text{'}\text{'}}={\mathrm{sin}}^{2}x\cdot {e}^{\mathrm{cos}x}-\mathrm{cos}x\cdot {e}^{\mathrm{cos}x}
Comparando con las opciones, concluimos que la respuesta correcta se encuentra en a).
Reactivo 40
La derivada de y=\mathrm{ln}\left({x}^{2}+1\right) es:
- {y}^{\text{'}}=-\frac{x}{{x}^{2}+1}
- {y}^{\text{'}}=-\frac{2x}{{x}^{2}+1}
- {y}^{\text{'}}=\frac{2x}{{x}^{2}-1}
- {y}^{\text{'}}=\frac{2x}{{x}^{2}+1}
Solución:
Calcular la derivada de esta función será bastante sencillo. Iniciamos aplicando la fórmula de la derivada del logaritmo.
{y}^{\text{'}}={\left[\mathrm{ln}\left({x}^{2}+1\right)\right]}^{\text{'}}=\frac{{\left({x}^{2}+1\right)}^{\text{'}}}{{x}^{2}+1}
Resolvemos la derivada indicada aplicando la derivada de la suma.
{y}^{\text{'}}=\frac{2x}{{x}^{2}+1}
Comparando con las opciones, escogemos a la d) como la correcta.

