Examen Simulador IPN Matemáticas CMB P.3 – Reactivos 21 al 30

Tercera entrega del examen simulacro de matemáticas del IPN para las carreras del área de ciencias médico biológicas, vamos a resolver los reactivos del 21 al 30.

Reactivo 21: diferencial de una función

Calcule el diferencial de la función f\left(x\right)=\frac{1}{{x}^{2}+1} .

1. -\frac{2x}{{\left({x}^{2}+1\right)}^{2}}dx
2. \frac{2x}{{\left({x}^{2}+1\right)}^{2}}dx
3. -\frac{x}{{\left({x}^{2}+1\right)}^{2}}dx
4. -\frac{2x}{{x}^{2}+1}dx

Solución:

Para calcular el diferencial df de una función cualquiera, debemos multiplicar la derivada de la función respecto a x por el diferencial de x .

dy={f}^{\text{'}}\left(x\right)dx

Por tanto, comenzamos calculando la derivada de f .

{f}^{\text{'}}\left(x\right)={\left[\frac{1}{{x}^{2}+1}\right]}^{\text{'}}=\frac{{\left(1\right)}^{\text{'}}\left({x}^{2}+1\right)-{\left({x}^{2}+1\right)}^{\text{'}}}{{\left({x}^{2}+1\right)}^{2}}

Resolvemos.

{f}^{\text{'}}\left(x\right)=-\frac{2x}{{\left({x}^{2}+1\right)}^{2}}

Finalmente, multiplicamos la derivada por el diferencial de x , es decir dx .

dy=-\frac{2x}{{\left({x}^{2}+1\right)}^{2}}dx

Comparando con las opciones, concluimos que la respuesta correcta es el inciso a).

Reactivo 22: derivada de una función

Si la derivada de una función f\left(x\right) es igual a cero \frac{df}{dx}=0 , significa que f …

1. Es una función real
2. No es derivable
3. Es constante
4. Tiende a cero en infinito

Solución:

Responder esta pregunta es relativamente sencillo si tenemos presente las propiedades de la derivada de una constante.

\frac{d\left(c\right)}{dx}=0

Pero, ¿por qué es cero la derivada de una constante? Esta pregunta podemos resolverla si recurrimos a la definición de derivada.

\underset{h\to 0}{\mathrm{lim}}\frac{f\left(x+h\right)-f\left(x\right)}{h}

Si f\left(x\right)=c , una función constante, nos daremos cuenta que no hay ninguna x en la que podamos sustituir x+h , por tanto:

\underset{h\to 0}{\mathrm{lim}}\frac{c-c}{h}=0

Desde el punto de vista analítico, podemos concluir que la derivada de una función es cero cuando la misma no presenta cambio en determinado intervalo, dicho de otra forma, permanece constante.

Concluimos indicando como respuesta correcta la opción c).

Reactivo 23: límite de una función

Encuentre el valor del siguiente límite.

\underset{x\to \infty }{\mathrm{lim}}4\left({e}^{1-{x}^{2}}+1\right)

1. \infty
2. -\infty
3. 0
4. 4

Solución:

Antes de continuar aplicando cualquier método para resolver límites, es necesario que evaluemos a la función en el punto al que tiende x , para identificar la existencia de alguna indeterminación.

\underset{x\to \infty }{\mathrm{lim}}4\left({e}^{1-{x}^{2}}+1\right)=4\left({e}^{1-{\infty }^{2}}+1\right)=4\left({e}^{1-\infty }+1\right)=4\left({e}^{-\infty }+1\right)

El término {e}^{-\infty } puede escribirse como \frac{1}{{e}^{\infty }} , cantidad que es igual a cero.

=4\left(0+1\right)=4

Concluimos entonces:

\underset{x\to \infty }{\mathrm{lim}}4\left({e}^{1-{x}^{2}}+1\right)=4

Comparando con las opciones, la respuesta correcta se encuentra en el inciso d).

Reactivo 24: inecuaciones

Resuelva la siguiente desigualdad.

x+1-\frac{x-1}{3}>2x+1

1. x>\frac{1}{4}
2. x<\frac{1}{4}
3. x<-\frac{1}{4}
4. x>-\frac{1}{4}

Solución:

Para resolver cualquier inecuación, solo debemos tener presente las reglas de las desigualdades, principalmente que multiplicar o dividir por un número negativo hará que la desigualdad cambie de sentido. Comencemos por multiplicar todo por 3.

3x+3-x+1>6x+3

Ahora, agrupamos los términos con x a la izquierda y los independientes a la derecha.

3x-x-6x>3-3-1

Resolvemos las sumas y restas correspondientes.

-4x>-1

Dividimos ambos miembros por -4 y cambiamos el sentido de la desigualdad.

x<\frac{1}{4}

Comparando con las opciones, la respuesta correcta se encuentra en el inciso b).

Reactivo 25: derivada de una función

Obtenga la derivada de la siguiente función.

y=\frac{{x}^{2}}{1-x}

1. \frac{1}{{\left(1-x\right)}^{2}}
2. \frac{1-2x}{{\left(1-x\right)}^{2}}
3. \frac{2x-1}{{\left(1-x\right)}^{2}}
4. \frac{2x-{x}^{2}}{{\left(1-x\right)}^{2}}

Solución:

En este caso, debemos identificar qué propiedades y técnicas de derivación serán útiles para encontrar a {y}^{\text{'}} . Inspeccionando la función, nos damos cuenta que se trata de una fracción, por tanto, aplicamos la fórmula para la derivada de un cociente.

{y}^{\text{'}}=\frac{{\left({x}^{2}\right)}^{\text{'}}\left(1-x\right)-{\left(1-x\right)}^{\text{'}}\left({x}^{2}\right)}{{\left(1-x\right)}^{2}}

Resolvemos las derivadas indicadas.

\frac{{\left({x}^{2}\right)}^{\text{'}}\left(1-x\right)-{\left(1-x\right)}^{\text{'}}\left({x}^{2}\right)}{{\left(1-x\right)}^{2}}=\frac{2x\left(1-x\right)-\left(-1\right)\left({x}^{2}\right)}{{\left(1-x\right)}^{2}}

Simplificamos la expresión.

\frac{2x-2{x}^{2}+{x}^{2}}{{\left(1-x\right)}^{2}}=\frac{2x-{x}^{2}}{{\left(1-x\right)}^{2}}

Comparando con las opciones, la respuesta correcta es el inciso d).

Reactivo 26: coordenadas polares

Encuentre la expresión de la parábola y={x}^{2}-x+2 en coordenadas polares.

1. {r}^{2}{\mathrm{cos}}^{2}\theta +r\left(\mathrm{sin}\theta +\mathrm{cos}\theta \right)+2=0
2. {r}^{2}{\mathrm{cos}}^{2}\theta -r\left(\mathrm{sin}\theta -\mathrm{cos}\theta \right)+2=0
3. {r}^{2}{\mathrm{cos}}^{2}\theta -r\left(\mathrm{sin}\theta +\mathrm{cos}\theta \right)+2=0
4. {r}^{2}{\mathrm{cos}}^{2}\theta +r\left(\mathrm{sin}\theta +\mathrm{cos}\theta \right)-2=0

Solución:

Para realizar una conversión a coordenadas polares de cualquier expresión en coordenadas rectangulares, debemos tener presente las siguientes igualdades:

x=r\mathrm{cos}\theta 

y=r\mathrm{sin}\theta 

Estas igualdades se obtienen al descomponer el vector de magnitud r y ángulo \theta  en el plano cartesiano. Procedemos a sustituir x y y por las identidades anteriores.

r\mathrm{sin}\theta ={r}^{2}{\mathrm{cos}}^{2}\theta -r\mathrm{cos}\theta +2

Pasamos todo a un mismo miembro.

{r}^{2}{\mathrm{cos}}^{2}\theta -r\mathrm{cos}\theta +2-r\mathrm{sin}\theta =0

Acomodamos la expresión.

{r}^{2}{\mathrm{cos}}^{2}\theta -r\left(\mathrm{sin}\theta +\mathrm{cos}\theta \right)+2=0

Comparando con las opciones, queda claro que la respuesta correcta se encuentra en el inciso c).

Reactivo 27: foco de la parábola

Determine las coordenadas del foco de la parábola y=2{x}^{2}+3x-5 .

1. f\left(-3, 6\right)
2. f\left(-\frac{3}{4}, -6\right)
3. f\left(\frac{3}{4},-6\right)
4. f\left(\frac{3}{4}, 6\right)

Solución:

Para encontrar el foco de cualquier parábola, primero debemos identificar si es una parábola con eje focal sobre las abscisas o sobre las ordenadas. En este caso, debido a que es la x quién está elevada al cuadrado, la parábola tiene el eje focal paralelo a las ordenadas.

Las coordenadas del foco son:

f\left(h, k+p\right)

Para encontrar las coordenadas del vértice y el lado recto p , debemos completar cuadrados.

\frac{y}{2}={x}^{2}+\frac{3}{2}x-\frac{5}{2}

Pasamos a sumar \frac{5}{2} .

\frac{y}{2}+\frac{5}{2}={x}^{2}+\frac{3}{2}x

Por el producto notable del cuadrado de un binomio sabemos que:

2ab=\frac{3}{2}x\to a=x, b=\frac{3}{4}

Por tanto, debemos sumar en ambos miembros el cuadrado de \frac{3}{4} .

\frac{y}{2}+\frac{5}{2}+\frac{9}{16}={x}^{2}+\frac{3}{2}x+\frac{9}{16}

Aplicando {\left(x+a\right)}^{2} en sentido contrario nos queda:

\frac{y}{2}+\frac{49}{16}={\left(x+\frac{3}{4}\right)}^{2}

Extraemos factor común \frac{1}{2} .

\frac{1}{2}\left(y+\frac{49}{8}\right)={\left(x+\frac{3}{4}\right)}^{2}

Las coordenadas del vértice son:

V\left(-\frac{3}{4}, -\frac{49}{8}\right)

Mientras que el lado recto es:

4p=\frac{1}{2}\to p=\frac{1}{8}

Finalmente:

f\left(-\frac{3}{4},\frac{1}{8}-\frac{49}{8}\right)=f\left(-\frac{3}{4},-6\right)

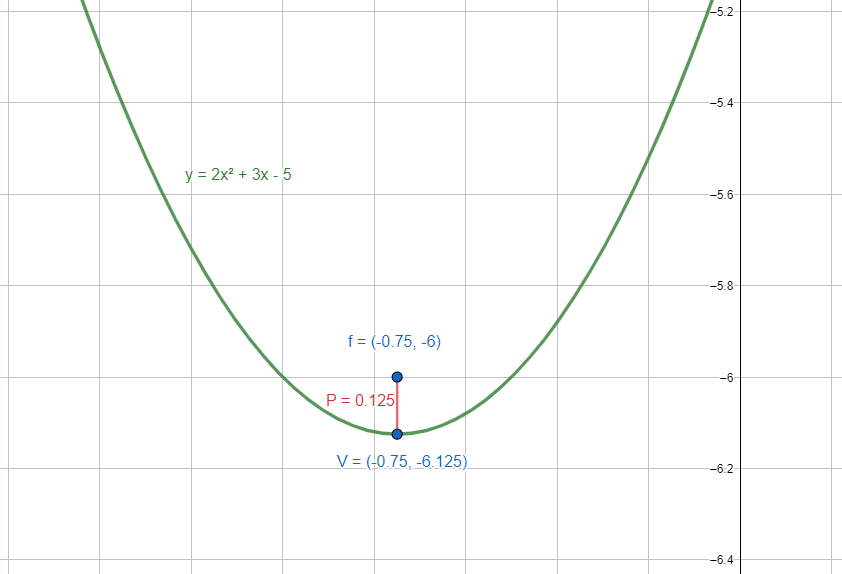
Comparando con las opciones, concluimos que la respuesta correcta se encuentra en el inciso b).

Reactivo 28: punto medio

Determine el punto medio del segmento que tiene por extremos a los puntos A\left(1, 1\right) y B\left(-3, 5\right) .

1. \left(1, 3\right)
2. \left(1, -3\right)
3. \left(-1, -3\right)
4. \left(-1, 3\right)

Solución:

Para calcular el punto medio de un segmento dados sus extremos, utilizamos la siguiente ecuación:

M\left(\frac{{x}_{1}+{x}_{2}}{2},\frac{{y}_{1}+{y}_{2}}{2}\right)

Sustituimos las coordenadas de los puntos A y B en la ecuación.

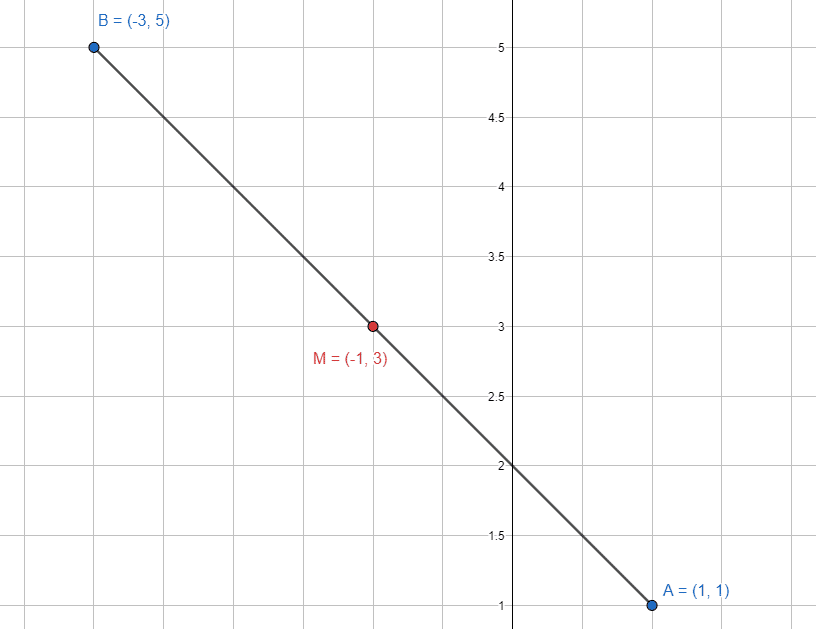
M\left(\frac{1-3}{2},\frac{1+5}{2}\right)=M\left(-1, 3\right)

Gráficamente, la solución se vería como muestra la figura.

Comparando con las opciones, la respuesta correcta se encuentra en el inciso d).

Reactivo 29: elementos de la elipse

Se llama _________ de una elipse, es la razón entre la longitud entre el centro y uno de sus focos c , y el semieje mayor a .

1. Pendiente
2. Tangente
3. Excentricidad
4. Eje focal

Solución:

Las secciones cónicas son objetos de la geometría analítica que pueden describirse a partir de un determinado conjunto de parámetros, de tal forma que dichas cantidades puedan cuantificar todas sus propiedades.

En el caso de la elipse, existe un parámetro denominado excentricidad el cual se calcula como la razón entre el centro y uno de sus focos y el semieje mayor.

e=\frac{c}{a}

Teniendo en cuenta esta definición, podemos completar la frase del enunciado con el término del inciso c):

Se llama excentricidad de una elipse, es la razón entre la longitud entre el centro y uno de sus focos c , y el semieje mayor a .

Reactivo 30: lugar geométrico

¿Cuál de las siguientes frases describe con palabras el lugar geométrico de una circunferencia?

1. Es el conjunto de puntos que distan igual de un punto móvil llamado centro
2. Es el conjunto de puntos que equidistan igual de dos puntos fijos en el plano
3. Es el conjunto de puntos cuya distancia a otros dos fijos varía linealmente
4. Es el conjunto de puntos que distan igual de un punto fijo llamado centro

Solución:

Para responder esta pregunta, simplemente debemos recordar la ecuación general de una circunferencia:

{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}

Si aplicamos raíz cuadrada en ambos lados nos queda:

r=\sqrt{{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}}

Esta ecuación no es más que una forma generalizada de medir la distancia entre dos puntos. La gran diferencia es que esa distancia ya se encuentra establecida y su valor es r , por tanto, nos interesan los valores de x y y que distan r del centro h, k .

Teniendo en cuenta lo anterior podemos concluir que:

La circunferencia es el lugar geométrico en el plano cuyos puntos x y y distan una longitud constante r de un punto fijo llamado centro h, k .

Concluimos entonces que la respuesta correcta se encuentra en el inciso d).