Hola de nuevo aspirante, vamos a continuar con los reactivos del 11 al 20 del examen simulador de matemáticas para el examen de admisión al IPN en el área de ciencias médico biológicas.

Recuerda hacer apuntes y medir tu tiempo, lo ideal es que simules la aplicación del examen real.
Reactivo 11: valor de la función
Obtenga el valor de evaluar la función f\left(x\right)=\mathrm{ln}\left({x}^{2}-3\right) , cuando x=-2 .
- \mathrm{ln}\left(0\right)
- 0
- \infty
- No existe
Solución:
Para evaluar funciones en un punto dado, simplemente debemos sustituir a la variable independiente, en este caso x , por el número real indicado, es decir, x=-2 . Luego, desarrollamos las operaciones que hagan falta.
Reemplazamos:
f\left(-2\right)=\mathrm{ln}\left({\left(-2\right)}^{2}-3\right)
Resolvemos la potencia y luego la diferencia en el argumento del logaritmo.
f\left(-2\right)=\mathrm{ln}\left(4-3\right)=\mathrm{ln}\left(1\right)
Por definición, sabemos que el logaritmo para cualquier base de 1 es cero, por tanto:
f\left(-2\right)=0
Comparando con las opciones, concluimos que la respuesta correcta es el inciso b).
Reactivo 12: identidad trigonométrica
Identificar cuál es la identidad trigonométrica para el coseno de la suma de ángulos.
- \mathrm{cos}\left(x+y\right)=\mathrm{cos}\left(x\right)\mathrm{cos}\left(y\right)-\mathrm{sin}\left(x\right)\mathrm{sin}\left(y\right)
- \mathrm{cos}\left(x+y\right)=\mathrm{cos}\left(x\right)\mathrm{cos}\left(y\right)+\mathrm{sin}\left(x\right)\mathrm{sin}\left(y\right)
- \mathrm{cos}\left(x+y\right)=\mathrm{cos}\left(x\right)\mathrm{sin}\left(y\right)-\mathrm{sin}\left(x\right)\mathrm{cos}\left(y\right)
- \mathrm{cos}\left(x+y\right)=\mathrm{cos}\left(x\right)\mathrm{sin}\left(y\right)+\mathrm{sin}\left(x\right)\mathrm{cos}\left(y\right)
Solución:
Para encontrar la respuesta correcta a este ejercicio, es necesario que previamente hayas estudiado las identidades trigonométricas básicas y sus aplicaciones. La razón de esto, es porque demostrar en un examen el coseno de la suma de dos ángulos puede jugarte en contra, teniendo en cuenta que tomará mucho tiempo y gastarás energía en algo que puedes memorizar.
En esta ocasión no la vamos a demostrar, porque excede las intenciones de este simulacro resuelto. Teniendo en cuenta las tablas de identidades trigonométricas elementales y examinando las opciones, concluimos que la respuesta correcta se encuentra en el inciso a).
Reactivo 13: posición entre rectas
Dadas dos rectas en el plano, éstas son ____________ entre sí cuando sus pendientes cumplen la siguiente propiedad: {m}_{1}=-\frac{1}{{m}_{2}} .
- Paralelas
- Iguales
- Perpendiculares
- Coplanares
Solución:
La fórmula que se indica en el enunciado, corresponde a la relación que tienen que cumplir las pendientes de dos rectas para que éstas sean perpendiculares entre sí. Teniendo en cuenta esto y examinando los incisos, concluimos que la frase se completa con la opción c).
Dadas dos rectas en el plano, éstas son perpendiculares entre sí cuando sus pendientes cumplen la siguiente propiedad: {m}_{1}=-\frac{1}{{m}_{2}} .
Reactivo 14: elementos del triángulo
El punto por el que pasan las medianas de un triángulo recibe el nombre de…
- Incentro
- Centro
- Baricentro
- Ortocentro
Solución:
Para responder correctamente al enunciado, debemos recordar los principales elementos relacionados con los triángulos, específicamente: los puntos notables y las rectas notables.
- Las mediatrices son segmentos de recta perpendiculares a cada lado del triángulo y que pasan por su punto medio. El punto de intersección de las mediatrices es el circuncentro
- Las bisectrices son segmentos de recta que dividen a la mitad los ángulos internos del triángulo. Su punto de intersección es el incentro
- Las medianas son segmentos de recta trazados desde uno de los vértices hasta el punto medio de la arista opuesta. La intersección de las medianas es el baricentro
Teniendo en cuenta lo anterior, concluimos que la respuesta correcta se encuentra en el inciso c).
Reactivo 15: ecuaciones lineales
Calcule el o los valores de x que satisface la siguiente ecuación.
{4}^{\frac{x-1}{x+1}}={16}^{x-1}
- x=1
- x=1, x=\frac{1}{2}
- x=-1, x=-\frac{1}{2}
- x=1, x=-\frac{1}{2}
Solución:
Para resolver ecuaciones con incógnitas en los exponentes, debemos trabajar las bases para que sean iguales, de tal forma que podamos igualar los exponentes para que se cumpla la igualdad. Comenzamos expresando al 16 como una potencia de base 4.
{4}^{\frac{x-1}{x+1}}={\left({4}^{2}\right)}^{x-1}
Aplicamos potencia de una potencia.
{4}^{\frac{x-1}{x+1}}={4}^{2\left(x-1\right)}
Con las bases iguales, solo nos queda igualar los exponentes.
\frac{x-1}{x+1}=2\left(x-1\right)
Multiplicamos ambos miembros por x+1 .
x-1=2\left(x-1\right)\left(x+1\right)
Desarrollamos.
x-1=2\left({x}^{2}-1\right)
x-1=2{x}^{2}-2
2{x}^{2}-x-1=0
Aplicamos la fórmula de segundo grado para encontrar las raíces:
{x}_{1}=1, {x}_{2}=-0.5
Comprobamos que estos resultados satisfagan la igualdad.
x=1\to {4}^{\frac{1-1}{1+1}}={4}^{2\left(1-1\right)}\to 1=1
x=-0.5\to {4}^{\frac{-0.5-1}{-0.5+1}}={4}^{2\left(-0.5-1\right)}\to \frac{1}{64}=\frac{1}{64}
Comprobados los resultados, solo nos queda indicar como respuesta correcta a la opción d).
Reactivo 16: valor del dinero en el tiempo
La ecuación S= ___________ representa el valor de una inversión P a la que se suman intereses simples i durante n períodos.
- P\left(1+ni\right)
- niP
- P\left(1+n+i\right)
- P{\left(1+i\right)}^{n}
Solución:
Para resolver este problema, debemos recordar la definición de interés simple: son intereses (costo de capital) que se aplica de forma constante a un capital inicial, a medida que transcurren los períodos de la deuda. Esto puede escribirse como:
S=P+iP+iP+\dots iP
Ya que hay tantos intereses o iP como n períodos, la fórmula puede escribirse como:
S=P+niP=P\left(1+ni\right)
Concluimos indicando como respuesta correcta la opción a).
Reactivo 17: valor de la función
Una compañía ha estado estudiando un modelo matemático que le permita a sus analistas obtener un modelo matemático de las ventas, dicha ecuación es V=1.26{x}^{1.5}+50 , donde x se mide en años y V en millones de ventas. ¿Cuántas ventas concretadas tendría la empresa para el año 4?
- 70 millones
- 65 millones
- 60 millones
- 55 millones
Solución:
Haciendo a un lado el enunciado y teniendo en cuenta los datos importantes como que el modelo de ventas es V\left(x\right)=1.26{x}^{1.5}+50 y que se desea conocer el número de ventas para x=4 años, este problema se resume en sustituir el valor de x en la función V\left(x\right) .
V\left(4\right)=1.26\cdot {\left(4\right)}^{1.5}+50
Resolviendo la potencia, que podemos reescribir como \sqrt{{4}^{3}} , obtenemos que:
V\left(4\right)=60 \mathrm{m}\mathrm{i}\mathrm{l}\mathrm{l}
Para el año 4, la empresa habrá concretado 60 millones de ventas.
Comparando con los incisos, la respuesta correcta se encuentra en el c).
Reactivo 18: ecuaciones lineales
Resuelva la siguiente igualdad y encuentre el valor de x .
2x-\frac{1}{3}=\frac{x}{2}+\frac{2}{3}
- -\frac{2}{3}
- \frac{1}{3}
- \frac{2}{3}
- -\frac{1}{3}
Solución:
En este caso, debemos encontrar el valor de x que satisface a la ecuación. Para resolverla, debemos seguir las reglas de las igualdades, agrupando en un miembro los términos con x y en el otro los términos independientes. Comenzamos por agrupar en el primer miembro los términos con x .
2x-\frac{x}{2}-\frac{1}{3}=\frac{2}{3}
Pasamos el \frac{1}{3} al segundo miembro.
2x-\frac{x}{2}=\frac{2}{3}+\frac{1}{3}
Resolvemos las sumas y resta de fracciones.
\frac{3}{2}x=1
Despejamos.
x=\frac{2}{3}
Concluimos indicando como respuesta correcta la opción c).
Reactivo 19: sistema de ecuaciones
Encuentre los valores de x y y que satisfacen el sistema de ecuaciones.
\left\{\begin{array}{c}x+y=5\\ 2x-5y=6\end{array}\right.
- x=\frac{31}{7},y=\frac{4}{7}
- x=-\frac{31}{7},y=\frac{4}{7}
- x=\frac{31}{7},y=-\frac{4}{7}
- x=0,y=\frac{4}{7}
Solución:
El ejercicio nos pide resolver un sistema de dos ecuaciones con dos incógnitas. Podemos utilizar cualquiera de los métodos clásicos: igualación, sustitución y reducción, o también un método basado en matrices como lo es Gauss Jordan.
Debido a la simplicidad del SEL, vamos a aplicar reducción. Comencemos por multiplicar por 5 a la primera ecuación para luego sumarla con la segunda.
5I+II:
\frac{\begin{array}{c}5x+5y=25\\ 2x-5y=6\end{array}}{7x=11}
Despejamos y obtenemos el valor de x .
x=\frac{31}{7}
Ahora, sustituimos este resultado en cualquiera de las ecuaciones para despejar a y .
I\left(x=\frac{31}{7}\right):\frac{31}{7}+y=5
Despejamos.
y=\frac{4}{7}
La solución al SEL es:
x=\frac{31}{7}, y=\frac{4}{7}
Comparando con los incisos, la respuesta correcta se encuentra en el a).
Reactivo 20: división de polinomios
Obtenga el resultado de la siguiente división de polinomios.
\frac{{x}^{3}+2{x}^{2}+x-1}{x+1}
- {x}^{2}+x+\frac{1}{x+1}
- {x}^{2}+x-\frac{1}{x+1}
- {x}^{2}+x
- x-\frac{1}{x+1}
Solución:
En este caso, debemos aplicar el algoritmo de la división sintética para encontrar la división indicada por el enunciado. Recordemos que debemos ir eliminando uno a uno los términos de mayor grado en el polinomio hasta que el grado del dividendo sea menor al grado del divisor.
Reescribimos la división como se muestra a continuación.
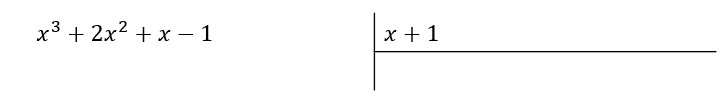
El primer monomio será {x}^{2} que multiplicado por x+1 nos permitirá eliminar a {x}^{3} en el dividendo.
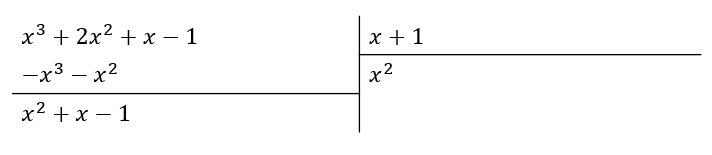
Recordemos que el resultado de multiplicar {x}^{2} con x+1 se debe escribir con signo contrario. Continuamos con x para eliminar a {x}^{2} .
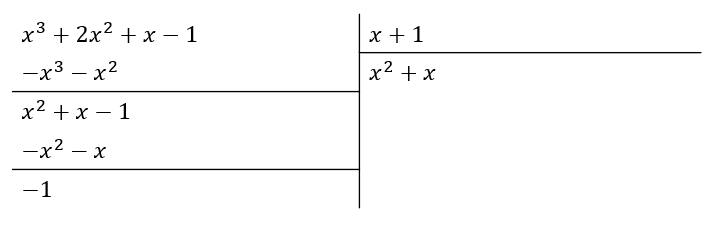
Llegados a este punto, el grado del dividendo es menor que el grado del divisor. Concluimos entonces que:
\frac{{x}^{3}+2{x}^{2}+x-1}{x+1}={x}^{2}+x-\frac{1}{x+1}
Comparando con las opciones, la respuesta correcta se encuentra en el inciso b).


