Guía UDG resuelta PAA | Matemáticas reactivos del 1 al 10

Hola aspirante, en este tutorial vamos a resolver los primeros 10 reactivos de la guía del examen de admisión a la UDG. Recuerda que el examen que vas a presentar la prueba de aptitud académica de College Board.

Parte II

Si tienes dudas sobre el proceso de admisión aquí tienes un resumen:

Vamos a dividir la solución de la guía en 5 partes, para acceder a los siguientes 10 reactivos simplemente dale clic en siguiente.

Estructura del examen de la UDG

Como te comente hace un momento el examen de ingreso a la UDG consta de 4 áreas de estudio, si bien este tutorial solo abarcara la parte correspondiente al área de matemáticas es importante que estudies todas las áreas del examen.

Te dejo la estructura del examen para que conozcas las áreas que tienes que estudiar:

• Lectura (45 reactivos).
• Redacción (25 reactivos).
• Matemáticas (55 reactivos).
• Inglés (50 reactivos).

La parte de inglés no cuenta en el examen de ingreso a la UDG. Recuerda que el organismo encargado de realizar este examen es el College Board.

Guía UDG resuelta

Antes de consultar la guía de la UDG resuelta en la parte de matemáticas, te recomiendo que intentes solucionar los ejercicios por tu propia cuenta, de esa forma podrás medir tu nivel de conocimientos.

Otro punto importante es que no te quedes únicamente con los ejercicios resueltos, si bien la guía es una buena forma de estudiar, es necesario profundizar en cada uno de los temas de matemáticas por separado para obtener un buen puntaje en el examen de admisión a la universidad de Guadalajara.

Una vez que identifiques los temas que más se te dificultan, comienza a estudiarlos y a realizar ejercicios, recuerda que la mejor forma de obtener un buen puntaje es dominar los temas, y sobre todo practicar.

Reactivo 1: La recta real

En la figura anterior, ¿cuál es el número que está representado por el punto A ?

1. \frac{1}{2}
2. 2
3. 2-\frac{3}{4}
4. \frac{3}{2}

Solución:

En la figura del problema, podemos observar un eje real y en él, un punto entre 1 y 2. Por simple inspección, nos daremos cuenta que dicho punto se encuentra en la mitad de 1 y 2, es decir media unidad por encima de 1 o media unidad por debajo de 2.

Podemos representar a ese punto de dos formas: sumándole media unidad a 1 o restándole media unidad a 2, en este caso se hará de la primera. Recordemos que media unidad es 0.5 o \frac{1}{2} .

A=1+\frac{1}{2}

Resolvemos la suma de fracciones.

A=\frac{2+1}{2}=\frac{3}{2}

Concluimos indicando que: el número que representa al punto A es \frac{3}{2} . Comparando con las opciones, seleccionamos como correcta a la D.

Reactivo 2: Proporciones y porcentajes

Un boleto de lotería costó $10 y fue premiado con $27,000. Al pagar el boleto, Juan aportó $2, Andrés $3 y Pedro $5. El premio se dividió proporcionalmente a lo aportado. ¿Cuánto recibió Pedro?

1. $18,000
2. $13,500
3. $8,100
4. $5,400

Solución:

El problema nos dice que el premio de un boleto de lotería se va a repartir entre 3 personas en base al mismo porcentaje que cada uno haya invertido en la compra del boleto.

Es decir, para determinar cuánto del premio le tocó a Pedro, debemos calcular el porcentaje que aportó él para la compra del boleto; ese mismo será su porcentaje de ganancia.

Dividimos el aporte en pesos sobre el costo total del boleto por cien.

\%P=\frac{\$5}{\$10}*100\%=50\%

Pedro pagó el 50% del costo del boleto, por tanto le toca un 50% del premio, es decir la mitad.

Premio para Pedro=\frac{\$\mathrm{27,000}}{2}=\$\mathrm{13,500}

Pedro ha ganado $13,500 del boleto de lotería.

Concluimos seleccionando la opción B como la respuesta correcta.

Reactivo 3: Problemas matemáticos

Rosa distribuye la promoción de un producto B a cada segunda persona de la fila para entrar a un concierto. Pablo distribuye la promoción de un producto C en la misma fila a cada tercera persona. ¿Qué número ocupa en la fila la segunda persona que recibirá la promoción de ambos productos?

1. 5
2. 8
3. 10
4. 12

Solución:

Tenemos dos caminos posibles para resolver este problema:

• De forma gráfica, dibujando a las personas de la fila hasta identificar al primero que reciba ambas promociones
• De forma matemática, aplicando el concepto de mínimo común múltiplo

El método más rápido es el segundo: aplicar mínimo común múltiplo. Pero, ¿Por qué mínimo común múltiplo? Pensemos en el problema de la siguiente forma:

Necesitamos encontrar un punto donde los avances de 2 en 2 de Rosa y los de 3 en 3 de Pablo coincidan, es decir, el mínimo número que pueda dividirse entre 2 y 3, por esta razón aplicamos mínimo común múltiplo.

mcm\left(\mathrm{2,3}\right)=6

Ahora, 6 es la posición de la primera persona que recibe la promoción de ambos, necesitamos la segunda y para eso multiplicamos por 2.

Entonces, la segunda persona que recibe la promoción de Rosa y Pablo está en la posición:

2*6=12

Concluimos seleccionando como respuesta correcta a la opción D.

Reactivo 4: Números primos

Si p es un número primo, p>2 ¿Cuántos factores positivos tiene 4p ?

1. 3
2. 4
3. 5
4. 6

Solución:

Para obtener la cantidad de factores (o divisores) de cualquier número entero a escrito en la forma a={b}^{n}{c}^{m}{d}^{p}\dots  se calcula el siguiente producto \left(n+1\right)\left(m+1\right)\left(p+1\right) . Es decir, el número de factores (o divisores) se obtiene al multiplicar el exponente de cada factor primo sumado 1.

A 4p lo podemos escribir como {2}^{2}p , sus factores primos son 2 elevado al cuadrado y p elevado a 1, por tanto el número de factores (o divisores) positivos es:

Fp=\left(2+1\right)\left(1+1\right)=6

Comparando este resultado con las opciones del problema, seleccionamos como correcta a la D.

Reactivo 5: Algoritmo de la multiplicación

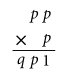
En la multiplicación anterior p y q representan dígitos diferentes a 0. ¿Cuál es el valor de q ?

1. 1
2. 2
3. 8
4. 9

Solución:

Ya que el primer producto que se realiza es p*p , es decir un número de una sola cifra multiplicado por sí mismo, debemos ubicar qué números del 1 al 9 elevados al cuadrado terminan en 1.

Los únicos que cumplen con esa condición son el 1 y el 9. El 1 no puede ser porque haría que q valiera cero, por tanto nos queda el 9.

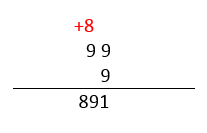
De esta forma, queda claro que p=9 y q=8 . Comparando nuestro resultado con los incisos del problema, seleccionamos como respuesta correcta al C.

Reactivo 6: Potencias y descomposición en factores

Si \mathrm{1,200}={2}^{4}\times 3\times {5}^{2} , ¿Cuál de los siguientes es un múltiplo de 1,200?

1. {2}^{5}\times {3}^{2}\times {5}^{2}
2. {2}^{2}\times {3}^{2}\times {5}^{3}
3. {2}^{3}\times {3}^{2}\times {5}^{2}
4. 2\times 3\times 5

Solución:

Recordemos que: un número a es múltiplo de otro número b si \frac{a}{b} da como resultado un número entero. Por esta razón, sabemos que alguna de las opciones es múltiplo de \mathrm{1,200}={2}^{4}\times 3\times {5}^{2} si al dividir la opción por 1,200 el resultado es un entero.

Ya que las opciones están expresadas como el producto de potencias y el enunciado nos da a 1,200 en esa forma, podemos identificar fácilmente que algún inciso es múltiplo de 1,200 si todos los exponentes para cada factor son mayores o iguales que los de \mathrm{1,200}={2}^{4}\times 3\times {5}^{2} .

El único que cumple con esta condición es el inciso A, porque el 2 tiene exponente 5 ( 5>4 ), el 3 exponente 2 ( 2>1 ) y el 5 exponente 2 ( 2=2 ). El resto tiene por lo menos un factor con exponente menor y eso rompe con la condición.

Concluimos indicando al inciso A como la respuesta correcta.

Reactivo 7: Porcentajes

Un artículo tiene un 50% de descuento de su precio original. Además, tiene un 10% de descuento adicional sobre su precio especial ¿Cuál es el porcentaje de descuento real que tiene el artículo?

1. 45
2. 53
3. 55
4. 60

Solución:

Al producto se le aplica un descuento del 50% al precio original, quedando el precio del primer descuento como:

{P}_{d1}=P\left(1-0.5\right)=0.5P

Ahora, al precio del primer descuento se le aplica un segundo descuento del 10%:

{P}_{d2}={P}_{d1}\left(1-0.1\right)=0.9{P}_{d1}

Sustituimos a {P}_{d1}=0.5P .

{P}_{d2}=0.9*0.5P=0.45P

El descuento total lo encontramos restándole al precio original el precio con todos los descuentos aplicados:

{D}_{t}=P-0.45P=0.55P

Es decir, el descuento total es del 55% respecto al precio real del producto.

Comparando con las opciones del problema, seleccionamos como respuesta correcta a la opción C.

Reactivo 8: Fracciones y proporciones

Carmen compró 5 metros de alambre y utilizar \frac{3}{4} partes. ¿Cuántos metros de alambre le sobraron?

1. \frac{1}{4}
2. 1\frac{1}{4}
3. 1\frac{3}{4}
4. 3\frac{3}{4}

Solución:

Para calcular la cantidad de metros de cable que le sobraron Carmen, debemos multiplicar el total de metros, 5 por la fracción de alambre que no utilizo, es decir \frac{1}{4} .

Metros restantes=5 m*\frac{1}{4}=\frac{5}{4} m

Ninguna de las opciones del problema parece ser \frac{5}{4} , debemos convertir nuestro resultado a fracción mixta.

\frac{5}{4} m=1\frac{1}{4} m

Ahora sí, comparando con los incisos, seleccionamos como correcta a la opción B.

Reactivo 9: Operaciones aritméticas

El valor de 2-3(5+2)(5-8) es:

1. -110
2. -61
3. 21
4. 65

Solución:

Para resolver este tipo de problemas, debemos seguir el siguiente orden con las operaciones:

1. Operaciones dentro de paréntesis
2. Multiplicaciones y divisiones
3. Sumas y restas

Resolvemos el interior de los paréntesis.

2-3\left(5+2\right)\left(5-8\right)=2-3\left(7\right)\left(-3\right)=2+3*7*3

Resolvemos los productos en el segundo término.

2+3*7*3=2+63

Ahora, la suma pendiente.

2+63=65

Concluimos finalmente que:

El valor de 2-3(5+2)(5-8) es 65.

Con base en las opciones en los incisos, escogemos como correcta a la D.

Reactivo 10: Simplificación de radicales

¿Cuál es la simplificación de la expresión \sqrt{50}+\sqrt{72}-\sqrt{2} ?

1. 2\sqrt{30}
2. 7\sqrt{8}
3. 10\sqrt{2}
4. 11\sqrt{2}

Solución:

Primero, debemos expresar cada uno de los radicandos como el producto de factores primos, ordenados de tal manera que, el exponente de dichos factores primos sea múltiplo del índice de la raíz, en este caso 2.

Descomposición en factores del 50.

50=2*{5}^{2}

Descomposición en factores del 72.

72=2*{2}^{2}*{3}^{2}

Sustituimos.

\sqrt{50}+\sqrt{72}-\sqrt{2}=\sqrt{2*{5}^{2}}+\sqrt{2*{2}^{2}*{3}^{2}}-\sqrt{2}

Separamos las raíces.

\sqrt{2*{5}^{2}}+\sqrt{2*{2}^{2}*{5}^{2}}-\sqrt{2}=\sqrt{2}\sqrt{{5}^{2}}+\sqrt{2}\sqrt{{2}^{2}}\sqrt{{3}^{2}}-\sqrt{2}

Eliminamos raíz con potencia al cuadrado.

\sqrt{2}\sqrt{{5}^{2}}+\sqrt{2}\sqrt{{2}^{2}}\sqrt{{3}^{2}}-\sqrt{2}=5\sqrt{2}+6\sqrt{2}-\sqrt{2}

Sumamos y restamos términos semejantes.

5\sqrt{2}+6\sqrt{2}-\sqrt{2}=10\sqrt{2}

Comparando con las opciones del problema, escogemos como respuesta correcta a la opción C.