Guía UAM CBS: Ciencias biológicas y de la salud | Matemáticas resuelta

¡Hola aspirante! En este tutorial vamos a resolver los ejercicios de matemáticas, que se encuentran en la guía UAM 2022, para la división de Ciencias Biológicas y de la Salud. Antes de continuar, debo recordarte desarrollar los reactivos por tu cuenta antes de consultar la respuesta.

A continuación, te dejo un resumen de la convocatoria UAM con la información más resaltante.

Estructura del examen de ingreso UAM 2022

Esta prueba de ingreso diseñada por la Universidad Autónoma Metropolitana, se divide en dos partes, cada una con una extensión de 40 reactivos.

La primera parte del examen, tiene preguntas sobre razonamiento matemático y razonamiento verbal. La segunda, denominada prueba de conocimientos específicos, tiene un contenido que depende de la división a la que pertenezca tu carrera.

En el caso de Ciencias Biológicas y de la Salud (CBS), las preguntas están divididas entre: química, biología y física.

A continuación, te dejo un resumen muy a grandes rasgos de los sub temas incluidos en cada asignatura.

Biología

Física

Química

Resumen de reactivos en cada parte del examen.

Área	Reactivos	Porcentaje
Razonamiento verbal	20	25%
Razonamiento matemático	20	25%
Conocimientos específicos	40	50%
Total	80	100%

Temario de Matemáticas UAM CBS

Puedes consultar el temario exacto de matemáticas para el examen de ingreso a la UAM por la división de Ciencias Biológicas y de la Salud.

Aritmética

• Mínimo común múltiplo y máximo común divisor.
• Operaciones con fracciones numéricas.

Álgebra

• Términos semejantes y uso del paréntesis.
• Leyes de los exponentes y radicales.
• Razones y proporciones; porcentajes y regla de tres.
• Operaciones con polinomios (enfatizando productos y cocientes).
• Productos notables.
• Factorización.
  Operaciones con fracciones algebraicas.
• Sistemas de ecuaciones lineales.
• Ecuaciones de segundo grado y ecuaciones que se reducen a ecuaciones de segundo grado.

Trigonometría

• Triángulos semejantes.
• Teorema de Pitágoras.
• Medida de ángulos.
• Relación entre grados y radianes.
• Funciones trigonométricas, cálculos de los valores de las funciones trigonométricas en ángulos notables (45, 60, 90 y 180) y la mitad y el doble de ángulos.
• Identidades trigonométricas.
• Leyes de adición.
• Ley de los senos.
• Ley de los cosenos.
• Aplicaciones diversas usando triángulos y funciones
• trigonométricas.

Geometría analítica

• Plano euclidiano.
• Distancia entre dos puntos.
• Coordenadas del punto medio de un segmento.
• Pendiente de una recta.
• Ecuación de la recta.
• Intersección de rectas.
• Ecuación y elementos principales de la circunferencia.
• Ecuación y elementos principales de la parábola.
• Ecuación y elementos principales de la elipse.
• Ecuación y elementos principales de la hipérbola.

Calculo diferencial e integral

• Derivadas de sumas, productos, cocientes y potencias de funciones.
• Integrales inmediatas.

Logaritmos, operaciones con exponentes

• Logaritmos, operaciones con exponentes.

Medidas de tendencia central y dispersión

• Medidas de tendencia central y dispersión.

Guía UAM CBS de Matemáticas resuelta

Pasamos finalmente con la solución de los reactivos de matemáticas, que se encuentran en la guía para el examen de ingreso a la UAM por la división Ciencias Biológicas y de la Salud.

Reactivo 77: Fracciones

¿Cuál es el número qué es las \frac{2}{3} partes de \frac{1}{2} del doble de 6?

1. 4
2. 5
3. 10
4. 6
5. 2

Solución:

Debemos calcular el valor de un número cualquiera x , que es igual a la relación entre números fracciones, indicada por el enunciado.

En este tipo de problemas, debemos resolver desde el final hacia el inicio. Comenzamos con doble de 6:

2*6=12

Ahora, vamos con \frac{1}{2} del doble:

\frac{1}{2}*12=6

Finalmente, con las \frac{2}{3} partes de:

\frac{2}{3}*6=4

De esta forma, dicho número x es igual a 4.

Comparando con las opciones, seleccionamos como correcta a la A.

Reactivo 78: Encontrar el divisor

¿Por qué número se tiene que dividir 80 para que el resultado sea  \frac{3}{5} ?

1. 123\frac{1}{2}
2. 130
3. 129
4. 133\frac{1}{3}
5. 143

Solución:

En este caso, debemos calcular un número x tal que, al dividirse entre 80 \frac{80}{x} sea igual a la fracción \frac{3}{5} . Lo anterior se puede expresar mediante la siguiente igualdad:

\frac{80}{x}=\frac{3}{5}

Simplificamos.

x=\frac{80}{\frac{3}{5}}

Aplicamos la regla de la doble tortilla o doble c.

x=\frac{5*80}{3}=\frac{400}{3}

Ya que algunas de las opciones están expresadas en fracción mixta, debemos convertir nuestro resultado a esa forma. Realizamos el cociente entre el numerador y el denominador, quedando:

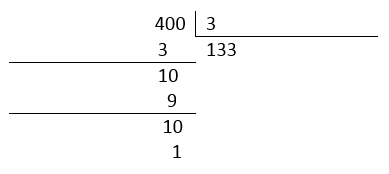
Finalmente:

x=\frac{400}{3}=133\frac{1}{3}

Comparando con las opciones, la respuesta correcta seria la D.

Reactivo 79: Operaciones con radicales

La expresión 3\sqrt{4} es igual a:

1. {4}^{2}\sqrt{2}
2. 2
3. 6
4. 8
5. \sqrt[3]{9}

Solución:

En la expresión con radical dada, sabemos que la raíz cuadrada de 4 es 2, por tanto:

3\sqrt{4}=3*2

Multiplicamos el 3 con el dos para obtener el resultado final.

3\sqrt{4}=6

Concluimos que:

La expresión 3\sqrt{4} es igual a 6.

Comparando con las opciones, queda claro que la respuesta correcta es la C.

Reactivo 80: Sistema de ecuaciones

La solución del sistema de ecuaciones \left\{\begin{array}{l} x^{2}-1=3 \\ x+y=4 \end{array}\right. es:

1. \left(-\mathrm{2,2}\right);\left(-\mathrm{2,6}\right)
2. \left(2,-2\right);\left(-\mathrm{2,6}\right)
3. \left(\mathrm{2,2}\right);\left(-2,-6\right)
4. \left(\mathrm{2,2}\right);\left(-\mathrm{2,6}\right)
5. \left(\mathrm{2,2}\right);\left(2,-6\right)

Solución:

Para resolver el sistema de ecuaciones, debemos identificar el método más conveniente que nos permita encontrar los valores de x y y . El sistema está compuesto por una ecuación de segundo grado (que no es una parábola porque no está la variable y ) y una recta.

En la primera ecuación sólo está presente la variable x , por tal razón, podríamos despejar de ella a x y luego sustituir en la segunda para hallar a y .

Despejando a x .

{x}^{2}-1=3\to {x}^{2}=4

x=\pm 2

Tenemos dos valores de x :

{x}_{1}=2 y {x}_{2}=-2

Sustituimos ahora ambos valores en la segunda ecuación para obtener la coordenada en y de cada punto.

x+y=4\to y=4-x

Para {x}_{1}=2 :

{y}_{1}=4-2=2

Para {x}_{2}=-2 :

{y}_{2}=4-\left(-2\right)=6

Los puntos de corte entre la recta y la ecuación cuadrática son:

{P}_{1}\left(\mathrm{2,2}\right) y {P}_{2}\left(-\mathrm{2,6}\right)

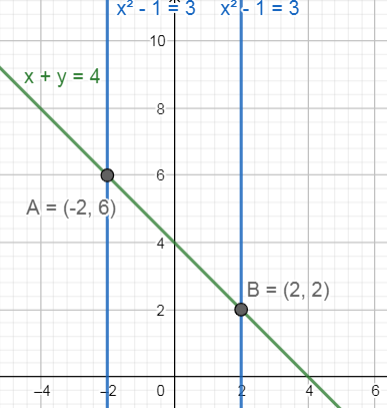
Comparando con las opciones, seleccionamos como respuesta correcta a la D.

Reactivo 81: Triángulos según sus lados

Si los lados de un triángulo miden 3 cm, 4 cm y 5 cm, el triángulo es:

1. Isósceles
2. Rectángulo
3. Acutángulo
4. Equilátero
5. Obtusángulo

Solución:

Antes de pasar a analizar si los términos de cada inciso corresponden o no con la información suministrada, podemos descartar ciertas opciones.

Por ejemplo, el triángulo no puede ser ni equilátero ni isósceles, porque ni tres ni dos de los lados miden igual. Quedan entonces descartados los incisos A y D.

Lo siguiente que podemos hacer, es aplicar el teorema de Pitágoras para comprobar si el triángulo es o no rectángulo. Elevamos el lado más largo al cuadrado y si es igual a la suma de los cuadrados de los otros dos, entonces es rectángulo.

Lado más largo.

{5}^{2}=25

Suma de los cuadrados de los otros dos.

{3}^{2}+{4}^{2}=9+16=25

¡Son iguales!

{5}^{2}={3}^{2}+{4}^{2}

El triángulo es rectángulo.

Seleccionamos como correcta la opción B.

Reactivo 82: Ecuación de la circunferencia

La ecuación de la circunferencia con centro en el punto \left(-2, 3\right) y radio 4 es:

1. {x}^{2}-3x+{y}^{2}=3
2. {x}^{2}+{y}^{2}+4x-6y=3
3. {x}^{2}+3{y}^{2}=9
4. x-y-6=16
5. -{x}^{2}+{y}^{2}-6=3

Solución:

El ejercicio nos solicita la ecuación general de la circunferencia con centro en \left(-2, 3\right) y radio igual a 4. Debemos sustituir ambos valores en la ecuación ordinaria de la circunferencia y desarrollar para obtener la general.

{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}

Sustituimos las coordenadas del centro \left(h,k\right)=\left(-\mathrm{2,3}\right) y el radio r=4 .

{\left(x+2\right)}^{2}+{\left(y-3\right)}^{2}=16

Desarrollamos.

{x}^{2}+4x+4+{y}^{2}-6y+9=16

{x}^{2}+{y}^{2}+4x-6y=3

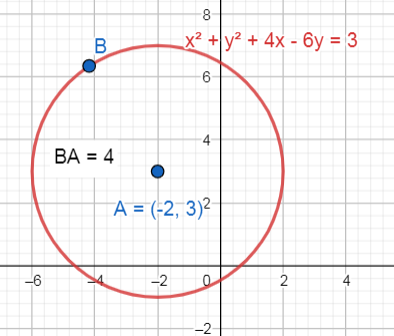
Comparando con las opciones, la respuesta correcta es la opción B.

Reactivo 83: Secciones cónicas

La ecuación \frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1 representa una:

1. Hipérbola
2. Circunferencia sobre el eje de las y
3. Elipse
4. Parábola
5. Paraboloide

Solución:

La ecuación del ejercicio representa a una elipse. No puede ser una circunferencia porque los parámetros a y b son diferentes, tampoco una hipérbola porque uno de los términos del primer miembro tendría que estar negativo y tampoco una parábola, porque ambas variables, x y y están elevadas al cuadrado.

Finalizamos el problema seleccionando como respuesta correcta a la opción C.

Reactivo 84: Sumatoria y operador sigma

La expresión {\sum }_{j=2}^{4}j  es igual a:

1. 8
2. 6
3. 7
4. 9
5. 0

Solución:

El operador sumatoria u operador sigma, permite resumir la suma sucesiva de un conjunto de valores desde un límite inferior, en este caso indicado como j=2 hasta un límite superior 4.

Para calcular el resultado, debemos sumar de 2 a 4 el valor obtenido de sustituir dicho rango de números en j de forma consecutiva.

{\sum }_{j=2}^{4}j =2+3+4=9

La sumatoria de 2 a 4 de j es igual a 9.

Comparando con las opciones, seleccionamos como correcta a la D.

Reactivo 85: Derivada de una función

La derivada de la función \ln \left(x\right)  con respecto a x es:

1. ln \left(x\right) 
2. \frac{1}{x}
3. \frac{4}{x}
4. \frac{1}{{x}^{2}-1}
5. 0

Solución:

Antes de pasar a derivar cualquier función, debemos identificar que formula y propiedades de la derivada podemos aplicar. En este caso, se trata únicamente de la función logaritmo natural de x , cuya fórmula de derivación es:

\frac{d\left[ln \left(f\left(x\right)\right) \right]}{dx}=\frac{{f}^{\text{'}}\left(x\right)}{f\left(x\right)}

f\left(x\right)=x , por lo tanto:

\frac{d\left[ln \left(x\right) \right]}{dx}=\frac{{x}^{\text{'}}}{x}

La derivada de la variable es igual a 1.

\frac{d\left[ln \left(x\right) \right]}{dx}=\frac{1}{x}

Comparando con las opciones del problema, seleccionamos como correcta a la B.