Bienvenido a esta cuarta etapa de nuestro recorrido por el abordaje del área de Razonamiento Matemático, uno de los componentes más importantes que verás presente en el examen de admisión del Instituto Politécnico Nacional. Si has llegado hasta acá, significa que realmente estás interesado en obtener buenos resultados, así que te motivamos a continuar, ya que tu esfuerzo te guiará al éxito que tanto quieres, ¡Continuemos!

Esta guía en la que resolvemos ejercicios de Razonamiento Matemático del IPN aborda un total de 50 ejercicios, los cuales están postulados en la Guía oficial del IPN.
Para que tengas la posibilidad de realizar tus estudios a través de varias sesiones de preparación, hemos separado esta guía en cinco partes. De esta manera, en este post te encontrarás con los ejercicios resueltos del 31 al 40. Dejando esto claro, recuerda que el examen de admisión aborda otras áreas de conocimiento, así que no dejes ninguna en segundo plano y prepárate lo mejor posible.
¿Qué viene en el examen del IPN?
El Instituto Politécnico Nacional plantea a sus aspirantes un examen de admisión de un total de 130 preguntas, las cuales deben ser resueltas en 160 minutos (dos horas y media). Asimismo, dicha prueba se separa en dos etapas. La primera aborda reactivos de matemáticas y lengua, mientras que la segunda, se enfoca en Física, Química y Biología.
Ahora, para que conozcas mejor este examen y seas capaz de prepararte a tiempo, te mostramos la cantidad de preguntas que comprende cada área de conocimiento en evaluación:
- 50 preguntas de matemáticas.
- 40 preguntas de comunicación.
- 10 preguntas de biología.
- 15 preguntas de química.
- 15 preguntas de física.
Dejando claro el punto anterior, damos paso a concentrarnos al 100% en la resolución de nuestra cuarta parte de la guía resuelta de ejercicios de Razonamiento Matemático del IPN:
Reactivo 31: Figuras con igual volumen
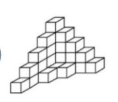
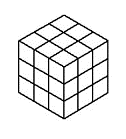
Identificar la figura con el mismo volumen que el siguiente cubo:
Solución:
Para encontrar la respuesta correcta, debemos contar de cuántos cubos pequeños está compuesto el cubo de la figura. Con una inspección rápida, sabemos que es un cubo de 3x3x3, es decir compuesto por 27 cubos pequeños.
Solo nos queda contar de cuantos cubitos está compuesto cada inciso, el que tenga la misma cantidad que la figura original, será la respuesta correcta.
Opción A.
Esta figura está compuesta por 28 cubos. 10 en cada escalera lateral, 5 en la columna central y 3 en el escalón interno. No posee el mismo volumen que el cubo.
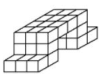
Opción B.
Se compone de 30 cubos pequeños. Es una figura con un total de 10 filas de 3 cubos, que dan un total de 30. No cumple con el requerimiento.
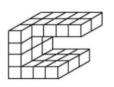
Opción C.
Está constituida por 7 filas de 3 cubitos y 4 filas de 2, arrojando un total de 29 cubitos. No cumple con el requerimiento.
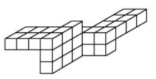
Opción D.
Está compuesta por un total de 6 filas con 2 cubitos y 5 filas de tres cubitos, arrojando un total de 27 cubitos, igual que el cubo de la figura original.
Concluimos entonces que la figura del inciso d) tiene el mismo volumen que el cubo de la imagen.
Reactivo 32: Figura formada por cortes
Identificar la figura que se forma al realizar el corte que se indica por las líneas punteadas rojas y desdoblar la hoja:
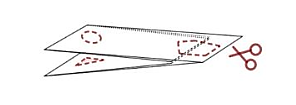
Solución:
Identifiquemos como quedarán dispuestos los cortes en la hoja luego de desdoblarla. Comencemos por el pentágono cerca del doblez, lo primero que notamos es que los pentágonos quedan separados en su base.
Además, los extremos doblados hacia el interior de la hoja quedan con un triángulo que apunta hacia el interior. Tanto el círculo como el triángulo quedan repetidos en un mismo lado y separados una cierta distancia.
Comparando toda esta descripción, la figura resultante debe ser la del inciso c).


Reactivo 33: Cantidad de cubos
¿Cuántos cubos en blanco hay en la figura, considerando los planos paralelos y sus partes interiores?

- 6
- 7
- 8
- 9
Solución:
En este caso, el problema nos indica que consideremos todas las caras del cubo. Si posee 6 caras y en cada una de ellas se visualiza un cubo blanco, hay 6 cubos blancos en total. Además, en el interior del cubo, exactamente en la zona central queda espacio para un último cubo blanco.
Concluimos entonces que debe haber un total de 7 cubos blancos, 6 visibles en cada cara y uno en el centro del cubo. Comparando con las opciones del problema, la respuesta correcta es la b).
Reactivo 34: Dobleces en una hoja
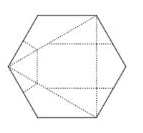
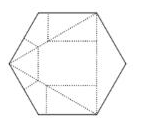
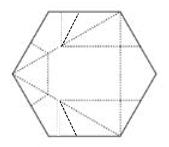
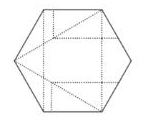
Identificar la figura que muestra las marcas de los dobleces realizados sobre la hoja:
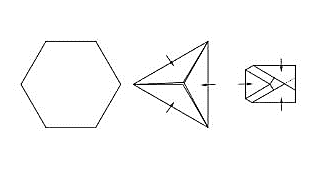
Solución:
Analicemos cómo quedan las marcas en cada doblez y cómo quedan unos respecto de otros. Primero, iniciamos por doblar los bordes hasta formar un triángulo.
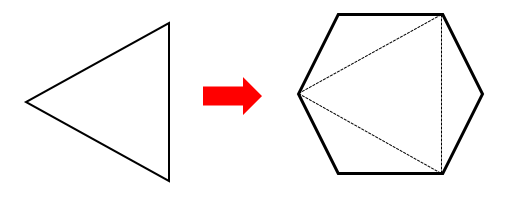
Estas son las primeras marcas que se generan al doblar los bordes. Luego se dobla la punta superior hacia adentro y las de los costados de tal forma que el doblez quede perpendicular a la base del triángulo.
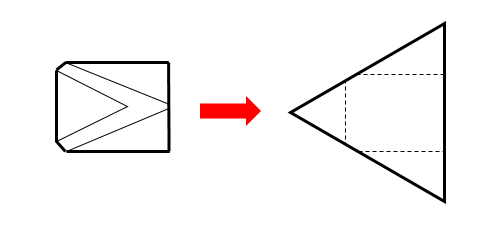
Al desdoblar en un hexágono el triángulo, las marcas de la punta izquierda en el interior deben ser verticales, por el contrario las de los bordes deben quedar inclinadas porque se han doblado previamente con cierto ángulo.
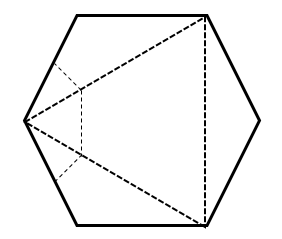
Ahora, los dobleces en las otras puntas dejarán una marca horizontal en la zona interna del triángulo y continuarán sin inclinarse al borde derecho del hexágono porque el ángulo entre ambos es 90°.
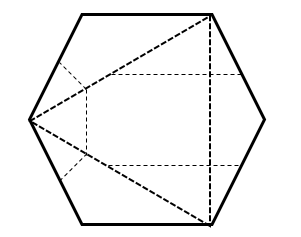
Respecto de los dobleces en los bordes superior e inferior del hexágono, la línea será inclinada porque ambos dobleces se hacen en ángulos distintos.
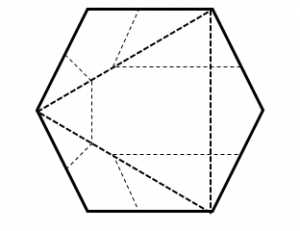
Comparando con las opciones del problema, la respuesta correcta es la c).
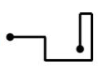
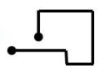
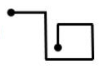
Reactivo 35: Recorrido correcto
Si el norte está hacia la parte superior de esta página ¿Cuál de los siguientes mapas representa mejor la ruta dada por las indicaciones? El número indica la cantidad de kilómetros que se deben avanzar en la dirección proporcionada.
- 2 al norte
- 2 al este
- 3 al sur
- 4 al oeste
- 2 al norte
- 3 al oeste
Solución:
En base a la referencia que se nos indica en el enunciado, podemos seguir el camino indicado a partir de las indicaciones en cada inciso.
2 al norte.
2 al este.
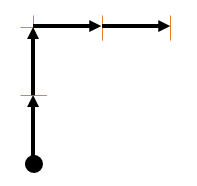
3 al sur.
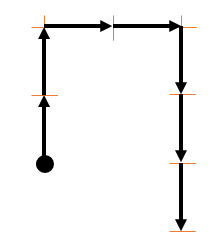
4 al oeste.
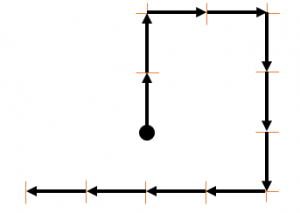
2 al norte.
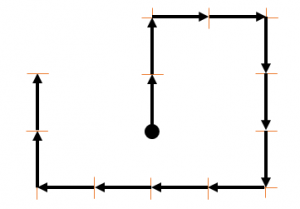
3 al oeste.
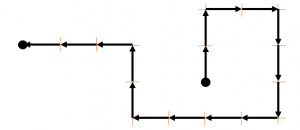
Comparando este recorrido con las opciones del problema, la respuesta correcta es la c).
Reactivo 36: Problemas matemáticos
Se tienen tres pedazos de madera: uno de encino de 15 cm de largo, uno de ébano de 10 cm de largo y uno de cerezo de 20 cm de largo. Se desea dividir todos los pedazos en partes iguales ¿Cuánto miden estos nuevos trozos y cuantos trozos en total se obtienen?
- 5 cm y 60 trozos
- 60 cm y 5 trozos
- 5 cm y 9 trozos
- 60 cm y 18 trozos
Solución:
Este problema podemos resolverlo fácilmente al descomponer en factores las longitudes de los pedazos de madera, el múltiplo común en las tres medidas será la longitud de los trozos.
El 10 puede descomponerse como:
10=2 \cdot 5
El 15 puede descomponerse como:
15=3 \cdot 5
El 20 puede descomponerse como:
20=4 \cdot 5
Es decir, 10, 15 y 20 tienen como múltiplo común al 5, por tanto los tres pedazos deben cortarse en trozos de 5 cm. Por otro lado, el de ébano puede dividirse en 2 trozos de 5 cm, el de encino en 3 trozos de 5 cm y el de cerezo en 4 trozos de 5cm.
Concluimos entonces que los pedazos de 10, 15 y 20 cm se pueden dividir en partes de 5 cm, sumando un total de 9 trozos. Comparando con las opciones de problema, la respuesta correcta es la c).
Reactivo 37: Producto entre números
Al multiplicar \frac{4}{3} por cierto número se obtiene \frac{2}{15} ¿Cuál es ese número?
- \frac{1}{10}
- \frac{8}{45}
- \frac{1}{5}
- \frac{2}{3}
Solución:
La frase enunciada en el enunciado puede escribirse algebraicamente como:
\frac{4}{3} \cdot x=\frac{2}{15}
Y se lee como: \frac{4}{3} multiplicado por un número x , es igual a \frac{2}{15} . Para encontrar el valor del número x , se aplica un simple despeje.
\frac{4}{3} \cdot x=\frac{2}{15} \rightarrow x=\frac{3}{4} \cdot \frac{2}{15}=\frac{1}{10}
Ese número debe ser \frac{1}{10} . Comparando con las opciones del problema, la respuesta correcta es la a).
Reactivo 38: Progresiones geométricas
Determinar la expresión del término general de una sucesión geométrica de razón 6, tal que la suma de los primeros tres términos sea 5.
- a_{n+2}=6 a_{1}, a_{1}=\frac{43}{5}
- a_{n+1}=6^{n+1} a_{1}, a_{1}=\frac{43}{5}
- a_{n+1}=6^{n+2} a_{1}, a_{1}=\frac{5}{43}
- a_{n+1}=6^{n} a_{1}, a_{1}=\frac{5}{43}
Solución:
Como sabemos, el término general de una progresión (o sucesión de forma general) geométrica se define como:
a_{n}=a_{1} \cdot r^{n-1}
Para todo n=1,2,3, \ldots O también como:
a_{n+1}=a_{1} \cdot r^{n}
Para todo n=0,1,2,3, \ldots
En este caso, trabajaremos con la segunda definición. El problema nos indica que el valor de la razón r=6 pero no nos dice nada sobre a_{1} , la única información adicional que tenemos es que la suma de los tres primeros términos es 5.
a_{1}+a_{2}+a_{3}=5
Si sustituimos en cada término el valor correspondiente de n nos queda que:
a_{1}=a_{1} \cdot 6^{0}=a_{1}
a_{2}=a_{1} \cdot 6^{1}=6 a_{1}
a_{3}=a_{1} \cdot 6^{2}=36 a_{1}
Sustituyendo queda:
a_{1}+6 a_{1}+36 a_{1}=5
Simplificamos.
43 a_{1}=5
a_{1}=\frac{5}{43}
De esta manera, el término general de la sucesión geométrica es:
a_{n+1}=\frac{5}{43} \cdot 6^{n}
Donde:
r=6 \text{ y } a_{1}=\frac{5}{43}
Comparando con las opciones del problema, la respuesta correcta es la d).
Reactivo 39: Perímetro de figuras planas
La figura se forma con semicircunferencias ¿Cuál es el perímetro de la región sombreada?
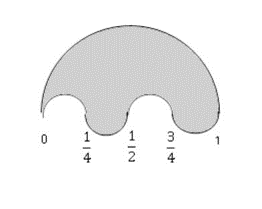
- \pi
- 2 \pi
- 3 \pi
- 4 \pi
Solución:
Para calcular el perímetro de una circunferencia podemos emplear la fórmula:
s=d \pi
Donde d es el diámetro de la circunferencia. Como necesitamos el perímetro que encierra a toda el área sombreada, la longitud total es la suma de los semi-perímetros de todas las semicircunferencias presentes.
Cómo está formada por 5 semicircunferencias, el perímetro de puede expresar como:
s=\frac{d_{1} \pi}{2}+\frac{d_{2} \pi}{2}+\frac{d_{3} \pi}{2}+\frac{d_{4} \pi}{2}+\frac{d_{5} \pi}{2}
Cada uno está dividido por 2 debido a que solo hay semicircunferencias. Además, d_{1}, d_{2}, \ldots hacen referencia al diámetro de cada semicircunferencia, enumeradas como sigue:
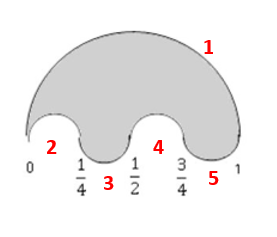
Los diámetros se pueden calcular restando el extremo mayor menos el extremo menor de la semicircunferencia en cuestión.
d_{1}=1-0=1
d_{2}=\frac{1}{4}-0=\frac{1}{4}
d_{3}=\frac{1}{2}-\frac{1}{4}=\frac{1}{4}
d_{4}=\frac{3}{4}-\frac{1}{2}=\frac{1}{4}
d_{5}=1-\frac{3}{4}=\frac{1}{4}
Sustituimos y calculamos el perímetro solicitado.
s=\frac{(1) \pi}{2}+\frac{\left(\frac{1}{4}\right) \pi}{2}+\frac{\left(\frac{1}{4}\right) \pi}{2}+\frac{\left(\frac{1}{4}\right) \pi}{2}+\frac{\left(\frac{1}{4}\right) \pi}{2}=\frac{\pi}{2}+\frac{\pi}{2}=\pi
El perímetro de toda la figura es \pi .
Comparando con las opciones que ofrece el problema, la respuesta correcta es la a).
Reactivo 40: Lenguaje natural a lenguaje algebraico
¿Cuál es el número cuya tercera parte, disminuida en 2, es igual a la quinta parte del mismo número aumentada en 4?
- 15
- 45
- 90
- 180
Solución:
Para resolver el problema, debemos convertir la relación de un número, al que denominaremos x de lenguaje natural a lenguaje algebraico, es decir a una ecuación. Analizaremos la frase por partes para deducir la ecuación y finalmente despejar su valor.
Cuál es el número cuya tercera parte, disminuida en 2… Se puede escribir como:
\frac{x}{3}-2
La tercera parte de x menos 2.
…es igual a la quinta parte del mismo número aumentada en 4… Se escribe como:
\frac{x}{3}-2=\frac{x}{5}+4
Ahora, solo queda despejar el valor de x .
\frac{x}{3}-\frac{x}{5}=2+4
\frac{2 x}{15}=6
x=6 \cdot \frac{15}{2}=45
El número que cumple con la descripción hecha en el problema es el 45. Comparando con las opciones, la respuesta correcta es la b).