En caso de que estés interesado en prepararte para el examen de admisión de la poderosa IPN, quedas invitado a resolver junto a nosotros, la guía completa de razonamiento matemático del IPN. Ten en cuenta que tu preparación te ayudará a lograr tu meta de ser aceptado en la carrera que apliques, así que ¡Adelante!
Esta serie de post enfocada en matemática analítica del IPN comprende un total de 50 ejercicios, así que podrás ver la resolución de cada uno aquí.
Para ayudarte a que puedas dividir tus sesiones de forma óptima, hemos dividido nuestra guía en cinco partes. En este caso, te encuentras en la primera parte, donde abordaremos los ejercicios del 1 al 10 en Razonamiento Matemático. Dicho esto, te invitamos a empezar tu preparación, ya que no debes olvidar que sólo tendrás 160 minutos para presentar esta prueba.
¿Qué viene en el examen del IPN?
El Instituto Politécnico Nacional plantea un examen de admisión compuesto de 130 reactivos, los cuales se desglosan en cinco áreas de conocimiento distintas. Además, esta prueba se separa en dos etapas, la primera cuenta con preguntas de matemáticas y comunicación. Luego, la segunda se enfoca en preguntas de Física, Química y Biología.
Para que conozcas cómo es la distribución de preguntas en cada una de estas áreas de estudio, acá te mostramos más detalles:
- 50 preguntas de matemáticas.
- 40 preguntas de comunicación.
- 10 preguntas de biología.
- 15 preguntas de química.
- 15 preguntas de física.
Dejando claro este aspecto, es momento dar inicio a nuestra primera parte de la guía de Razonamiento Matemático del IPN.
Reactivo 1: Sucesión Numérica
Determinar el elemento que continúa en la sucesión:
132,253,374,495,5116, \ldots
- 6107
- 6117
- 6127
- 6137
Solución:
Los problemas de razonamiento matemático se resuelven identificando una ley u operación matemática que se aplica sobre los elementos para obtener el siguiente término de la sucesión. No siempre es evidente la ley aplicada, puede ser una operación aritmética o una combinación de ellas, aplicadas entre términos contiguos o sobre sus dígitos.
En este problema, se nos da una sucesión de números de la que debemos encontrar el siguiente elemento.
132,253,374,495,5116, \ldots
Probemos restando elementos contiguos para identificar si la ley es la suma de una constante.
253-132=121
374-253=121
495-374=121
5116-495=4621
La diferencia entre términos se mantiene constante hasta 5116-495 donde incrementa enormemente de 121 a 4621, por lo tanto no es esta la ley.
Probemos ahora identificando cómo se incrementa cada dígito entre elementos contiguos de la serie.
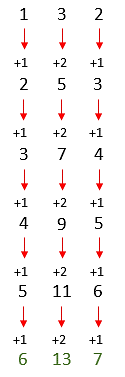
En efecto, cada elemento incrementa según se suman 1, 2 y 1 a cada dígito respectivamente. Siguiendo dicha ley, el elemento que precede a 5116 es 6137. Comparando con las opciones del problema, la respuesta correcta es la d).
Reactivo 2: Elemento faltante en la sucesión
Completar la siguiente sucesión: 1,9,25,49, \_\_\_\_, 121,169
- 72
- 75
- 78
- 81
Solución:
En este caso, a simple vista podemos identificar que los elementos no incrementan al sumar una ley constante, porque el salto entre elementos contiguos es abrupto. Lo siguiente que podemos probar es la multiplicación por una constante. Si dividimos términos contiguos y el resultado se mantiene, entonces esa es la ley.
\frac{9}{1}=9
\frac{25}{9}=2.77 \ldots
\frac{49}{25}=1.96
\vdots
Es claro que el cociente no arroja un número constante entre elementos. Lo siguiente que podemos intentar es que los números estén elevados a una potencia ya que 3^{2}=9,5^{2}=25,7^{2}=49 , es decir, la sucesión es el cuadrado de los números impares incluido el 1.
Si los números impares son:
1,3,5,7,9,11,13, \ldots\{2 n-1\}
El elemento faltante en la sucesión es el cuadrado del 9, es decir 81.
1,9,25,49,81,121,169
Como dato extra, el término general de la sucesión sería a_{n}=\left\{(2 n-1)^{2}\right\} . Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).
Reactivo 3: Progresiones aritméticas
Seleccionar el par de números que completan, respectivamente, la siguiente sucesión:
\pi, \frac{3 \pi}{2}, \_\_\_\_,\frac{5 \pi}{2}, \_\_\_\_, …
- 2 \pi, 3 \pi
- 3 \pi, 2 \pi
- -2 \pi, 3 \pi
- -3 \pi, 2 \pi
Solución:
En este problema existen 2 elementos faltantes en la sucesión, pero conocemos a dos de ellos que son contiguos y que nos servirán para encontrar la ley. Intentemos restar a \frac{3 \pi}{2} con \pi , si el resultado permite recrear la sucesión con el elemento \frac{5 \pi}{2} en el lugar correcto y completando los espacios faltantes, esa es la ley de la sucesión.
\frac{3 \pi}{2}-\pi=\frac{\pi}{2}
Probemos ahora recrear la sucesión sumando \frac{\pi}{2} a cada elemento para obtener el siguiente.
\pi+\frac{\pi}{2}=\frac{3 \pi}{2}
\frac{3 \pi}{2}+\frac{\pi}{2}=2 \pi
2 \pi+\frac{\pi}{2}=\frac{5 \pi}{2}
\frac{5 \pi}{2}+\frac{\pi}{2}=3 \pi
En efecto \frac{5 \pi}{2} aparece en el lugar correcto y los elementos faltantes son 2 \pi \text { y } 3 \pi respectivamente. Comparando con las opciones que ofrece el problema, la respuesta correcta es la a).
Reactivo 4: Sucesiones numéricas
Seleccionar el número que completa, respectivamente, la siguiente sucesión:
1, \frac{3}{2}, \frac{7}{4}, \frac{15}{8}, \frac{31}{16}, \_\_\_\_
- \frac{65}{32}
- \frac{64}{32}
- \frac{63}{32}
- \frac{61}{32}
Solución:
Por un lado, los denominadores incrementan en factores de dos. Es decir, el siguiente elemento es el doble del anterior.
Denominadores de la secuencia:
1,2,4,8,16, \ldots
Ya que la secuencia comienza en 1, el siguiente denominador será el doble, es decir 2. El tercer elemento será el segundo multiplicado por 2, es decir 4 y así sucesivamente. En esta línea de ideas, el denominador del elemento faltante es:
2 * 16=32
Los numeradores pueden ser expresados como el numerador de la fracción anterior sumado al denominador de la fracción actual:
1, \frac{3}{2}, \frac{7}{4}, \frac{15}{8}, \frac{31}{16}, \ldots
1, \frac{1+2}{2}, \frac{3+4}{4}, \frac{7+8}{8}, \frac{15+16}{16}, \ldots
Con esto, podemos asegurar que el numerador de la fracción faltante es:
31+32=63
Elemento restante:
\frac{63}{32}
Finalmente, podemos completar la secuencia de números fraccionarios:
1, \frac{3}{2}, \frac{7}{4}, \frac{15}{8}, \frac{31}{16}, \frac{63}{32}
Según las opciones que ofrece el problema, la respuesta correcta es la c).
Reactivo 5: Sucesiones alternadas
¿Cuál será el término faltante en la siguiente sucesión?
-\frac{1}{7}, \frac{1}{49}, \_\_\_\_\_,\frac{1}{2401}
- -\frac{1}{334}
- -\frac{1}{304}
- -\frac{1}{433}
- -\frac{1}{343}
Solución:
Se conoce como sucesión alternada, aquella en la que sus términos cambian de positivo a negativo a medida que se desarrolla la sucesión. Como el primer elemento es el que está negativo, el segundo es positivo y el tercero negativo, ahora solo nos queda determinar la ley entre los términos.
A simple vista, es claro que no es una progresión aritmética porque la resta entre términos contiguos no es una constante.
Inspeccionando los denominadores en cada una de las fracciones, el segundo puede expresarse como 7^{2} y el cuarto como 7^{4} . De esta forma, la ley de cambio en la sucesión es multiplicar por \frac{1}{7} el término actual para obtener el siguiente.
-\frac{1}{7}, \frac{1}{7^{2}}, \_\_\_\_\_, \frac{1}{7^{4}}
En base a esto, el tercer término de la sucesión es:
-\frac{1}{343}
Escribiendo el término faltante, la sucesión queda como:
-\frac{1}{7}, \frac{1}{49},-\frac{1}{343}, \frac{1}{2401}
Comparando con las opciones que ofrece el problema, la respuesta correcta es la d). Como dato extra, el término general de la progresión geométrica es:
a_{n}=\left\{(-1)^{n} \frac{1}{7^{n}}\right\}
Reactivo 6: Progresiones Geométricas
Completar la siguiente progresión geométrica:
3,15,75, \_\_\_\_,1875, \ldots
- 275
- 365
- 375
- 475
Solución:
En este caso, el problema nos da una pista importante respecto a la naturaleza de la sucesión: es una progresión geométrica. Es decir, el elemento siguiente se obtiene multiplicando al elemento actual por una razón.
a_{n}=\left\{a \cdot r^{n-1}\right\}
Como el primer elemento de la progresión es 3 y además, para n=1 \rightarrow n-1=0 entonces r^{0}=1 obtenemos que la constante a=3 .
Por otro lado, el segundo elemento de la progresión es 15, número que se obtiene al multiplicar 3 por 5. De esa forma, sabemos que la razón de la progresión geométrica es r=5 .
a_{n}=\left\{3 \cdot 5^{n-1}\right\}
Comprobamos nuestro resultado:
n=1 \rightarrow a_{1}=3
n=2 \rightarrow a_{2}=3 \cdot 5^{1}=15
n=3 \rightarrow a_{3}=3 \cdot 5^{2}=75
n=4 \rightarrow a_{4}=3 \cdot 5^{3}=375
n=5 \rightarrow a_{5}=3 \cdot 5^{4}=1875
Concluimos entonces que el término restante es 375. Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).
Reactivo 7: Sucesiones numéricas
Determinar el siguiente número de la sucesión:
2,5,10,17,26,37, \_\_\_\_
- 49
- 50
- 51
- 52
Solución:
Ya que el incremento entre términos contiguos no es exagerado, podemos iniciar pensando que la ley proviene de la suma de alguna cantidad de un término a otro. Dispondremos a cada término como la suma del término anterior y otra cantidad.
2,5,10,17,26,37 \rightarrow 1+1,2+3,5+5,10+7,17+9,26+11, \ldots
De lo anterior, podemos observar que el elemento siguiente se forma por la suma del elemento anterior y un número impar correspondiente partiendo desde el 1, es decir 1, 3, 5, 7, 9, 11.
a_{n}=a_{n-1}+2 n-1
Por tanto, si el término anterior al faltante es 37 y el impar correspondiente es 13, obtenemos que:
a_{7}=37+13=50
El término faltante en la sucesión es a_{7}=50 . Comparando con las opciones que ofrece el problema, la respuesta correcta es la b).
Reactivo 8: Secuencia numérica
Determinar el número que continúa en la siguiente secuencia:
6,20,48,104, \_\_\_\_
- 180
- 200
- 216
- 222
Solución:
Para encontrar el número que continúa la secuencia, vamos a descomponer a los términos (exceptuando al primero) como la suma de su antecesor y otra cantidad.
6,6+14,20+28,48+56, \ldots
Como vemos, el término actual puede expresarse como la suma del anterior sumado a una potencia de 2 multiplicada por 7, a partir del segundo término. Es decir, que el elemento faltante es 104 (el término anterior) sumado con el doble de 56, es decir 112.
a_{5}=104+112=216
Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).
Reactivo 9: Término general de la serie
Encontrar el décimo término de una sucesión aritmética con diferencia igual a 20, tal que la suma de los primeros dos términos sea 1.
- \frac{341}{2}
- \frac{2}{341}
- -\frac{2}{341}
- -\frac{341}{2}
Solución:
Toda sucesión aritmética se describe por tener como término general a la siguiente expresión:
a_{n}=\{a+(n-1) d\}
Donde a es un número fijo y d es la diferencia. En el problema se nos da el valor que debe tener la diferencia: d=20 pero no conocemos al número fijo a , en su lugar, sabemos que la suma de los dos primeros términos a_{1}+a_{2} debe ser igual a 1. Expresado en base al término general tenemos:
a_{1}=a
a_{2}=a+d
Sumamos ambos términos.
a_{1}+a_{2}=a+a+d=1
2 a+d=1
Despejando a y sustituyendo d=20 nos queda que:
a=-\frac{19}{2}
El término general se puede expresar como:
a_{n}=\left\{-\frac{19}{2}+20(n-1)\right\}
Obtenemos finalmente al décimo término sustituyendo en la expresión general n=10 .
a_{10}=\left\{-\frac{19}{2}+20(10-1)\right\}=\frac{341}{2}
Comparando con las opciones que ofrece el problema, la respuesta correcta es la a).
Reactivo 10: Número faltante
Determinar el número faltante en la secuencia:
\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \_\_\_\_,\frac{1}{729}
- \frac{1}{191}
- \frac{1}{243}
- \frac{1}{318}
- \frac{1}{614}
Solución:
Lo primero que podemos identificar al examinar los denominadores de los términos en la secuencia, es que corresponden a potencia de 3.
\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \_\_\_\_, \frac{1}{729} \rightarrow \frac{1}{3}, \frac{1}{3^{2}}, \frac{1}{3^{3}}, \frac{1}{3^{4}}, \_\_\_\_\_, \frac{1}{3^{6}}
Por tanto, el término restante no es más que el inverso de 3 elevado a la quinta potencia, es decir \frac{1}{3^{5}}=\frac{1}{243} . La secuencia de números completa sería:
\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}, \frac{1}{243}, \frac{1}{729}
En base a las opciones ofrecidas por el problema, la respuesta correcta es la b).


