¿Tienes problemas con la guía del IPN? ¡Has llegado al lugar indicado! En este tutorial vamos a resolver los 40 ejercicios correspondientes a la parte de probabilidad y estadística de la guía IPN, para el examen de ingreso al Politécnico Nacional.

El siguiente es un resumen de la convocatoria IPN.
- Carreras ofertadas en IPN: 70+.
- Porcentaje de Aceptación: 20%.
- Preguntas en el examen de Admisión: 140 preguntas.
- Nuevos temas: historia e inglés (reading comprehension).
- Tipo: selección múltiple.
Estructura del Examen IPN
La estructura del examen ha cambiado para este. La cantidad de reactivos por asignatura varía en función al área de conocimientos de tu carrera. Las carreras en el Instituto Politécnico Nacional se dividen en 3 áreas del conocimiento:
- Ingeniería y Ciencias Físico Matemáticas IyCFM
- Ciencias Sociales y Administrativas CSA
- Ciencias Médico Biológicas CMB
La siguiente tabla muestra la estructura de reactivos por materia para cada área.
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
¿Qué tan difícil es el examen al IPN?
Llegados a este punto, puede que te hagas la pregunta: ¿qué tan difícil es entrar al IPN? La respuesta depende de un único factor: tu preparación antes del examen.
Conoce todo sobre el proceso de ingreso a la universidad en la convocatoria del IPN.
Para la convocatoria se incluyen 2 nuevas asignaturas, aumentando así la cantidad de reactivos de 130 a 140. En la guía de probabilidad y estadística se incluyen reactivos que cubren los temas de la asignatura con una complejidad moderada.
Temario probabilidad y estadística IPN
Estos son los temas de probabilidad y estadística que deberás estudiar antes de presentar el examen:
-
- Probabilidad
- Teoría de conjuntos
- Técnicas de conteo
- Espacios muestrales
- Probabilidad de un evento
- Eventos aleatorios
- Probabilidad condicional
- Eventos dependientes e independientes
- Teorema de bayes
- Estadística descriptiva
- Tablas de distribución de frecuencias
- Gráfica de datos
- Muestra y población
- Medidas de tendencia central
- Medidas de posición
- Medidas de dispersión
- Probabilidad
¿Cómo resolver la guía del IPN?
Te recomiendo examinar la bibliografía recomendada por la guía del IPN antes de pasar con los reactivos. Un error común entre los aspirantes es estudiar los temas mientras resuelven la guía.
Estudiar de esta forma te hará perder tiempo e irás a ciegas sin una metodología al estudiar.
Los siguientes hacks te ayudarán a mejorar el desempeño, resolviendo la mayor cantidad de reactivos en el menor tiempo para obtener los aciertos que necesitas para ser admitido.
- Resuelve cada parte por tu cuenta antes de checar las respuestas. Utiliza este material a modo de consulta.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
- Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo.
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico.
- Te advierto que la guía del IPN tiene algunos errores, solo en Unibetas te señalamos cuáles son.
Reactivo 1
Siendo A, B, C conjuntos no vacíos, relacionar las siguientes expresiones con su respectiva propiedad.

- 1C, 2B, 3A, 4D
- 1D, 2C, 3B, 4A
- 1C, 2D, 3A, 4B
- 1D, 2B, 3C, 4A
Solución:
Para encontrar la combinación correcta, debemos analizar las operaciones entre conjuntos con el nombre de la propiedad que estas representan. Estas propiedades junto a las operaciones debes conocerlas de memoria.
Primera expresión.
A\cup (B\cap C)=(A\cup B)\cap (A\cup C)
Se trata de la propiedad distributiva para la unión de conjuntos. Podemos obtener la expresión de la derecha si deshacemos los paréntesis y unimos al conjunto A con el B y el C . Similar a la distributiva que utilizamos en aritmética y álgebra. 1D.
Segunda expresión.
A\cup B=B\cup A
Sin demasiada justificación, esta es la propiedad conmutativa respecto a la unión de conjuntos. Tenemos entonces: 2C. En este punto hay suficiente información para concluir que la respuesta correcta es el inciso b) porque es el único que comienza 1D, 2C, …
Reactivo 2
La característica que define a los elementos que pertenecen a la unión se definen como:
- x pertenece a A \widehat{\mathrm{U}}x pertenece a B
- x pertenece a A\text{ y }x pertenece a B
- x pertenece a A \widehat{U}x no pertenece a B
- x no pertenece a A \widehat{U}x pertenece a B
Solución:
La unión entre conjuntos, es una operación que da como resultado a otro conjunto que contiene a todos los elementos de A y B . Eso significa que sí x es un elemento de la unión, este puede encontrarse en A o en B .
Haciendo una inspección a los incisos, el único que se acerca a la definición de la unión es el b), porque el resto indican la no existencia de x en alguno de los conjuntos o el opuesto de \widehat{U}x . El conector lógico “y” en el inciso b) provoca que no sea una definición estricta de la unión.
Si bien, que x pertenezca a A y a B simultáneamente es un subconjunto de la unión, no define por completo a la operación. Probablemente hubo un error de sintaxis al momento de redactar el reactivo, en lugar de “o” colocaron “y”.
Reactivo 3
Dados A=\{a,b,d,e\},B=\{b,d,f,g\} y U=\{a,b,c,d,e,f,g,h\} , determinar el conjunto \left({A}^{c}\cap {B}^{c}\right) .
- \left\{c,d\right\}
- \left\{e,f\right\}
- \left\{c,f\right\}
- \left\{c,h\right\}
Solución:
El ejercicio nos proporciona a dos conjuntos contenidos en U y una operación entre los conjuntos. Iniciamos obteniendo el complemento de los conjuntos A y B .
Recordemos que el complemento es el conjunto de todos los elementos que no se encuentran en el conjunto original, respecto al conjunto universo.
{A}^{c}=U-A=\left\{c, f, g, h\right\}
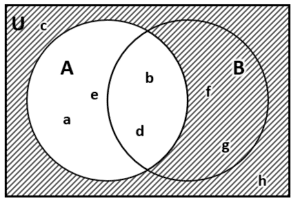
{B}^{c}=U-B=\left\{a, c, e, h\right\}
Finalmente, obtenemos la intersección de los complementos.
\left({A}^{c}\cap {B}^{c}\right)=\left\{c, f, g, h\right\}\cap \left\{a, c, e, h\right\}=\left\{c, h\right\}
Representado gráficamente:
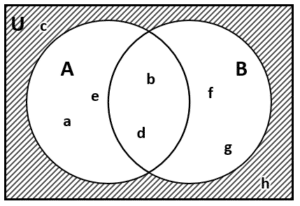
La respuesta correcta es el inciso d).
Reactivo 4
El enunciado “x pertenece al conjunto A y x pertenece al conjunto B” es una forma de representar la:
- unión
- diferencia
- intersección
- complemento
Solución:
Esta pregunta es teórica, debes conocer los conceptos básicos de teoría de conjuntos para resolverla. Examinando la frase, sabemos que hace referencia a la intersección y no a la unión, porque el conector lógico es “y” para la intersección.
Para el caso de la unión, el conector lógico de la frase es “o”. Concluimos que la respuesta correcta es el inciso c).
Reactivo 5
Dados los conjuntos A=\{\mathrm{1,2},\mathrm{3,4},a,b,c\} y B=\left\{\mathrm{5,6},7,d,e,f\right\} , respecto de U=\{\mathrm{1,2},\mathrm{3,4},\mathrm{5,6},\mathrm{7,8},9,a,b,c,d,e,f,g,h\} determinar el evento A\cap {B}^{c} .
- \left\{\mathrm{1,2},\mathrm{3,4},a,b,c,d\right\}
- \left\{\mathrm{4,5},\mathrm{6,7},c,d,e\right\}
- \left\{\mathrm{1,2},\mathrm{3,4},b,c\right\}
- \left\{\mathrm{1,2},3,a,b,c\right\}
Solución:
Iniciamos calculando el complemento del conjunto B .
{B}^{c}=U-B=\left\{1, 2, 3, 4, 8, 9, a, b, c, g, h\right\}
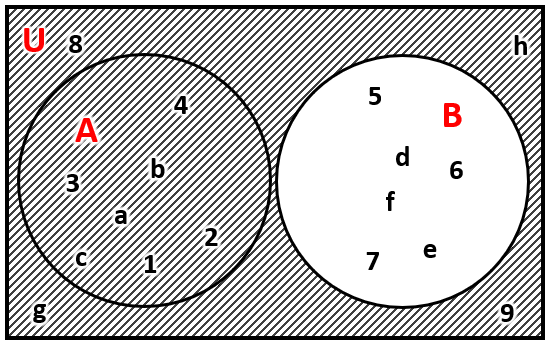
Interceptamos a los conjuntos.
A\cap {B}^{c}=\left\{\mathrm{1,2},\mathrm{3,4},a,b,c\right\}\cap \left\{1, 2, 3, 4, 8, 9, a, b, c, g, h\right\}
A\cap {B}^{c}=\left\{1, 2, 3, a, b, c\right\}
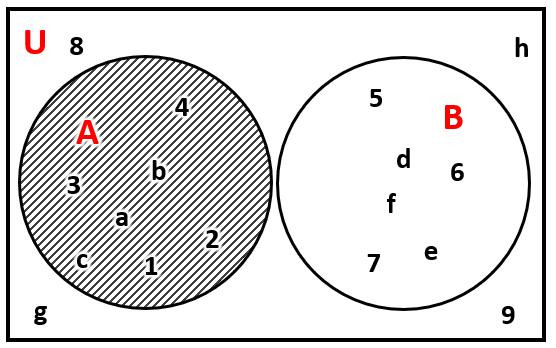
Concluimos el problema indicando como respuesta correcta al inciso d).
Reactivo 6
Relacionar el diagrama de Venn con la expresión de conjuntos que le corresponde.
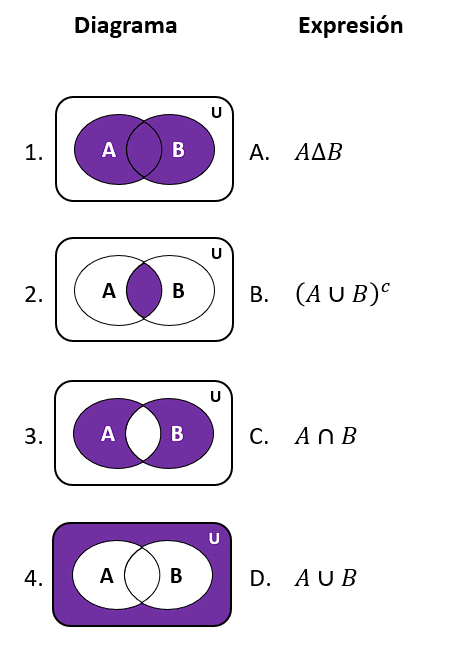
- 1D, 2A, 3B, 4C
- 1D, 2C, 3A, 4B
- 1A, 2D, 3C, 4B
- 1A, 2C, 3B, 4D
Solución:
Debemos identificar la operación efectuada sobre los conjuntos a partir de los diagramas de Venn. Aplicaremos la técnica de encontrar pareos y descartar de los incisos, de esta forma se llega a la respuesta correcta más rápido.
Gráfica del inciso 1.
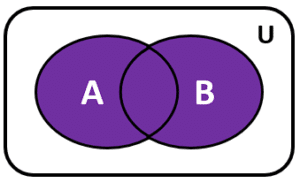
Este gráfico representa a la unión. 1D.
Gráfica del inciso 2.
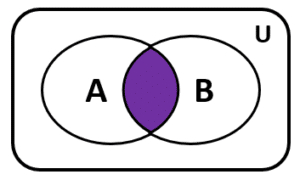
Esta gráfica representa a la región compartida por ambos conjuntos, es decir, la intersección. 2C.
Con estas dos respuestas parciales, tenemos suficiente información para concluir que la respuesta correcta es el inciso b).
Reactivo 7
Si se tienen 7 hombres y 6 mujeres y se desea formar un equipo que esté compuesto por tres hombres y tres mujeres, ¿de cuántas maneras se puede llevar a cabo la selección?
- 25200
- 700
- 330
- 55
Solución:
Debemos iniciar identificando las técnicas de conteo necesarias para resolver el problema. Tanto para los hombres como para las mujeres, no importa el orden en el que se seleccionan de 3 en 3.
Debido a que es igual un grupo de 3 hombres ordenado de la forma: José, Luis y Esteban, que: Luis, José y Esteban; los grupos de 3 se calculan como una combinación. Lo mismo aplica para las mujeres.
Grupos de hombres:
GH={C}_{3}^{7}=\frac{7!}{3!\left(7-3\right)!}=35 \mathrm{g}\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{o}\mathrm{s}
Grupos de mujeres:
GM={C}_{3}^{6}=\frac{6!}{3!\left(6-3\right)!}=20 \mathrm{g}\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{o}\mathrm{s}
Si tomamos al grupo G{H}_{1} y formamos equipo con todos los grupos de mujeres GM disponibles, se obtienen combinaciones totalmente diferentes, que si tomamos al grupo G{H}_{2} y formamos equipo con todos los grupos de mujeres.
Esto se traduce en que el total de equipos posibles se obtiene como el producto del total de grupos de hombres GH por el total de grupos de mujeres GM .
\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{p}\mathrm{o}\mathrm{s}={C}_{3}^{7}\cdot {C}_{3}^{6}=\left(35\right)\left(20\right)=700 \mathrm{e}\mathrm{q}\mathrm{u}\mathrm{i}\mathrm{p}\mathrm{o}\mathrm{s}
Se pueden crear 700 equipos.
Concluimos indicando como respuesta correcta al inciso b).
Reactivo 8
¿De cuántas maneras se puede acomodar una fila de autos si se tienen 3 rojos, 3 azules y se busca alternarlos?
- 72
- 36
- 24
- 12
Solución:
En este problema nos dicen que tenemos un conjunto de 6 carros: 3 rojos y 3 azules. En principio, vamos a diferenciar los carros uso de otros, es decir:
Carros rojos:
R=\left\{{R}_{1}, {R}_{2}, {R}_{3}\right\}
Carros azules:
A=\left\{{A}_{1},{A}_{2}, {A}_{3}\right\}
Debido a que los carros son diferentes unos de otros, la cantidad de formas de ordenar cada grupo se calcula mediante una permutación.
Orden de carros rojos.
OCR={P}_{3}=3!=6
Orden de carros azules.
OCA={P}_{3}=3!=6
Ahora, los carros deben ordenarse de forma alternada según el color. Desplazamos a uno de los colores y al otro lo ordenamos en los espacios restantes, escogemos desplazar al color azul. Los posibles desplazamientos son:
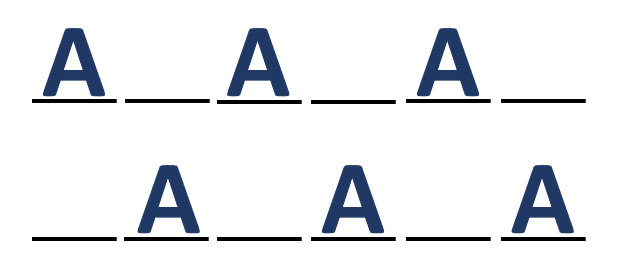
Es decir, multiplicamos por 2 al orden de carros azules.
OCA=2\left(6\right)=12
Finalmente, el total de formas en que se pueden ordenar alternadamente los carros, es igual al producto de OCR y OCA .
\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}=\left(12\right)\left(6\right)=72 \mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{s}
Los carros rojos y azules se pueden ordenar de manera alternada de 72 formas diferentes.
Seleccionamos al inciso a) como la respuesta correcta.
Reactivo 9
¿Cuál es el espacio muestral de lanzar un dado y una moneda simultáneamente?
- 24
- 12
- 10
- 8
Solución:
El espacio muestral de un experimento aleatorio, es el conjunto con todos los posibles resultados. Al tener un dado y una moneda, tenemos que los 6 posibles resultados del dado se pueden combinar con los 2 posibles resultados de la moneda.
Posibles resultados del dado.
{S}_{1}=\left\{1, 2, 3, 4, 5, 6\right\}
Posibles resultados de la moneda.
{S}_{2}=\left\{\mathrm{S}\mathrm{o}\mathrm{l},\mathrm{ }\mathrm{Á}\mathrm{g}\mathrm{u}\mathrm{i}\mathrm{l}\mathrm{a}\right\}
El espacio muestral sería:
S=\left\{1S, 1A, 2S, 2A, 3S, 3A, 4S, 4A, 5S, 5A, 6S, 6A\right\}
La amplitud del espacio muestral es de 12 posibles resultados.
La respuesta correcta es el inciso b).
Reactivo 10
En un restaurante hay un menú que incluye 3 postres, 5 platillos fuertes y tres entradas. ¿De cuántas maneras diferentes podría armar su comida una persona?
- 45
- 40
- 30
- 25
Solución:
Tengamos en cuenta que hacemos distinción entre los postres, los platos fuertes y las entradas.
Postres.
P=\left\{{P}_{1}, {P}_{2}, {P}_{3}\right\}
Platillos fuertes.
PF=\left\{P{F}_{1}, P{F}_{2}, P{F}_{3}, P{F}_{4}, P{F}_{5}\right\}
Entradas.
E=\left\{{E}_{1}, {E}_{2}, {E}_{3}\right\}
Por otra parte, una comida viene compuesta por una entrada, un plato fuerte y un postre. El total de comidas que se pueden armar se calcula como el producto del total de entradas, platos fuertes y postres.
\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{a}\mathrm{s}=\left(3\right)\left(5\right)\left(3\right)=45 \mathrm{c}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{d}\mathrm{a}\mathrm{s}
Una persona podría armar 45 comidas diferentes en el restaurante.
Concluimos indicando como respuesta correcta al inciso a).

