Continuamos resolviendo la nueva guía de estudios para el examen de ingreso en la parte de probabilidad y estadística IPN. En esta segunda parte, vamos a desarrollar los ejercicios del 11 al 20.

Recuerda estudiar la teoría relacionada con los temas de probabilidad. Sin estos conocimientos teóricos, no podrás resolver ningún reactivo.
Reactivo 11
Durante sus vacaciones, un joven pretende visitar cuatro ciudades: A, B, C y D. Tiene 5 maneras para viajar de A a B; de B a C, solo cuenta con cuatro formas y de C a D puede hacerlo de tres modos. ¿De cuántas maneras puede realizar su viaje de A a B?
- 30
- 40
- 60
- 50
Solución:
Nota: en el enunciado hay un error de redacción, la pregunta es:
¿De cuántas maneras puede realizar su viaje de A a D?
Si no, la pregunta se respondería con el dato indicado en el enunciado. Aclarado esto, la cantidad de formas que hay para ir desde A hasta D, se calcula mediante la ley del producto.
\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}=5\cdot 4\cdot 3=60\mathrm{ }\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}\mathrm{a}\mathrm{s}
El joven tiene 60 formas distintas para ir desde A hacia B.
La respuesta correcta es el inciso c).
Reactivo 12
En un aula se tienen 10 alumnos y se desea formar un grupo de 4 sin importar el orden de selección. ¿De cuántos modos se logra?
- 24
- 210
- 720
- 1040
Solución:
En el enunciado, ya nos establecen que no importa el orden al momento de formar los grupos. Esto significa que debemos utilizar combinaciones.
{C}_{n}^{m}=\frac{m!}{n!\left(m-n\right)!}
Sustituimos n=4 y m=10 .
{C}_{4}^{10}=\frac{10!}{4!\left(10-4\right)!}=\frac{10!}{4!6!}=210
Los 10 estudiantes se pueden combinar de 210 formas para crear los grupos de 4 integrantes.
La respuesta correcta es el inciso b).
Reactivo 13
Si se lanza al aire una moneda de doble cara y un dado, ¿cuántos elementos tendrá el espacio muestral?
- 6
- 1
- 12
- 36
Solución:
Para encontrar la amplitud del espacio muestral, podemos hacer el diagrama de árbol del experimento. Tengamos en cuenta que no es una moneda normal, ambas caras son iguales. Esto quiere decir que en el 100% de los lanzamientos el resultado será cara.
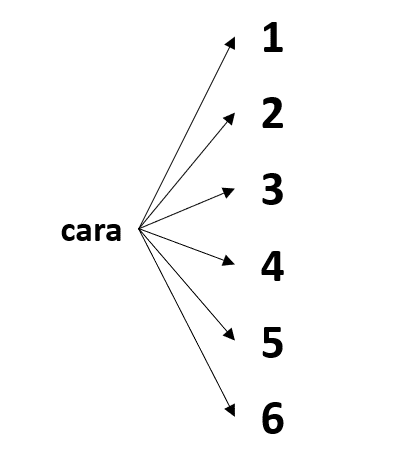
Contando todos los posibles resultados, tenemos que el espacio muestral es de 6 eventos.
La respuesta correcta es el inciso a).
Reactivo 14
Determinar los elementos del siguiente espacio muestral:
S=\left\{x\mid {x}^{4}-5{x}^{2}+4\right\}
- \left\{-2,-\mathrm{1,1},2\right\}
- \left\{-\mathrm{2,1},\mathrm{2,4}\right\}
- \left\{-\mathrm{2,1},\mathrm{2,3}\right\}
- \left\{\mathrm{1,2},\mathrm{3,4}\right\}
Solución:
Aunque el enunciado no lo indique, el conjunto S está formado por las raíces del polinomio dado.
{x}^{4}-5{x}^{2}+4=0
Para resolverlo, hacemos un cambio de variable:
q={x}^{2}
{x}^{4}-5{x}^{2}+4=0\to {q}^{2}-5q+4=0
Buscamos dos números que sumados sean -5 y que multiplicados 4; estos son: -1 y -4.
{q}^{2}-5q+4=0\to \left(q-4\right)\left(q-1\right)=0
Ahora:
{q}_{1}=4, {q}_{2}=1
Sustituimos estos resultados en la igualdad del cambio de variable.
{x}^{2}={q}_{1}\to x=\pm \sqrt{4}=\pm 2
{x}^{2}={q}_{2}\to x=\pm \sqrt{1}=\pm 1
El conjunto S quedaría:
S=\left\{-2, -1, 1, 2\right\}
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 15
Se realiza el experimento de lanzar una moneda al aire n veces. ¿De cuántas maneras puede ocurrir este experimento?
- 0
- \varnothing
- 2n
- {2}^{n}
Solución:
Hagamos un diagrama de árbol con las primeras 3 evoluciones para estudiar de forma gráfica el experimento.
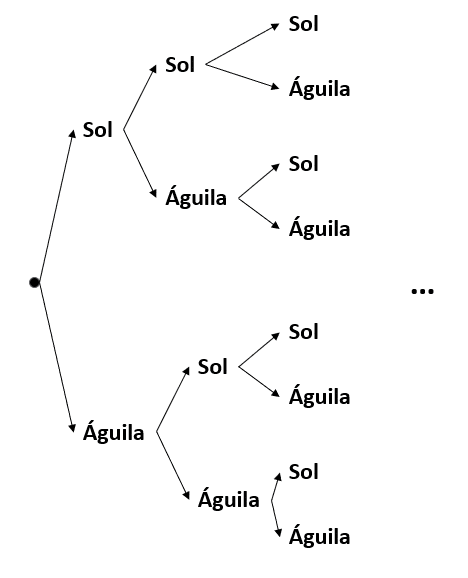
La cantidad de elementos incrementa de la forma:
2, 4, 8, \dots
Esto se puede generalizar expresando al espacio muestral como una potencia de base 2.
S=\left\{{2}^{n}\right\}, \forall n\ge 1
La respuesta correcta es el inciso d).
Reactivo 16
¿Qué probabilidad es equivalente a la expresión?
P\left({B}^{c}\cap A\right)
- P\left(A\right)-P\left(A\cup B\right)
- P\left(A\right)+P\left(A\cup B\right)
- P\left(A\right)-P\left(A\cap B\right)
- P\left(A\right)+P\left(A\cap B\right)
Solución:
Este problema se puede resolver tanto de forma gráfica como aplicando las propiedades de las operaciones entre conjuntos. Vamos a resolverlo mediante operaciones, pero al final dejaremos una figura indicando como se haría de forma gráfica.
Iniciamos sustituyendo {B}^{c}=U-B .
P\left({B}^{c}\cap A\right)=P\left(\left(U-B\right)\cap A\right)=P\left(U\cap A-B\cap A\right)
La intersección de cualquier conjunto con el universo, es igual al conjunto.
P\left(U\cap A-B\cap A\right)=P\left(A-A\cap B\right)
Finalmente:
P\left(A-A\cap B\right)=P\left(A\right)-P\left(A\cap B\right)
La respuesta correcta es el inciso c). De forma gráfica, el problema se resolvería:
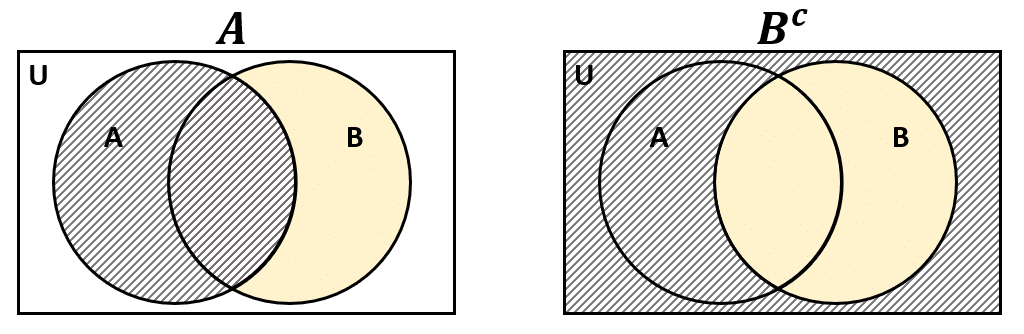
La intersección entre los conjuntos es:
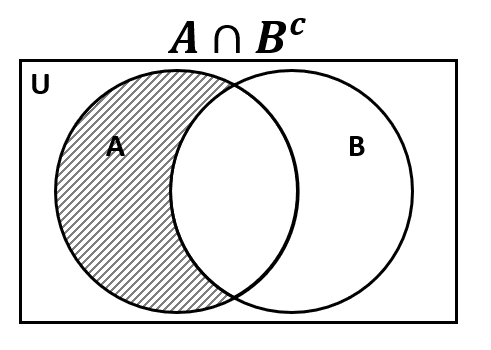
Este resultado se puede obtener al restarle la intersección A\cap B al conjunto A .
P\left(A\right)-P\left(A\cap B\right)
Reactivo 17
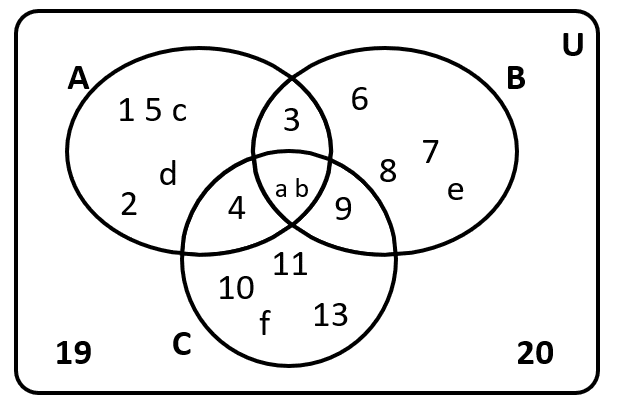
De acuerdo con la figura, donde todos los elementos de cada conjunto se consideran igualmente probables, ¿cuál es la probabilidad de que ocurra el evento C?
- P\left(A\right)=\frac{2}{5}
- P\left(A\right)=\frac{9}{20}
- P\left(A\right)=\frac{1}{5}
- P\left(A\right)=\frac{11}{20}
Solución:
En los incisos hay un error de transcripción, porque no se pide la probabilidad del evento A , sino del evento C . Hecha esta observación, continuamos con la solución.
Para calcular la probabilidad del evento C , dividimos al total de sucesos en C por el total de sucesos en el universo. A partir del gráfico tenemos:
\left\{C\right\}=8
\left\{U\right\}=20
Finalmente:
P\left(C\right)=\frac{8}{20}=\frac{2}{5}
La respuesta correcta es el inciso a).
Reactivo 18
Identificar la probabilidad que es equivalente a la siguiente expresión:
P\left({A}^{c}\cup {B}^{c}\right)
- 1+P\left(A\cup B\right)
- 1-P\left(A\cap B\right)
- 1-P\left(A\cup B\right)
- 1+P\left(A\cap B\right)
Solución:
Nota: en este reactivo hay un error en los incisos.
Para resolver esta operación entre conjuntos, utilizamos una de las leyes de Morgan.
{A}^{c}\cup {B}^{c}={\left(A\cap B\right)}^{c}
Ahora, el complemento de cualquier conjunto se calcula como:
{A}^{c}=U-A
Entonces:
{\left(A\cap B\right)}^{c}=U-A\cap B
Sustituyendo.
P\left({A}^{c}\cup {B}^{c}\right)=P\left(U-A\cap B\right)=P\left(U\right)-P\left(A\cap B\right)
Finalmente:
P\left({A}^{c}\cup {B}^{c}\right)=1-P\left(A\cap B\right)
De forma gráfica:
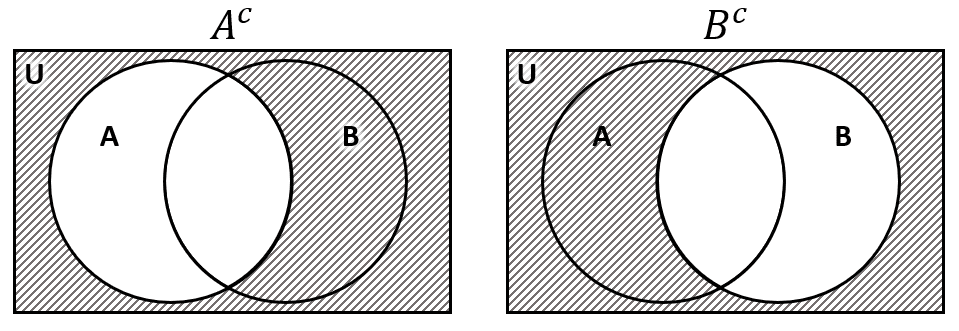
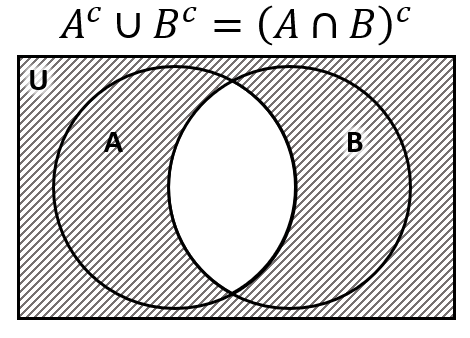
La respuesta correcta es el inciso b).
Reactivo 19
De acuerdo con la figura, donde todos los elementos de cada conjunto se consideran igualmente probables, ¿cuál es la probabilidad de que ocurra el evento (A-B) ?

- P\left(A-B\right)=\frac{3}{20}
- P\left(A-B\right)=\frac{1}{5}
- P\left(A-B\right)=\frac{3}{10}
- P\left(A-B\right)=\frac{7}{20}
Solución:
Para realizar la resta A-B podemos apoyarnos del gráfico. Recordemos que la diferencia de conjuntos da como resultado otro conjunto con los elementos del minuendo que no se encuentran en el sustraendo.
Aplicado sobre el problema, la diferencia es igual a los elementos del conjunto A que no se encuentran en el conjunto B .
A-B=\left\{1, 2, 4, 5,c, d\right\}
Este evento tiene un total de 6 sucesos. El conjunto universo tiene un total de 20 sucesos. La probabilidad P\left(A-B\right) se calcula como:
P\left(A-B\right)=\frac{6}{20}=\frac{3}{10}
Concluimos que la respuesta correcta es el inciso c).
Reactivo 20
¿Cuál de los siguientes eventos no es aleatorio?
- Elegir a una persona de una lista y ver cuál es su sexo
- Lanzar un dado y observar qué número sale
- Lanzar una moneda al aire
- Ir a la escuela todos los días
Solución:
Los experimentos aleatorios, son aquellos que se realizan en sistemas matemáticos, físicos, químicos, biológicos, sociales, … Donde las variables no se encuentran estrictamente definidas por una ley de correspondencia, pero su comportamiento se puede modelar mediante distribuciones de probabilidad.
Teniendo en cuenta esta definición y examinando los incisos, el d) no establece una relación de probabilidad. Por el contrario, establece una acción que se realiza con cierto periodo temporal y que siempre sucede.
El inciso d) muestra un evento que no es aleatorio.

