Llegamos a la tercera y última parte de la guía interactiva del EXANI II resuelta, correspondiente a Pensamiento Matemático desde el reactivo 21 hasta el 30.

Continúa estudiando para tu examen de ingreso con el resto de materiales para EXANI II que hemos diseñado para ti. Mide el tiempo que tardas en resolver las guías e intenta mejorarlos con los trucos que te dejamos a continuación.
Reactivo 21
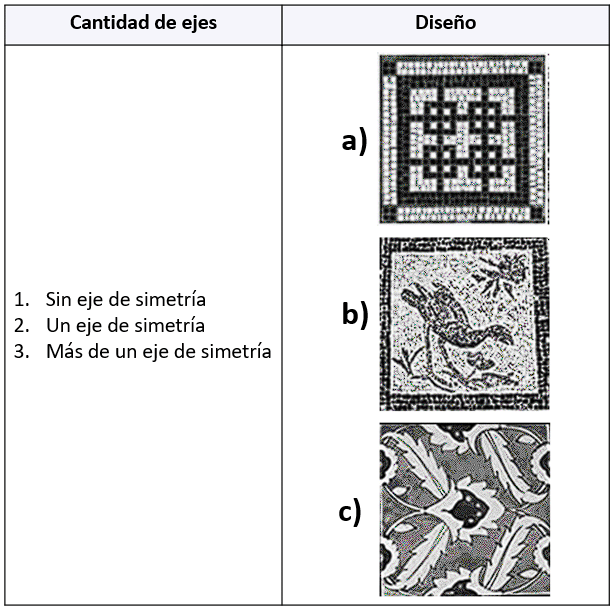
Relacione la cantidad de ejes de simetría con el diseño de mosaico que le corresponde.
- 1a, 2c, 3b
- 1b, 2c, 3a
- 1c, 2b, 3a
Solución:
Para relacionar correctamente la cantidad de ejes de simetría con la imagen respectiva, vamos a analizar cada una de las figuras en la columna derecha. Recordemos que un eje de simetría es una recta imaginaria que divide a una imagen en dos partes simétricas, es decir, se ven iguales.
Figura a.

En esta figura hay 4 ejes de simetría:
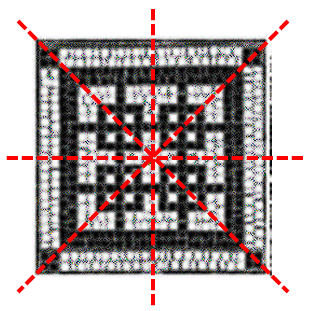
Por lo tanto: 3a.
Figura b.
En esta imagen no es posible trazar una recta que la divida en dos partes simétricas. Para este inciso: 1b. Con los datos que tenemos hasta el momento: 1b, …, 3a podemos concluir que la respuesta correcta es el inciso b).
En el inciso a), la combinación 1a es incorrecta, ya que el diseño de mosaico (a) tiene más de un eje de simetría (3). Además, la combinación 3b es incorrecta, ya que el diseño de mosaico (b) no tiene eje de simetría (1).
Por otra parte, la combinación 1c y 2c del inciso c) son incorrectas. El diseño de mosaico (c) tiene un eje de simetría (2) mientras que el diseño de mosaico (b) no tiene eje de simetría (1).
Reactivo 22
En un juego de basquetbol, el árbitro le da 2 tiros libres a un equipo para cobrar 1 falta.
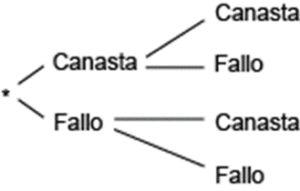
¿Qué diagrama de árbol representa correctamente las diferentes posibilidades de lo que puede ocurrir con los resultados de los tiros libres?
Solución:
Para construir el diagrama de árbol asociado a lanzar canasta dos veces seguidas, se debe considerar que en cada lanzamiento hay dos posibles resultados: fallar o hacer canasta.
En el primer lanzamiento:
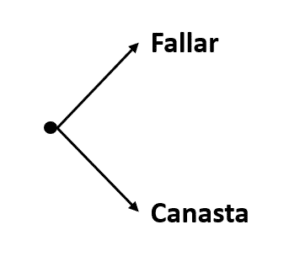
Segundo lanzamiento:
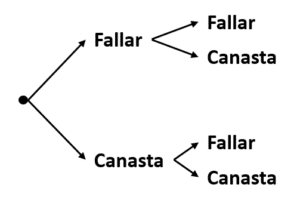
La respuesta correcta es el inciso a). En el inciso b), la primera fase tiene los resultados correctos, pero en la segunda solo escribe lo que no ha salido en la primera fase. Esto es incorrecto.
Por otro lado, en el inciso c) no se reconoce el número de resultados posibles asociado al experimento en ninguna de las fases.
Reactivo 23
El cuadro indica los salarios en pesos de una muestra de empleados de una empresa:
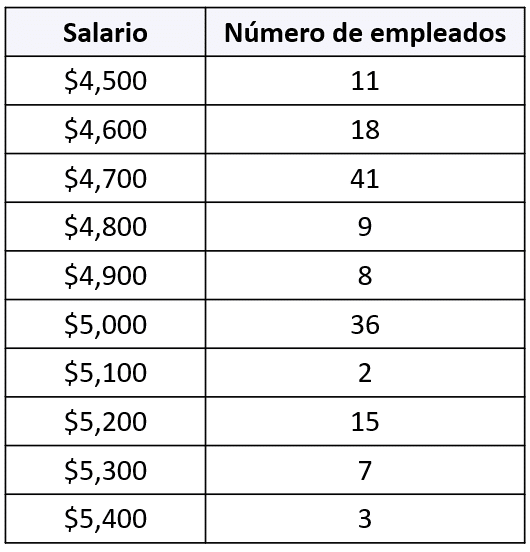
¿Cuál es el salario por debajo del cual queda 36% de los empleados?
- $4,500
- $4,700
- $5,000
Solución:
Los percentiles son 99 números denominados parámetros estadísticos de posición, que permiten dividir al conjunto de datos en 100 particiones con la misma cantidad de elementos.
Por esta razón, el percentil 36 representará el 36% de la población. Tengamos en cuenta que los salarios deben estar ordenados en forma ascendente, tal como se indica en la tabla. La frecuencia acumulada del percentil se calcula como:
{P}_{n}=\frac{k\cdot N}{100}
Donde k es el percentil en cuestión y N es el total de datos. A partir de la tabla, sabemos que en total de datos es igual a 150. Sustituyendo se obtiene:
{P}_{36}=\frac{\left(36\right)\left(150\right)}{100}=54
Ahora, buscamos en la tabla el salario cuya frecuencia acumulada sea inmediatamente mayor o igual a 54.
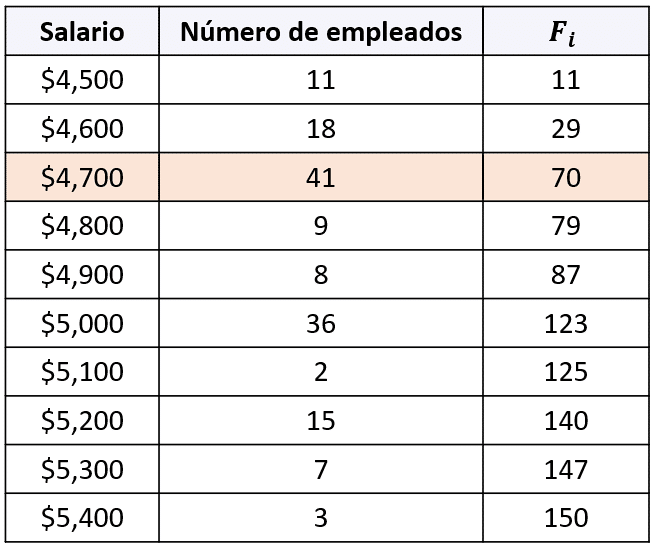
Esta frecuencia acumulada se ubica en el salario de $4,700 pesos. La respuesta correcta es el inciso b). En el inciso a), se ha aplicado mal la fórmula para el cálculo del percentil; se divide el total de datos por 100 pero no se multiplica por 36.
Si escogiste al inciso c) como respuesta correcta, probablemente consideraste que el 36% corresponde a la frecuencia, por ende, el salario es de $5,000. Lo anterior es incorrecto.
Reactivo 24
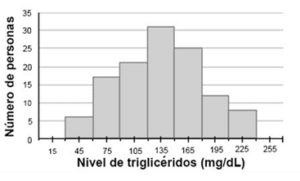
Se realizó un estudio acerca de los niveles de triglicéridos con los grupos de personas que acudieron a diversos laboratorios clínicos a realizarse una prueba de sangre. Sobre uno de los laboratorios clínicos se comentó: “Las personas en promedio tienen un nivel de triglicéridos de 135 mg/dL de sangre; sin embargo, el número de personas con los mismos niveles de triglicéridos es muy variable. Así como hay muchas con un nivel de triglicéridos alrededor de 45 mg/dL, otro tanto casi igual presenta niveles altos cercanos a 225 mg/dL”.
¿Qué gráfica representa la descripción anterior?
Solución:
Para identificar el gráfico de barras que representa al conjunto de datos, no es necesario realizar ningún cálculo, solo hay que considerar la última parte de la frase:
…el número de personas con los mismos niveles de triglicéridos es muy variable. Así como hay muchas con un nivel de triglicéridos alrededor de 45 mg/dL, otro tanto casi igual presenta niveles altos cercanos a 225 mg/dL.
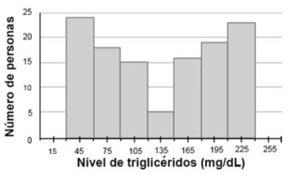
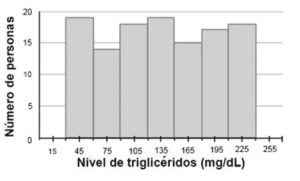
La variabilidad nos permite descartar al gráfico c), porque allí los datos se encuentran bastante cerca unos de otros. Tanto en el gráfico a) como en el b) hay variabilidad, pero solo en el b) se cumple que hay muchas con un nivel de triglicéridos alrededor de 45 mg/dL…, mientras que en el c) hay muy pocas con 45 y con 225 mg/dL.
Con el análisis anterior, concluimos que la respuesta correcta es el inciso b).
Reactivo 25
Seleccione el valor numérico que debe colocarse en el recuadro de la potencia.
La expresión {\left({\left({\left(q\right)}^{9}\right)}^{7}\right)}^{2} se puede escribir como {\left({\left(q\right)}^{9}\right)}^{\_\_} .
- 9
- 14
- 49
Solución:
En este caso, aplicamos la propiedad de los exponentes llamada potencia de una potencia, en la que multiplicamos al 2 con el 7 para simplificarlos en un solo exponente.
{\left({\left({\left(q\right)}^{9}\right)}^{7}\right)}^{2}={\left({\left(q\right)}^{9}\right)}^{14}
Sabemos que se debe aplicar entre el 7 y el 2, porque en {\left({\left(q\right)}^{9}\right)}^{\_\_} se mantiene al 9. La respuesta correcta es el inciso b).
Si seleccionaste como correcto al inciso a), has sumado el 7 con el 2 en lugar de multiplicar. Mientras que en el inciso c) se eleva la segunda potencia al 7, operación también incorrecta.
Reactivo 26
¿Qué opción es equivalente a la expresión 4(2m + n)(2m + n)?
- (4m + 2n)2
- (8m + 4n)2
- (8m + n)2
Solución:
Primero, expresamos el producto entre los binomios 2m+n como una potencia al cuadrado.
4\left(2m+n\right)\left(2m+n\right)=4{\left(2m+n\right)}^{2}
Ahora, expresamos al 4 como una potencia de base 2 y aplicamos producto de potencias de igual exponente.
4{\left(2m+n\right)}^{2}={2}^{2}{\left(2m+n\right)}^{2}={\left[2\left(2m+n\right)\right]}^{2}
Finalmente, resolvemos la distributiva,
{\left[2\left(2m+n\right)\right]}^{2}={\left(4m+2n\right)}^{2}
La respuesta correcta es el inciso a). En el inciso b) se aplica de manera incorrecta la propiedad distributiva de la multiplicación, debido a que el 4 y el binomio {\left(2m+n\right)}^{2} no tienen el mismo exponente.
Por otra parte, en el inciso c) el error puede analizarse desde 2 perspectivas. La primera, es expresar el binomio como una potencia y multiplicar el 4 solo por el primer término.
4{\left(2m+n\right)}^{2}={\left(8m+n\right)}^{2}
La segunda consta en multiplicar el 4 al inicio en ambos binomios.
4\left(2m+n\right)\left(2m+n\right)=\left(8m+n\right)\left(8m+n\right)={\left(8m+n\right)}^{2}
Reactivo 27
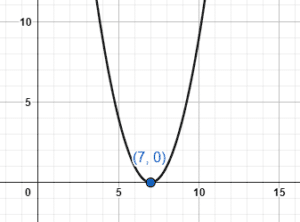
La siguiente gráfica representa a la parábola y={\left(x-8\right)}^{2} .
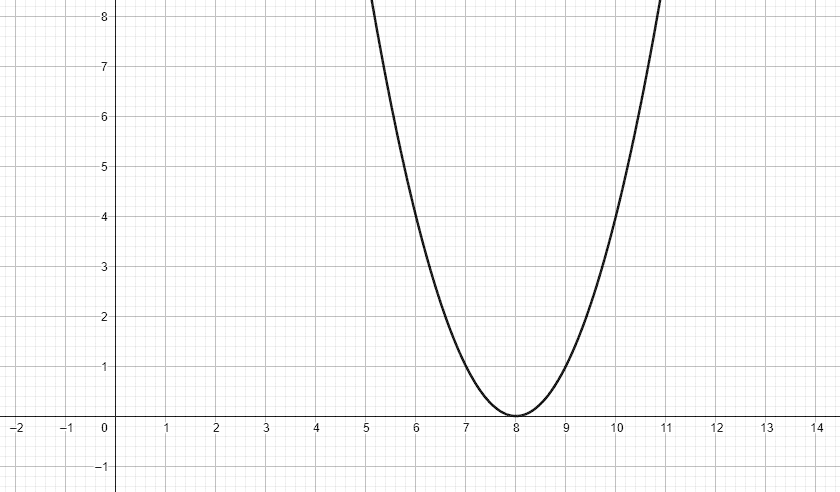
¿Cuál es la gráfica que representa a la parábola y={\left(x-8-1\right)}^{2} ?
Solución:
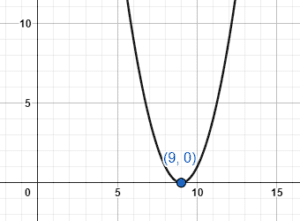
En la ecuación de la parábola se resta 1 a la coordenada horizontal del vértice, esto se traduce en un desplazamiento hacia la derecha 1 unidad de la parábola. Es decir, de encontrarse en +8, ahora se sitúa en +9.
y={\left(x-8-1\right)}^{2}={\left(x-9\right)}^{2}
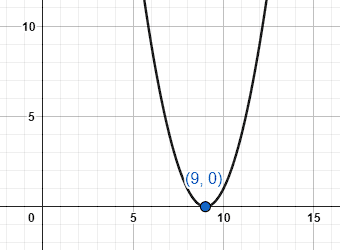
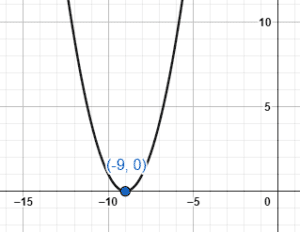
La respuesta correcta es el inciso c). En el inciso a) se identifica de manera incorrecta la transformación que sufre la gráfica. Has considerado que restar una unidad implica un movimiento horizontal del vértice 1 unidad a la izquierda sobre el eje X y esto es incorrecto.
Por otro lado, en el inciso b) has relacionado el signo de la coordenada horizontal del vértice con el signo que debería tener en el plano cartesiano, pero el signo negativo implica un desplazamiento hacia la derecha. No a la izquierda.
Reactivo 28
En la tabla se presenta información referente a tres municipios de México: el número aproximado de habitantes y el número de casos activos de covid-19 (personas enfermas) al 11 de agosto de 2020.
De acuerdo con los datos, ¿en qué municipio el número de casos activos es mayor por cada 1.000 habitantes?

- Guadalajara, Jalisco
- Naucalpan de Juárez, Estado de México
- Monclova, Coahuila
Solución:
En este caso, debemos expresar los datos proporcionados respecto a mil habitantes mediante regla de tres y luego se comparan las cantidades.
Guadalajara, Jalisco.
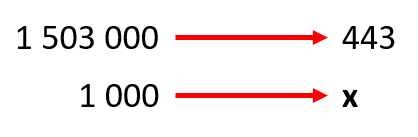
x=\frac{443}{1503000}\cdot 1000=0.295 \mathrm{c}\mathrm{a}\mathrm{s}\mathrm{o}\mathrm{s}\mathrm{ }\mathrm{c}\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{ }\mathrm{h}\mathrm{a}\mathrm{b}.
Naucalpan de Juárez, Estado de México.

x=\frac{437}{755000}\cdot 1000=0.579 \mathrm{c}\mathrm{a}\mathrm{s}\mathrm{o}\mathrm{s}\mathrm{ }\mathrm{c}\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{ }\mathrm{h}\mathrm{a}\mathrm{b}.
Monclova, Coahuila.

x=\frac{369}{245000}\cdot 1000=1.506 \mathrm{c}\mathrm{a}\mathrm{s}\mathrm{o}\mathrm{s}\mathrm{ }\mathrm{c}\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{l}\mathrm{ }\mathrm{h}\mathrm{a}\mathrm{b}.
El municipio con más casos por cada mil habitantes es Monclova, Coahuila. La respuesta correcta es el inciso c).
Reactivo 29
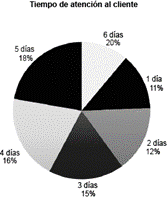
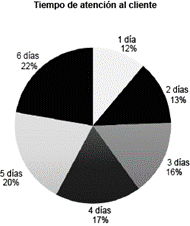
El siguiente gráfico de barras representa el número de días que esperan los clientes que llamaron a una empresa telefónica para solucionar un problema con su celular.
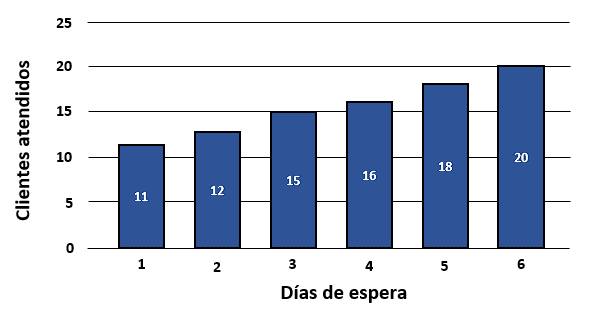
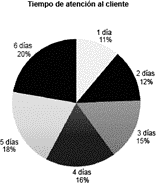
¿Cuál gráfico circular representa de manera equivalente la información?
Solución:
Debido a que los gráficos circulares están expresados en porcentajes, iniciamos convirtiendo las frecuencias del histograma a porcentaje para realizar la comparación.
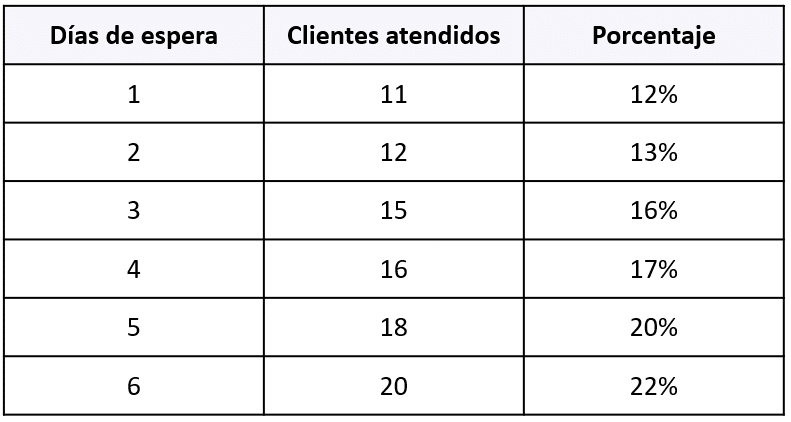
Examinando los gráficos circulares, el del inciso c) corresponde con los porcentajes calculados y cada porción del gráfico es proporcional a dicho valor porcentual. Recuerda que la fórmula para calcular porcentajes es:
\%=\frac{\mathrm{V}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{r}}{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}\cdot 100\%
Tanto en el inciso a) como en el b) se considera erróneamente que la frecuencia de los datos corresponde con el porcentaje. Por otra parte, en el inciso b) las porciones no son proporcionales a los valores porcentuales.
Reactivo 30
Al lanzar 2 dados, la probabilidad de que la suma de sus caras superiores sea 10 es _______ la probabilidad de que la suma de dichas caras sea 5.
- mayor que
- menor que
- igual a
Solución:
Para resolver el problema, iniciamos identificando los posibles resultados al lanzar dos dados.

El espacio muestral para que la suma de las caras sea 5 es 4, mientras que para sumar 10 es 3. Por lo tanto, la probabilidad de que las caras sumen 10 es menor a la probabilidad de que sumen 5.
Al lanzar 2 dados, la probabilidad de que la suma de sus caras superiores sea 10 es menor que la probabilidad de que la suma de dichas caras sea 5.
La respuesta correcta es el inciso b). Si seleccionaste como correcto al inciso a), probablemente hayas hecho la comparación entre las cantidades 10 y 5 y no entre los elementos de cada espacio muestral.
Por otra parte, el error del inciso c) consta en pensar que hay 36 posibles resultados para ambos eventos, afirmación que es incorrecta refiriéndonos a la tabla anterior.