En este post vamos a resolver la segunda parte de los reactivos de matemáticas de la guía Exani II correspondiente a la parte de pensamiento matemático. Si llegaste hasta aquí, y no sabes dónde encontrar la primera parte, abajo encontraras el link.

Este es un breve resumen del Exani II:
- Desarrollo: Ceneval
- Examen de admisión: Exani II
- Reactivos: 168
- Tipo: Opción multiple
- Duración: 4 horas y media
- Modalidades: Presencial, en línea y desde casa.
Estructura del Exani II
Antes de continuar con segunda parte de la solución de la guía en la parte de pensamiento matemático es muy importante que te quede claro la nueva estructura del Exani II.
Recuerda que el nuevo examen de admisión de Ceneval Exani II incluye las siguientes áreas:
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Tabla Estructura Exani II
Te repito que este año cambiaron el examen, aunque no es un cambio radical, ciertas áreas de la versión pasada desaparecieron y añadieron nuevos módulos a las especialidades y áreas de estudio.
Si deseas conocer en detalle todos y cada uno de los cambios del nuevo Exani II ingresa al siguiente blog post en donde te explicamos todos y cada uno de los cambios y los temas que debes estudiar.
Temario pensamiento matemático
A continuación presentamos la tabla que desglosa los 30 reactivos que componen la sección de pensamiento matemático en el Exani II.
| Subárea | Tema | Num. de reactivos |
|---|---|---|
| Comprensión de lo matemático | Conexiones | 18 |
| Estimación | ||
| Sentido matemático | ||
| Matematización | Desarrollo de usos | 12 |
| Lenguaje matemático | ||
| Resignificaciones | ||
| Total | 30 |
Algunos temas específicos son:
- Inecuaciones lineales
- Simplificación de expresiones algebraicas
- Razones trigonométricas
- Área
- Desviación estándar
- Media aritmética
- Razones y proporciones
- Interpretación gráfica de ecuaciones lineales
- Ejes de simetría
- Estimación de trayectorias
- Frecuencias
- Probabilidad clásica de eventos simples
- Leyes de los exponentes
- Porcentaje
- Unidades de medida como patrón de comparación
- Espacio muestral
- Representación gráfica de ecuaciones de segundo grado
- Comportamiento gráfico de funciones cuadráticas
- Relaciones trigonométricas
- Representación gráfica de información
- Medidas de tendencia central y de dispersión
- Polinomios
- Sistemas de ecuaciones lineales con dos y tres incógnitas
- Variación lineal tabular
- Medidas de posición (deciles, cuartiles y percentiles)
Reactivo 11: Punto medio de un segmento
¿Cuáles son las coordenadas del punto que divide en partes iguales el segmento con extremos en (1, 0) y (6, 5)?
- (2.5,2.5)
- (2.5,3.5)
- (3.5,2.5)
- (3.5,3.5)
Solución:
Las coordenadas del punto medio en el segmento de recta con extremos (1, 0) y (6, 5), son:
P_{m}\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)
Identificamos como P_{1} a (1, 0) y como P_{2} a (6, 5). Solo nos queda sustituir en la ecuación.
P_{m}\left(\frac{1+6}{2}, \frac{0+5}{2}\right)=P_{m}\left(\frac{7}{2}, \frac{5}{2}\right)=P_{m}(3.5,2.5)
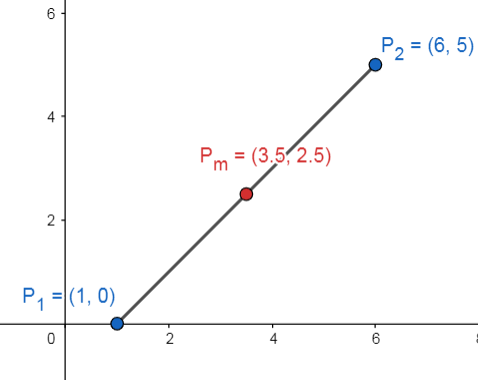
Concluimos seleccionando como respuesta correcta la opción c).
Reactivo 12: Plano cartesiano
En un plano cartesiano, ¿qué cuadrantes conecta una línea que comienza en el punto (-5, 2) y termina en el (-3, -2)?
- 1, 2
- 1, 4
- 2, 3
- 3, 4
Solución:
El problema solicita que indiquemos los cuadrantes del plano cartesiano que se conectan si trazamos una recta entre los puntos (-5, 2) y (-3, -2). Para encontrar la respuesta correcta, solo debemos identificar el cuadrante al que pertenece cada extremo.
Punto inicial: (-5, 2).
Con la coordenada en x negativa, nos deja dos posibilidades el segundo o tercer cuadrante ya que la coordenada y es positiva, podemos asegurar que el punto se encuentra en el segundo cuadrante.
Punto final: (-3, -2).
Ambas coordenadas son negativas, esto ocurre en el tercer cuadrante por tanto el extremo final está en el tercer cuadrante.
Concluimos entonces que la recta trazada entre ambos puntos une a los cuadrantes 2 y 3.
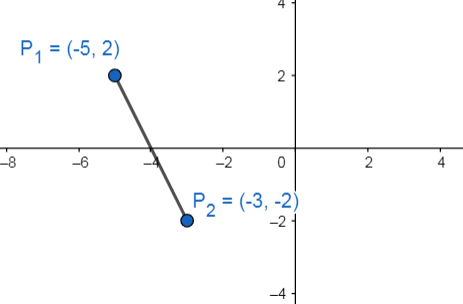
Comparando con las opciones, escogemos como respuesta correcta a la c).
Reactivo 13: Media aritmética
Calcule la media de los datos que corresponden al crecimiento de 10 niños en un mes.
3,2,5,4,0,3,0,2,1,3
- 2.3
- 2.5
- 2.8
- 3.0
Solución:
La media aritmética de un conjunto de datos desagrupados, es decir sin intervalos se obtiene al sumar todos los datos y dividir el resultado por la cantidad que se ha recolectado.
M_{e}=\frac{\sum_{1}^{n} x_{i}}{n}
Donde es la cantidad de datos y \sum_{1}^{n} x_{i} es la suma de todos los datos del experimento. Antes de sustituir en la ecuación, ordenamos las medidas de crecimiento de menor a mayor.
0,0,1,2,2,3,3,3,4,5
La cantidad de datos en este caso es 10, n=10 y la suma de las medidas es:
\sum_{1}^{n} x_{i}=0+0+1+2+2+3+3+3+4+5=23
Sustituimos ambos resultados en la ecuación de la media aritmética.
M_{e}=\frac{23}{10}=2.3
La media de crecimiento de los 10 niños en un mes fue de 2.3. Comparando con las opciones del problema, escogemos como respuesta correcta a la a).
Reactivo 14: Histograma de frecuencias
La gráfica presenta la frecuencia absoluta de número de hijos en una muestra de 22 familias. ¿Cuántas tienen más de 1 hijo?
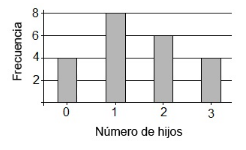
- 4
- 6
- 10
- 18
Solución:
Un histograma de frecuencias es un mecanismo de estudio en estadística que permite representar, de forma gráfica la cantidad de veces que se repite un conjunto de eventos. En este caso, representa cuántas familias tienen de 0 a 3 hijos.
El problema solicita que indiquemos cuántas familias tienen más de un hijo, es decir cuántas tienen 2 y 3 hijos. A partir del diagrama, sabemos que 6 familias tienen 2 hijos y que 4 tienen 3 hijos; dando un total de 10 familias con más de 1 hijo.
Comparando con las opciones del problema, seleccionamos como respuesta correcta al inciso c).
Reactivo 15: Media aritmética
Para conservar su beca, Mariana debe mantener un 85 de promedio en sus 4 exámenes. Si en los 3 primeros obtuvo 62, 88 y 96, ¿cuál calificación debe obtener en el cuarto examen?
- 82
- 83
- 88
- 94
Solución:
Sabemos que el promedio académico se calcula como la media aritmética de las calificaciones obtenidas en un periodo académico:
P=\frac{\sum_{1}^{n} x_{i}}{n}
En este caso, el promedio es P=85 , la suma de las calificaciones es \sum_{1}^{n} x_{i}=62+88+96+x y la cantidad de exámenes es n=4 , sustituimos en la ecuación y despejamos a x como la calificación del cuarto examen.
85=\frac{62+88+96+x}{4} \rightarrow 4 \cdot 85=62+88+96+x
x=4 \cdot 85-62-88-96=94
Mariana debe obtener un 94 en su cuarto examen para mantener su promedio de 85.
Comparando con las opciones, la respuesta correcta es la d).
Reactivo 16: Probabilidad
Al lanzar un dado, ¿cuál es la probabilidad de que salga el 5?
- \frac{1}{6}
- \frac{5}{6}
- 1
- 5
Solución:
La probabilidad de un suceso A se calcula como el número de casos favorables al suceso sobre el número total de casos posibles. En un dado común (sin que esté trucado) de 6 caras, existen 6 posibles resultados al lanzarlo y solo 1 de esas posibilidades es 5.
Es decir, solo hay un caso favorable para que salga 5. La probabilidad la calculamos como:
P(5)=\frac{1}{6}
Comparando con las opciones, seleccionamos como respuesta correcta al inciso a).
Reactivo 17: Producto de monomios
¿Cuál es el resultado de la multiplicación de monomios?
(3 x y)\left(4 x^{2} y^{3}\right)
- 7 x^{2} y^{4}
- 7 x^{3} y^{4}
- 12 x^{2} y^{3}
- 12 x^{3} y^{4}
Solución:
Para multiplicar dos monomios, se agrupan los factores numéricos y luego los factores literales con la misma base; luego se realiza el producto de las cantidades numéricas y se aplica suma o resta de exponentes a los literales de igual base.
En nuestro caso, los factores numéricos son 3 y 4, mientras que los literales son x \text { у } y .
\begin{aligned} (3 x y)\left(4 x^{2} y^{3}\right) &=(3 \cdot 4)\left(x \cdot x^{2}\right)\left(y \cdot y^{3}\right) \\ &=12 x^{3} y^{4} \end{aligned}
Comparando con los incisos, seleccionamos como respuesta correcta al d).
Reactivo 18: Punto medio
Dado el segmento de recta AB, el punto medio está dado por la expresión:
- \frac{A+B}{2}
- \frac{A-B}{2}
- \frac{-A+B}{2}
- \frac{-(A+B)}{2}
Solución:
En este caso, los extremos del segmento son los puntos A \text { у } B de los que supondremos tienen coordenadas en el plano cartesiano, es decir R^{2} . Si cada punto tiene coordenadas A\left(a_{x}, a_{y}\right) \text { у } B\left(b_{x}, b_{y}\right) , las coordenadas del punto medio son:
P_{m}=\left(\frac{a_{x}+b_{x}}{2}, \frac{a_{y}+b_{y}}{2}\right)
Si separamos las fracciones nos queda:
P_{m}=\left(\frac{a_{x}}{2}+\frac{b_{x}}{2}, \frac{a_{y}}{2}+\frac{b_{y}}{2}\right)
Descomponemos el punto como la suma de dos puntos.
=\left(\frac{a_{x}}{2}+\frac{b_{x}}{2}, \frac{a_{y}}{2}+\frac{b_{y}}{2}\right)=\left(\frac{a_{x}}{2}, \frac{a_{y}}{2}\right)+\left(\frac{b_{x}}{2}, \frac{b_{y}}{2}\right)
Extraemos \frac{1}{2} factor común.
=\frac{1}{2}\left(a_{x}, a_{y}\right)+\frac{1}{2}\left(b_{x}, b_{y}\right)
Sustituimos las denominaciones de cada punto y aplicamos la suma de fracciones de igual base.
P_{m}=\frac{A+B}{2}
A partir de las opciones del problema, seleccionamos como respuesta correcta la a).
Reactivo 19: Producto de potencias
El resultado de la expresión 3^{3} 4^{2} es…
- 72
- 432
- 16,807
- 248,832
Solución:
Primero resolvemos cada potencia por individual y culminamos con el producto de ambos resultados. El 3 elevado al cubo es 3^{3}=3 \cdot 3 \cdot 3=27 y el cuadrado de 4 es 4^{2}=4 \cdot 4=16 .
3^{3} 4^{2}=27 \cdot 16
Por último, efectuamos el producto de 27 y 16.
3^{3} 4^{2}=27 \cdot 16=432
Escogemos como respuesta correcta a la opción b).
Reactivo 20: Operaciones aritméticas
Es el resultado de la expresión
8(-3-2+5)+5(-8+9-3)-[6(-9)]
- 44
- 52
- 60
- 64
Solución:
El orden de las operaciones es:
- Interior de corchetes
- Interior de paréntesis
- Productos y cocientes
- Sumas y restas
Resolvemos el producto dentro de los corchetes.
8(-3-2+5)+5(-8+9-3)-[6(-9)]=8(-3-2+5)+5(-8+9-3)-(-54)
Ahora, vamos con el interior de los paréntesis.
8(-3-2+5)+5(-8+9-3)-(-54)=8(0)+5(-2)-(-54)
Deshacemos los paréntesis y resolvemos los productos pendientes.
8(0)+5(-2)-(-54)=0-10+54
Culminamos con las sumas y restas.
-10+54=44
Escogemos como respuesta correcta a la opción a).


