¡Nos vemos de nuevo, aspirante! Vamos con la solución de la Guía Interactiva de EXANI II, en el módulo de Física, en esta ocasión resolveremos desde el reactivo 1 hasta el 12.

Física es una asignatura con gran extensión teórica, repasa bien los conceptos antes de pasar a los ejercicios. Esto te dará una mejor perspectiva a la hora de pensar una estrategia y llegar a la solución.
Estructura del EXANI II
El examen de ingreso EXANI II se compone de dos grandes áreas, cada una con la misma importancia en la nota final:
- Habilidades y conocimientos
- Los módulos específicos.
Añadi
También existe una prueba diagnóstico de inglés que aplican algunas universidades y cuyo resultado no repercute en la nota final.
Examen de habilidades y conocimientos
La primera parte del EXANI II 2023 es igual para todas las carreras y se compone de 90 reactivos: 60 de Español y 30 de Matemáticas.
La siguiente tabla resume la distribución de los reactivos en la prueba de ingreso EXANI II:
Estructura del examen y la guía del EXANI II
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Conocimientos específicos
Esta segunda parte posee un total de 15 módulos en los que se encuentra física. Todos los estudiantes deben responder 2 módulos en esta segunda parte, los cuales varían de acuerdo con la carrera.
Es necesario que revises la convocatoria de tu universidad para conocer qué módulos debes estudiar.
Módulos de los conocimientos específicos
| 1. Administración | 9. Física |
| 2. Aritmética | 10. Historia |
| 3. Biología | 11. Literatura |
| 4. Cálculo diferencial e integral | 12. Matemáticas financieras |
| 5. Ciencias de la Salud | 13. Premedicina |
| 6. Derecho | 14. Probabilidad y estadística |
| 7. Economía | 15. Química |
| 8. Filosofía | 16. Psicología |
Temario Física EXANI II
En la siguiente tabla te mostramos la distribución de los 24 reactivos de física, junto a los temas que van para el examen.
| Subárea | Reactivos |
|---|---|
| Mecánica | 10 |
| Óptica, ondas y electromagnetismo | 14 |
| Total | 24 |
Subárea: Mecánica
- Sistemas de fuerzas coplanares concurrentes y distribuidos
- Elementos que intervienen en el movimiento circular uniforme
- Cálculo de fuerza centrípeta
- Variables relacionadas con el trabajo rotacional y la energía cinética rotacional
- Conservación del momento angular
- Ley de la conservación de la cantidad de movimiento
- Tipos de choque y variables relacionadas
Subárea: Óptica, ondas y electromagnetismo
- Sistemas de objetos que interactúan a través de sus campos magnéticos
- Generación de fuerza magnética
- Sistemas de fuerzas entre corrientes
- Sistemas conductores que generan campos magnéticos
- Tipos y variables que intervienen en el movimiento armónico simple
- Clasificación, componentes y representación gráfica de ondas
- Aplicación tecnológica de fenómenos ondulatorios
- Tipos de lente
- Características y parámetros que intervienen en los fenómenos ópticos
Añad
Recomendaciones para resolver la guía interactiva
Te dejo algunos trucos para sacarle el máximo provecho a la guía EXANI II 2023 que puedes tener en cuenta a la hora de estudiar:
- Elimina las distracciones. Ve a un sitio en el que te sientas cómodo o cómoda, coloca tu teléfono en modo avión y mantén cerca de ti lapiceros, borrador y libretas.
- No te enfoques en el resultado, sino en el procedimiento. Coloca toda tu atención en analizar y desglosar los problemas para identificar las herramientas que debes usar. Una buena estrategia conlleva a buenos resultados.
- Lleva el tiempo mientras resuelves la guía. Mide el tiempo durante cada sesión de estudios, buscando acortar el tiempo lo más que puedas antes del examen.
- Si un reactivo parece demasiado difícil, ve al siguiente. Evita caer en frustración mientras estudias, mantener el foco y meditar esos ejercicios difíciles, te permitirán desarrollar capacidades analíticas sólidas.
Reactivo 1
Seleccione el ejemplo en el que se describe un movimiento armónico simple.
- El aleteo de un ave al emprender el vuelo
- La cuerda de una guitarra al ser rasgada
- Los pasos al descender de una pendiente
Solución:
Un movimiento armónico simple, es aquel que completa trayectorias cerradas forma periódica, en intervalos de tiempo constante. Un ejemplo clásico de MAS es el péndulo simple.
Con esta definición en mente, podemos analizar cada una de las situaciones en los incisos para determinar cuál de ellas describe un MAS.
El aleteo de un ave al emprender el vuelo.
Aunque un ave necesita mover sus alas hacia arriba y hacia abajo repetidamente, durante el ascenso del vuelo no lo hace de forma periódica y tampoco con la misma intensidad.
Además de lograr el impulso hacia arriba, el ave necesita estabilizar su posición y para ello debe corregir constantemente la velocidad y amplitud de los aleteos, provocando que no sea un MAS. Descartamos el inciso a).
La cuerda de una guitarra al ser rasgada.
Suponiendo que la cuerda es ideal y despreciando el rozamiento con el aire, cuando un guitarrista rasga la cuerda de una guitarra provoca la propagación de una onda a lo largo de la misma, que la hace vibrar a una frecuencia que depende de las características físicas de la cuerda.
Debido a que tanto la frecuencia como la amplitud se mantienen en la cuerda ideal, podemos concluir que se trata de un MAS. La respuesta correcta es el inciso b).
Los pasos al descender de una pendiente.
Similar a lo que ocurre con el ascenso del ave, cuando bajamos por una pendiente nuestros pasos buscan estabilizar el centro de masas durante recorrido mientras transitamos, evitando ir a una velocidad que posteriormente nos haga caer. Por esta razón, los pasos no ocurren a la misma frecuencia, siendo algunos más cortos que otros. Esta no puede ser la respuesta correcta.
Reactivo 2
Las lentes divergentes generan imágenes de…
- menor tamaño, virtuales y no invertidas
- mayor tamaño, reales e invertidas
- igual tamaño, reales e invertidas
Solución:
En los lentes divergentes, la imagen siempre es virtual, derecha y de menor tamaño, sin importar la distancia entre el objeto y la lente.
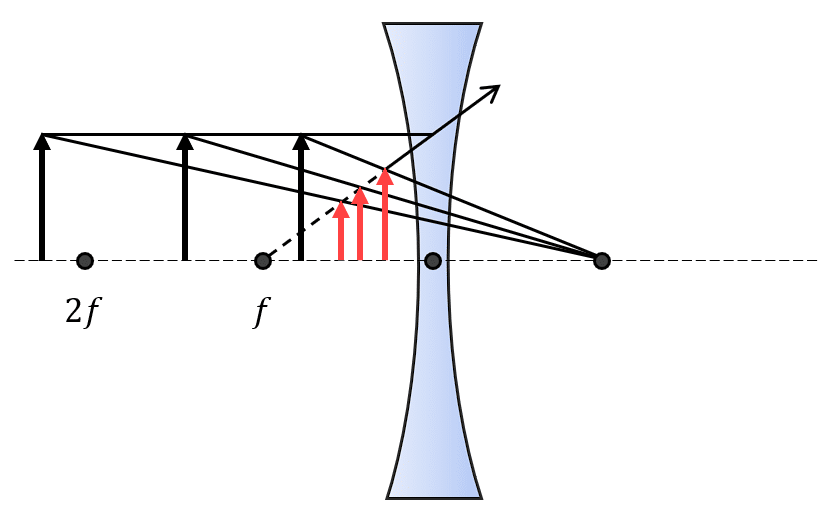
La respuesta correcta es el inciso a). El error en el inciso b) ocurre al confundir los distintos casos de las lentes convergentes con la formación de imágenes en lentes divergentes, ninguna lente divergente creará imágenes reales.
Por otro lado, la opción c) describe el caso de la imagen formada por una lente convergente al situar el objeto a dos veces la distancia focal.
Reactivo 3
Un objeto colocado en la orilla de un disco tiene una cantidad de movimiento angular de 16 \mathrm{k}\mathrm{g}\cdot \frac{{\mathrm{m}}^{2}}{\mathrm{s}} y gira a 20\cdot \frac{\mathrm{r}\mathrm{a}\mathrm{d}}{\mathrm{s}} . Calcule la inercia rotacional.
- 0.04 {\mathrm{k}\mathrm{g}\cdot \mathrm{m}}^{2}
- 0.8 {\mathrm{k}\mathrm{g}\cdot \mathrm{m}}^{2}
- 1.25 {\mathrm{k}\mathrm{g}\cdot \mathrm{m}}^{2}
Solución:
A partir de los datos suministrados por el enunciado, la inercia rotacional del objeto se calcula mediante la siguiente ecuación:
L=I\omega
Despejando la inercia rotacional nos queda:
I=\frac{L}{\omega }=\frac{16 \mathrm{k}\mathrm{g}\cdot \frac{{\mathrm{m}}^{2}}{\mathrm{s}}}{20\cdot \frac{\mathrm{r}\mathrm{a}\mathrm{d}}{\mathrm{s}}}=0.8 \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{2}
La inercia rotacional del objeto es igual a 0.8 \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^{2} .
La respuesta correcta es el inciso b). En la opción a) se eleva al cuadrado a velocidad angular, mientras que en el inciso c) se despeja de forma incorrecta a la variable.
Reactivo 4
¿Qué dispositivo emplea ondas electromagnéticas para su funcionamiento?
- Apuntador láser
- Motor eléctrico
- Bocina
Solución:
Las ondas electromagnéticas son perturbaciones simultáneas de los campos eléctricos y magnéticos que se propagan a lo largo de una región del espacio. Las ondas electromagnéticas se clasifican por su longitud de onda, encontrándose la luz visible en el rango de 400 a 700 nanómetros
Los láseres son un fenómeno electromagnético de la luz visible producido de manera artificial, en el que se logra emitir un haz de luz estrecho y cuyas componentes poseen la misma longitud de onda. Teniendo en cuenta lo anterior, concluimos que la respuesta correcta es el inciso a).
Tanto el inciso b) como el c) enuncian dos máquinas eléctricas, las cuales utilizan campos eléctricos y magnéticos para convertir energía eléctrica en energía mecánica.
Reactivo 5
Calcule la distancia que separa a dos conductores rectos y paralelos que miden 0.5 m de largo, por cada uno de los cuales circula una corriente de 7 A en el mismo sentido y que resienten una fuerza de atracción de 2.25\times {10}^{-4} \mathrm{N} .
Considere \pi =3.14 y el valor de la permeabilidad magnética como {\mu }_{0}=4\pi \times {10}^{-7}\frac{\mathrm{T}\mathrm{m}}{\mathrm{A}} .
- 0.003 m
- 0.022 m
- 0.087 m
Solución:
Para resolver el problema, empleamos la fórmula para calcular el módulo de la fuerza entre dos conductores finitos que transportan corriente eléctrica:
{F}_{12}=\frac{{\mu }_{o}L{I}_{1}{I}_{2}}{2\pi r}
Donde {I}_{1} e {I}_{2} son las corrientes, r es la distancia entre los conductores y {\mu }_{o} es la constante de permeabilidad magnética del vacío. Despejamos la distancia.
r=\frac{{\mu }_{o}L{I}_{1}{I}_{2}}{2\pi {F}_{12}}
Sustituimos los valores suministrados.
r=\frac{\left(4\pi \times {10}^{-7}\right)\left(0.5\right)\left(7\right)\left(7\right)}{2\pi \left(2.25\times {10}^{-4}\right)}=0.022 \mathrm{m}
La distancia entre los conductores portadores de corriente se encuentra a una distancia de 0.022 metros. La respuesta correcta es el inciso b). El error del inciso a) es que no se incluyó la magnitud de las corrientes en el cálculo.
En el c), ocurre un mal despeje de la ecuación, resultando en r=\frac{{\mu }_{0}{I}_{1}{I}_{2}}{2\pi LF} ; la longitud de los cables queda en el denominador.
Añadido
Reactivo 6
Determine la magnitud de la fuerza magnética sobre una partícula cargada con 4 \mu C y que se mueve a una velocidad perpendicular de 1500 \mathrm{m}/\mathrm{s} respecto al campo magnético de 0.12 \mathrm{T} .
- 4.8\times {10}^{-7} \mathrm{N}
- 7.2\times {10}^{-4} \mathrm{N}
- 7.2\times {10}^{-1} \mathrm{N}
Solución:
Para resolver el problema, se utiliza la ecuación de fuerza sobre una partícula en movimiento:
F=q\cdot B\cdot v
Donde q es la magnitud de la carga eléctrica, B es la magnitud del campo y v es la magnitud de la velocidad de la carga dentro del campo. Sustituimos los valores dados:
F=\left(4\times {10}^{-6}\right)\left(0.12\right)\left(1500\right)=7.2\times {10}^{-4} \mathrm{N}
La magnitud de la fuerza que experimenta la carga es de 7.2\times {10}^{-4} \mathrm{N} .
Como dato extra, cuando una carga eléctrica se desplaza dentro de un campo magnético, dicha fuerza provoca que la partícula describa una trayectoria helicoidal. La respuesta correcta es el inciso b).
En el inciso a) no se considera el valor de la velocidad, mientras que en el inciso c) no se ha considerado de forma correcta el prefijo micro, en lugar de {10}^{-6} se ha colocado {10}^{-3} .
Reactivo 7
Sobre una superficie horizontal 2 esferas sólidas se deslizan sin fricción, de forma colineal. La primera se desplaza hacia la derecha a 10 \mathrm{m}/\mathrm{s} y su masa es de {m}_{1}=5 \mathrm{k}\mathrm{g} . La segunda se desplaza hacia la izquierda a 5 \mathrm{m}/\mathrm{s} y su masa es de {m}_{2}=5 \mathrm{k}\mathrm{g} . Si al colisionar ambas esferas se mantienen unidas, ¿cuál es la velocidad final después del choque?
Considere el movimiento a la derecha como positivo y a la izquierda como negativo.
- 2.5 m/s
- 7.5 m/s
- 15 m/s
Solución:
Realizamos una representación gráfica de la situación. La velocidad de la masa 1 es positiva porque apunta hacia la derecha, mientras que para la segunda es negativa porque apunta hacia la derecha.
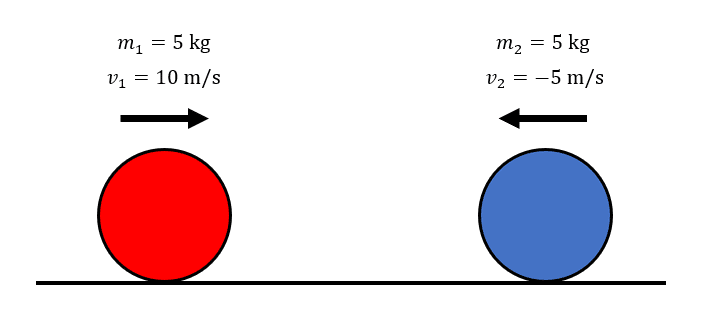
Debido a que la colisión es inelástica, los cuerpos se mantienen unidos luego del choque. Para calcular la velocidad final del conjunto, se utiliza el principio de conservación del momento lineal.
{p}_{1}={p}_{2}
El momento lineal es una cantidad vectorial, pero como el análisis es unidimensional, podemos prescindir de los vectores siempre y cuando las cantidades se escriben con el signo correspondiente. Para el instante antes del choque se tiene:
{p}_{1}={v}_{1}{m}_{1}+{v}_{2}{m}_{2}
Después del choque:
{p}_{2}={v}_{3}\left({m}_{1}+{m}_{2}\right)
Sustituimos y despejamos a la velocidad {v}_{3} de las esferas unidas.
{v}_{1}{m}_{1}+{v}_{2}{m}_{2}={v}_{3}\left({m}_{1}+{m}_{2}\right)
{v}_{3}=\frac{{v}_{1}{m}_{1}+{v}_{2}{m}_{2}}{{m}_{1}+{m}_{2}}
Finalmente, evaluamos la expresión:
{v}_{3}=\frac{\left(10\right)\left(5\right)+\left(-5\right)\left(5\right)}{5+5}=\frac{50-25}{10}=2.5 \mathrm{m}/\mathrm{s}
La velocidad de las dos esferas luego del choque es de 2.5 metros por segundo.
La respuesta correcta es el inciso a). El error del inciso b) es que no se toma en cuenta el sentido de la velocidad para la esfera 2, mientras que para el c) el despeje de la velocidad {v}_{3} es incorrecto:
{v}_{f}={m}_{1}{v}_{1i}+{m}_{2}{v}_{2i}-\left({m}_{1}+{m}_{2}\right)
Reactivo 8
Al observar un haz de luz que penetra un lago en total calma, pareciera como si el haz se doblara al entrar al agua, desviándose con un cierto ángulo de su trayectoria original.
¿Qué característica define a este fenómeno de la luz?
- Refracción
- Difracción
- Reflexión
Solución:
Este fenómeno se denomina refracción de la luz y ocurre debido al cambio de velocidad que experimenta la luz al pasar de un medio (el aire) hacia otro (el agua del lago). La respuesta correcta es el inciso a).
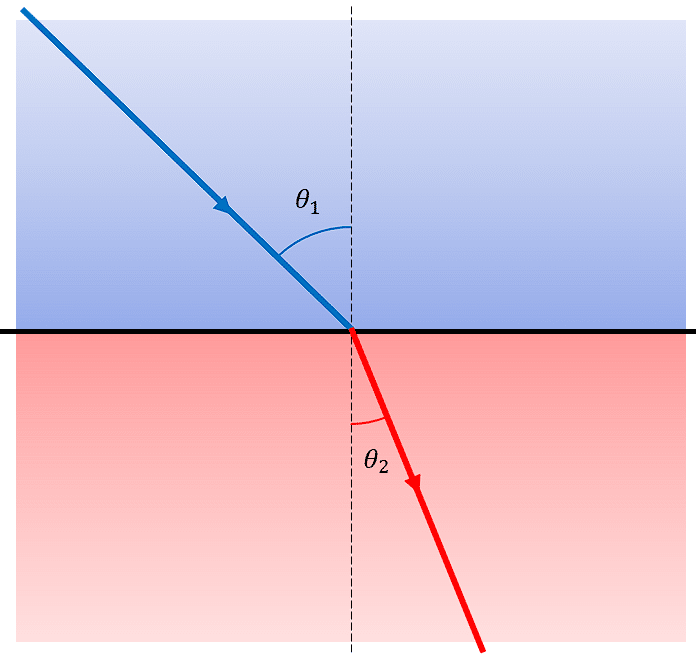
En la opción b) se indica la difracción, fenómeno que responde a la distorsión que sufre la luz al atravesar una rendija cuyo tamaño es comparable con la longitud de onda del haz.
La opción c) indica el fenómeno de reflexión, fenómeno que ocurre cuando un haz de luz interactúa con la superficie de un objeto, reflejándose hacia el medio original.
Reactivo 9
Se coloca un objeto a 4 cm de una lente divergente cuya distancia focal es de 20 cm.
Calcule la distancia a la que se formará la imagen.
- -5 cm
- -3.33 cm
- -0.3 cm
Solución:
Para resolver el problema, debemos emplear la ecuación de las lentes:
\frac{1}{f}=\frac{1}{o}+\frac{1}{i}
La distancia de la imagen es i . Despejamos:
\frac{1}{i}=\frac{1}{f}-\frac{1}{o}\to \frac{1}{i}=\frac{o-f}{of}
i=\frac{of}{o-f}
Para lentes divergentes, la distancia focal f se sustituye negativa.
i=\frac{\left(-20\right)\left(4\right)}{\left(4\right)-\left(-20\right)}=-3.33 \mathrm{c}\mathrm{m}
La imagen se encuentra a -3.33 cm del eje focal. El signo negativo indica que la imagen es virtual.
La respuesta correcta es el inciso b). En el inciso a) y en el c) se comete error en el despeje de la ecuación. El primero es con el signo de los términos y el segundo al dividir fracciones.
Reactivo 10
Calcule la longitud de la onda electromagnética que se propaga a partir de una antena que emite una frecuencia de 6 000 Hz.
Considere c=3\times {10}^{8} \mathrm{m}/\mathrm{s} .
- 2\times {10}^{-5} m
- 5\times {10}^{4} m
- 1.8\times {10}^{12} m
Solución:
Para obtener la longitud de onda, empleamos la ecuación:
\lambda =\frac{v}{f}
Donde v es la velocidad de propagación y f es la frecuencia de la onda. Sustituimos:
\lambda =\frac{3\times {10}^{8}}{6000}=5\times {10}^{4} \mathrm{m}
Seleccionamos como respuesta correcta al inciso b). En la opción a) se sustituyen al revés la frecuencia y la velocidad, mientras que en el c) se calcula el producto y no el cociente de la velocidad y la frecuencia.
Reactivo 11
Identifique el vector que corresponde a la velocidad tangencial del martillo que se muestra en la imagen.
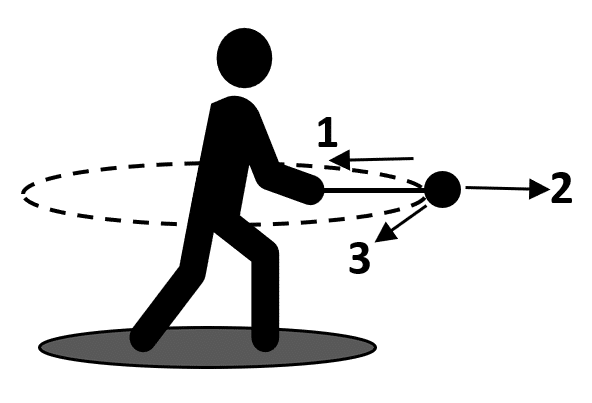
- 1
- 2
- 3
Solución:
En el movimiento circular, el vector velocidad tangencial es aquel perpendicular al radio de la trayectoria y que apunta en el sentido de rotación. Examinando la figura, el vector velocidad tangencial es el 3.
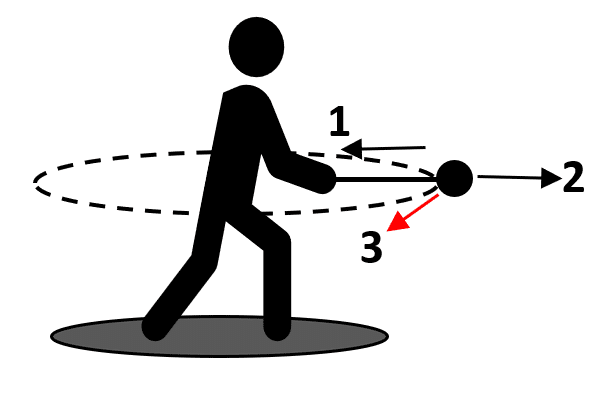
Por lo tanto, la respuesta correcta es el inciso c). Los otros dos vectores 1 y 2, son la aceleración centrípeta y centrífuga respectivamente.
Reactivo 12
Calcule la magnitud de la inducción magnética B de una bobina helicoidal con 8.000 vueltas de 0.01 m de longitud y una corriente de 0.2 A.
Considere \pi =3.14 y {\mu }_{0}=4\pi \times {10}^{-7} \frac{\mathrm{T}\mathrm{m}}{A} .
- 5\times {10}^{-4} \mathrm{T}
- 1\times {10}^{-1} \mathrm{T}
- 2\times {10}^{-1} \mathrm{T}
Solución:
Para calcular la magnitud del campo magnético producido por la bobina, se utiliza la siguiente ecuación:
B=\frac{{\mu }_{o}Ni}{r}
Donde i es la intensidad de la corriente, N es la cantidad de vueltas, r es el radio de la bobina y {\mu }_{o} es la constante de permeabilidad magnética. Sustituyendo nos queda:
B=\frac{\left(4\pi \times {10}^{-7}\right)\left(8000\right)\left(0.2\right)}{0.01}=0.2 \mathrm{T}=2\times {10}^{-1} \mathrm{T}
La respuesta correcta es el inciso c). En el inciso a) se sustituye la longitud y la corriente al revés, mientras que en el inciso b) se utiliza la fórmula para una bobina no helicoidal \frac{{\mu }_{o}Ni}{2r} .

