¡Continuamos, aspirante! Vamos por la segunda y última parte de la guía interactiva del EXANI II resuelta, correspondiente a Cálculo Diferencial e Integral, desde el reactivo 13 hasta el 24.

Recuerda medir el tiempo que tardas en resolver las guías e intenta mejorarlos con los trucos que te dejamos a continuación.
Estructura del Exani II
El Exani consta de 168 reactivos, dividiéndose en diferentes módulos que evalúan un área diferente. Algunos de estos se enfocan en conocimientos generales, mientras que otros se enfocan en conocimientos específicos que varían según la carrra a la que apliques.
Para conocer a detall la estructura de la pruba y cuántas preguntras vienen en cada parte, dale un vistazo a esta tabla:
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Reactivos Resueltos
Continúa leyendo para ver la resolución de la segunda parte de nuestra guía interactiva con reactivos de cálculo diferencial e integral.
Reactivo 13
Calcule la integral de la función exponencial.
\int {5}^{x}dx
- {5}^{x}+C
- \frac{{5}^{x}}{5}+C
- \frac{{5}^{x}}{\mathrm{ln}5}+C
Solución:
Esta integral es inmediata y se resuelve con la fórmula para una función exponencial de base a .
\int {a}^{x}dx=\frac{{a}^{x}}{\mathrm{ln}a}+C
En este caso a=5 , por lo tanto:
\int {5}^{x}dx=\frac{{5}^{x}}{\mathrm{ln}5}+C
La respuesta correcta es el inciso c). El error del inciso a) consiste en confundir la fórmula de integración con la de una exponencial base e . Por otro lado, en el inciso b) no se aplica el logaritmo natural a la base de la potencia.
Reactivo 14
Elija la derivada de la función trigonométrica.
f\left(x\right)=3\mathrm{tan}x
- 3{\mathrm{sec}}^{2}x
- {\mathrm{sec}}^{2}x
- 3\mathrm{sec}x\mathrm{tan}x
Solución:
Primero identificamos la fórmula para derivar a la tangente de x .
{\left(\mathrm{tan}x\right)}^{\text{'}}={\mathrm{sec}}^{2}x
Derivando la función y aplicando la propiedad de la derivada de una constante por una función nos queda:
{f}^{\text{'}}\left(x\right)={\left(3\mathrm{tan}x\right)}^{\text{'}}=3{\left(\mathrm{tan}x\right)}^{\text{'}}=3{\mathrm{sec}}^{2}x
La respuesta correcta es el inciso a). El error en el inciso b), es que se omite la constante; mientras que en el inciso c) se calcula la derivada de la secante, no la de tangente.
Reactivo 15
Identifique la integral de la función \int x\sqrt{x+1}dx a partir de la integración por partes.
- \frac{x}{2\sqrt{x+1}}-\sqrt{x+1}+C
- \frac{2}{3}x\sqrt{{\left(x+1\right)}^{3}}-\frac{4}{15}\sqrt{{\left(x+1\right)}^{5}}+C
- \frac{2}{3}x\sqrt{{\left(x+1\right)}^{3}}+\frac{4}{15}\sqrt{{\left(x+1\right)}^{5}}+C
Solución:
Como en toda integral por partes, debemos identificar quién será u y quien dv . Normalmente u es una función que forma parte del integrando y que, al derivarla, se convierte en una función más simple.
Por otra parte, dv es la otra función y se busca que al menos mantenga la misma estructura. En la integral del enunciado, u=x ya que al derivar esta se convierte en 1. La fórmula de integración por partes es:
\int udv=uv-\int vdu
Seleccionando las variables:
u=x\to du=dx
dv=\sqrt{x+1}dx\to v=\int \sqrt{x+1}dx
Esta integral se resuelve con la fórmula para una potencia, gracias a que \sqrt{x+1}={\left(x+1\right)}^{1/2} y el diferencial de x+1 es el mismo que para x , es decir: dx .
Lo anterior es un truco que puedes aplicar si ya has practicado integrales. Si no es evidente para ti, mediante sustitución obtendrás el mismo resultado.
v=\int {\left(x+1\right)}^{1/2}dx=\frac{2}{3}{\left(x+1\right)}^{\frac{3}{2}}
Se sustituye todo en la fórmula de integración por partes.
\int x\sqrt{x+1}dx=\frac{2}{3}x{\left(x+1\right)}^{\frac{3}{2}}-\frac{2}{3}\int {\left(x+1\right)}^{\frac{3}{2}}dx
Esta última integral es inmediata y se resuelve con el enfoque antes mencionado.
{I}_{2}=\frac{2}{3}\int {\left(x+1\right)}^{\frac{3}{2}}dx=\frac{2}{3}\cdot \frac{2}{5}{\left(x+1\right)}^{\frac{5}{2}}+C=\frac{4}{15}{\left(x+1\right)}^{\frac{5}{2}}+C
Sustituyendo en la fórmula de por partes nos queda:
I=\frac{2}{3}x{\left(x+1\right)}^{\frac{3}{2}}-\frac{4}{15}{\left(x+1\right)}^{\frac{5}{2}}+C
Expresamos las potencias fraccionarias como raíces.
I=\frac{2}{3}x\sqrt{{\left(x+1\right)}^{3}}-\frac{4}{15}\sqrt{{\left(x+1\right)}^{5}}+C
Finalmente:
\int x\sqrt{x+1}dx=\frac{2}{3}x\sqrt{{\left(x+1\right)}^{3}}-\frac{4}{15}\sqrt{{\left(x+1\right)}^{5}}+C
La respuesta correcta es el inciso b). El error del inciso a) se debe a que se derivan todos los elementos de la fórmula por partes, recuerda que se deriva u y se integra dv . En el inciso c), el error ocurre al sustituir la segunda integral, se omite el signo menos fuera de la integral.
Reactivo 16
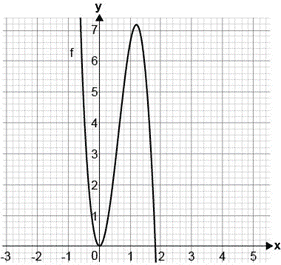
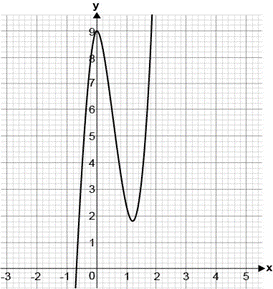
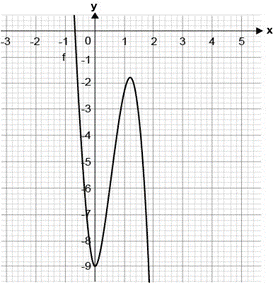
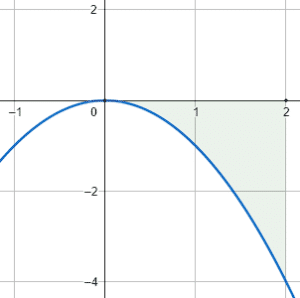
Elija la gráfica en la que se muestra que la derivada de la función cambia exactamente 2 veces de signo y en la que una de sus raíces coincide con un punto crítico.
Solución:
La derivada de una función permite conocer la pendiente de la recta tangente a la curva en todos los puntos de su dominio. Las funciones que se muestran en los incisos tienen 2 números críticos: un mínimo y un máximo, por lo tanto, la derivada de la función cambia de signo 2 veces en todas.
En la primera y la tercera el cambio es: negativo, positivo, negativo; mientras que en la segunda el cambio es positivo, negativo, positivo. Debido a que todas cumplen con la cantidad de cambios de signo, decidimos la respuesta correcta por el número crítico.
Las raíces de un polinomio son los cruces con el eje x de la función. Por lo tanto, hay que identificar cuál de las gráficas tiene un máximo o mínimo sobre el eje x . Esto corresponde con la gráfica del inciso a).
El resto de incisos no pueden ser la respuesta correcta, porque sus números críticos no coinciden con alguna de las raíces del polinomio.
Reactivo 17
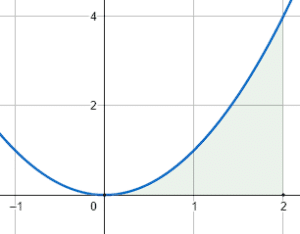
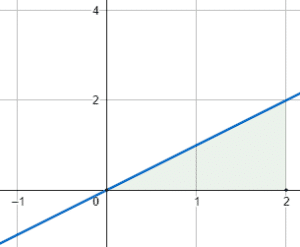
Seleccione la gráfica que refleja la resolución de la integral.
{\int }_{0}^{2}2xdx
Solución:
A partir de la integral definida se identifican 2 elementos importantes: los límites de integración \left[\mathrm{0,2}\right] y la función f\left(x\right)=2x . Todas las imágenes muestran integrales definidas entre 0 y 2, pero solo la del inciso b) muestra la integral sobre una línea recta.
Por lo tanto, la respuesta correcta es el inciso b). Las otras dos gráficas corresponden a integrar una parábola, no una recta. Probablemente hayas confundido la primitiva (resultado de la integral) con la función a integrar.
Reactivo 18
Relacione cada propiedad de los límites con la solución correspondiente para dos funciones f(x) y g(x) cuyos límites existen.

- 1a, 2c, 3b
- 1b, 2c, 3a
- 1c, 2b, 3a
Solución:
Vamos a examinar cada una de las propiedades en la columna izquierda, para relacionarla con la solución correspondiente en la columna derecha.
El límite del producto de dos funciones, es igual al producto de los límites de cada función.
\underset{x\to c}{\mathrm{lim}}\left[f\left(x\right)g\left(x\right)\right]=\underset{x\to c}{\mathrm{lim}}f\left(x\right)\cdot \underset{x\to c}{\mathrm{lim}}g\left(x\right)
Por lo tanto: 1b). Solo el inciso b) inicia con 1b… concluimos entonces que la respuesta correcta es el inciso b). En la opción a) se relaciona de manera incorrecta la propiedad del producto con la de multiplicación por un escalar.
El error en el inciso c) ocurre al confundir la propiedad del cociente con la propiedad del límite del producto de dos funciones.
Reactivo 19
La relación entre la distancia recorrida en metros por un móvil y el tiempo en segundos es s\left(t\right)=t\left(1.5t-2\right) . ¿Cuál es la velocidad instantánea que lleva el móvil a los 4 segundos?
- 10 m/s
- 12 m/s
- 16 m/s
Solución:
Primero hay que derivar la función de la distancia en función del tiempo para obtener la de velocidad instantánea.
v\left(t\right)=\frac{ds\left(t\right)}{dt}=\frac{d\left(1.5{t}^{2}-2t\right)}{dt}=3t-2
v\left(t\right)=3t-2
Ahora, sustituimos t=4 \mathrm{s} .
v\left(t=4\right)=3\left(4\right)-2=12-2=10 \mathrm{m}/\mathrm{s}
La velocidad instantánea del móvil es de 10 metros por segundo.
La respuesta correcta es el inciso a). El error en el inciso b) ocurre al derivar el término 2t , has considerado la derivada de la constante y por ello, el término se anula y la derivada queda: v\left(t\right)=3t . Por otro lado, en el inciso c) no se ha derivado la función, se aplica sustitución directa.
Reactivo 20
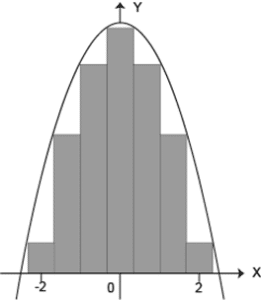
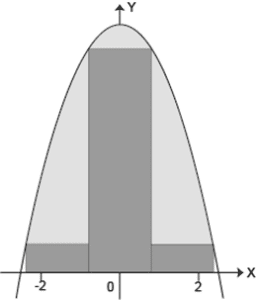
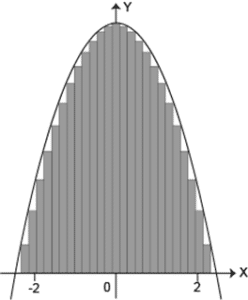
Identifique la partición que más se aproxima al área bajo la curva.
Solución:
Antes de llegar a la integración definida, se estudian varios métodos para calcular el área debajo de una curva, entre los que se encuentra el método de aproximación mediante rectángulos.
En dicho método existen dos variantes: aproximación por exceso, donde una parte de los rectángulos supera a la curva y aproximación por déficit, donde los rectángulos no rellenan una pequeña parte del área de la curva.
El punto de estos métodos es que, mientras mayor sea el número de rectángulos, menor será el error y más cercana será la aproximación. Esto se logra disminuyendo la anchura o partición de los rectángulos.
Teniendo esto en cuenta y examinando los incisos, aquel con mayor cantidad de rectángulos es el c). Con este planteamiento como base, se construyen las sumas de Riemann y con ellas se llega a la definición de integrales definidas.
El error en los otros dos incisos, consta en no considerar la cantidad de rectángulos dentro de la curva. Si has seleccionado alguna de ellas, es necesario que tengas en cuenta la explicación anterior.
Reactivo 21
Identifique la función que se resuelve como integral inmediata mediante manipulación algebraica.
- \int {x}^{5}+2 dx
- \int {\left(x+2\right)}^{5}dx
- \int x{\left(x+2\right)}^{5}dx
Solución:
En el caso de la primera integral, habría que aplicar la propiedad de la integral de una suma, pero el integrando no se encuentra correctamente delimitado por paréntesis. Esta no es la respuesta correcta.
Por otro lado, la integral del inciso b) se puede resolver de forma inmediata con la fórmula para una potencia, porque el diferencial de x+2 es el mismo que para x . Por esta razón, se puede aplicar la fórmula sin mayor modificación.
La respuesta correcta es la opción b). Finalmente, la integral del inciso c) se resuelve por el método de integración por partes.
Reactivo 22
Seleccione el límite de la función f\left(x\right)=9{x}^{2}+12x+3 , por medio del cual se obtiene la derivada por definición.
- \underset{x\to {x}_{0}}{\mathrm{lim}}\frac{\left(9{x}^{2}+12x+3\right)-9{x}_{0}^{2}+12{x}_{0}+3}{x-{x}_{0}}
- \underset{x\to {x}_{0}}{\mathrm{lim}}\frac{\left(9{x}^{2}+12x+3\right)-\left(9{x}_{0}^{2}+12{x}_{0}+3\right)}{x-{x}_{0}}
- \underset{x\to {x}_{0}}{\mathrm{lim}}\frac{\left(9{x}_{0}^{2}+12{x}_{0}+3\right)-\left(9{x}^{2}+12x+3\right)}{x-{x}_{0}}
Solución:
Recordemos la definición de la derivada.
{f}^{\text{'}}\left(x\right)=\underset{x\to {x}_{o}}{\mathrm{lim}}\frac{f\left(x\right)-f\left({x}_{o}\right)}{x-{x}_{o}}
Esta es una de las formas en que se puede escribir la definición, empleamos esta porque los incisos muestran las opciones en base a ella. Examinando el límite, solo nos queda encontrar a f\left({x}_{o}\right) para sustituir todos los elementos.
f\left({x}_{o}\right)=9{x}_{o}^{2}+12{x}_{o}+3
Sustituimos todo en el límite.
{f}^{\text{'}}\left(x\right)=\underset{x\to {x}_{o}}{\mathrm{lim}}\frac{\left(9{x}^{2}+12x+3\right)-\left(9{x}_{o}^{2}+12{x}_{o}+3\right)}{x-{x}_{o}}
La respuesta correcta es el inciso b). El error en el inciso a) es que no se colocaron los paréntesis y el signo menos solo afectó a 9{x}_{o}^{2} . Por otra parte, en la opción c) se escriben al revés los valores de f\left(x\right) y f\left({x}_{o}\right) , esto nos daría el negativo de la derivada.
Reactivo 23
Determine el área encerrada por la función f\left(x\right) = 4 - {x}^{2} y el eje x.
- \frac{16}{3}{u}^{2}
- \frac{32}{3}{u}^{2}
- \frac{48}{3}{u}^{2}
Solución:
Para calcular el área entre la función y el eje x , debemos calcular las raíces del polinomio, estos serán nuestros límites de integración.
4-{x}^{2}=0\to \left(2-x\right)\left(2+x\right)=0
x=2, x=-2
Los límites de integración son: \left[-2, 2\right] . La integral definida quedaría como:
{\int }_{-2}^{2}\left(4-{x}^{2}\right)dx
Separamos la integral con la propiedad correspondiente y resolvemos.
{\int }_{-2}^{2}\left(4-{x}^{2}\right)dx=4{\int }_{-2}^{2}dx-{\int }_{-2}^{2}{x}^{2}dx=\left.4x-\frac{{x}^{3}}{3}\right]\begin{array}{c}2\\ \\ -2\end{array}
Evaluando nos queda:
\left.4x-\frac{{x}^{3}}{3}\right]\begin{array}{c}2\\ \\ -2\end{array}=4\left(2\right)-\frac{{2}^{3}}{3}-\left[4\left(-2\right)-\frac{{\left(-2\right)}^{3}}{3}\right]=8-\frac{8}{3}+8-\frac{8}{3}
8-\frac{8}{3}+8-\frac{8}{3}=\frac{32}{3} {u}^{2}\approx 10.66 {u}^{2}
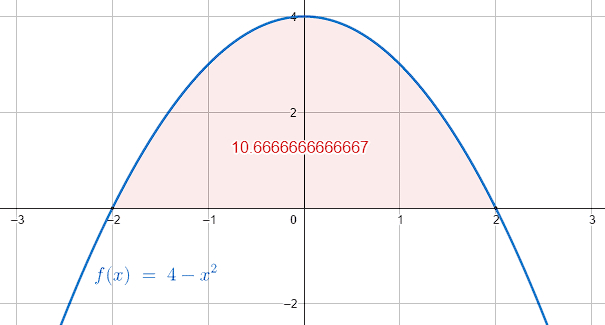
La respuesta correcta es el inciso b). El resultado del inciso a) se debe a un error con los límites de integración. En lugar de seleccionar \left[-\mathrm{2,2}\right] has utilizado \left[\mathrm{0,2}\right] obteniendo como resultado \frac{16}{3} . Incluso, como la función es simétrica respecto al eje y , el valor es la mitad de \frac{32}{3} .
Por otra parte, en el inciso c) el error ocurre al evaluar el límite inferior en la primitiva. El cubo de -2 debería ser negativo, pero se consideró positivo.
Reactivo 24
Calcule el valor de la integral definida de la función.
{\int }_{1}^{4}\left({x}^{2}+x\right)dx
- -\frac{171}{6}
- \frac{171}{6}
- \frac{181}{6}
Solución:
Iniciamos separando la integral en dos con la propiedad correspondiente.
{\int }_{1}^{4}\left({x}^{2}+x\right)dx={\int }_{1}^{4}{x}^{2}dx+{\int }_{1}^{4}xdx=\left.\frac{{x}^{3}}{3}+\frac{{x}^{2}}{2}\right]\begin{array}{c}4\\ \\ 1\end{array}
Evaluamos los límites en la primitiva empleando el teorema fundamental del cálculo.
\left.\frac{{x}^{3}}{3}+\frac{{x}^{2}}{2}\right]\begin{array}{c}4\\ \\ 1\end{array}=\frac{{4}^{3}}{3}+\frac{{4}^{2}}{2}-\left(\frac{{1}^{3}}{3}+\frac{{1}^{2}}{2}\right)=\frac{64}{3}+8-\frac{1}{3}-\frac{1}{2}
\frac{64}{3}+8-\frac{1}{3}-\frac{1}{2}=\frac{171}{6} {u}^{2}
Finalmente:
{\int }_{1}^{4}\left({x}^{2}+x\right)dx=\frac{171}{6} {u}^{2}
La respuesta correcta es la opción b). El error en el inciso a) consta en invertir los términos al evaluar los extremos de integración F\left(a\right)-F\left(b\right) en lugar de F\left(b\right)-F\left(a\right) . Por otro lado, en la opción c) se calcula una suma F\left(b\right)+F\left(a\right) en lugar de una resta F\left(b\right)-F\left(a\right) .