Iniciamos la solución de la Guía Interactiva de EXANI II, en el módulo de Cálculo Diferencial e Integral. En este tutorial resolveremos desde el reactivo 1 hasta el 12.

En una materia como cálculo, es importante que tengas buenas bases de álgebra e identidades trigonométricas. Esto te permitirá resolver los ejercicios con mayor rapidez.
Estructura del EXANI II
La prueba de ingreso EXANI II se divide en dos áreas:
- Habilidades y conocimientos
- Los módulos específicos
Algunas universidades aplican una prueba diagnóstico de inglés extra, la cual no cuenta para aprobar el examen.
Examen de habilidades y conocimientos
La primera parte del EXANI II 2024 se aplica para todas las carreras y se compone de 90 reactivos: 60 de Español y 30 de Matemáticas. La siguiente tabla resume la distribución de los reactivos en la prueba de ingreso EXANI II:
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Conocimientos específicos
Conocimientos específicos del EXANI II posee un total de 15 módulos en los que se encuentra Cálculo Diferencial e Integral.
Todos los estudiantes deben responder 2 módulos en esta segunda parte, los cuales varían de acuerdo con la carrera. Es necesario que revises la convocatoria de tu universidad para conocer qué módulos van para tu examen.
| 1. Administración | 9. Física |
| 2. Aritmética | 10. Historia |
| 3. Biología | 11. Literatura |
| 4. Cálculo diferencial e integral | 12. Matemáticas financieras |
| 5. Ciencias de la Salud | 13. Premedicina |
| 6. Derecho | 14. Probabilidad y estadística |
| 7. Economía | 15. Química |
| 8. Filosofía | 16. Psicología |
Temario Cálculo diferencial e integral EXANI II
En la siguiente tabla te mostramos la distribución de los 24 reactivos de cálculo diferencial e integral, con el temario desglosado que va para el examen.
| Subárea | Reactivos |
|---|---|
| Cálculo diferencial | 12 |
| Cálculo Integral | 12 |
| Total | 24 |
Subárea: Cálculo diferencial
- Propiedades de los límites
- Límites de funciones polinomiales y con variables independientes
- Derivadas por definición, de funciones trigonométricas, de funciones exponenciales y logarítmicas y de funciones polinomiales
- Recta tangente de funciones algebraicas
- Aplicaciones físicas de la derivada (velocidad instantánea, distancia, rapidez de cambio y de optimización)
Subárea: Cálculo integral
- Partición de funciones
- Manipulación algebraica y aritmética
- Propiedades de la integral
- Métodos de integración
- Problemas de área, volumen y movimiento con integrales definidas
Recomendaciones para resolver la guía interactiva
Te dejo algunos trucos para sacarle el máximo provecho a la guía EXANI II 2024 que puedes tener en cuenta a la hora de estudiar:
- Elimina las distracciones. Ve a un sitio en el que te sientas cómodo o cómoda, coloca tu teléfono en modo avión y mantén cerca de ti lapiceros, borrador y libretas.
- No te enfoques en el resultado, sino en el procedimiento. Coloca toda tu atención en analizar y desglosar los problemas para identificar las herramientas que debes usar. Una buena estrategia conlleva a buenos resultados.
- Lleva el tiempo mientras resuelves la guía. Mide el tiempo durante cada sesión de estudios, buscando acortar el tiempo lo más que puedas antes del examen.
- Si un reactivo parece demasiado difícil, ve al siguiente. Evita caer en frustración mientras estudias, mantener el foco y meditar esos ejercicios difíciles, te permitirán desarrollar capacidades analíticas sólidas.
Reactivo 1
Seleccione el valor del límite en la siguiente función.
\underset{x\to -2}{\mathrm{lim}}2{x}^{3}+2{x}^{2}+2
- -22
- -6
- 26
Solución:
Este límite se resuelve mediante sustitución directa, ya que las funciones polinómicas no presentan indeterminaciones en ningún punto de su dominio.
Evaluamos el límite:
\underset{x\to -2}{\mathrm{lim}}2{x}^{3}+2{x}^{2}+2=2{\left(-2\right)}^{3}+2{\left(-2\right)}^{2}+2=-2\cdot 8+2\cdot 4+2
\underset{x\to -2}{\mathrm{lim}}2{x}^{3}+2{x}^{2}+2=-6
El límite cuando x tiende a -2 de 2{x}^{3}+2{x}^{2}+2 , es igual a 26.
La respuesta correcta es el inciso b). Tanto en el inciso a) como en el c) se realiza una mala sustitución del valor de x en la función.
En el primer caso, se eleva al cuadrado -2 pero se conserva el signo negativo, mientras que en el tercero se eleva al cubo -2 pero el resultado se toma positivo.
Reactivo 2
Identifique la derivada de la función.
f\left(x\right)={e}^{{x}^{6}}
- {e}^{{x}^{6}}
- 6{x}^{5}{e}^{{x}^{6}}
- 6{x}^{6}{e}^{{x}^{6}}
Solución:
Aplicando la regla de la cadena, se inicia derivando con la fórmula de la exponencial.
{f}^{\text{'}}\left(x\right)={\left[{e}^{{x}^{6}}\right]}^{\text{'}}={\left({x}^{6}\right)}^{\text{'}}\cdot {e}^{{x}^{6}}
Ahora, se resuelve la derivada indicada con la fórmula para una potencia.
{f}^{\text{'}}\left(x\right)=6{x}^{5}{e}^{{x}^{6}}
La respuesta correcta es el inciso b). El error en el inciso a), radica en ignorar la derivada del exponente. Por otra parte, en el inciso c) se aplica correctamente la fórmula de la exponencial pero no la de una potencia.
Reactivo 3
Calcule la integral de la función trigonométrica.
\int {\mathrm{sin}}^{3}2xdx
- -\frac{\mathrm{cos}2x}{2}-\frac{{\mathrm{cos}}^{3}2x}{6}+C
- -\frac{\mathrm{cos}2x}{2}+\frac{{\mathrm{cos}}^{3}2x}{6}+C
- \frac{\mathrm{cos}2x}{2}+\frac{{\mathrm{cos}}^{3}2x}{6}+C
Solución:
Primero, se separa en factores el integrando de la siguiente forma:
\int {\mathrm{sin}}^{3}2xdx=\int {\mathrm{sin}}^{2}\left(2x\right)\mathrm{sin}\left(2x\right)dx
Ahora, se aplica la identidad pitagórica.
{\mathrm{sin}}^{2}\left(2x\right)+{\mathrm{cos}}^{2}\left(2x\right)=1\to {\mathrm{sin}}^{2}\left(2x\right)=1-{\mathrm{cos}}^{2}\left(2x\right)
Sustituyendo:
\int {\mathrm{sin}}^{2}\left(2x\right)\mathrm{sin}\left(2x\right)dx=\int \left(1-{\mathrm{cos}}^{2}\left(2x\right)\right)\mathrm{sin}\left(2x\right)dx
Se separa en dos la integral con la propiedad de la integral de una suma.
\int \left(1-{\mathrm{cos}}^{2}\left(2x\right)\right)\mathrm{sin}\left(2x\right)dx=\int \mathrm{sin}2xdx-\int {\mathrm{cos}}^{2}\left(2x\right)\mathrm{sin}\left(2x\right)dx
La primera integral se resuelve multiplicando y dividiendo por 2.
{I}_{1}=\frac{1}{2}\int \mathrm{sin}2x2dx=-\frac{1}{2}\mathrm{cos}\left(2x\right)+{C}_{1}
Por otra parte, en la segunda integral es necesario aplicar cambio de variable.
{I}_{2}=\int {\mathrm{cos}}^{2}\left(2x\right)\mathrm{sin}\left(2x\right)dx
u=\mathrm{cos}2x\to du=-2\mathrm{sin}2xdx
2\mathrm{sin}2xdx=-\frac{1}{2}du
Aplicando el cambio de variables se obtiene:
\int {\mathrm{cos}}^{2}\left(2x\right)\mathrm{sin}\left(2x\right)dx\to -\frac{1}{2}\int {u}^{2}du
Esta integral se resuelve de forma inmediata con la fórmula para una potencia.
-\frac{1}{2}\int {u}^{2}du=-\frac{{u}^{3}}{6}+{C}_{2}
Devolviendo el cambio de variable:
-\frac{{u}^{3}}{6}+{C}_{2}\to -\frac{{\mathrm{cos}}^{3}2x}{6}+{C}_{2}
Sustituyendo ambas soluciones parciales en la integral original:
I=-\frac{\mathrm{cos}\left(2x\right)}{2}+\frac{{\mathrm{cos}}^{3}2x}{6}+C
Finalmente:
\int {\mathrm{sin}}^{3}2xdx=-\frac{\mathrm{cos}2x}{2}+\frac{{\mathrm{cos}}^{3}2x}{6}+C
Comparando con los incisos, la respuesta correcta es el b). En el inciso a) se comete un error con el signo negativo al sustituir la solución de la segunda integral. Por otro lado, en el inciso c) no se considera el signo negativo en la integral de seno.
Reactivo 4
¿Qué propiedad se utiliza para resolver la siguiente integral?
{\int }_{1}^{-2} \left(x+1\right)dx
- {\int }_{b}^{a} f\left(x\right)dx=-{\int }_{a}^{b} f\left(x\right)dx
- {\int }_{b}^{a} f\left(x\right)dx={\int }_{a}^{b} f\left(x\right)dx
- {\int }_{b}^{a} kf\left(x\right)dx=k{\int }_{b}^{a} f\left(x\right)dx
Solución:
Para aplicar el teorema fundamental del cálculo al resolver integrales definidas, los extremos de integración deben ir de menor (abajo) a mayor (arriba). Debido a que los límites están invertidos, se pueden acomodar aplicando la siguiente propiedad.
{\int }_{b}^{a} f\left(x\right)dx=-{\int }_{a}^{b} f\left(x\right)dx
Concluimos indicando como respuesta correcta al inciso a). La opción b) intercambia de lugar a los extremos de integración pero no coloca el signo negativo, mientras que en la c) se utiliza la propiedad de la integral de una constante por una función.
Reactivo 5
Identifique la sustitución que ayuda a resolver la integral de la función.
\int \frac{2}{\sqrt{6-6{x}^{2}}}dx
- x=\mathrm{sec}\alpha
- x=\mathrm{tan}\alpha
- x=\mathrm{cos}\alpha
Solución:
Iniciamos extrayendo factor común el 6 del denominador.
\int \frac{2}{\sqrt{6-6{x}^{2}}}dx=\frac{2}{\sqrt{6}}\int \frac{1}{\sqrt{1-{x}^{2}}}dx
A partir del radicando, sabemos que el 1 debe ser la hipotenusa del triángulo rectángulo y que x uno de los catetos. Debido a que en los incisos se encuentra la identidad coseno, relacionamos a x con el cateto adyacente a \theta .
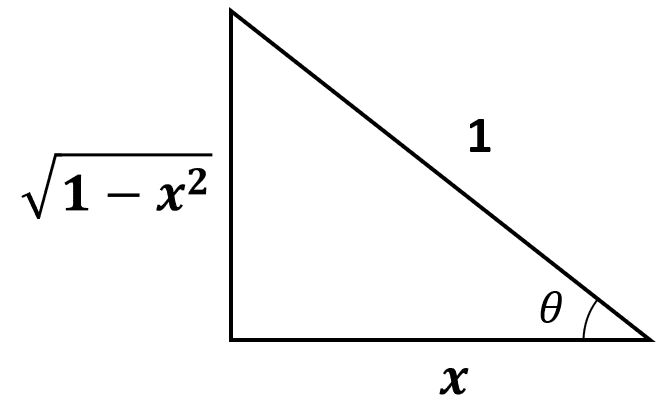
Por lo tanto: x=\mathrm{cos}\theta .
La respuesta correcta es el inciso c). La opción a) no puede ser la respuesta correcta ya que la identidad trigonométrica es {\mathrm{tan}}^{2}\alpha ={\mathrm{sec}}^{2}\alpha -1 . Este cambio de variable no simplifica la integral.
Por otro lado, el cambio del inciso b) x=\mathrm{tan}\alpha tampoco simplifica la integral ya que la identidad trigonométrica es {\mathrm{tan}}^{2}\alpha +1={\mathrm{sec}}^{2}\alpha , resultando en una integral trigonométrica muy compleja.
Reactivo 6
Seleccione la ecuación de la recta tangente a la gráfica de la función f\left(x\right)=3{x}^{2}+4 en el punto P\left(\mathrm{1,7}\right) .
- y=6x+1
- y=6x-41
- y=7x+0
Solución:
Para obtener la ecuación solicitada, empleamos la forma punto pendiente de la recta.
y-{y}_{o}=m\left(x-{x}_{o}\right)
El punto viene indicado por el enunciado y la pendiente se obtiene al evaluar la derivada de f en x=1 . Recordemos que:
m={f}^{\text{'}}\left({x}_{o}\right)
Calculamos la derivada de la función.
{f}^{\text{'}}\left(x\right)={\left(3{x}^{2}+4\right)}^{\text{'}}=6x
Evaluamos x=1 .
m={f}^{\text{'}}\left(1\right)=6\left(1\right)=6
Finalmente, sustituimos las coordenadas del punto y la pendiente.
y-7=6\left(x-1\right)\to y=6x-6+7
\therefore y=6x+1
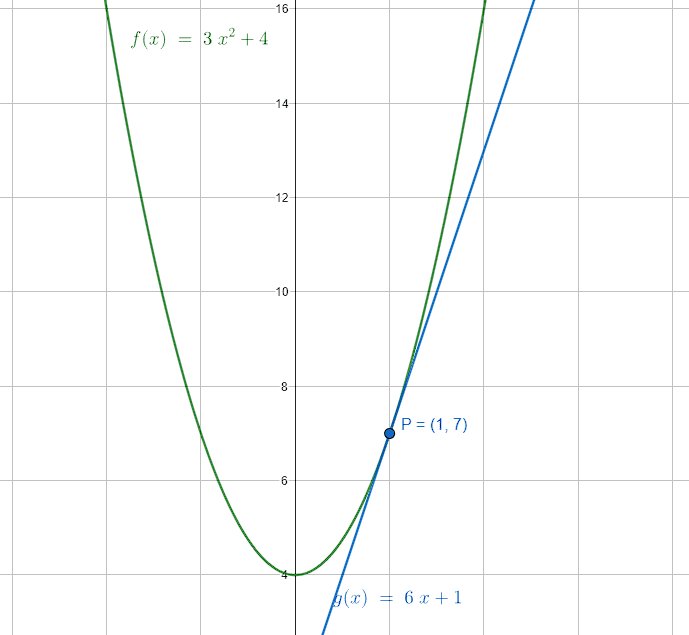
La respuesta correcta es el inciso a). El error en el inciso b) ocurre al sustituir las coordenadas x y y del punto, mientras que en el inciso c) calcula la pendiente sustituyendo x=1 en función y no en la derivada.
Reactivo 7
Calcule el valor del límite en la función.
\underset{x\to \mathrm{\infty }}{lim} \frac{3-6{x}^{2}}{5x+9{x}^{2}}
- -\frac{3}{9}
- -\frac{2}{3}
- -\frac{3}{2}
Solución:
Aunque siempre se deben evaluar los límites para identificar el tipo de indeterminación que presentan, en los casos donde tenemos límites al infinito de fracciones con polinomios, la indeterminación siempre es \infty /\infty .
Se divide toda la expresión entre la máxima potencia de x , es decir: {x}^{2} .
\underset{x\to \mathrm{\infty }}{lim} \frac{\frac{3}{{x}^{2}}-\frac{6{x}^{2}}{{x}^{2}}}{\frac{5x}{{x}^{2}}+\frac{9{x}^{2}}{{x}^{2}}}=\underset{x\to \mathrm{\infty }}{lim} \frac{\frac{3}{{x}^{2}}-6}{\frac{5}{x}+9}
Evaluamos para comprobar la ruptura de la indeterminación. Recordemos que un número dividido por infinito es cero.
\underset{x\to \mathrm{\infty }}{lim} \frac{\frac{3}{{x}^{2}}-6}{\frac{5}{x}+9}=\frac{\frac{3}{\infty }-6}{\frac{5}{\infty }+9}=-\frac{6}{9}=-\frac{2}{3}
El límite cuando x tiende a infinito de \frac{3-6{x}^{2}}{5x+9{x}^{2}} es -\frac{2}{3} .
La respuesta correcta es el inciso b). El error en el inciso a) ocurre al simplificar de manera incorrecta la fracción.
Por otra parte, en el inciso c) el error ocurre al aplicar una propiedad de los límites al infinito de funciones racionales. Si el grado de los polinomios es igual, el resultado del límite tiende al cociente del coeficiente de mayor grado del numerador sobre el del denominador.
Empleando esta propiedad, has invertido la posición del numerador y denominador en la respuesta.
Reactivo 8
¿Cuál es la derivada del cociente \frac{2x+5}{{x}^{2}} ?
- \frac{-2{x}^{2}-10x}{{x}^{4}}
- \frac{-2{x}^{2}+10x}{{x}^{4}}
- \frac{2{x}^{2}-10x}{{x}^{4}}
Solución:
La expresión se deriva aplicando la fórmula para un cociente de funciones.
{\left(\frac{u}{v}\right)}^{\text{'}}=\frac{{u}^{\text{'}}v-v\text{'}u}{{v}^{2}}
En nuestro caso: u=2x+5 y v={x}^{2} . Aplicando la fórmula de derivación se obtiene:
{\left(\frac{2x+5}{{x}^{2}}\right)}^{\text{'}}=\frac{\left(2x+5\right)\text{'}\left({x}^{2}\right)-\left({x}^{2}\right)\text{'}\left(2x+5\right)}{{\left({x}^{2}\right)}^{2}}
Las derivadas indicadas se resuelven con la fórmula para derivar una suma y para derivar una potencia.
\frac{\left(2x+5\right)\text{'}\left({x}^{2}\right)-\left({x}^{2}\right)\text{'}\left(2x+5\right)}{{\left({x}^{2}\right)}^{2}}=\frac{2\left({x}^{2}\right)-2x\left(2x+5\right)}{{x}^{4}}
\frac{2\left({x}^{2}\right)-2x\left(2x+5\right)}{{x}^{4}}=\frac{2{x}^{2}-4{x}^{2}-10x}{{x}^{4}}=\frac{-2{x}^{2}-10x}{{x}^{4}}
Finalmente:
{\left(\frac{2x+5}{{x}^{2}}\right)}^{\text{'}}=\frac{-2{x}^{2}-10x}{{x}^{4}}
La respuesta correcta es el inciso a). En el inciso b) el error ocurre al momento de resolver la propiedad distributiva -2x\left(2x+5\right) , no se aplica correctamente la ley de los signos para la multiplicación.
En el inciso c) ocurre algo similar, pero en la suma de 2{x}^{2}-4{x}^{2} , se aplica de manera incorrecta la propiedad de los signos de la suma.
Reactivo 9
Calcule la derivada de la función polinomial.
f\left(x\right)={x}^{3}+4{x}^{2}+2x-7
- 3{x}^{2}+8x
- 3{x}^{2}+8x+2
- 3{x}^{2}+8x+2-7
Solución:
Para derivar al polinomio, se aplica la propiedad de la derivada de una suma y las fórmulas de la derivada de una potencia y de una constante.
{f}^{\text{'}}\left(x\right)={\left({x}^{3}+4{x}^{2}+2x-7\right)}^{\text{'}}
{f}^{\text{'}}\left(x\right)={\left({x}^{3}\right)}^{\text{'}}+{\left(4{x}^{2}\right)}^{\text{'}}+{\left(2x\right)}^{\text{'}}-\left(7\right)\text{'}
Resolviendo las derivadas indicadas se obtiene:
{f}^{\text{'}}\left(x\right)=3{x}^{2}+8x+2
La respuesta correcta es el inciso b). El error en el inciso a) radica en considerar que la derivada de una constante por x es igual a cero, mientras que en el inciso c) considera que la derivada de una constante permanece igual o, que no se deriva.
Reactivo 10
Identifique la derivada de la composición f(g(x)) considerando las siguientes funciones.
f\left(x\right)=\sqrt{x}
g\left(x\right)={x}^{3}+3{x}^{2}+1
- \frac{3{x}^{2}+6x}{2\sqrt{{x}^{3}+3{x}^{2}+1}}
- \sqrt{3{x}^{2}+6x}
- \sqrt{{x}^{3}+3{x}^{2}+1}
Solución:
Esta derivada se puede resolver mediante dos enfoques: aplicando la definición de regla de la cadena \frac{df\left(g\right)}{dx}=\frac{df\left(g\right)}{dg}\cdot \frac{dg}{dx} o, calculando la composición de f con g y luego derivando respecto de x .
Vamos a aplicar el primer método, porque es la intención del ejercicio. Al final mostraremos cómo se hace de la segunda forma.
Composición de las funciones.
f\left[g\left(x\right)\right]=\sqrt{{x}^{3}+3{x}^{2}+1}
Calculando la derivada \frac{df\left(g\right)}{dg} .
\frac{df\left(g\right)}{dg}=\frac{d\left(\sqrt{{x}^{3}+3{x}^{2}+1}\right)}{d\left({x}^{3}+3{x}^{2}+1\right)}=\frac{d\left[{\left({x}^{3}+3{x}^{2}+1\right)}^{1/2}\right]}{d\left({x}^{3}+3{x}^{2}+1\right)}
Empleamos la fórmula para la derivada de una potencia. Hay que tener en cuenta que {x}^{3}+3{x}^{2}+1 es nuestra variable a derivar. Podemos aplicar un sencillo cambio de variable para facilitar la notación.
u={x}^{3}+3{x}^{2}+1
\frac{d\left[{\left({x}^{3}+3{x}^{2}+1\right)}^{1/2}\right]}{d\left({x}^{3}+3{x}^{2}+1\right)}=\frac{d\left({u}^{1/2}\right)}{du}=\frac{1}{2}{u}^{-1/2}=\frac{1}{2\sqrt{u}}
Sustituyendo.
\frac{df\left(g\right)}{dg}=\frac{1}{2\sqrt{{x}^{3}+3{x}^{2}+1}}
Ahora, se calcula la derivada \frac{dg}{dx} .
\frac{dg}{dx}=\frac{d\left({x}^{3}+3{x}^{2}+1\right)}{dx}=3{x}^{2}+6x
Finalmente:
\frac{df\left(g\right)}{dx}=\frac{df\left(g\right)}{dg}\cdot \frac{dg}{dx}=\frac{3{x}^{2}+6x}{2\sqrt{{x}^{3}+3{x}^{2}+1}}
La solución parece extensa porque hemos explicado cada paso a detalle, pero con práctica, suele quedar en un par de pasos. La respuesta correcta es el inciso a).
En la opción b) se plantea la composición, pero únicamente deriva g y sustituye en f, aplica mal la regla de la cadena. Por otra parte, en el inciso c) sólo se plantea la composición, pero no se deriva.
Reactivo 11
Calcule la siguiente integral.
\int \mathrm{cos}2xdx
- 2\mathrm{sin}2x+C
- \mathrm{sin}\frac{x}{2}+C
- \frac{\mathrm{sin}2x}{2}+C
Solución:
La integral puede resolverse aplicando sustitución al argumento del coseno.
u=2x\to du=2dx
dx=\frac{1}{2}du
Aplicando el cambio.
\int \mathrm{cos}2xdx\to \frac{1}{2}\int \mathrm{cos}udu
Esta integral es inmediata.
\frac{1}{2}\int \mathrm{cos}udu=\frac{1}{2}\mathrm{sin}u+C
Devolvemos el cambio de variable.
\frac{1}{2}\mathrm{sin}u+C\to \frac{1}{2}\mathrm{sin}2x+C
Finalmente:
\int \mathrm{cos}2xdx=\frac{1}{2}\mathrm{sin}2x+C
La respuesta correcta es el inciso c). El error en el inciso a) es que se obtiene la derivada en lugar de la integral, mientras que en el inciso b) se divide al argumento del seno por 2 en lugar de dividir a la función.
Reactivo 12
Calcule la distancia en metros que recorre en los primeros 4 segundos una piedra que se arroja desde un edificio si ésta tiene en el instante t = 0 una velocidad de v = 9.8 t + 8.
- 9.8
- 51.6
- 110.4
Solución:
A partir de las relaciones de la cinemática clásica, sabemos que podemos encontrar la distancia recorrida por un cuerpo, integrando de forma definida su velocidad.
d=\underset{{t}_{1}}{\overset{{t}_{2}}{\int }}v\left(t\right)dt
En este caso: {t}_{1}=0 , {t}_{2}=4 y v\left(t\right)=9.8t+8 . Sustituimos e integramos aplicando el teorema fundamental del cálculo para integrales definidas.
d=\underset{0}{\overset{4}{\int }}\left(9.8t+8\right)dt=9.8\underset{0}{\overset{4}{\int }}tdt+8\underset{0}{\overset{4}{\int }}dt
9.8\underset{0}{\overset{4}{\int }}tdt+8\underset{0}{\overset{4}{\int }}dt=\left.\frac{9.8{t}^{2}}{2}+8t\right]\begin{array}{c}4\\ \\ 0\end{array}
Evaluando la primitiva nos queda:
d=\left[\frac{9.8}{2}{\left(4\right)}^{2}+8\left(4\right)\right]-\left[\frac{9.8}{2}{\left(0\right)}^{2}+8\left(0\right)\right]
d=110.4 \mathrm{m}
El cuerpo que se desplaza con una velocidad v\left(t\right)=9.8t+8 , recorre 110.4 metros desde el segundo 0 hasta el segundo 4. La respuesta correcta es el inciso c).
El error de la opción a) es que se deriva la velocidad, mientras que en el b) se integra correctamente, pero al sustituir el límite superior, este no se elevó al cuadrado obteniendo 51.6 \mathrm{m} .

