¡Hola aspirante! En este post vamos a resolver la primera parte de la guía interactiva Exani II en el área de pensamiento matemático. Recuerda que la nueva versión del Exani II de Ceneval sigue tomando en cuenta las matemáticas entre las áreas fundamentales para determinar el resultado final de tu examen de admisión.

Este es un breve resumen del Exani II:
- Desarrollo: Ceneval
- Examen de admisión: Exani II
- Reactivos: 168
- Tipo: Opción multiple
- Duración: 4 horas y media
- Modalidades: Presencial, en línea y desde casa.
A partir del verano de 2021 el Exani II tiene una nueva estructura del examen, esto quiere decir nuevos temas, nuevos reactivos y un nuevo tipo de formato en las preguntas. Por lo que te recomiendo revisar toda la información disponible sobre los otros módulos de estudio.
Recuerda que este examen es desarrollado por el Ceneval un organismo independiente a tu universidad.
Estructura del Exani II
Antes de comenzar con la solución de la guía en la parte de pensamiento matemático es muy importante que te quede claro la estructura del Exani II.
A grandes rasgos el nuevo examen incluye las siguientes áreas:
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Tabla Estructura Exani II
Te repito que este año cambiaron el examen, si bien no es un cambio radical, algunas áreas de la versión anterior desaparecieron y agregaron nuevos módulos a las especialidades y áreas de estudio.
Si quieres conocer en detalle todos los cambios del nuevo Exani II ingresa al siguiente post en donde te explicamos todos los cambios y los temas que tienes que estudiar.
Temario pensamiento matemático
La parte de pensamiento matemático es considerada por muchos como más complicada de la guía de estudios del Exani II.
Es muy importante que domines la parte de matemáticas, ya que representa gran parte de tu puntaje final en el examen de ingreso a la Universidad.
A continuación te muestro los temas que abarcan el área de pensamiento matemático de la guía Exani II de ceneval.
En la siguiente tabla te mostramos la distribución de los 30 reactivos de pensamiento matemático y los temas que van para el examen.
| Subárea | Tema | Num. de reactivos |
|---|---|---|
| Comprensión de lo matemático | Conexiones | 18 |
| Estimación | ||
| Sentido matemático | ||
| Matematización | Desarrollo de usos | 12 |
| Lenguaje matemático | ||
| Resignificaciones | ||
| Total | 30 |
Algunos temas específicos son:
- Inecuaciones lineales
- Simplificación de expresiones algebraicas
- Razones trigonométricas
- Área
- Desviación estándar
- Media aritmética
- Razones y proporciones
- Interpretación gráfica de ecuaciones lineales
- Ejes de simetría
- Estimación de trayectorias
- Frecuencias
- Probabilidad clásica de eventos simples
- Leyes de los exponentes
- Porcentaje
- Unidades de medida como patrón de comparación
- Espacio muestral
- Representación gráfica de ecuaciones de segundo grado
- Comportamiento gráfico de funciones cuadráticas
- Relaciones trigonométricas
- Representación gráfica de información
- Medidas de tendencia central y de dispersión
- Polinomios
- Sistemas de ecuaciones lineales con dos y tres incógnitas
- Variación lineal tabular
- Medidas de posición (deciles, cuartiles y percentiles)
¿Qué tan difícil es el módulo de matemáticas del Exani II?
Esta es la típica pregunta que hacemos, o nos hacen cuando salimos del salón después de terminar un examen (el que sea, no nomas el examen de admisión). La mejor respuesta que te puedo dar, es depende… ¿De qué? Pues de muchas cosas;
- Depende de a quién le preguntes.
- De si estudiaste o no.
- De cuánto tiempo de queda para estudiar.
- De qué tanto dominas los temas básicos.
Guía Exani II contestada: Pensamiento matemático
Vamos a comenzar a resolver los reactivos de pensamiento matemático. Dado que son bastante, lo vamos a hacer en diferentes post, recuerda intentar resolverlos antes de ver la respuesta.
En el Nuevo Exani II únicamente se tienen tres respuestas por reactivo. Si quieres conocer todos los cambios no olvides revisar el mega post en donde te explicamos todo lo que tienes que saber sobre la nueva versión.
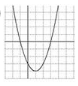
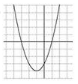
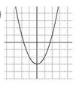
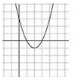
Reactivo 1: Función cuadrática
¿Cuál gráfica corresponde a la función f(x)=x^{2}-2 x-3 ?
Solución:
Ya que la función es un polinomio de segundo grado, su gráfica es la de una parábola con apertura paralela al eje y . Para determinar que grafica es la correcta, debemos determinar los puntos de corte con el eje x , de esa forma será fácil indicar la opción correcta.
Los puntos de corte.
Se iguala la función cuadrática a cero y se aplica la fórmula de segundo grado.
x^{2}-2 x-3=0
x_{1,2}=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}
Los valores de a, b \text { у } c son:
\begin{aligned} a &=1 \\ b &=-2 \\ c &=-3 \end{aligned}
Sustituimos y calculamos.
x_{1,2}=\frac{2 \pm \sqrt{4-4(1)(-3)}}{2}=\frac{2 \pm \sqrt{16}}{2}=\frac{2 \pm 4}{2}
x_{1}=\frac{2+4}{2}=3
x_{2}=\frac{2-4}{2}=-1
Ahora, solo debemos identificar cuál de las gráficas corta al eje x en -1 y 3. La gráfica del inciso a) cumple con esta característica, corta por la izquierda en -1 y por la derecha en 3, concluimos entonces que la respuesta correcta es la a).
Reactivo 2: Permutaciones
Angélica y sus 4 amigas dejan sus bicicletas en un bastidor que cuenta con 5 lugares. ¿De cuántas formas diferentes se pueden colocar las bicicletas?
- 5
- 25
- 120
- 3,125
Solución:
Para responder esta pregunta, debemos decidir qué técnica de conteo debemos emplear: permutaciones o combinaciones. La selección pasa por responder una simple pregunta ¿importa el orden en el que se coloquen las bicis en el bastidor?
Si lo pensamos por un momento, nos daremos cuenta de que sí. Cada combinación en la que Ana y sus amigas pueden colocar las bicis en el bastidor es diferente. En base a ello, debemos emplear permutaciones.
P_{n}^{m}=\frac{m !}{(m-n) !}
En este caso el número total de espacios es m=5 y la cantidad de ellos que se ocupan a la vez es n=4 .
P_{4}^{5}=\frac{5 !}{(5-4) !}=120
Ana y sus amigas pueden colocar las bicis de 120 formas diferentes. Comparando con las opciones, escogemos a c) como la respuesta correcta.
Reactivo 3: Ecuación de la Circunferencia
¿Cuál es la ecuación de una circunferencia con centro en el origen y radio igual a 3?
- x^{2}+y^{2}-3=0
- x^{2}+y^{2}-\sqrt{3}=0
- x^{2}+y^{2}-9=0
- x^{2}+y^{2}+9=0
Solución:
Para encontrar la ecuación general de la circunferencia, sustituimos las coordenadas del centro y el valor del radio en la ecuación ordinaria y luego la desarrollamos. El centro es el origen (h, k)=(0,0) y el radio es 3.
(x-h)^{2}+(y-k)^{2}=r^{2}
Sustituimos.
\begin{array}{l} x^{2}+y^{2}=3^{2} \\ x^{2}+y^{2}=9 \end{array}
Pasamos el término independiente al otro miembro para expresar la ecuación en su forma general.
x^{2}+y^{2}-9=0
Comparando con las ecuaciones mostradas en los incisos del problema, seleccionamos como respuesta correcta a la c).
Reactivo 4: Funciones trigonométricas
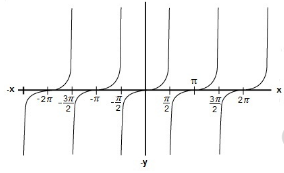
¿A qué función corresponde la gráfica?
- y=\tan (x)
- y=\tan (-x)
- y=\tan (2 x)
- y=\tan (-2 x)
Solución:
La gráfica de la función tiene claramente la forma de la identidad trigonométrica tangente. Ahora ¿Cómo la diferenciamos de las opciones que aparecen en los incisos?
Primero, no puede ser ninguna de las opciones con argumento negativo, sino la gráfica tendría que estar invertida respecto al eje y : apuntando a +\infty en -\frac{\pi}{2} y a -\infty \text { en } \frac{\pi}{2} . Segundo, no puede ser la del argumento doble porque si no en \frac{\pi}{2} valdría cero y no es así.
En base al análisis hecho, concluimos que la opción correcta es la a).
Reactivo 5: Ecuación de la recta
Juan hizo un recorrido en línea recta de la escuela ubicada en el punto (-3, -2) al auditorio que se encuentra en el punto (2, 4) ¿Cuál es la ecuación de la línea recta que se formó?
- 5 x-6 y-8=0
- 5 x+6 y-8=0
- 6 x-5 y+8=0
- 6 x+5 y+8=0
Solución:
Para encontrar la ecuación general de la recta, primero sustituimos en la ecuación punto pendiente un punto que pertenezca a la recta y el valor de la pendiente, para luego desarrollar y agrupar.
y-y_{o}=m\left(x-x_{o}\right)
La pendiente de la recta se calcula como:
m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}
Escogemos como P_{1}(-3,-2) \text { у а } P_{2}(2,4) .
m=\frac{4-(-2)}{2-(-3)}=\frac{6}{5}
Sustituimos el valor de la pendiente y al punto P_{1}(-3,-2) .
y+2=\frac{6}{5}(x+3)
Desarrollamos.
\begin{array}{c} 5 y+10=6 x+18 \\ -6 x+5 y-8=0 \\ 6 x-5 y+8=0 \end{array}
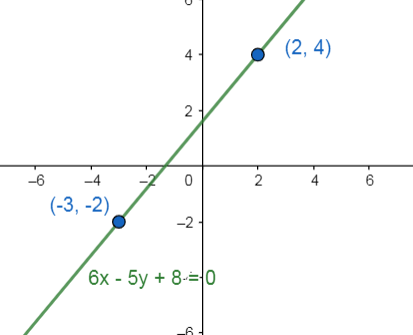
Seleccionamos como respuesta correcta a la opción c).
Reactivo 6: Factorización
La expresión \left(64 y^{2}-36\right) puede factorizarse como: [4(a y+b)(a y-b)] , donde los valores de a \text{ y } b son:
- a=-4, b=3
- a=4, b=9
- a=4, b=3
- a=8, b=6
Solución:
Para encontrar los valores correctos de los parámetros a \text { y } b , primero aplicamos diferencia de cuadrados, extraemos factor común 2 de ambos binomios y luego aplicamos igualación de polinomios para determinar sus valores.
Diferencia de cuadrados.
x^{2}-a^{2}=(x-a)(x+a)
Acomodamos el binomio del problema para aplicar la factorización.
\left(64 y^{2}-36\right)=\left(8^{2} y^{2}-6^{2}\right)=\left[(8 y)^{2}-6^{2}\right]
Factorizamos.
\left[(8 y)^{2}-6^{2}\right]=(8 y-6)(8 y+6)
Extraemos el factor común 4 de ambos binomios.
(8 y-6)(8 y+6)=2 \cdot(4 y-3) \cdot 2 \cdot(4 y+3)
Multiplicamos los coeficientes numéricos.
2 \cdot(4 y-3) \cdot 2 \cdot(4 y+6)=4(4 y-3)(4 y+3)
En base al resultado obtenido, para que sea igual a 4(a y+b)(a y-b), a \text { y } b deben ser:
a=4, b=3
Comparando con las opciones del problema, la respuesta correcta es la c).
Reactivo 7: Productos notables
El resultado de (-4 x+3 y)^{3} es:
- 64 x^{3}+27 y^{3}
- 64 x^{3}-144 x^{2} y+108 x y^{2}-27 y^{3}
- -64 x^{3}+27 y^{3}
- -64 x^{3}+144 x^{2} y-108 x y^{2}+27 y^{3}
Solución:
Para escoger la opción correcta, debemos aplicar el producto notable para un binomio elevado al cubo.
\begin{array}{l} (a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3} \\ (a-b)^{3}=a^{3}-3 a^{2} b+3 a b^{2}-b^{3} \end{array}
Ya que el primer término del binomio es negativo, podemos cambiarlo de lugar con el segundo gracias a la propiedad conmutativa de la suma, para aplicar la segunda fórmula del binomio cúbico.
(-4 x+3 y)^{3}=(3 y-4 x)^{3}
Desarrollamos.
(3 y-4 x)^{3}=27 y^{3}-3\left(9 y^{2}\right)(4 x)+3\left(16 x^{2}\right)(3 y)-64 x^{3}
Simplificamos productos.
(3 y-4 x)^{3}=27 y^{3}-108 x y^{2}+144 x^{2} y-64 x^{3}
Acomodamos los términos.
(3 y-4 x)^{3}=-64 x^{3}+144 x^{2} y-108 x y^{2}+27 y^{3}
Comparando con las opciones del problema, escogemos como correcta a la opción d).
Reactivo 8: Sustituir valores en la ecuación
Si D=\frac{3}{4} \text{ y } E=\frac{1}{3} , ¿Cuál es el resultado de \frac{1}{D-E} ?
- \frac{5}{12}
- \frac{12}{5}
- \frac{13}{12}
- \frac{12}{13}
Solución:
Sustituimos los valores de D \text { у } E en la expresión dada, resolvemos las operaciones con fracciones y concluimos con la respuesta correcta.
\frac{1}{D-E} \rightarrow \frac{1}{\frac{3}{4}-\frac{1}{3}}
Resta de fracciones.
\frac{1}{\frac{3}{4}-\frac{1}{3}}=\frac{1}{\frac{9-4}{12}}=\frac{1}{\frac{5}{12}}
División de fracciones
\frac{1}{\frac{5}{12}}=\frac{12}{5}
Comparando con las opciones del problema, escogemos como correcta a la b).
Reactivo 9: Simplificación algebraica
Elija la simplificación de la siguiente expresión:
m^{19} n^{19}\left(\frac{1}{m}\right)^{30}\left(\frac{1}{n}\right)^{30}
- m^{11} n^{11}
- m^{45} n^{45}
- \frac{900}{m^{11} n^{11}}
- \frac{1}{m^{11} n^{11}}
Solución:
Para encontrar la forma simplificada de la expresión dada, debemos aplicar las propiedades de los exponentes para producto y el cociente de potencias con igual base. Primero, distribuimos el exponente de las fracciones.
m^{19} n^{19}\left(\frac{1}{m}\right)^{30}\left(\frac{1}{n}\right)^{30}=m^{19} n^{19} \frac{1}{m^{30}} \frac{1}{n^{30}}
Acomodamos los factores, de modo que se encuentren los que poseen igual base en la misma fracción.
m^{19} n^{19} \frac{1}{m^{30}} \frac{1}{n^{30}}=\frac{m^{19}}{m^{30}} \frac{n^{19}}{n^{30}}
Aplicamos la propiedad de cociente de potencias con igual base.
\frac{m^{19}}{m^{30}} \frac{n^{19}}{n^{30}}=m^{19-30} n^{19-30}=m^{-11} n^{-11}
Por último, se expresa el resultado en forma de fracción empleando la propiedad del exponente negativo.
m^{-11} n^{-11}=\frac{1}{m^{11} n^{11}}
Comparando la expresión resultante con las opciones de los incisos, seleccionamos como respuesta correcta la d).
Reactivo 10: La circunferencia
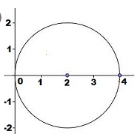
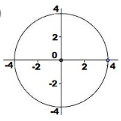
¿Cuál es la gráfica que corresponde a la ecuación x^{2}+y^{2}=16 ?
Solución:
Para escoger la gráfica correcta, debemos identificar el centro y el radio de la circunferencia. La ecuación dada está en la forma ordinaria de la circunferencia por tanto, podemos extraer de forma directa el centro y el radio.
(x-h)+(y-k)=r^{2} \rightarrow x^{2}+y^{2}=16
El centro es el origen de coordenadas C(0,0) y el radio r^{2}=16 \rightarrow r=4 .
La circunferencia está centrada en el origen, intersecta al eje x y al eje y en 4 y -4. Comparando este análisis con las gráficas de los incisos, escogemos como respuesta correcta a la opción b).