Guía EXANI II | Módulo de Matemáticas Reactivos del 1 al 22 resueltos

¡Hola, joven aspirante! Si estás por aplicar a alguna universidad donde se realiza el Exani II, seguramente entiendes lo importante que es prepararse para este. Por ello, hemos preparado esta guía, en la cual te ayudaremos a estudiar para el Módulo Matemáticas. Este es uno de los módulos módulos específicos más desafiantes del examen, así que dale la importancia que amerita.

Aquí te apuntamos algunos detalles importantes referentes al Exani II:

Desde el verano de este año 2021, el Exani sufrió una serie de cambios implementados por Ceneval, organismo responsable de esta prueba. En vista de ello, puede que sea de mucha ayuda que conozcas algunos de estos cambios y cómo es la estructura del nuevo Exani II:

[wpipa id=»10740″]

No olvides que el Exani II es una prueba dirigida por Ceneval, un organismo independiente encargado de llevar a cabo este examen en varias de las universidades más importantes de México.

Estructura del Exani II

Ya casi damos inicio a nuestra guía resuelta de reactivos de Matemáticas de la guía del Exani II. Pero antes, acá te mostramos la estructura del examen.

Mira la siguiente tabla y toma nota:

Área	Reactivos
Habilidades y conocimientos
Pensamiento matemático	30
Comprensión lectora	30
Redacción indirecta	30
Módulos de conocimientos específicos
Módulo 1	24
Módulo 2	24
Subtotal de reactivos	138
Diagnóstico
Inglés	30
Total de reactivos	168

Tabla Estructura Exani II

Como te hemos explicado hace minutos, durante este año, Ceneval aplicó una serie de cambios al Exani. La mayoría de ellos consistieron en eliminar módulos de conocimiento que se consideraban innecesarios y, en su lugar, se añadieron otros nuevos en sustitución.

Ahora bien, para conocer a detalle cuáles fueron estos cambios y cómo es la estructura del Exani, acá tienes un post informativo donde te dejamos todo lo que necesitas saber:

Estructura Exani II

Temario Matemáticas

Estamos por iniciar los reactivos referentes al módulo de Matemáticas de la guía del Exani II. Sin embargo, antes te mostraremos el temario que Ceneval ha publicado para esta área de conocimiento.

Las matemáticas se abordan en un Módulo específico del Exani II de Ceneval.

Acá tienes una tabla con los detalles del temario de Matemáticas:

¿Qué tan difícil es el módulo de Matemáticas del Exani II?

Una pregunta que siempre suele escucharse antes de las fechas de un examen, es referente a qué tan difícil es. Esto también es común entre las personas que están por presentar el Exani II. Si tú tienes esta inquietud, queremos que sepas que la respuesta te la puedes dar tú mismo en base a tres interrogantes clave:

• ¿Le has dedicado tiempo a estudiar y prepararte para el examen?
• ¿Estás familiarizado con los módulos y temas del examen?
• ¿Dominas y conoces lo necesario para desenvolverte en los aspectos más importantes de la evaluación?

Guía Exani II contestada: Matemáticas

Ya casi empezamos con los ejercicios resueltos en matemáticas del Exani II de Ceneval. En este caso, debido a que son 22 reactivos, vamos a mostrártelos todos en esta misma guía. Ten en cuenta que para estudiar, lo mejor es que intentes resolverlos tú mismo antes de ver la respuesta en esta guía.

ten en cuenta que debido al nuevo formato del Exani, ahora las respuestas de selección múltiple plantean tres opciones distintas. Si quieres saber más detalles respecto a la estructura de esta prueba, aquí tienes nuestro post donde no pasamos nada por alto y te lo contamos todo:

 Guía Exani II

Reactivo 1: Notación Científica

¿Cuál es el valor de la expresión?

\frac{\left(5 \times 10^{-3}\right)\left(6 \times 10^{6}\right)}{15 \times 10^{-6}}

1. \frac{11}{5} \times 10^{-3}
2. 2 \times 10^{-9}
3. 2 \times 10^{-24}
4. 2 \times 10^{9}

Solución:

Para resolver productos y cocientes entre cantidades representadas en notación científica, se aplican propiedades de los exponentes a las potencias de base 10 y se multiplican o dividen entre ellos a los números que se encuentran frente a las potencias de base 10.

\frac{\left(5 \times 10^{-3}\right)\left(6 \times 10^{6}\right)}{15 \times 10^{-6}}

Multiplicamos las cantidades en el numerador. Se aplica el producto de potencias de igual base y se multiplica el 5 con el 6.

\frac{\left(5 \times 10^{-3}\right)\left(6 \times 10^{6}\right)}{15 \times 10^{-6}}=\frac{30 \times 10^{-3+6}}{15 \times 10^{-6}}=\frac{30 \times 10^{3}}{15 \times 10^{-6}}

Ahora, se aplica el cociente de potencias de igual base y se divide el 30 con el 15.

\frac{30 \times 10^{3}}{15 \times 10^{-6}}=2 \times 10^{3-(-6)}=2 \times 10^{9}

Comparando el resultado obtenido con las opciones en los incisos, seleccionamos como respuesta correcta a la d).

Reactivo 2: Convertir decimal en fracción

¿Qué fracción representa el número decimal 0.625?

1. \frac{625}{10,000}
2. \frac{625}{1.000}
3. \frac{625}{100}
4. \frac{625}{10}

Solución:

Primero, identificamos si la cantidad decimal es finita o periódica. En nuestro caso, posee decimales finitos por tanto, para expresarlo en fracción se corre la coma hacia la derecha hasta que ya no existan cifras decimales.

0.625 \rightarrow 625

Se corrió la coma a la derecha 3 veces.

Ahora, se divide el número obtenido por un 1 seguido de tantos ceros como corrimientos de coma se dieron en el paso anterior. Ya que se corrió la coma 3 veces, se divide por 1000.

0.625=\frac{625}{1000}

Por último, de ser posible se simplifica la fracción. Como las opciones del problema no se dan de forma simplificada, omitimos este paso por esta vez. Comparando con las opciones, escogemos como respuesta correcta a la b).

Reactivo 3: Factorización de polinomios

Factorice el siguiente polinomio:

6 x^{2}-5 x-6=0

1. (2 x-3)(3 x+2)=0
2. (2 x+3)(3 x-2)=0
3. (-2 x-3)(-3 x+2)=0
4. (3 x-3)(2 x-2)=0

Solución:

Para factorizar un trinomio al cuadrado con a>1 , se multiplica toda la expresión por a y se factoriza el trinomio cuadrado tomando a x como variable. Ya que a=6 obtenemos que:

6\left(6 x^{2}-5 x-6\right)=0

(6 x)^{2}-5(6 x)-36=0

Buscamos dos números que sumados den -5 y multiplicados -36. En este caso son: -9 y 4.

-9+4=-5

(-9)(4)=-36

Escribimos el polinomio en la forma factorizada (a x+c)(a x+b) .

(6 x-9)(6 x+4)=0

Extraemos factor común en ambos binomios y simplificamos.

3(2 x-3) 2(3 x+2)=0

(2 x-3)(3 x+2)=0

Comparando con las opciones del problema, escogemos como respuesta correcta a la a).

Reactivo 4: Simplificación de expresiones racionales

¿Cuál es la simplificación mínima de la expresión racional?

\frac{2 x^{2}+13 x+15}{6 x^{2}+7 x-3}

1. \frac{(2 x+3)(x+5)}{(3 x+1)(2 x-3)}
2. \frac{3 x-1}{x+5}
3. \frac{x+5}{3 x-1}
4. \frac{(2 x-3)(x-5)}{(3 x-1)(2 x+3)}

Solución:

La simplificación de expresiones racionales pasa por factorizar los polinomios tanto en el numerador como en el denominador y luego se simplifican los factores comunes.

Factorizamos el numerador.

\frac{1}{2} \frac{(2 x)^{2}+13(2 x)+30}{6 x^{2}+7 x-3}

Encontramos dos números que multiplicados den 30 y sumados 13, en este caso son 3 y 10.

\frac{1}{2} \frac{(2 x)^{2}+13(2 x)+30}{6 x^{2}+7 x-3}=\frac{1}{2} \frac{(2 x+10)(2 x+3)}{6 x^{2}+7 x-3}

Factorizamos el denominador.

\frac{6}{2} \frac{(2 x+10)(2 x+3)}{(6 x)^{2}+7(6 x)-18}=3 \frac{(2 x+10)(2 x+3)}{(6 x)^{2}+7(6 x)-18}

Encontramos dos números que sumados den 7 y multiplicados -18, en este caso son 9 y -2.

3 \frac{(2 x+10)(2 x+3)}{(6 x+9)(6 x-2)}

Extraemos factor común de (6 x+9) al 3.

3 \frac{(2 x+10)(2 x+3)}{3(2 x+3)(6 x-2)}

Simplificamos.

3 \frac{(2 x+10)(2 x+3)}{3(2 x+3)(6 x-2)}=\frac{(2 x+10)}{(6 x-2)}

Por último, extraemos factor común 2 en ambos binomios y simplificamos.

\frac{x+5}{3 x-1}

Comparando con las opciones de cada inciso, escogemos como respuesta correcta a la c).

Reactivo 5: Producto entre polinomios

Dadas las funciones f(x)=3 x^{2}-x^{3} \text{ y } g(x)=3 x^{2}+5 x^{3} , el producto entre ellas es igual a…

1. 9 x^{4}+12 x^{6}-5 x^{9}
2. 9 x^{4}+7 x^{6}
3. 9 x^{4}+12 x^{5}-5 x^{6}
4. 3 x^{4}+18 x^{5}+5 x^{6}

Solución:

El producto entre dos polinomios se efectúa multiplicando cada uno de los términos del primero con el segundo polinomio, luego efectuando las distributivas respectivas y por último simplificando la expresión resultante.

f(x) \cdot g(x)=\left(3 x^{2}-x^{3}\right)\left(3 x^{2}+5 x^{3}\right)

Efectuamos el producto término a término de 3 x^{2}-x^{3} con 3 x^{2}+5 x^{3} .

f(x) \cdot g(x)=3 x^{2}\left(3 x^{2}+5 x^{3}\right)-x^{3}\left(3 x^{2}+5 x^{3}\right)

Efectuamos las distributivas.

f(x) \cdot g(x)=9 x^{4}+15 x^{5}-3 x^{5}-5 x^{6}

Agrupamos y simplificamos.

f(x) \cdot g(x)=9 x^{4}+12 x^{5}-5 x^{6}

Examinando las opciones del problema, escogemos como respuesta correcta a la c).

Reactivo 6: Propiedades de los exponentes

Exprese en forma de potencia la siguiente expresión matemática.

\sqrt[3]{x^{5}}

1. \sqrt[3]{x^{5}}
2. x^{15}
3. x^{\frac{5}{3}}
4. x^{\frac{3}{5}}

Solución:

En este caso, debemos emplear la propiedad del exponente racional:

\sqrt[m]{a^{n}}=a^{\frac{n}{m}}

Es decir, la potencia pasa a ser el numerador y el índice de la raíz el denominador del exponente racional. Para nosotros n=5 \text { y } m=3 , por tanto:

\sqrt[3]{x^{5}}=x^{\frac{5}{3}}

Luego de comparar nuestro resultado, escogemos como correcta a la opción c).

Reactivo 7: Perímetro de figuras planas

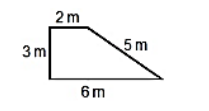
Se requiere construir una barda alrededor de un huerto. Considerando los datos de la imagen, ¿cuántos metros se necesitan construir?

1. 8
2. 12
3. 14
4. 16

Solución:

Los metros de material que se necesitan para construir la barda, se obtienen de calcular el perímetro del huerto. Ya que tenemos la longitud de cada uno de los lados del huerto, el perímetro lo encontramos como la suma de todos sus lados:

P_{h}=2+5+3+6=16 m

Concluimos que se necesitan construir 16 metros de barda para cubrir el perímetro total del huerto. La respuesta correcta al problema es la opción d).

Reactivo 8: Radio de un cilindro

¿Cuál es el radio de la base de un cilindro cuyo volumen es 197.92 cm3 y su altura es de 7 cm?

1. 3 cm
2. 85 cm
3. 6 cm
4. 27 cm

Solución:

El volumen de un cilindro se calcula como el área de su base multiplicada por la altura:

V_{c}=\pi r^{2} h

De esta fórmula, despejamos y calculamos el radio que debe tener la base del cilindro.

r=\sqrt{\frac{V_{c}}{\pi h}}

Sustituimos.

r=\sqrt{\frac{197.92 \mathrm{~cm}^{3}}{\pi(7 \mathrm{~cm})}}=2.9999 \mathrm{~cm}=3 \mathrm{~cm}

Concluimos que el radio de la base es igual a 3 cm. Comparando con las opciones, escogemos como respuesta correcta a la a).

Reactivo 9: Prisma de base cuadrada

Un prisma tiene una base cuadrada, altura de 12 cm y volumen de 108 cm3, ¿cuál es el perímetro de la base?

1. 3 cm
2. 9 cm
3. 12 cm
4. 27 cm

Solución:

El volumen de un prisma con base cuadrada, se calcula multiplicando el área de la base por la altura. Como el prisma tiene base cuadrada, el are de su base es A_{b}=a^{2} por tanto:

V_{p}=a^{2} h

El problema solicita que calculemos el perímetro de la base, por tanto una vez calculado a (que es la longitud de los lados de la base cuadrada) el perímetro se obtiene como:

P_{b c}=4 a

Despejamos de la ecuación de volumen a .

a=\sqrt{\frac{V_{p}}{h}}

Sustituyendo.

a=\sqrt{\frac{108 \mathrm{~cm}^{3}}{12 \mathrm{~cm}}}=3 \mathrm{~cm}

Por último, el perímetro de la base es:

P_{b c}=4(3 \mathrm{~cm})=12 \mathrm{~cm}

Concluimos entonces que la base del prisma tiene 12 cm de perímetro, por tanto la respuesta correcta es la opción c).

Reactivo 10: Pendiente de un plano inclinado

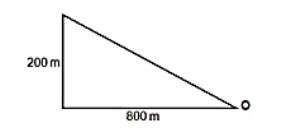
El tramo de una carretera está inclinado como se muestra en la imagen. ¿Cuánto vale su pendiente si el origen está en el punto O?

1. -4
2. -1/4
3. 5/4
4. 2

Solución:

Como sabemos, la pendiente de cualquier recta en el plano cartesiano de calcula como:

m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}

En nuestro caso, el origen es O y representa al extremo inicial del plano inclinado. Por otra parte, el extremo final del plano es 800m a la izquierda y 200m hacia arriba o (-800,200) expresado como un punto en el plano.

Sustituimos los extremos en la ecuación y calculamos el valor de la pendiente:

m=\frac{200-0}{-800-0}=-\frac{1}{4}

Concluimos que la pendiente del plano inclinado es negativa y vale -\frac{1}{4} . Otra forma de comprobar el signo, es que toda recta entre el segundo y tercer cuadrante tiene una pendiente negativa. Escogemos como respuesta correcta la opción b).

Reactivo 11: Pendiente de la recta

¿Cuál es el valor de la pendiente de la recta en la ecuación?

6 x-3 y+12=0

1. -3
2. 2
3. 4
4. 6

Solución:

La ecuación de la recta en este caso se encuentra en la forma general, por tanto la pendiente la podemos calcular como:

m=-\frac{A}{B}

Donde:

A x+B y+C=0

En nuestro caso, el coeficiente A=6 y el B=-3 , sustituimos estos valores en la fórmula de la pendiente:

m=-\frac{6}{-3}=-(-2)=2

La pendiente de la recta que tiene como ecuación 6 x-3 y+12=0 \text { es } m=2 . Escogemos como respuesta correcta a la opción b). Otra forma de encontrar el valor de la pendiente es despejando a la variable y .

6 x-3 y+12=0 \rightarrow y=2 x+4

La pendiente es el coeficiente que acompaña a x , es decir 2.

Reactivo 12: Ecuación de la recta

¿Cuál es la ecuación de la recta que pasa por el punto (-2, 1) y tiene pendiente de 3?

1. y=3 x-5
2. y=3 x+3
3. y=3 x+5
4. y=3 x+7

Solución:

En este caso, empleamos la ecuación punto-pendiente de la recta ya que el problema nos facilita la pendiente y un punto que pertenece a la recta.

y-y_{o}=m\left(x-x_{o}\right)

Donde:

• \left(x_{o}, y_{o}\right)=(-2,1)
• m=3

Sustituimos en la ecuación.

y-1=3(x+2)

Desarrollamos y simplificamos.

y=3 x+7

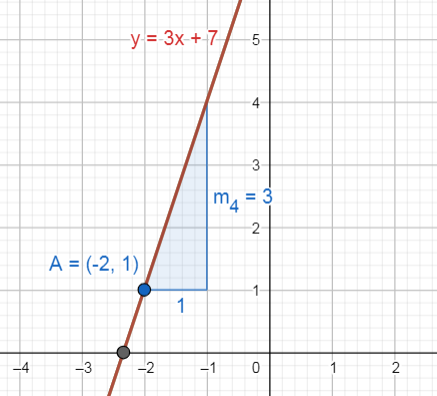
Escogemos como respuesta correcta a la opción d).

Reactivo 13: Pendiente

¿Cuál es la pendiente de la función lineal a la que pertenecen los puntos de la tabla?

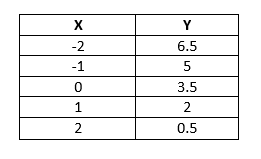
1. m=-\frac{3}{2}
2. m=-\frac{2}{3}
3. m=\frac{17}{12}
4. m=\frac{9}{2}

Solución:

Aunque el enunciado del problema indica que la función es lineal, debemos asegurarnos de que esto sea así. Para ello comprobamos que los números en ambas columnas incrementen de forma constante.

En la columna de la izquierda los números incrementan de 1 en 1, mientras que en la derecha los datos disminuyen de 1.5 en 1.5. Comprobada la linealidad, calculamos la pendiente como:

m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}

Escogemos como P_{1}(0,3.5) \text { y } P_{2}(1,2) . Sustituimos y calculamos:

m=\frac{2-3.5}{1-0}=-1.5

Resultado que puede escribirse como m=-\frac{3}{2} .

Comparando con las opciones, la respuesta correcta es la a).

Reactivo 14: Dominio de funciones reales

¿Cuál es el dominio de la función?

\sqrt{4-9 x}

1. \left(-\infty, \frac{4}{9}\right)
2. \left(-\infty, \frac{4}{9}\right]
3. \left[-\frac{4}{9},-\infty\right)
4. (-\infty, \infty)

Solución:

El dominio de una función son todos los valores que pueden ingresar a la función para obtener un resultado finito y en los reales. Como nuestra función es radical, la única condición que tenemos es que el radicando sea mayor o igual que cero, es decir:

4-9 x \geq 0

Despejamos el conjunto solución de la inecuación lineal.

-9 x \geq-4

9 x \leq 4

x \leq \frac{4}{9}

Expresado en notación de conjunto:

\forall x \in\left(-\infty, \frac{4}{9}\right]

Comparando con las opciones, la respuesta correcta es la b).

Reactivo 15: Rango de una función real

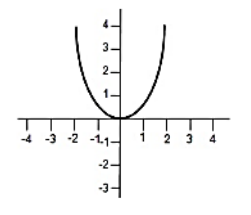
¿Cuál es la imagen de la función cuadrática de la gráfica?

1. (0, \infty)
2. (-\infty, 0)
3. [0, \infty)
4. (-\infty, \infty)

Solución:

La imagen o rango de una función real son todos los valores que se obtienen a partir del dominio de la función, es decir el conjunto de resultados que se obtienen al sustituir uno a uno los valores del dominio.

En nuestro caso, no tenemos a la función en forma de ecuación sino una representación gráfica de ella. Fácilmente podemos identificar que se trata de una parábola cuyo vértice es el origen y abre hacia las y positivas.

Con todo esto, podemos asegurar que el rango de la función va desde 0 hasta +\infty . Escrito en notación de conjunto quedaría como:

\forall x \in[0,+\infty)

Escogemos como respuesta correcta a la opción c).

Reactivo 16: Elementos de un triángulo

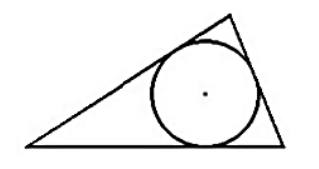
Con base en la figura, para encontrar el centro de la circunferencia tendrá que determinarse el punto de intersección de dos de sus…

1. Medianas
2. Mediatrices
3. Alturas
4. Bisectriz

Solución:

De los temas referentes a trigonometría, sabemos que el incentro de un triángulo es el centro de una circunferencia interna que es tangente a sus lados en un punto, dicha situación es la que se presenta en la imagen.

El incentro, se puede encontrar al intersectar dos de las bisectrices de los ángulos formados por los ángulos internos al triángulo. En base al análisis hecho, podemos concluir que la respuesta correcta es la opción d).

Reactivo 17: Producto notable

¿Cuál es el resultado de elevar \left(4 p^{3} q^{4}-4\right) al cuadrado?

1. 4 p^{6} q^{8}-6 p^{3} q^{4}+8
2. 8 p^{6} q^{8}-12 p^{3} q^{4}+16
3. 16 p^{6} q^{8}-32 p^{3} q^{4}+16
4. 16 p^{6} q^{8}-24 p^{3} q^{4}+32

Solución:

Para calcular el cuadrado de la expresión dada, podemos recurrir al uso de los productos notables, más en específico al producto notable del cuadrado del binomio de la diferencia de dos números:

(a-b)^{2}=a^{2}-2 a b+b^{2}

En este caso a es el término 4 p^{3} q^{4} y b es 4. Aplicando el desarrollo nos queda:

\left(4 p^{3} q^{4}-4\right)^{2}=\left(4 p^{3} q^{4}\right)^{2}-2\left(4 p^{3} q^{4}\right)(4)+16

Simplificamos las potencias y productos restantes.

\left(4 p^{3} q^{4}-4\right)^{2}=16 p^{6} q^{8}-32 p^{3} q^{4}+16

Comparando el resultado obtenido con las opciones del problema, escogemos como respuesta correcta a la c).

Reactivo 18: Límites

¿Cuál es el resultado del \operatorname{Lim}_{h \rightarrow 0}[x+h]^{w} ?

1. 0
2. h^{w}
3. x^{w}
4. w

Solución:

Para resolver cualquier límite, el primer paso es evaluar el número al que tiende la variable, en este caso h \rightarrow 0 , en la función e identificar si el resultado es finito, no existe o se presenta una indeterminación.

Evaluamos.

\operatorname{Lim}_{h \rightarrow 0}[x+h]^{w}=[x+0]^{w}=x^{w}

Esta vez, el límite de [x+h]^{w} cuando h tiende a cero es x^{w} . Concluimos entonces que la respuesta correcta es la opción c).

Reactivo 19: Derivada de una función

¿Cuál es la derivada de f(x)=\ln (2 x+1) ?

1. \frac{2 x+1}{2}
2. \frac{2}{x+1}
3. \frac{2}{2 x+1}
4. \frac{1}{2 x+1}

Solución:

Primero, debemos identificar qué tipo de función es o si hay presentes suma o producto entre funciones para seleccionar la fórmula de derivación correcta. En este caso, es la función logaritmo natural que tiene como fórmula de derivación:

\frac{d[\ln \ln f(x)]}{d x}=\frac{f(x)^{\prime}}{f(x)}

Es decir, la derivada es igual a la derivada del argumento del logaritmo sobre el argumento del logaritmo sin derivar. Aplicándolo a la función dada nos queda que:

\frac{d[\ln (2 x+1)]}{d x}=\frac{(2 x+1)^{\prime}}{2 x+1}

Ahora, aplicamos la propiedad de la derivada de una suma y luego las fórmulas de la derivada de x por una constante y la derivada de una constante.

\frac{d[\ln (2 x+1)]}{d x}=\frac{(2 x+1)^{\prime}}{2 x+1}=\frac{(2 x)^{\prime}+(1)^{\prime}}{2 x+1}

\frac{d[\ln (2 x+1)]}{d x}=\frac{2+0}{2 x+1}=\frac{2}{2 x+1}

Concluimos entonces que la derivada de \ln (2 x+1) \text { es } \frac{2}{2 x+1} .

Comparando con las opciones, la respuesta correcta es la opción c).

Reactivo 20: Derivada de una función

La derivada de la función f(x)=3 x^{5} es:

1. 3 x^{4}
2. 15 x^{4}
3. 15 x^{-4}
4. 15 / x^{4}

Solución:

En este caso, la fórmula de derivación que debemos aplicar es la de una función elevada a una potencia:

\frac{d\left[f(x)^{n}\right]}{d x}=n \cdot f(x)^{\prime} \cdot f(x)^{n-1}

Aplicada a nuestro caso quedaría:

\frac{d\left[3 x^{5}\right]}{d x}=3 \frac{d\left[x^{5}\right]}{d x}=3 \cdot 5 \cdot(x)^{\prime} \cdot x^{4}

Simplificando.

\frac{d\left[3 x^{5}\right]}{d x}=15 x^{4}

Comparando con las opciones, la respuesta correcta es la b).

Reactivo 21: Integral definida

¿Cuál es el resultado de la integral?

\int_{-1}^{2} 3 x^{2}+2 x-1 d x

1. -9
2. 1
3. 9
4. 15

Solución:

Para calcular la integral definida, primero debemos integrar de forma indefinida a la función integrando, en este caso f(x)=3 x^{2}+2 x-1 y luego evaluar el resultado F(x) entre los límites de integración i=F(b)-F(a) .

Primero, aplicamos la propiedad de la integral de una suma:

\int_{-1}^{2} 3 x^{2}+2 x-1 d x=\int_{-1}^{2} 3 x^{2} d x+\int_{-1}^{2} 2 x d x-\int_{-1}^{2} d x

Ahora, aplicamos la fórmula de la integral de una potencia y la integral del diferencial.

\int_{-1}^{2} 3 x^{2} d x+\int_{-1}^{2} 2 x d x-\int_{-1}^{2} d x=\frac{3 x^{3}}{3}\left|\frac{2}{-1}+\frac{2 x^{2}}{2}\right| \frac{2}{-1}-x \mid \frac{2}{-1}

Simplificamos y evaluamos.

\frac{3 x^{3}}{3}\left|\frac{2}{-1}+\frac{2 x^{2}}{2}\right| \frac{2}{-1}-x\left|\frac{2}{-1}=x^{3}\right| \frac{2}{-1}+x^{2}\left|\frac{2}{-1}-x\right| \frac{2}{-1}

(2)^{3}-(-1)^{3}+(2)^{2}-(-1)^{2}-[2+1]=9+3-3

Concluimos que:

\int_{-1}^{2} 3 x^{2}+2 x-1 d x=9

Comparando con las opciones, la respuesta correcta es la c).

Reactivo 22: Integral indefinida

La solución de la integral está dada por…

\int \frac{d x}{\sqrt{a-b x}}

1. -\frac{\sqrt{a-b x}}{2 b}
2. -\frac{2 \sqrt{a-b x}}{b}
3. \frac{2 \sqrt{a-b x}}{b}
4. \frac{2 \sqrt{a+b x}}{b}

Solución:

Para resolver esta integral, debemos aplicar sustitución. En este caso, la sustitución se le debe aplicar al argumento del radical es decir a a-b x . El cambio quedaría como:

z=a-b x

d z=-b d x \rightarrow d x=-\frac{1}{b} d z

Aplicamos la sustitución en la integral.

-\frac{1}{b} \int \frac{d z}{\sqrt{z}}

Expresamos al radical como un número elevado a una potencia fraccionaria negativa.

-\frac{1}{b} \int \frac{d z}{\sqrt{z}}=-\frac{1}{b} \int z^{-\frac{1}{2}} d z

Aplicamos la fórmula de la integral de una potencia.

-\frac{1}{b} \int z^{-\frac{1}{2}} d z=-\frac{1}{b} \frac{z^{1-\frac{1}{2}}}{1-\frac{1}{2}}+c=-\frac{2 \sqrt{z}}{b}+c

Devolvemos el cambio de variables.

z=a-b x

\int \frac{d x}{\sqrt{a-b x}}=-\frac{2 \sqrt{a-b x}}{b}+c

Comparando con las opciones del problema, la respuesta correcta es la b).