¡Hola aspirante! En este tutorial vamos a resolver los 30 primeros ejercicios del simulacro de Física correspondiente al módulo 9 del examen de conocimientos específicos de cara a la nueva prueba EXANI diseñada por Ceneval.

Aquí tienes algunos detalles importantes sobre Exani II:
- Desarrollo: Ceneval
- Examen de admisión: Exani II
- Reactivos: 168
- Tipo: Opción múltiple
- Duración: 4 horas y media
- Modalidades: Presencial, en línea y desde casa.
Recuerda que este es un simulacro hecho para que practiques con ejercicios similares a los del examen. No mires las respuestas antes de resolverlos, es importante que domines cada uno de los temas y que practiques para afianzar los conceptos.
Estructura del Exani II
Para este año 2022, la prueba EXANI consta de dos grandes partes: la primera, sobre conocimientos generales, denominada habilidades y conocimientos y la segunda, que cubre los temas de conocimientos específicos que varían de acuerdo a tu carrera.
La sección de conocimientos generales está compuesta por 30 reactivos de matemáticas y otros 60 de español, divididos entre comprensión lectora y redacción indirecta.
También existe un examen diagnóstico de inglés, pero la aplicación del mismo depende de la Universidad y no tiene repercusión en tu puntaje final.
Esta tabla contiene un resumen conciso de la estructura que tendrá el examen real.
Conoce la estructura de la guía Exani II y del examen de ingreso
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Examen conocimientos específicos
El nuevo Exani II de ceneval se divide en dos partes, que son las que cuentan para tu resultado final, la primera corresponde al examen de conocimiento y habilidades, y la segunda a la prueba de conocimientos específicos.
En el caso del módulo 9 correspondiente a física suele aplicarse a carreras de ciencias e ingenierías, aunque recuerda que la decisión de que modulo aplicada cada carrera depende 100 % de tu universidad.
Estos son los 16 módulos de conocimientos específicos
| 1. Administración | 9. Física |
| 2. Aritmética | 10. Historia |
| 3. Biología | 11. Literatura |
| 4. Cálculo diferencial e integral | 12. Matemáticas financieras |
| 5. Ciencias de la Salud | 13. Premedicina |
| 6. Derecho | 14. Probabilidad y estadística |
| 7. Economía | 15. Química |
| 8. Filosofía | 16. Psicología |
Temario de Física
Los reactivos de física en la prueba EXANI se encuentran en la parte de conocimientos específicos, dicha parte contiene 2 módulos con asignaturas relacionadas con la carrera a la que aspiras. Debes revisar en tu universidad cuáles son los módulos que presentarás.
Estos 50 ejercicios se encuentran distribuidos entre los siguientes temas de física:
| Subárea | Reactivos |
|---|---|
| Mecánica | 10 |
| Óptica, ondas y electromagnetismo | 14 |
| Total | 24 |
Subárea: Mecánica
- Sistemas de fuerzas coplanares concurrentes y distribuidos
- Elementos que intervienen en el movimiento circular uniforme
- Cálculo de fuerza centrípeta
- Variables relacionadas con el trabajo rotacional y la energía cinética rotacional
- Conservación del momento angular
- Ley de la conservación de la cantidad de movimiento
- Tipos de choque y variables relacionadas
Subárea: Óptica, ondas y electromagnetismo
- Sistemas de objetos que interactúan a través de sus campos magnéticos
- Generación de fuerza magnética
- Sistemas de fuerzas entre corrientes
- Sistemas conductores que generan campos magnéticos
- Tipos y variables que intervienen en el movimiento armónico simple
- Clasificación, componentes y representación gráfica de ondas
- Aplicación tecnológica de fenómenos ondulatorios
- Tipos de lente
- Características y parámetros que intervienen en los fenómenos ópticos
Puedes estudiar cada uno de estos temas desde la bibliografía recomendada en la guía oficial de EXANI. No dejes ningún tema sin cubrir y dedica tiempo a comprender los conceptos, física es una asignatura que depende enormemente de comprender la teoría.
¿Cómo resolver el examen simulacro?
Estos ejercicios simulacro tienen como finalidad ayudarte en dos aspectos: practicar los temas que van para el examen real y trabajar en el tiempo que tardas en resolverlos.
Debe incluir exámenes simulacro en tu calendario de estudios, así pondrás en práctica tus conocimientos en condiciones similares a las del examen.
Las siguientes son algunas recomendaciones que puedes seguir mientras estudias con este simulacro.
- Resuelve completa cada parte por tu cuenta antes de mirar las respuestas
- Establece un tiempo no mayor a 20 minutos por cada 10 reactivos
- Analiza el procedimiento que has seguido para resolver los ejercicios y piensa en posibles alternativas que acorten el tiempo
- Asegúrate de tener unos minutos de sobra para comprobar tus respuestas
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico
Ejercicios de Física
Luego de esta introducción, vamos con la solución paso a paso de los primeros 10 reactivos tipo selección múltiple del simulacro de Física, inspirados en el examen real de Ceneval Exani.
Reactivo 1
Dado el sistema de fuerzas mostrado a continuación, determine el coeficiente de fricción estático entre el bloque de masa m y la rampa para que se cumpla la condición de equilibrio. Trabaje en forma algebraica su respuesta.
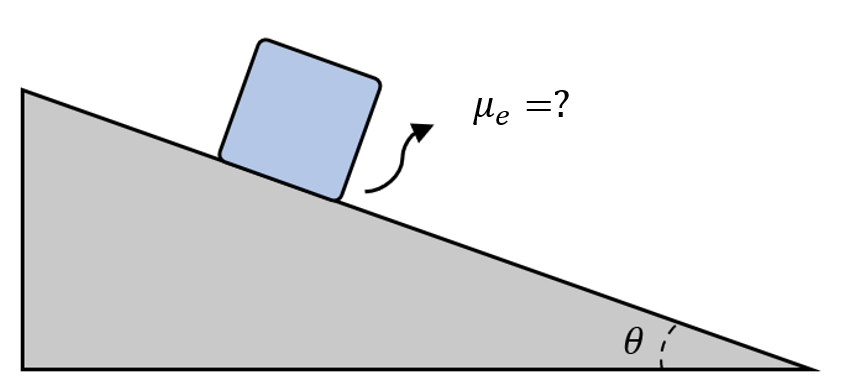
- {\mu }_{e}=\mathrm{sin}\theta
- {\mu }_{e}=\mathrm{cos}\theta
- {\mu }_{e}=\mathrm{tan}\theta
Solución:
Para calcular el valor que debe tener el coeficiente de roce estático entre la masa y la rampa, debemos iniciar identificando el DCL del sistema.
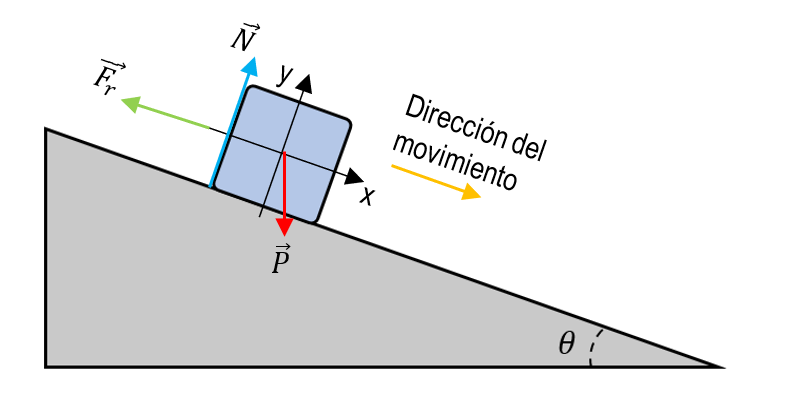
Trasladando los vectores de fuerza de rozamiento (en sentido opuesto a la dirección del movimiento), el peso y la normal, a un plano cartesiano el sistema quedaría representado como:
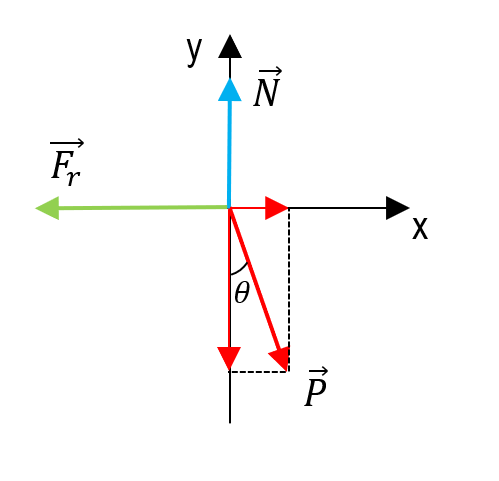
Aplicando la definición de la primera condición de equilibrio del movimiento:
\sum {F}_{x}=0
\sum {F}_{y}=0
Obtenemos el siguiente SE.
\sum {F}_{x}:{P}_{x}-{F}_{r}=0
\sum {F}_{y}:N-{P}_{y}=0
A partir del DCL, sabemos que las componentes del peso quedan de la siguiente forma:
{P}_{x}=P\mathrm{sin}\theta , {P}_{y}=P\mathrm{cos}\theta
Si P=mg , sustituimos en las ecuaciones de equilibrio para obtener:
\left\{\begin{array}{c}mg\mathrm{sin}\theta -{F}_{r}=0\\ N-mg\mathrm{cos}\theta =0\end{array}\right.
Además, la fuerza de roce estática por definición es:
{F}_{r}={\mu }_{e}N
De la segunda ecuación despejamos la magnitud de la normal.
N=mg\mathrm{cos}\theta
\therefore {F}_{r}={\mu }_{e}mg\mathrm{cos}\theta
Sustituimos este resultado en la primera ecuación y despejamos.
mg\mathrm{sin}\theta -{\mu }_{e}mg\mathrm{cos}\theta =0
{\mu }_{e}mg\mathrm{cos}\theta =mg\mathrm{sin}\theta
\therefore {\mu }_{e}=\frac{\mathrm{sin}\theta }{\mathrm{cos}\theta }=\mathrm{tan}\theta
Comparando con las opciones, concluimos que la respuesta correcta es la c).
Reactivo 2
Se denomina ____________ al _______ sobre el cual, actúan todas las fuerzas aplicadas en un cuerpo.
- Centro de masas – punto
- Fuerza resultante – vector
- Ortocentro – lugar geométrico
Solución:
Como sabemos, los cuerpos están constituidos por partículas, entonces podríamos pensar en cualquier objeto como un conjunto de partículas rígidamente unidas (en el caso de los sólidos). A dicho conjunto se le suele denominar Sistema de Partículas del cuerpo.
Ahora, cuando una fuerza actúa sobre el SP (Sistema de Partículas), realmente se manifiesta una fuerza en la misma dirección y con igual magnitud sobre cada una de las partículas del sistema.
En lugar de trabajar con cada partícula lo que se hace es promediar espacialmente un punto dentro del SP, teniendo en cuenta la masa de cada una de ellas, sobre el que actuarán todas las fuerzas aplicadas en el cuerpo.
Dicho punto recibe el nombre de Centro de Masas abreviado CM. De esta manera, se simplifica el análisis dinámico de cuerpos rígidos, al caso de una masa puntual en el espacio. Considerando todo lo dicho y examinando las opciones, queda claro que la correcta es la a).
Se denomina Centro de Masas al Punto sobre el cual, actúan todas las fuerzas aplicadas en un cuerpo.
Reactivo 3
Dada la máquina de Atwood mostrada en la imagen, calcule la aceleración del sistema para que {m}_{1} desplace a {m}_{2} a lo largo de la rampa inclinada un ángulo \alpha . No existe fricción en el sistema. Exprese el resultado en forma algebraica.
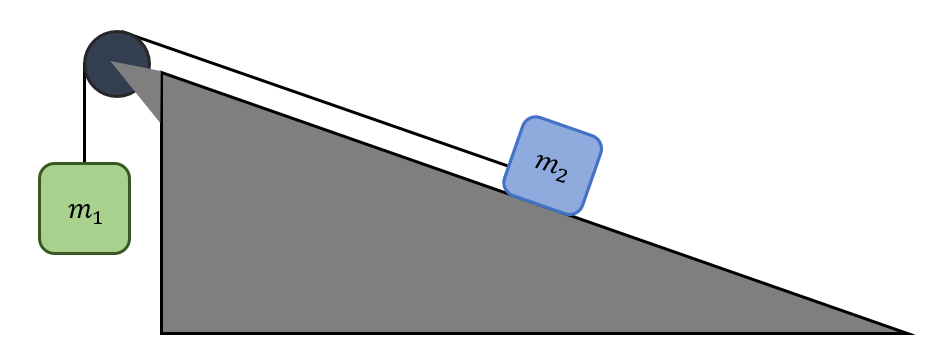
- a=\frac{{m}_{1}+{m}_{2}}{{m}_{1}}
- a=\frac{{m}_{1}g-{m}_{2}g\mathrm{sin}\alpha }{{m}_{1}+{m}_{2}}
- a=\frac{{m}_{1}-{m}_{2}}{{m}_{2}}
Solución:
Para encontrar la aceleración del sistema, debemos primero encontrar el DCL en cada bloque, teniendo en cuenta que la aceleración y la fuerza de tensión que experimentan es, en magnitud, igual.
DCL para el bloque de masa 1.
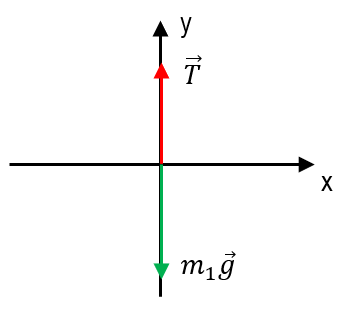
A partir del DCL de la masa 1 se obtiene la siguiente ecuación, tengamos en cuenta que la aceleración de dicha masa debe ocurrir hacia abajo, es decir, en la dirección de las -y .
\sum {F}_{1}y:T-{m}_{1}g=-{m}_{1}a
La fuerza de tensión en la cuerda seria:
T={m}_{1}g-{m}_{1}a
Ahora, hacemos el DCL para la masa 2.
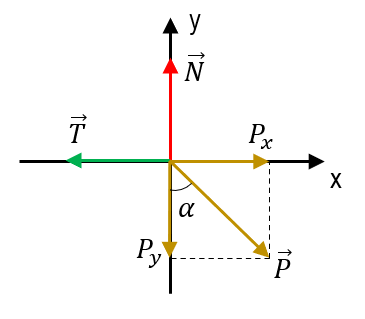
Con este diagrama de cuerpo libre de la masa 2, podemos extraer las siguientes ecuaciones. Hay que tener en cuenta que la dirección de la aceleración en este caso va en las -x .
\sum {F}_{2}x:{P}_{x}-T=-{m}_{2}a
\sum {F}_{2}y:N-{P}_{y}=0
No existe desplazamiento en y y, por tanto, la aceleración en dicho eje es cero. Despejamos la tensión de la ecuación {F}_{2}x .
T={P}_{x}+{m}_{2}a
Descomponiendo al peso, sabemos que {P}_{x}={m}_{2}g\mathrm{sin}\alpha
T={m}_{2}g\mathrm{sin}\alpha +{m}_{2}a
Igualamos ambas ecuaciones y despejamos a la aceleración.
{m}_{1}g-{m}_{1}a={m}_{2}g\mathrm{sin}\alpha +{m}_{2}a
\therefore a=\frac{{m}_{1}g-{m}_{2}g\mathrm{sin}\alpha }{{m}_{1}+{m}_{2}}
El resultado tiene lógica, ya que {m}_{1}>{m}_{2} , es decir, mientras mayor sea {m}_{1} respecto de {m}_{2} la magnitud de la aceleración será mayor, tal como se esperaría en la realidad. Comparando el resultado con las opciones, seleccionamos como correcta la b).
Reactivo 4
Un niño va sobre su bicicleta con una rapidez tangencial de 5 m/s sobre una curva perfectamente circular de radio igual a 100 metros. Calcule la aceleración centrípeta que experimenta el niño.
- 0.1 m/{s}^{2}
- 1.0 m/{s}^{2}
- 0.25 m/{s}^{2}
Solución:
Para calcular la aceleración centrípeta que experimenta el niño al desplazarse a lo largo de la curva circular, empleamos la siguiente ecuación:
{a}_{c}=\frac{{v}^{2}}{r}
Donde v es la rapidez tangencial del niño y r el radio de la curva circular. Sustituimos ambos valores en la ecuación.
{a}_{c}=\frac{{\left(5\frac{m}{s}\right)}^{2}}{100 m}=0.25 m/{s}^{2}
Comparando el resultado con las opciones, concluimos que el inciso correcto es el c).
Reactivo 5
¿Cómo se llama la fuerza que se presenta en el movimiento circular uniforme y cuál es su origen?
- Centrípeta – Aceleración centrípeta
- Centrífuga – Aceleración uniforme
- No hay ninguna fuerza
Solución:
En el movimiento circular uniforme, los cuerpos se mueven en trayectorias circulares a una velocidad angular (tasa de cambio del ángulo de barrido respecto del tiempo) constante.
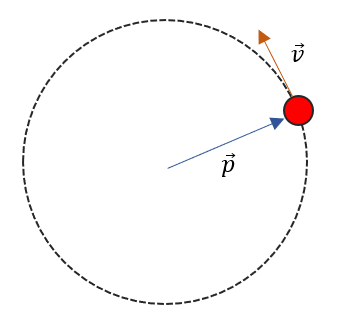
Ya que la velocidad se calcula como la derivada de la posición respecto del tiempo y, la posición depende del ángulo de barrido \theta , la expresión de la velocidad del cuerpo sobre la trayectoria circular es:
\overrightarrow{p}\left(t\right)=\mathrm{rcos}\left(\theta \left(t\right)\right)\widehat{ı}+\mathrm{rsen}\left(\theta \left(t\right)\right)\widehat{ȷ}
\overrightarrow{v}=\frac{d\overrightarrow{p}}{dt}=\overrightarrow{V}\left(t\right)=-\omega r(\mathrm{s}\mathrm{e}\mathrm{n}(\theta \left(t\right))\widehat{ı}-\mathrm{c}\mathrm{o}\mathrm{s}(\theta \left(t\right)\left)\widehat{ȷ}\right)
Al derivar respecto del tiempo a la velocidad, obtenemos la aceleración.
\overrightarrow{a}\left(t\right)=\frac{d\overrightarrow{v}}{dt}=-{\omega }^{2}r(\mathrm{c}\mathrm{o}\mathrm{s}(\theta \left(t\right))\widehat{ı}+\mathrm{s}\mathrm{e}\mathrm{n}(\theta \left(t\right))\widehat{ȷ}
Este vector va en la misma dirección, pero sentido contrario que el vector posición: radial y hacia adentro de la trayectoria curva, a esta aceleración se le conoce como aceleración centrípeta. Como consecuencia de la segunda ley de Newton, si existe una aceleración en un cuerpo también habrá una fuerza en esa dirección, así es como se origina la fuerza centrípeta.
{\overrightarrow{F}}_{c}={a}_{c}m
Concluimos entonces que la respuesta correcta se encuentra en el inciso a).
Reactivo 6
El trabajo mecánico aplicado sobre un cuerpo es máximo y positivo cuando la fuerza:
- Va en sentido contrario al desplazamiento
- Va en el mismo sentido del desplazamiento
- Es perpendicular al eje de movimiento del objeto
- 1
- 2
- 3
Solución:
De la mecánica clásica, sabemos que la ecuación para calcular el trabajo aplicado sobre un cuerpo que se desplaza una distancia \mathrm{\Delta }x es:
W=F\mathrm{\Delta }x\mathrm{cos}\theta
Donde \theta es el ángulo entre la fuerza y un vector que va en el sentido del desplazamiento. De esta forma, el trabajo será máximo y positivo si el ángulo entre dichos vectores es cero, es decir, son vectores paralelos.
W=F\mathrm{\Delta }x\mathrm{cos}0°=F\mathrm{\Delta }x
Concluimos entonces que la respuesta correcta es la b).
Reactivo 7
Un objeto puntual de masa m=2 kg se mueve en una trayectoria circular con una rapidez angular de 1 rad/s . Si la curva posee radio igual a 1 metro, calcule la energía cinética rotacional que posee el objeto puntual.
- -1 J
- 0 J
- 1 J
Solución:
Sabemos que la energía cinética lineal se calcula como:
{E}_{c}=\frac{1}{2}m{v}^{2}
Si en dicha ecuación sustituimos a la velocidad tangencial v por su equivalente en velocidad rotacional v=\omega r , obtenemos que:
{E}_{c}=\frac{1}{2}m{\left(\omega r\right)}^{2}=\frac{1}{2}m{\omega }^{2}{r}^{2}
Sustituimos los valores dados por el enunciado en la ecuación.
{E}_{c}=\frac{1}{2}\left(2Kg\right){\left(1 rad/s\right)}^{2}{\left(1m\right)}^{2}=1 J
Comparando con las opciones, seleccionamos como correcta la c).
Reactivo 8
Dado el sistema de partículas de la figura, calcule:
- Su inercia rotacional
- La energía rotacional del sistema si gira a 1 rad/s
Considere que todas las partículas tienen la misma masa m=1 \mathrm{k}\mathrm{g} y que el eje de rotación se coloca en el origen.
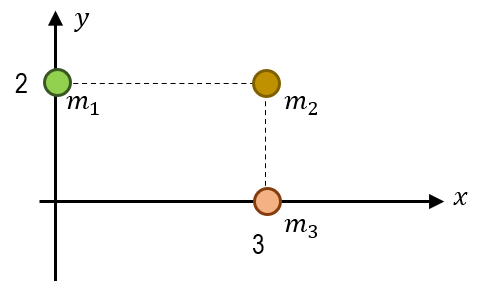
- {I}_{SP}=2 \mathrm{k}\mathrm{g}\bullet \mathrm{m};{E}_{c}=100 \mathrm{J}
- {I}_{SP}=26 \mathrm{k}\mathrm{g}\bullet \mathrm{m};{E}_{c}=13 \mathrm{J}
- {I}_{SP}=13 \mathrm{k}\mathrm{g}\bullet \mathrm{m};{E}_{c}=26 \mathrm{J}
Solución:
La inercia rotacional de un sistema de partículas discreto (cantidad finita de partículas), se obtiene a partir de la siguiente ecuación:
I=\sum {m}_{i}{r}_{i}^{2}
Donde {m}_{i} es la masa de cada partícula y {r}_{i} es la distancia desde el eje de rotación hasta la partícula en cuestión. Sabemos que la masa de todas las partículas es igual, pero nos falta calcular los radios de cada una.
Radio de {m}_{1} .
{r}_{1}=2
Radio de {m}_{2} .
{r}_{2}=\sqrt{{3}^{2}+{2}^{2}}=\sqrt{13}
Radio de {m}_{3} .
{r}_{3}=3
Sustituimos en la ecuación de inercia rotacional:
{I}_{SP}={m}_{1}{r}_{1}^{2}+{m}_{2}{r}_{2}^{2}+{m}_{3}{r}_{3}^{2}=\left(1 \mathrm{k}\mathrm{g}\right)\left(4 \mathrm{m}+13 \mathrm{m}+9 \mathrm{m}\right)
{I}_{SP}=26 \mathrm{k}\mathrm{g}\bullet \mathrm{m}
Ahora, la energía cinética rotacional de un SP se calcula mediante la siguiente ecuación:
{E}_{c}=\frac{1}{2}I{\omega }^{2}
Sustituimos los valores:
{E}_{c}=\frac{1}{2}\left(26 \mathrm{k}\mathrm{g}\bullet \mathrm{m}\right){\left(1\frac{\mathrm{r}\mathrm{a}\mathrm{d}}{\mathrm{s}}\right)}^{2}=13 J
Comparando con las opciones, seleccionamos como correcta la b).
Reactivo 9
Teniendo en cuenta el principio de conservación del momento angular para un sistema aislado como el que se muestra en la figura.
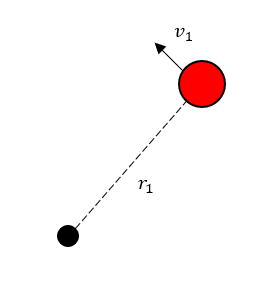
¿Qué le sucederá a la velocidad angular si se reduce el radio de rotación respecto al eje?
- Aumenta la velocidad angular
- Disminuya la velocidad angular
- Se mantiene igual
Solución:
Si tenemos en cuenta el principio de conservación del momento angular, en un sistema aislado cualquiera el momento lineal total {L}_{1} en un instante inicial será igual al momento lineal total {L}_{2} en un instante posterior.
{L}_{1}={L}_{2}
Ya que nuestro sistema solo está compuesto por la bola en rotación, la igualdad quedaría como:
m{r}_{1}^{2}{\omega }_{1}=m{r}_{2}^{2}{\omega }_{2}
Despejando la velocidad angular en el instante 2.
{\omega }_{2}={\left(\frac{{r}_{1}}{{r}_{2}}\right)}^{2}{\omega }_{1}
Por simple aritmética, si {r}_{2}<{r}_{1} el cociente de ambas cantidades será mayor que la unidad y, por ende, la velocidad angular {\omega }_{2} será mayor que {\omega }_{1} . Concluimos entonces que la respuesta correcta es la opción a).
Reactivo 10
Se tiene un sistema de partículas rotando en sentido de las manecillas del reloj. ¿Cuál será la dirección del momento angular del sistema?
- Perpendicular y saliendo del plano de rotación
- Paralelo a la velocidad tangencial
- Perpendicular y entrando al plano de rotación
Solución:
Para responder esta pregunta, debemos recordar la definición vectorial del momento angular:
\overrightarrow{L}=m\overrightarrow{r}\times \overrightarrow{v}
Es el producto vectorial entre el radio vector y la velocidad tangencial del sistema de partículas.
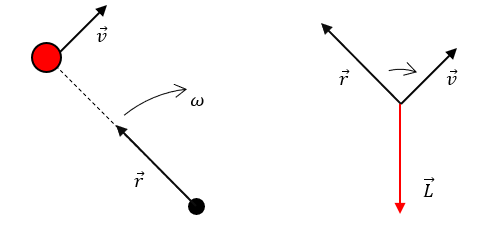
En base a la regla de la mano derecha, el vector momento angular apunta perpendicular y hacia adentro del plano inclinado. Concluimos entonces que la respuesta correcta es la c).
Reactivo 11
Un motociclista se desplaza a una velocidad de 90 kilómetros por hora y con dicha velocidad entra a una curva perfectamente circular con radio igual a 2.5 metros. Si el sistema motocicleta-humano tiene una masa total de 150 kilogramos, ¿cuál es la fuerza centrípeta que experimenta?
- 25500 N
- 15000 N
- 37500 N
Solución:
La segunda ley de Newton nos dice que la fuerza es igual al producto de la masa de un cuerpo por su aceleración.
F=m\bullet a
Para simplificar la solución (ya que no es relevante) trabajaremos a la fuerza y la aceleración como módulos y no como vectores. Debes tener muy presente esto último al resolver cualquier ejercicio de física.
Examinando la situación planteada en el enunciado, queda claro que se trata de un MCU (movimiento circular uniforme) por tanto, la aceleración que debemos utilizar en la fórmula es la centrípeta y cuya ecuación (en módulo) es la siguiente:
{a}_{c}=\frac{{v}^{2}}{r}
Para sustituir la rapidez (módulo de la velocidad) y el radio, debemos comprobar las unidades. Es necesario transformar la velocidad a metros por segundo, el radio permanece igual.
v=90\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}\bullet \frac{1 \mathrm{h}}{3600 \mathrm{s}}\bullet \frac{1000 \mathrm{m}}{1 \mathrm{k}\mathrm{m}}=25\frac{\mathrm{m}}{\mathrm{s}}
m=150 \mathrm{k}\mathrm{g}
Ahora sí, sustituimos:
F=\left(150 \mathrm{k}\mathrm{g}\right)\frac{{\left(25\frac{\mathrm{m}}{\mathrm{s}}\right)}^{2}}{2.5} =37,500 \mathrm{N}
La fuerza centrípeta es de 37500 Newtons. Comparando con las opciones, la respuesta correcta es el inciso c).
Reactivo 12
Una bailarina de ballet se encuentra interpretando su rutina en las clasificatorias para las olimpiadas. Alguien en el público nota que, al girar, si mantiene su pierna extendida lo hace más lento que cuando recoge su cuerpo. ¿Qué fenómeno físico está visualizando el espectador?
- Conservación del momento lineal
- Conservación de la masa
- Conservación del momento angular
Solución:
Para explicar este fenómeno, debemos recordar el concepto de momento angular y la condición para su conservación. El momento angular, es una magnitud vectorial análoga al momento lineal que indica la cantidad de giro posee un sistema físico.
Ahora, salvando el concepto de sistema físico, sabemos que mientras que cualquier sistema no interactúa con su exterior, este permanece invariante. Por tal motivo, si un sistema en rotación no experimenta un torque externo su cantidad de rotación permanece invariante.
Esto es lo que conocemos como conservación del momento angular.
{L}_{i}={L}_{f}
Llevando esto a la bailarina, (teniendo en cuenta que la interacción con el viento y el hielo es despreciable) debido a que no interacciona con el exterior, al recoger su cuerpo reduce el radio de rotación y, según la conservación del momento, esto se traduce en un incremento de la velocidad.
Concluimos el reactivo indicando como respuesta correcta la opción c).
Reactivo 13
¿Cuál es el peso del semáforo, en newtons, si se encuentra en equilibrio?
Considere: coseno de 30°=0.866 y seno de 30°=0.5.
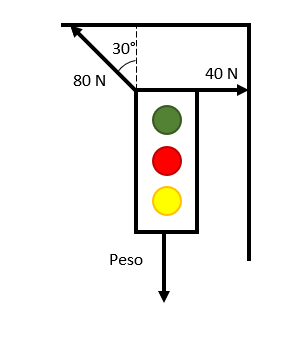
- 29.28
- 40.00
- 69.28
Solución:
Para calcular el peso del semáforo, debemos descomponer las fuerzas que están actuando sobre él, en el eje x y en el eje y , e igualar cada ecuación resultante a cero, tal como lo indica la primera condición estática de Newton. Procedemos a descomponer la fuerza con ángulo de 30°.
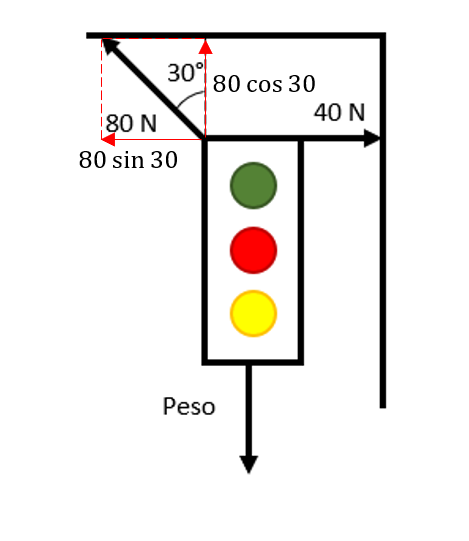
En este caso no es necesario hacer el balance de fuerzas en el eje x porque en él no se encuentra ninguna incógnita, solo haremos el balance sobre el eje y .
\sum {F}_{y}:80 \cos\left(30\right) -W=0
Despejamos al peso W .
W=80 \cos \left(30\right) =69.28 N
El peso del semáforo es igual a 69.28 Newtons.
Comparando con las opciones, la respuesta correcta es la opción C.
Reactivo 14
Ana corre en una pista circular cuyo perímetro es de 3 km. Si corre 2 vueltas en 2 horas, ¿Cuál es su velocidad angular?
- 0.00 rad/s
- 3 km/h
- 2\pi rad/h
Solución:
Cuando un movimiento tiene lugar en una trayectoria curva, se define la velocidad angular \omega como el ángulo que barre el radio vector por unidad de tiempo. En el sistema internacional, la velocidad angular se mide en radianes por segundo \left[\frac{rad}{s}\right] , pero en algunos casos también se mide en radianes por hora \left[\frac{rad}{h}\right] .
\omega =\frac{\Delta \theta }{\Delta t}
En este caso, sabemos que la niña recorre dos vueltas, expresadas en forma de ángulo equivale a 4\pi rad , por otro lado, el intervalo de tiempo en el que recorre ambas vueltas es \Delta t=2 h . Sustituimos ambos valores en la fórmula de velocidad angular y calculamos.
\omega =\frac{4\pi rad}{2 h}=2\pi rad/h
La velocidad angular de la niña es de 2\pi rad/h .
La respuesta correcta es la opción C.
Reactivo 15
Un bloque con masa de 3 kg está en reposo sobre un plano inclinado. Si el coeficiente de fricción estático entre el bloque y el plano inclinado es {\mu }_{s} , ¿Cuáles ecuaciones satisfacen las condiciones de equilibrio que muestra la imagen?
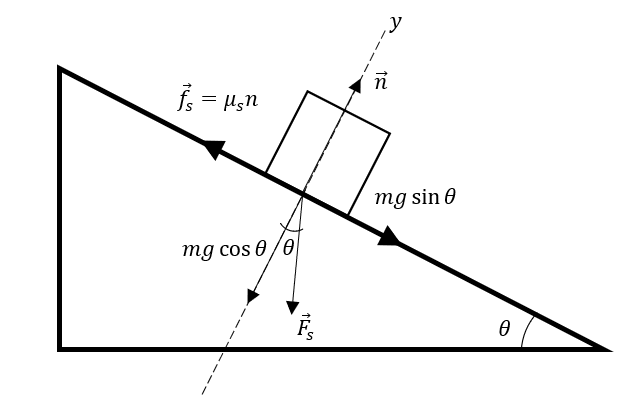
- \sum {F}_{x}=\mathrm{mgsen}\theta -{\mu }_{s}n=0 \sum {F}_{y}=n-mgcos\theta =0
- \Sigma {F}_{x}=mgcos\theta -{\mu }_{s}n=0 \Sigma {F}_{y}=n-mgsen\theta =0
- \sum {F}_{x}=n-mgcos\theta =0 \sum {F}_{y}=mgsen\theta -{\mu }_{s}n=0
Solución:
Para encontrar el sistema de ecuaciones que describe la situación estática de la figura, debemos descomponer las fuerzas en los ejes x y y , aplicar sumatoria en ambas e igualar a cero. Comencemos por el eje y .
En el eje y actúa la componente vertical de {F}_{s} es decir, mgcos\theta en dirección negativa y la fuerza normal n que va en dirección vertical positiva. La ecuación en el eje y queda:
\sum {F}_{y}:n-mgcoscos \theta =0
Ahora, vamos con la componente x , la misma ha sido definida sobre la superficie del plano inclinado para facilitar los cálculos. En sentido positivo de las x tenemos a la componente horizontal del peso mg sin\theta y en sentido opuesto la fuerza de roce estática {\overrightarrow{f}}_{s}={\mu }_{s}n . La expresión quedaría como:
{\sum }_{}^{}{F}_{x}:mgsin\theta -{\mu }_{s}n=0
Finalmente, el sistema de ecuaciones que describen la estática del sistema.
{\sum }_{}^{}{F}_{x}:mgsin\theta -{\mu }_{s}n=0
{\sum }_{}^{}{F}_{y}:n-mgcoscos \theta =0
Comparando con las opciones, la respuesta correcta es la A.
Reactivo 16
La aceleración que se presenta en un móvil se debe a:
- Que la suma de fuerzas internas es cero
- La aplicación de una fuerza interna
- La aplicación de una fuerza externa
Solución:
La segunda ley de Newton establece una relación entre la fuerza externa neta que se aplica a un cuerpo y la aceleración que este adquiere. Así, se puede afirmar que la aceleración de cualquier partícula tiene en todo momento la misma dirección y el mismo sentido de la fuerza neta que actúa sobre ella.
Hablando en términos generales, se establece que la sumatoria de las fuerzas externas aplicadas sobre un cuerpo es proporcionalmente igual a la aceleración que experimenta.
{F}_{neta}=ma
El caso general
{\sum }_{}^{}F=ma
En base a nuestro análisis teórico, podemos concluir seleccionando como respuesta correcta la opción C.
Reactivo 17
Si un objeto con masa de 110 kg se lanza verticalmente hacia arriba a una velocidad inicial de 30 km/h, ¿Cuántos metros de altura alcanza?
Considere g=9.81m/{s}^{2} .
- 3.53
- 34.7
- 45.87
Solución:
Cuando un cuerpo es lanzado verticalmente hacia arriba, considerando el caso ideal donde se supone que no hay resistencia al viento, no es necesario emplear las ecuaciones de Newton, sólo las clásicas fórmulas de cinemática para el lanzamiento vertical hacia arriba, estas ecuaciones son:
{V}_{f}={V}_{0}-gt
{V}_{f}^{2}={V}_{0}^{2}-2gh
y={V}_{0}t-\frac{1}{2}g{t}^{2}
En un lanzamiento hacia arriba, la máxima altura se alcanza cuando la velocidad final {V}_{f} es igual a cero, por tanto, podremos despejar la altura con la segunda ecuación.
0={V}_{0}^{2}-2g{h}_{max}\to {h}_{max}=\frac{{V}_{o}^{2}}{2g}
Antes de sustituir, es necesario transformar la velocidad inicial a metros por segundo.
{V}_{o}=30\frac{km}{h}*\frac{1000 m}{1 km}*\frac{1 h}{3600 s}=8.33 m/s
Sustituimos.
{h}_{max}=\frac{{\left(8.33\frac{m}{s}\right)}^{2}}{2\left(9.81m/{s}^{2}\right)}=3.53 m
La altura que alcanza el cuerpo es de 3.53 metros.
La respuesta correcta es la opción A.
Reactivo 18
Dos cuerpos se encuentran en movimiento lineal y en direcciones opuestas, de tal forma que en determinado momento chocan. Luego del choque, ambos cuerpos quedan unidos y desplazandoce a la misma velocidad final v_{f} , de tal forma que la energía cinética final es cero. ¿Cómo se clasifica el choque entre los cuerpos?
- Choque perfectamente inelástico
- Choque elástico
- Choque inelástico
Solución:
Los choques se clasifican en tres grupos: elásticos, inelásticos y perfectamente inelásticos. El estudio de los choques parte de estudiarlos como un solo sistema, por tanto, siempre se conserva la cantidad de movimiento en él pero, no en todos los casos se conserva la energía del sistema.
Cuando un choque es elástico, los cuerpos hacen contacto y salen repelidos sin cambios en sus estructuras.
Por otro lado, en los choques inelásticos y perfectamente inelásticos, los cuerpos se deforman y, para ello, es necesario efectuar trabajo en la estructura del objeto, ocasionando que parte de la energía se disipe en forma de calor.
Con todo esto en cuenta y analizando el enunciado, podemos concluir que la respuesta correcta es la a).
Reactivo 19
La inercia rotacional es una cantidad análoga a…
- La energía cinética
- El trabajo mecánico
- La masa inercial
Solución:
La inercia rotacional o momento de inercia, es una cantidad que cuantifica la resistencia de los cuerpos a los cambios en su movimiento rotacional. Esto último resulta familiar a la definición de masa en base a la segunda ley de Newton.
En este contexto, la masa suele denominarse masa inercial, de cara a la resistencia de los objetos a cambios en su movimiento traslacional.
\sum{\vec{F}}=m\vec{a}
Esta expresión es análoga a la definición de torca en dinámica rotacional, donde el momento de torsión o torca es proporcional a la aceleración angular que experimenta un cuerpo y dicha constante de proporcionalidad es la inercia rotacional.
\sum{\vec{\tau}}=I\vec{\alpha}
La respuesta correcta es el inciso c).
Reactivo 20
Juan necesita extraer una tuerca demasiado ajustada que sostiene una de las llantas de su carro. Está utilizando una llave inglesa de 30 cm de largo y él ejerce una fuerza de 20 N con cierto ángulo \theta . Si el torque necesario para extraer la tuerca es de 3 Nm, ¿cuál es el ángulo mínimo que debe adoptar Juan al aplicar la fuerza?
- 30°
- 25°
- 45°
Solución:
Para resolver este problema, debemos recordar la ecuación para calcular el torque aplicado sobre un cuerpo:
\tau =rF\mathrm{sin}\theta
Donde r es el radio o distancia entre el eje de rotación y el punto donde se aplica la fuerza, F es la magnitud de la fuerza y \theta es el ángulo entre la fuerza y el objeto. Despejamos de la fórmula al seno de theta.
\mathrm{sin}\theta =\frac{\tau }{rF}
Sustituimos.
\mathrm{sin}\theta =\frac{3 \mathrm{N}\mathrm{m}}{\left(0.3 \mathrm{m}\right)\left(20 \mathrm{N}\right)}=\frac{1}{2}
Ahora, debemos encontrar el ángulo que, evaluado en el seno, da como resultado \frac{1}{2} . Recordando los temas de trigonometría, dicho ángulo es 30°.
\theta =30°
Finalmente, el mínimo ángulo no mayor a 90° que debe tener Juan respecto a la herramienta es de 30°. Concluimos que la respuesta correcta está en el inciso a).
Reactivo 21
Un estudiante se encuentra dando vueltas en una silla de escritorio con los pies encogidos de forma vertical. En esta posición, el estudiante tiene una inercia rotacional de 0.4 {\mathrm{k}\mathrm{g}\bullet \mathrm{m}}^{2} . Cuando estira las piernas de forma horizontal, la inercia rotacional aumenta a 0.6 {\mathrm{k}\mathrm{g}\bullet \mathrm{m}}^{2} . Si la rapidez angular antes de estirar las piernas era de 0.2 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s} , ¿cuál es la rapidez angular al estirar las piernas?
- 0.16 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}
- 0.4 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}
- 0.012 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}
Solución:
Para este problema, recordemos el principio de conservación del momento angular:
{L}_{i}={L}_{f}
En este caso aplica, debido a que el muchacho no interactúa con torques externos. Se comporta como un sistema aislado. Escribimos la ecuación completa.
\frac{1}{2}{I}_{1}{\omega }_{1}^{2}=\frac{1}{2}{I}_{2}{\omega }_{2}^{2}
Despejamos la rapidez angular final y la sustituimos.
{\omega }_{2}=\sqrt{\frac{{I}_{1}}{{I}_{2}}{\omega }_{1}^{2}}=0.16 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}
Este resultado tiene sentido, porque la forma de compensar el aumento en la inercia rotacional ocurre disminuyendo la rapidez angular. Comparando con las opciones, la respuesta correcta es el inciso a).
Reactivo 22
Una pelota se dirige hacia la izquierda con una rapidez de 12 \mathrm{m}/\mathrm{s} . Al hacer contacto con la pierna de un jugador, la pelota choca y sale despedida con un ángulo de 45° hacia la derecha en horizontal, hacia abajo en vertical y con una magnitud de 20 \mathrm{m}/\mathrm{s} . Calcula el vector impulso considerando una masa de 0.25 \mathrm{k}\mathrm{g} para el balón.
- \left(0.5 \widehat{i}-0.5 \widehat{j}\right) \mathrm{k}\mathrm{g}\bullet \mathrm{m}/\mathrm{s}
- \left(0.535 \widehat{i}-3.535 \widehat{j}\right) \mathrm{k}\mathrm{g}\bullet \mathrm{m}/\mathrm{s}
- \left(12 \widehat{i}-20 \widehat{j}\right) \mathrm{k}\mathrm{g}\bullet \mathrm{m}/\mathrm{s}
Solución:
Antes de pasar a calcular propiamente el impulso que solicita el enunciado, debemos establecer las componentes de los vectores de velocidad antes y después de la colisión. Comencemos con {v}_{1} que tiene dirección horizontal y hacia la izquierda.
{v}_{1}=-12 \widehat{i} \mathrm{m}/\mathrm{s}
Para el segundo vector, debemos calcular las componentes descomponiéndose en la horizontal y la vertical. Los módulos de cada componente son:
{v}_{2x}=20\mathrm{cos}45°=14.14 \mathrm{m}/\mathrm{s}
{v}_{2y}=20\mathrm{sin}45°=14.14 \mathrm{m}/\mathrm{s}
Escribimos la solución en forma canónica. La componente horizontal queda positiva y la vertical negativa porque apunta hacia abajo.
{v}_{2}=\left(14.14 \widehat{i}-14.14 \widehat{j}\right) \mathrm{m}/\mathrm{s}
Con los vectores de velocidad establecidos, procedemos a calcular el impulso componente a componente:
{J}_{x}=m\left({v}_{2x}-{v}_{1x}\right)
{J}_{y}=m\left({v}_{2y}-{v}_{1y}\right)
Sustituimos:
{J}_{x}=\left(0.25 \mathrm{k}\mathrm{g}\right)\left(14.14 \mathrm{m}/\mathrm{s}-12 \mathrm{m}/\mathrm{s}\mathrm{ }\right)=0.535 \mathrm{k}\mathrm{g}\bullet \mathrm{m}/\mathrm{s}
{J}_{y}=\left(0.25 \mathrm{k}\mathrm{g}\right)\left(-14.14 \mathrm{m}/\mathrm{s}-0\mathrm{ }\right)=-3.535 \mathrm{k}\mathrm{g}\bullet \mathrm{m}/\mathrm{s}
Finalmente, el vector impulso de la pelota es:
J=\left(0.535 \widehat{i}-3.535 \widehat{j}\right) \mathrm{k}\mathrm{g}\bullet \mathrm{m}/\mathrm{s}
La respuesta correcta se encuentra en el incisob).
Reactivo 23
Si la fuerza electrostática entre 2 cargas situadas a una distancia r es 10 N, ¿Cuál debe ser la distancia entre las cargas para que la fuerza de atracción sea 40 N?
- \frac{r}{4}
- \frac{r}{2}
- 2r
Solución:
La ley de Coulomb para la electroestática, permite calcular la magnitud y dirección de la fuerza de atracción o repulsión entre dos partículas cargadas eléctricamente. En este caso, solo nos interesa la magnitud de dicha fuerza, la cual se calcula de la siguiente manera:
{F}_{e}=\frac{{k}_{e}\left|{q}_{1}{q}_{2}\right|}{{r}^{2}}
Donde r es la distancia entre las cargas y \left|{q}_{1}{q}_{2}\right| es el valor absoluto del producto entre las cargas, esto para asegurar un resultado positivo. Ahora, sabemos que a una distancia r , la fuerza de atracción entre las cargas del enunciado es 10 N. Sustituyamos para ver qué nos queda:
10=\frac{{k}_{e}\left|{q}_{1}{q}_{2}\right|}{{r}^{2}}
Luego, la fuerza aumenta a 40 N y desconocemos la distancia {r}_{2} que provoca dicha fuerza de interacción.
40=\frac{{k}_{e}\left|{q}_{1}{q}_{2}\right|}{{r}_{2}^{2}}
Si observamos ambas expresiones, el producto {k}_{e}\left|{q}_{1}{q}_{2}\right| se repite en ambas, por tanto, despejémoslo para luego igualar.
10=\frac{{k}_{e}\left|{q}_{1}{q}_{2}\right|}{{r}^{2}}\to 10{r}^{2}={k}_{e}\left|{q}_{1}{q}_{2}\right|
40=\frac{{k}_{e}\left|{q}_{1}{q}_{2}\right|}{{r}_{2}^{2}}\to 40{r}_{2}^{2}={k}_{e}\left|{q}_{1}{q}_{2}\right|
Igualamos.
10{r}^{2}=40{r}_{2}^{2}
Despejamos a {r}_{2} .
{r}_{2}^{2}=\frac{{r}^{2}}{4}
{r}_{2}=\frac{r}{2}
La distancia entre las cargas debe ser \frac{r}{2} para que la fuerza de atracción se incremente a 40 N.
Comparando con las opciones, la respuesta correcta es la B.
Reactivo 24
El voltaje aplicado al circuito de la figura es de 12 V y las resistencias R1,R2 y R3 son de 5, 3 y 8 \Omega respectivamente. ¿Cuál es la resistencia equivalente del circuito, en ohm?
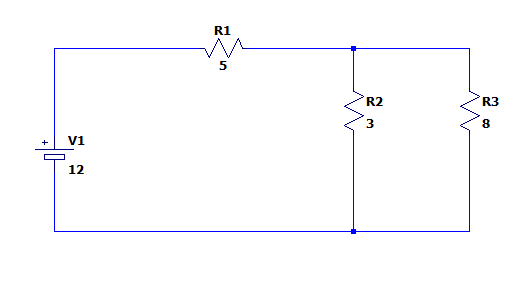
- 5.45
- 7.18
- 16
Solución:
Cuando se solicita calcular la resistencia equivalente en un circuito eléctrico, normalmente se hace respecto de la fuente de alimentación que se encuentra en él, en este caso la fuente {v}_{1}=12 V .
Existen muchos métodos para el cálculo de resistencia equivalente, pero debido a lo sencillo del circuito, solo debemos desconectar la fuente y entre sus terminales, hallar una única resistencia aplicando serie y paralelo.
Desconectamos la fuente de alimentación.
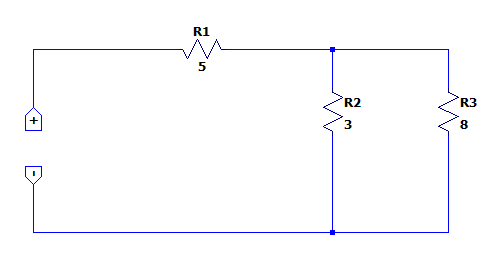
Aplicamos paralelo entre las resistencias {R}_{2} y {R}_{3} .
{R}_{2}\left|\right|{R}_{3}=\frac{{R}_{2}{R}_{3}}{{R}_{2}+{R}_{3}}
Sustituimos.
{R}_{2}\left|\right|{R}_{3}=\frac{\left(3\right)\left(8\right)}{3+8}=2.18 \Omega
El circuito queda de la siguiente forma.
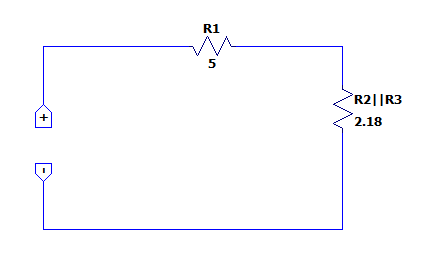
Por último, queda hacer la serie entre {R}_{1} y {R}_{2}\left|\right|{R}_{3} .
{R}_{1}+{R}_{2}\left|\right|{R}_{3}=5+2.18=7.18 \Omega

La resistencia equivalente del circuito en terminales de la fuente es 7.18 \Omega .
La respuesta correcta es la opción B.
Reactivo 25
De acuerdo con el circuito, ¿cuál es la corriente total, en amperios, que entrega la fuente de voltaje?
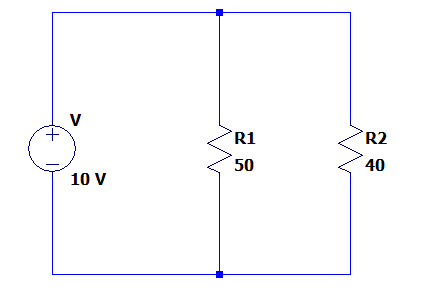
- 0.05 A
- 0.45 A
- 0.8 A
Solución:
Para calcular la corriente que entrega la fuente a las dos resistencias, debemos aplicar la Ley de Corrientes de Kirchhoff en el nodo de conexión de la fuente con las resistencias.
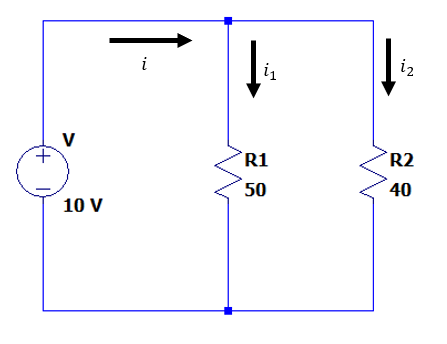
La corriente de la fuente es igual a la suma de las corrientes a través de las resistencias.
i={i}_{1}+{i}_{2}
Por ley de Ohm, sabemos que la corriente en un resistor es igual al cociente del voltaje en terminales y la resistencia, en este caso, ambas resistencias tienen el mismo voltaje de la fuente porque están conectadas a ella en paralelo.
{i}_{1}=\frac{V}{{R}_{1}}
{i}_{2}=\frac{V}{{R}_{2}}
Sustituimos.
i=V\left(\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}}\right)
i=10\left(\frac{1}{50}+\frac{1}{40}\right)=0.45 A
La corriente que otorga la fuente a los resistores es de 0.45 amperios.
Escogemos como correcta la opción B.
Reactivo 26
En general, los metales son buenos conductores de la electricidad por…
- Sus propiedades físicas.
- Ser resistentes al calor.
- Tener pocos electrones en la última órbita de sus átomos.
Solución:
En los conductores eléctricos, las cargas pueden moverse con total libertad a través del material, mientras que en los aisladores no pueden hacerlo. El experimento de Hall, deja en manifiesto que, en conductores metálicos, las cargas que conforman la corriente eléctrica son solo los electrones.
Cuando un conjunto de átomos se unen para formar un sólido metálico, los electrones de las capas exteriores se separan de los átomos, quedando libres para moverse en todo el volumen del material.
En estado no excitado, los electrones se mueven de forma aleatoria dentro del material, pero cuando se establece un campo eléctrico, por ejemplo, al conectar una batería, los electrones se alinean con el campo desplazándose todos en una misma dirección.
Con todo lo anterior, concluimos que la respuesta correcta es la opción C: por tener pocos electrones en la última órbita de sus átomos.
Reactivo 27
Si la corriente en el circuito que se muestra en la figura es de 2 A, ¿Cuál es el valor del voltaje total?
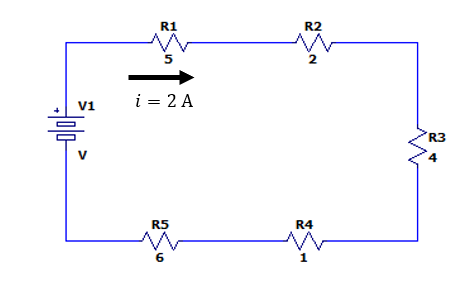
- 0.11 V
- 9.00 V
- 36.00 V
Solución:
Debido a que todas las resistencias se encuentran conectadas en serie, por ellas circula la misma corriente de 2 amperios. Además, si aplicamos la Ley de voltajes de Kirchhoff, la tensión de la pila es igual a la suma de las caídas en las resistencias.
V={V}_{1}+{V}_{2}+{V}_{3}+{V}_{4}+{V}_{5}
Por ley de Ohm, sustituimos V=iR .
V={i}_{1}{R}_{1}+{i}_{2}{R}_{2}+{i}_{3}{R}_{3}+{i}_{4}{R}_{4}+{i}_{5}{R}_{5}
Ya que la corriente i es la misma para todas, la extraemos como factor común.
V=i\left({R}_{1}+{R}_{2}+{R}_{3}+{R}_{4}+{R}_{5}\right)
Sustituimos los valores de corriente y resistencias.
V=\left(2 A\right)\left(5+2+4+1+6\right)
V=36 V
Para que circule una corriente de 2 amperios por el circuito serie, la fuente debe ser de 36 voltios.
Comparando con las opciones, la respuesta correcta es la C.
Reactivo 28
¿Qué resistencia tiene una parrilla eléctrica de 120 V que consume una corriente de 22 A?
- 5.45
- 18.33
- 120
Solución:
Para calcular la resistencia eléctrica de la parrilla, debemos emplear la ley de Ohm.
R=\frac{V}{I}
El cociente entre el voltaje y la corriente que circula por la parrilla, es igual a la resistencia eléctrica de la misma. Sustituimos los valores.
R=\frac{120 V}{22 A}=5.45 \Omega
La parrilla ofrece una resistencia de 5.45 \Omega al paso de la corriente.
Escogemos como correcta la opción A.
Reactivo 29
Una onda electromagnética que se propaga en el vacío con una velocidad c=3\times10^{8} \mathrm{m/s} , posee una frecuencia de 5\times10^{14} \mathrm{Hz} . Si el espectro visible se encuentra entre los 750 y 400 nanómetros de longitud de onda, ¿es visible la onda electromagnética anterior?
- Se encuentra en el espectro visible
- No se encuentra en el espectro visible
- Es una onda muy energética
Solución:
Sin importar la naturaleza de la onda, todas pueden describirse a través de parámetros escalares tales como: frecuencia, período, longitud de onda y velocidad de propagación. Además, estas tres cantidades se encuentran relacionadas a partir de una simple ecuación.
v=\lambda f
Donde \lambda es la longitud de onda, v la velocidad y f la frecuencia.
Para responder a la pregunta del enunciado, debemos verificar que la longitud de la onda electromagnética se encuentre dentro del rango de 750 a 400 nanómetros. Procedemos a calcular la longitud de onda con los datos proporcionados.
\lambda=\frac{v}{f}=\frac{3 \times 10^{8} \mathrm{~m} / \mathrm{s}}{5 \times 10^{14} \mathrm{~Hz}}=600 \mathrm{~nm}
La onda electromagnética tiene una longitud de onda igual a 600 nanómetros, se encuentra dentro del espectro visible.
La respuesta correcta es la a).
Reactivo 30
Seleccione los dispositivos eléctricos que almacenan energía.
- Capacitor.
- Resistencia.
- Interruptor.
- Bobina.
- 1, 2
- 1, 4
- 2, 3
Solución:
Entre los dispositivos eléctricos, el condensador y el inductor o bobina son capaces de almacenar energía eléctrica. Por una parte, el capacitor almacena la energía en forma de campo eléctrico, mientras que el inductor o bobina lo hace en forma de campo magnético.
Teniendo en cuenta lo anterior, los incisos correctos son el 1 y el 4. Concluimos indicando que la respuesta al reactivo es la opción B 1 y 4.
Reactivo extra: Campo magnético producido por un alambre
¿Cuál es la inducción magnética, en teslas, a 10 cm de un alambre conductor recto y largo que conduce una corriente de 5 A?
Considere {\mu }_{0}=1.3\times {10}^{-6}Tm/A .
- 10\times {10}^{-7}
- 1.0\times {10}^{-5}
- 6.3\times {10}^{-5}
Solución:
Para un conductor rectilíneo de longitud considerable o infinita (como este caso), la intensidad del campo magnético generado en un punto situado a una distancia r del alambre, está dada por la siguiente ecuación:
B=\frac{{\mu }_{o}}{2\pi }\bullet \frac{I}{r}
Donde:
- I es la intensidad de la corriente.
- r la distancia respecto del alambre.
- {\mu }_{o} la permeabilidad magnética del vacío.
Para nuestro caso, la intensidad de la corriente I=5 A , la distancia entre el punto y el alambre r=10 cm o r=0.1 m y la permeabilidad {\mu }_{0}=1.3\times {10}^{-6}Tm/A . Sustituimos la expresión y calculamos la intensidad del campo magnético.
B=\frac{1.3\times {10}^{-6}Tm/A}{2\pi }\bullet \frac{5 A}{0.1 m}=1.03\times {10}^{-5} T
Comparando con los resultados de los incisos, queda claro que es una aproximación a la opción B. Escogemos como correcta a la B.
Reactivo extra: Propiedades de la luz
¿Cuál propiedad de la luz se presenta cuando al meter un lápiz dentro de un vaso con agua este aparece como si estuviera quebrado?
- Reflexión.
- Dispersión.
- Refracción.
Solución:
La luz viaja a velocidades diferentes en medios diferentes. Esta es una de las razones por las cuales, la luz se desvía de su dirección original cuando pasa de un medio a otro.
Experimentalmente, se puede comprobar que la luz cambia de dirección cuando va de un medio a otro, un ejemplo clásico es la situación del lápiz descrita en el enunciado. Al fenómeno del cambio de dirección de la luz al atravesar dos medios se le conoce como refracción.
Teniendo en cuenta el análisis anterior, indicamos como correcta la opción C.

