Llegamos a la tercera y última parte del simulacro resuelto de Cálculo diferencial e integral del módulo 4 para la prueba de ingreso EXANI. Vamos a la solución de los reactivos del 21 al 30.

Aquí puedes ver algunos ítems destacables referentes al Exani II:
- Desarrollo: Ceneval
- Examen de admisión: Exani II
- Reactivos: 168
- Tipo: Opción múltiple
- Duración: 4 horas y media
- Modalidades: Presencial, en línea y desde casa.
De nuevo te sugerimos: resuélvelos por tu cuenta antes de ver la respuesta. Obtener una buena calificación depende del tiempo y la energía que inviertas durante tu preparación.
Estructura del Exani II
El Exani II de Ceneval consta de dos partes, la primera evalúa conocimientos generales como pensamiento matemático y comprensión lectora, mientras que la segunda se enfoca en áreas de conocimiento específicas.
Los módulos de conocimiento específico que encontrarás en el examen son 2, y varían en función de la carrera a la que apliques.
En la siguiente tabla te mostramos la estructura general del Exani II:
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Temario de Cálculo diferencial e integral
Cálculo diferencial e integral es uno de los 16 módulos específicos que conforman el Exani II, siendo uno de los más desafiantes. Para conocer los temas que puedes encontrar en el examen, consulta el temario completo:
- Subárea: Cálculo diferencial
- Propiedades de los límites
- Límites de funciones polinomiales y con variables independientes
- Derivadas por definición, de funciones trigonométricas, de funciones exponenciales y logarítmicas y de
- funciones polinomiales
- Recta tangente de funciones algebraicas
- Aplicaciones físicas de la derivada (velocidad instantánea, distancia, rapidez de cambio y de optimización)
- Subárea: Cálculo integral
- Partición de funciones
- Manipulación algebraica y aritmética
- Propiedades de la integral
- Métodos de integración
- Problemas de área, volumen y movimiento con integrales definidas
Ejercicios de Cálculo diferencial e integral
Al finalizar este simulacro, habrás repasado todos los temas de cálculo que van para la segunda parte del EXANI II. No te detengas en este punto, identifica tus fallas, posibles mejoras y ¡toma un descanso! también forma parte del proceso de aprendizaje.
Reactivo 21
Relacione el cambio de variable con el método de resolución de integrales al que corresponde.
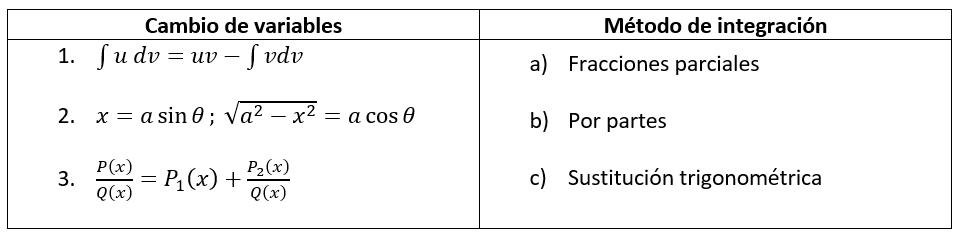
- 1b, 2a, 3c
- 1c, 2b, 3a
- 1b, 2c, 3a
Solución:
Vamos a definir cada uno de los métodos de integración de la columna derecha para luego relacionarlo con el cambio de variables de la columna izquierda.
Fracciones parciales.
Se aplica cuando tenemos funciones racionales, en las que tanto el numerador como el denominador son polinomios. La técnica consiste en descomponer al cociente \frac{P\left(x\right)}{Q\left(x\right)} en una suma de funciones racionales que resulte más sencilla de integrar. De ahí, que el nombre del método sea fracciones parciales o fracciones simples.
Para este caso: 3a.
Por partes.
Este método realmente está basado en la fórmula de la derivada de un producto de dos funciones. La técnica toma la fórmula del diferencial de un producto:
d\left(uv\right)=vdu+udv
Y se aplica integración de ambos lados.
\int d\left(uv\right)=\int vdu+\int udv
Como sabemos el diferencial se cancela con la integral quedando:
uv=\int vdu+\int udv
Por convención, decimos que la integral \int udv es más compleja y que se trata precisamente de la que estamos intentando resolver, mientras que \int vdu es más simple de resolver. Despejando nos queda:
\int udv=uv-\int vdu
Con este “artificio” hemos simplificado la integral. Concluimos para este caso que:
1b.
Sustitución trigonométrica.
Este cambio de variables nos permite convertir una integral algebraica con raíces complicadas, en otra de tipo trigonométrica más sencilla. El método se sustenta en que el integrando debe ser de la forma:
\sqrt{{a}^{2}-{x}^{2}}; \sqrt{{x}^{2}-{a}^{2}}; \sqrt{{a}^{2}+{x}^{2}}
Luego, se traslada esto en un triángulo rectángulo, como si se tratase del teorema de Pitágoras y se establecen las siguientes igualdades:
\begin{array}{c}x=a\mathrm{sin}\theta ; \sqrt{{a}^{2}-{x}^{2}}=a\mathrm{cos}\theta \\ x=a\mathrm{sec}\theta ; \sqrt{{x}^{2}-{a}^{2}}=a\mathrm{tan}\theta \\ x=a\mathrm{tan}\theta ; \sqrt{{a}^{2}-{x}^{2}}=a\mathrm{sec}\theta \end{array}
Concluimos entonces que: 2c.
Uniendo todas las respuestas, nos queda: 1b, 2c, 3a. Comparando con las opciones, seleccionamos como correcta la c).
Reactivo 22
Calcule la siguiente integral aplicando el método más conveniente para ello.
\int \frac{z+1}{{z}^{2}-4z+8}dz
- \frac{1}{2}\mathrm{ln}\left|{z}^{2}-4z+8\right|+C
- \mathrm{ln}\left|{z}^{2}-4z+8\right|+\frac{3}{2}{\mathrm{tan}}^{-1}\left(\frac{z-2}{2}\right)+C
- \frac{1}{2}\mathrm{ln}\left|{z}^{2}-4z+8\right|+\frac{3}{2}{\mathrm{tan}}^{-1}\left(\frac{z-2}{2}\right)+C
Solución:
Lo primero que podríamos intentar para resolver esta integral, es factorizar el numerador e intentar simplificar el binomio del numerador, pero si lo intentamos, nos encontraremos con el problema de que {z}^{2}-4z+8 tiene raíces complejas conjugadas.
Solo nos queda intentar aplicar un cambio de variables al denominador, para ello haremos que el numerador se parezca a la derivada del denominador. Multiplicamos y dividimos por 2.
\frac{1}{2}\int \frac{2\left(z+1\right)}{{z}^{2}-4z+8}dz=\frac{1}{2}\int \frac{2z+2}{{z}^{2}-4z+8}dz
Sumamos y restamos 6 para construir al -4.
\frac{1}{2}\int \frac{2z+2+6-6}{{z}^{2}-4z+8}dz=\frac{1}{2}\int \frac{2z-4+6}{{z}^{2}-4z+8}dz
Ahora, 2z-4 es la derivada de {z}^{2}-4z+8 , pero no está incluido el +6, es necesario separar la integral.
\frac{1}{2}\int \frac{2z-4+6}{{z}^{2}-4z+8}dz=\frac{1}{2}\int \frac{2z-4}{{z}^{2}-4z+8}dz+\frac{1}{2}\int \frac{6}{{z}^{2}-4z+8}dz
Vamos a partir la solución en dos integrales:
{I}_{1}=\frac{1}{2}\int \frac{2z-4}{{z}^{2}-4z+8}dz
{I}_{2}=\frac{1}{2}\int \frac{6}{{z}^{2}-4z+8}dz
Resolviendo la primera integral.
{I}_{1}=\frac{1}{2}\int \frac{2z-4}{{z}^{2}-4z+8}dz
Aplicamos el cambio de variables.
u={z}^{2}-4z+8\to du=\left(2z-4\right)dz
Sustituimos.
{I}_{1}=\frac{1}{2}\int \frac{1}{u}du
Aplicamos la integral del inverso de la variable.
{I}_{1}=\frac{1}{2}\int \frac{1}{u}du=\frac{1}{2}\mathrm{ln}\left|u\right|+{c}_{1}
Devolvemos el CV.
\frac{1}{2}\mathrm{ln}\left|u\right|+{c}_{1}\equiv \frac{1}{2}\mathrm{ln}\left|{z}^{2}-4z+8\right|+{c}_{1}
Resolviendo la segunda integral.
{I}_{2}=\frac{1}{2}\int \frac{6}{{z}^{2}-4z+8}dz
Para esta integral, vamos a transformar a {z}^{2}-4z+8 en {\left(z+a\right)}^{2}+b .
{z}^{2}+2az+{a}^{2}+b={z}^{2}-4z+8
2a=-4\to a=-2
{a}^{2}+b=8\to b=4
{I}_{2}=\frac{1}{2}\int \frac{6}{{\left(z-2\right)}^{2}+4}dz=\frac{1}{2}\int \frac{6}{{\left(z-2\right)}^{2}+{2}^{2}}dz
Aplicamos el cambio:
v=z-2\to dv=dz
Sustituimos.
{I}_{2}=3\int \frac{1}{{v}^{2}+{2}^{2}}dv
Esto corresponde a una integral inmediata.
{I}_{2}=3\int \frac{1}{{v}^{2}+{2}^{2}}dv=\frac{3}{2}{\mathrm{tan}}^{-1}\frac{v}{2}+{c}_{2}
Devolvemos el cambio de variable.
\frac{3}{2}{\mathrm{tan}}^{-1}\frac{v}{2}+{c}_{2}\equiv \frac{3}{2}{\mathrm{tan}}^{-1}\left(\frac{z-2}{2}\right)+{c}_{2}
Unimos ambas soluciones:
I={I}_{1}+{I}_{2}=\frac{1}{2}\mathrm{ln}\left|{z}^{2}-4z+8\right|+\frac{3}{2}{\mathrm{tan}}^{-1}\left(\frac{z-2}{2}\right)+C
Finalmente:
\int \frac{z+1}{{z}^{2}-4z+8}dz=\frac{1}{2}\mathrm{ln}\left|{z}^{2}-4z+8\right|+\frac{3}{2}{\mathrm{tan}}^{-1}\left(\frac{z-2}{2}\right)+C
Comparando con las opciones, la respuesta correcta es la c).
Reactivo 23
Resuelva la siguiente integral aplicando el método por partes.
\int {x}^{2}{\mathrm{tan}}^{-1}xdx
- \frac{{x}^{3}}{3}{\mathrm{tan}}^{-1}x-\frac{1}{6}{x}^{2}+\frac{1}{6}\mathrm{ln}\left|1+{x}^{2}\right|+C
- \frac{{x}^{3}}{3}{\mathrm{tan}}^{-1}x-\frac{1}{6}{x}^{2}+\mathrm{ln}\left|1+{x}^{2}\right|+C
- \frac{{x}^{3}}{3}{\mathrm{tan}}^{-1}x+\frac{1}{6}{x}^{2}+\frac{1}{6}\mathrm{ln}\left|1+{x}^{2}\right|+C
Solución:
Para resolver una integral con el método por partes, es necesario escoger cuál de las funciones será u y cual será v . Se suele emplear la regla de ILATE, pero no es lo más recomendable. Falla, más aún cuando los integrandos son complejos. El mejor truco para seleccionar la función correcta es la práctica.
En este caso, vamos a derivar a {\mathrm{tan}}^{-1}x porque luego de esta operación, se convierte en algebraica.
u={\mathrm{tan}}^{-1}x\to du=\frac{1}{1+{x}^{2}}dx
dv={x}^{2}dx\to v=\frac{{x}^{3}}{3}
Sustituimos en la ecuación del método.
\int u dv=uv-\int vdu
\int {x}^{2}{\mathrm{tan}}^{-1}xdx=\frac{{x}^{3}}{3}{\mathrm{tan}}^{-1}x-\frac{1}{3}\int \frac{{x}^{3}}{1+{x}^{2}}dx
Ahora, vamos a aplicar división de polinomios sobre el integrando \frac{{x}^{3}}{1+{x}^{2}} , lo que resulta en:
\frac{{x}^{3}}{1+{x}^{2}}=x-\frac{x}{1+{x}^{2}}
Sustituimos y separamos la integral.
=\frac{{x}^{3}}{3}{\mathrm{tan}}^{-1}x-\frac{1}{3}\int \left(x-\frac{x}{1+{x}^{2}}\right)dx=\frac{{x}^{3}}{3}{\mathrm{tan}}^{-1}x-\frac{1}{3}\int xdx+\frac{1}{3}\int \frac{x}{1+{x}^{2}}dx
En la integral del último término se puede multiplicar y dividir por 2.
\frac{{x}^{3}}{3}{\mathrm{tan}}^{-1}x-\frac{1}{3}\int xdx+\frac{1}{3}\int \frac{x}{1+{x}^{2}}dx=\frac{{x}^{3}}{3}{\mathrm{tan}}^{-1}x-\frac{1}{3}\int xdx+\frac{1}{6}\int \frac{2x}{1+{x}^{2}}dx
Aplicando introducción al símbolo del diferencial ya que:
d\left(1+{x}^{2}\right)=2xdx
=\frac{{x}^{3}}{3}{\mathrm{tan}}^{-1}x-\frac{1}{3}\int xdx+\frac{1}{6}\int \frac{d\left(1+{x}^{2}\right)}{1+{x}^{2}}
Integramos.
=\frac{{x}^{3}}{3}{\mathrm{tan}}^{-1}x-\frac{1}{6}{x}^{2}+\frac{1}{6}\mathrm{ln}\left|1+{x}^{2}\right|+C
Finalmente, concluimos seleccionando como respuesta correcta la opción a).
Reactivo 24
Calcular el valor de la integral aplicando sustitución trigonométrica.
\int \frac{1}{{\left(4-{x}^{2}\right)}^{3/2} }dx
- \frac{1}{4}\frac{1}{\sqrt{4-{x}^{2}}}+C
- \frac{1}{4}\frac{x}{\sqrt{4-{x}^{2}}}+C
- \frac{1}{4}\sqrt{4-{x}^{2}}+C
Solución:
Para identificar cuál de los tres posibles cambios debemos aplicar en la integral, expresamos al segundo término del radicando como una potencia.
\int \frac{1}{{\left({2}^{2}-{x}^{2}\right)}^{3/2} }dx
Para este caso, aplicamos el siguiente cambio:
x=a\mathrm{sin}\theta ; \sqrt{{a}^{2}-{x}^{2}}=a\mathrm{cos}\theta
Donde a=2 .
\int \frac{1}{{\left({2}^{2}-{x}^{2}\right)}^{3/2} }dx=\int \frac{1}{{\left(\sqrt{{2}^{2}-{x}^{2}}\right)}^{3} }dx
Sustituimos.
dx=2\mathrm{cos}\theta d\theta
\int \frac{2\mathrm{cos}\theta }{{\left(2\mathrm{cos}\theta \right)}^{3} }d\theta =\int \frac{2\mathrm{cos}\theta }{8{\mathrm{cos}}^{3}\theta }d\theta =\frac{1}{4}\int \frac{1}{{\mathrm{cos}}^{2}\theta }d\theta =\frac{1}{4}\int {\mathrm{sec}}^{2}\theta d\theta
Aplicamos la integral directa de la secante al cuadrado.
\frac{1}{4}\int {\mathrm{sec}}^{2}\theta d\theta =\frac{1}{4}\mathrm{tan}\theta +C
Devolvemos el cambio trigonométrico.
\mathrm{tan}\theta =\frac{x}{\sqrt{{2}^{2}-{x}^{2}}}
\frac{1}{4}\mathrm{tan}\theta +C=\frac{1}{4}\frac{x}{\sqrt{4-{x}^{2}}}+C
Finalmente:
\int \frac{1}{{\left(4-{x}^{2}\right)}^{3/2} }dx=\frac{1}{4}\frac{x}{\sqrt{4-{x}^{2}}}+C
Concluimos entonces que la respuesta correcta es la opción b).
Reactivo 25
Resuelva la siguiente integral aplicando el método de fracciones parciales.
\int \frac{dx}{{x}^{2}+3x-10}
- -\frac{1}{7}\mathrm{ln}\left|x+5\right|+\frac{1}{7}\mathrm{ln}\left|x-2\right|+C
- -\frac{1}{7}\mathrm{ln}\left|x+5\right|+C
- \mathrm{ln}\left|x+5\right|+\frac{1}{7}\mathrm{ln}\left|x-2\right|+C
Solución:
Para aplicar fracciones parciales, debemos separar a la fracción propia en dos o más fracciones sencillas cuya integración sea también sencilla. Comencemos por factorizar el polinomio del denominador.
\frac{1}{{x}^{2}+3x-10}=\frac{1}{\left(x+5\right)\left(x-2\right)}
Este corresponde al primer caso de fracciones parciales.
\frac{1}{\left(x+5\right)\left(x-2\right)}=\frac{A}{x+5}+\frac{B}{x-2}
Pasamos al segundo miembro los factores del denominador.
1=A\left(x-2\right)+B\left(x+5\right)
1=Ax-2A+Bx+5B\to 1=\left(A+B\right)x-2A+5B
Igualamos los coeficientes.
A+B=0
-2A+5B=1
Resolviendo el sistema de ecuaciones obtenemos que:
A=-\frac{1}{7};B=\frac{1}{7}
\frac{1}{\left(x+5\right)\left(x-2\right)}=\frac{-1}{7\left(x+5\right)}+\frac{1}{7\left(x-2\right)}
Sustituimos en la integral.
\int \frac{dx}{{x}^{2}+3x-10}=\int \left(\frac{-1}{7\left(x+5\right)}+\frac{1}{7\left(x-2\right)}\right)dx=-\frac{1}{7}\int \frac{dx}{x+5}+\frac{1}{7}\int \frac{dx}{x-2}
Integramos aplicando la fórmula correspondiente.
-\frac{1}{7}\int \frac{dx}{x+5}+\frac{1}{7}\int \frac{dx}{x-2}=-\frac{1}{7}\mathrm{ln}\left|x+5\right|+\frac{1}{7}\mathrm{ln}\left|x-2\right|+C
Finalmente:
\int \frac{dx}{{x}^{2}+3x-10}=-\frac{1}{7}\mathrm{ln}\left|x+5\right|+\frac{1}{7}\mathrm{ln}\left|x-2\right|+C
Concluimos indicando que la respuesta correcta es la opción a).
Reactivo 26
Dada la función f\left(x\right)=\frac{1}{x-1} , ¿es posible calcular su integral definida en el intervalo \left[0, 1\right] ?
- Si, porque la función tiene antiderivada
- No, porque f\left(x\right) no es continua en dicho intervalo
- Es posible siempre que se haga con el método por partes
Solución:
A partir del segundo teorema fundamental del cálculo, es posible encontrar el valor numérico de una integral. Geométricamente, esto corresponde a obtener el área debajo de la curva en el intervalo de integración dado.
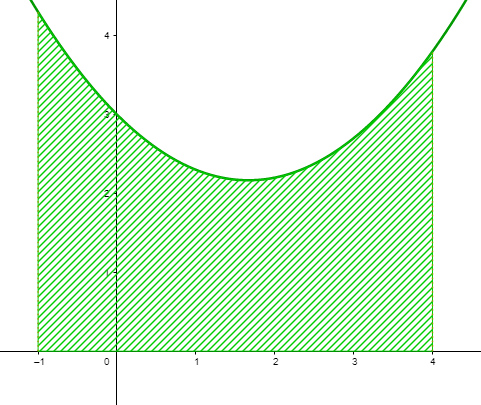
Para poder aplicar dicho teorema, deben cumplirse dos condiciones:
- Que la función f sea continua en el intervalo
- Que la función sea integrable, es decir, que posea primitiva
Examinando estas condiciones en la función dada, vemos que la misma presenta una discontinuidad de salto infinito en x=1 y, tal como dice el teorema, la función debe ser continua en todo el intervalo incluidos los extremos, pero f\left(x\right) no cumple. Concluimos entonces que:
No es posible integrar en el intervalo dado porque la función no es continua en él.
Comparando con las opciones, indicamos como correcta la b).
Reactivo 27
Calcule el área bajo la curva en el intervalo desde -2 hasta 4.
i={\int }_{-2}^{4}\left({x}^{3}-6x+2\right)dx
- i=36
- i=-36
- i=63
Solución:
Para aplicar el segundo teorema fundamental del cálculo, debemos comprobar que la función sea continua en el intervalo de integración. Debido a que f\left(x\right)={x}^{3}-6x+2 es continua para todo R , lo es también en el intervalo dado.
Integramos indefinidamente.
i={\int }_{-2}^{4}\left({x}^{3}-6x+2\right)dx={\int }_{-2}^{4}{x}^{3}dx-6{\int }_{-2}^{4}xdx+2{\int }_{-2}^{4}dx
Aplicamos las fórmulas de integración directa correspondientes.
{\int }_{-2}^{4}{x}^{3}dx-6{\int }_{-2}^{4}xdx+2{\int }_{-2}^{4}dx=\left(\frac{{x}^{4}}{4}-3{x}^{2}+2x\right]\begin{array}{c}4\\ -2\end{array}
Evaluamos.
\left(\frac{{x}^{4}}{4}-3{x}^{2}+2x\right]\begin{array}{c}4\\ -2\end{array}=\frac{{4}^{4}}{4}-3{\left(4\right)}^{2}+2\left(4\right)-\left[\frac{{\left(-2\right)}^{4}}{4}-3{\left(-2\right)}^{2}+2\left(-2\right)\right]=36
Finalmente:
i={\int }_{-2}^{4}\left({x}^{3}-6x+2\right)dx=36
Concluimos el ejercicio escogiendo la opción a) como respuesta correcta.
Reactivo 28
Calcule el área entre las curvas f\left(x\right)=3-{x}^{2} y g\left(x\right)=x+1 . Tenga en cuenta que la gráfica de las curvas es la siguiente:
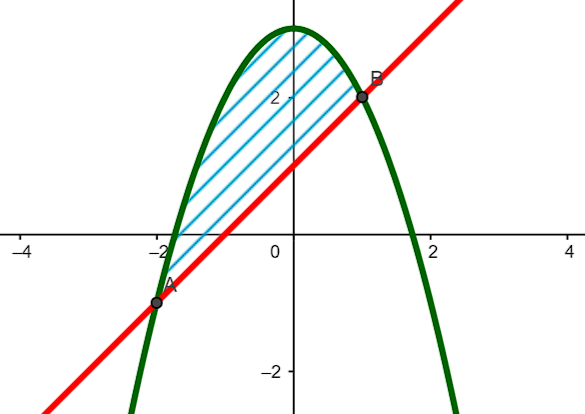
- A\left(f,g\right)=\frac{9}{2}
- A\left(f,g\right)=\frac{2}{9}
- A\left(f,g\right)=-\frac{9}{2}
Solución:
Para calcular el área entre dos curvas, debemos identificar el caso en el que nos encontramos: rectángulos verticales o rectángulos horizontales. Esto corresponde a la orientación de los rectángulos infinitesimales, para identificarlo, trazamos un rectángulo horizontal y otro vertical, que toquen ambas curvas. Seleccionamos la orientación del rectángulo que no atraviese intersecciones entre las curvas.
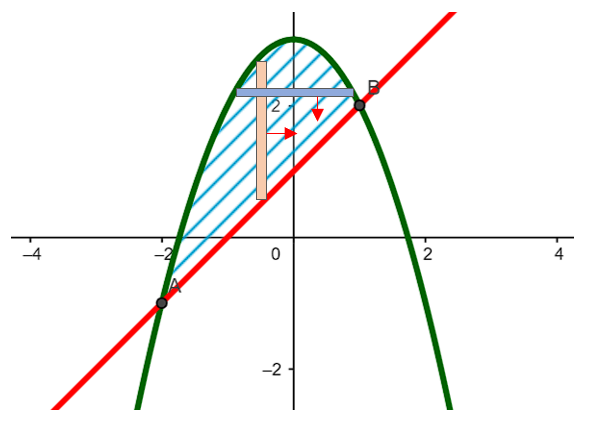
Si hacemos el ejercicio de desplazar los rectángulos en el área sombreada, nos daremos cuenta que el rectángulo vertical nunca atraviesa intersecciones entre las curvas, por otro lado, el horizontal sí que lo hace, pasa por la intersección B antes de terminar su recorrido.
Rectángulos verticales.
A={\int }_{a}^{b}\left[función superior-función inferior\right]dx
En nuestro caso, la función superior es f\left(x\right)=3-{x}^{2} y la inferior es g\left(x\right)=x+1 . Sustituimos en la integral.
A={\int }_{a}^{b}\left[3-{x}^{2}-\left(x+1\right)\right]dx={\int }_{a}^{b}\left[-{x}^{2}-x+2\right]dx
Ahora, solo nos falta encontrar los límites de integración. Para ello, encontramos las coordenadas en x de los puntos de intersección entre las curvas. Igualamos las funciones.
3-{x}^{2}=x+1\to {x}^{2}+x-2=0
\left(x+2\right)\left(x-1\right)=0
Las coordenadas en x son:
{x}_{a}=-2;{x}_{b}=1
La integral quedaría:
{\int }_{-2}^{1}\left[-{x}^{2}-x+2\right]dx=\left(-\frac{{x}^{3}}{3}-\frac{{x}^{2}}{2}+2x\right]\begin{array}{c}1\\ -2\end{array}
A=-\frac{1}{3}-\frac{1}{2}+2-\left(\frac{8}{3}-2-4\right)=\frac{9}{2}
El área entre las curvas es:
A\left(f,g\right)=\frac{9}{2}
Concluimos seleccionando como correcta la opción a).
Reactivo 29
Calcule la longitud de la curva semicúbica y={x}^{\frac{3}{2}} , en el intervalo de x\in \left[0, 5\right] . Tenga en cuenta que la ecuación para calcular la longitud de una curva respecto de x es:
L={\int }_{a}^{b}\sqrt{1+{\left[{f}^{\text{'}}\left(x\right)\right]}^{2}}dx
- \frac{35}{27}
- \frac{335}{27}
- \frac{1}{27}
Solución:
Primero, debemos calcular la derivada de la curva respecto de x , la cual quedaría de la siguiente manera.
{y}^{\text{'}}=\frac{3}{2}{x}^{\frac{1}{2}}
Sustituimos en la ecuación integral, junto a los límites de integración.
L={\int }_{0}^{5}\sqrt{1+{\left[\frac{3}{2}{x}^{\frac{1}{2}}\right]}^{2}}dx={\int }_{0}^{5}\sqrt{1+\frac{9}{4}x}dx=\frac{1}{2}{\int }_{0}^{5}\sqrt{4+9x}dx
Aplicamos un sencillo cambio de variables.
u=4+9x\to du=9dx\to dx=\frac{1}{9}du
L=\frac{1}{18}{\int }_{0}^{5}\sqrt{u}du=\left(\frac{1}{18}\frac{{\left(u\right)}^{\frac{3}{2}}}{\frac{3}{2}}\right]\begin{array}{c}\begin{array}{c}5\\ \end{array}\\ \\ 0\end{array}=\frac{1}{27}\left({\left(4+9x\right)}^{\frac{3}{2}}\right]\begin{array}{c}5\\ \\ 0\end{array}
L=\frac{335}{27}
Concluimos escogiendo como respuesta correcta la opción b).
Reactivo 30
Las superficies de revolución son aquellas que se forman al hacer girar una curva plana alrededor de un eje de rotación fijo. Dicho eje puede ser uno de los ejes coordenados o alguna otra recta de interés. La siguiente figura muestra un ejemplo de superficie de revolución.
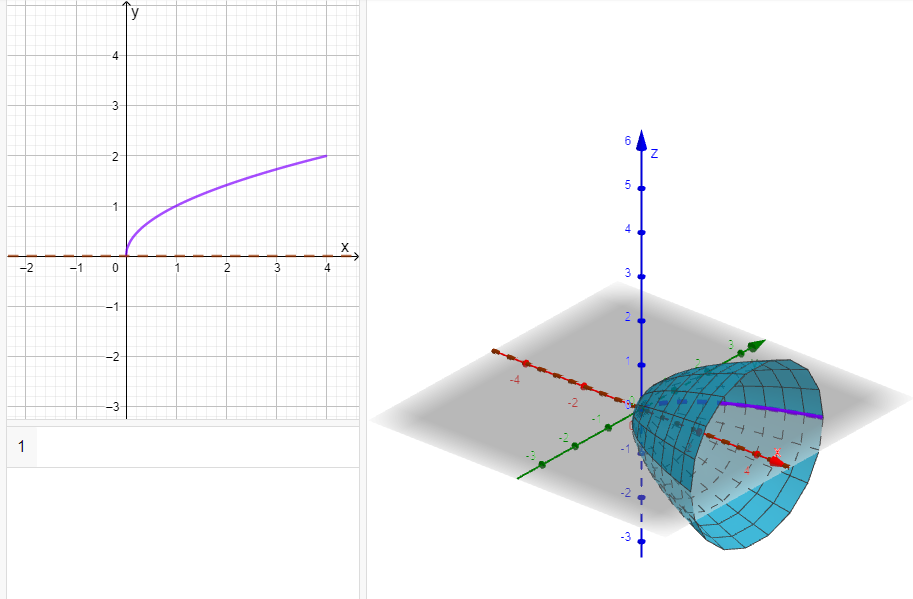
La curva plana es y=\sqrt{x} , la cual se ha hecho girar alrededor del eje x para dar con la superficie de la derecha. A partir del cálculo integral, es posible calcular el área de la superficie generada, en el caso de utilizar al eje x para la rotación, la ecuación que se deduce es:
A=2\pi {\int }_{a}^{b}f\left(x\right)\sqrt{1+{\left({f}^{\text{'}}\left(x\right)\right)}^{2}}dx
Calcula el área que se genera al hacer revolucionar la curva y=\sqrt{x} alrededor del eje x en el tramo x\in \left[0, 4\right] .
- 36 {u}^{2}
- 36.1 {u}^{2}
- 36.177 {u}^{2}
Solución:
Tal como se muestra en la ecuación integral, necesitamos calcular la derivada de la función, por tanto:
{f}^{\text{'}}\left(x\right)=\frac{1}{2\sqrt{x}}
Sustituimos en la integral los límites y las funciones.
A=2\pi {\int }_{0}^{4}\left(\sqrt{x}\right)\sqrt{1+{\left(\frac{1}{2\sqrt{x}}\right)}^{2}}dx=2\pi {\int }_{0}^{4}\left(\sqrt{x}\right)\sqrt{1+{\left(\frac{1}{2\sqrt{x}}\right)}^{2}}dx
Simplificamos.
2\pi {\int }_{0}^{4}\left(\sqrt{x}\right)\sqrt{1+\frac{1}{4x}}dx=2\pi {\int }_{0}^{4}\left(\sqrt{x}\right)\sqrt{\frac{4x+1}{4x}}dx=2\pi {\int }_{0}^{4}\sqrt{x} \frac{\sqrt{4x+1}}{2\sqrt{x}}dx
=\pi {\int }_{0}^{4} \sqrt{4x+1}dx
Aplicamos un sencillo cambio de variables.
u=4x+1\to du=4dx\to dx=\frac{1}{4}du
=\frac{\pi }{4}{\int }_{0}^{4} \sqrt{u}du=\frac{\pi }{6}\left({u}^{\frac{3}{2}}\right]\begin{array}{c}4\\ \\ 0\end{array}=\frac{\pi }{6}\left({\left(4x+1\right)}^{\frac{3}{2}}\right]\begin{array}{c}4\\ \\ 0\end{array}
Evaluamos.
A=\frac{\pi }{6}\left[{\left(16+1\right)}^{\frac{3}{2}}-{\left(0+1\right)}^{\frac{3}{2}}\right]=\frac{\pi }{6}\left[{\left(17\right)}^{\frac{3}{2}}-1\right]=\frac{\pi }{6}\left(17\sqrt{17}-1\right)
Finalmente:
A=\frac{\pi }{6}\left(17\sqrt{17}-1\right)\approx 36.177 {u}^{2}
Concluimos que la respuesta correcta es la opción c).


