Guía Exani II Cálculo Diferencial e Integral: 30 Ejercicios P.2

¡Hola de nuevo aspirante! En este tutorial vamos a resolver los reactivos del 11 al 21, correspondientes a la segunda parte de los ejercicios de Cálculo diferencial e integral del simulacro del módulo 4 para el examen de ingreso EXANI.

Desarróllalos por tu cuenta antes de mirar las soluciones y mide el tiempo que tardas con cada parte. Es importante que tengas rapidez antes de la fecha del examen.

Ejercicios de Cálculo diferencial e integral

Seguimos con la segunda parte del simulacro de Cálculo para EXANI. Una vez hayas resuelto los problemas, analiza el procedimiento, identifica las posibles fallas y puntos de mejora para acortar el tiempo.

Reactivo 11

Determine la pendiente de la recta tangente en el punto $x=-1$, para la siguiente función:

$f\left(x\right)={\mathrm{sin}}^{-1}\left(x+1\right)$

1. $m=-1$
2. $m=1$
3. $m=\infty$

Solución:

Como sabemos de la teoría de cálculo diferencial, la interpretación geométrica de la derivada de una función $f\left(x\right)$, es que corresponde a la pendiente de la recta tangente a dicha función en un determinado punto $x={x}_{0}$.

Es decir, con la derivada evaluada en $x={x}_{0}$ y las coordenadas del punto $P\left({x}_{0},{y}_{0}\right)$ obtenemos la recta que es tangente a la función en dicho punto. Comencemos entonces por derivar a $f\left(x\right)$.

${f}^{\text{'}}\left(x\right)={\left[{\mathrm{sin}}^{-1}\left(x+1\right)\right]}^{\text{'}}$

${f}^{\text{'}}\left(x\right)=\frac{{\left(x+1\right)}^{\text{'}}}{\sqrt{1-{\left(x+1\right)}^{2}}}$

Simplificamos.

${f}^{\text{'}}\left(x\right)=\frac{{\left(x+1\right)}^{\text{'}}}{\sqrt{1-{\left(x+1\right)}^{2}}}=\frac{1}{\sqrt{1-\left({x}^{2}+2x+1\right)}}$

$=\frac{1}{\sqrt{1-\left({x}^{2}+2x+1\right)}}=\frac{1}{\sqrt{-{x}^{2}-2x}}$

$\therefore {f}^{\text{'}}\left(x\right)=\frac{1}{\sqrt{-{x}^{2}-2x}}$

Ahora, determinamos el valor de la pendiente en $x=-1$ como:

$m={f}^{\text{'}}\left(-1\right)=\frac{1}{\sqrt{-{\left(-1\right)}^{2}-2\left(-1\right)}}=\frac{1}{\sqrt{-1+2}}=\frac{1}{\sqrt{1}}$

$\therefore m=1$

Si construimos rápidamente la ecuación de la recta tenemos:

$m=1, {x}_{0}=-1$

${y}_{0}={\mathrm{sin}}^{-1}\left(-1+1\right)=0$

${P}_{0}\left(-1, 0\right)$

$y-{y}_{0}=m\left(x-{x}_{0}\right)$

$y-0=1\left(x+1\right)$

$y=x+1$

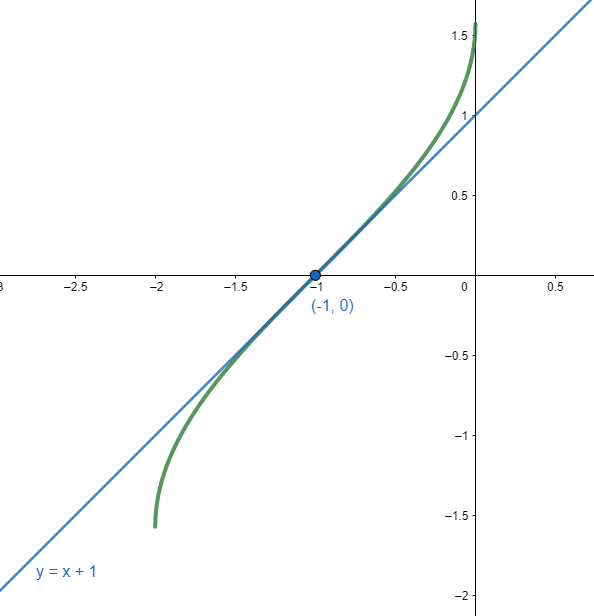
Concluimos entonces que la respuesta correcta es la opción b).

Reactivo 12

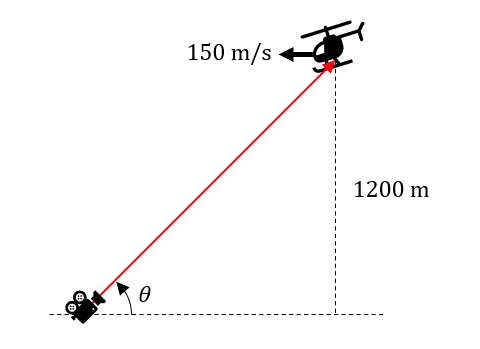
Un helicóptero vuela al oeste (sentido horizontal negativo) con una velocidad de $150 \mathrm{m}/\mathrm{s}$ a una altura de 1200 metros y una cámara de alta velocidad rastrea su movimiento desde tierra. La luz se debe mantener sobre el vehículo en todo momento, ¿cuál es la función que describe el cambio del ángulo de inclinación de la cámara respecto del tiempo, en función de la coordenada horizontal del helicóptero?

1. $\frac{d\theta }{dt}=\frac{18000}{{x}^{2}+{1200}^{2}}$
2. $\frac{d\theta }{dt}=\frac{180000}{{x}^{2}+{1200}^{2}}$
3. $\frac{d\theta }{dt}=\frac{180000}{{x}^{2}}$

Solución:

Para responder este problema correctamente, primero debemos encontrar una ecuación que relacione al ángulo $\theta$, con la coordenada en $x$ del helicóptero. Aplicando trigonometría básica encontramos que:

$\mathrm{tan}\theta =\frac{1200}{x}$

Ahora, la variación del ángulo respecto del tiempo la encontramos derivando la ecuación anterior.

 
$\frac{d}{dt}\left(\mathrm{tan}\theta \right)=\frac{d}{dt}\left(\frac{1200}{x}\right)$

Derivamos aplicando la regla de la cadena y de forma implícita.

${\mathrm{sec}}^{2}\theta \frac{d\theta }{dt}=-\frac{1200}{{x}^{2}}\frac{dx}{dt}$

De la cinemática clásica, sabemos que la velocidad de un cuerpo es igual a la variación de su posición respecto del tiempo, debido a que la velocidad es constante, sustituimos $\frac{dx}{dt}$ por $-150 \mathrm{m}/\mathrm{s}$. Negativo porque va hacia el oeste.

${\mathrm{sec}}^{2}\theta \frac{d\theta }{dt}=-\frac{1200}{{x}^{2}}\left(-150\right)$

${\mathrm{sec}}^{2}\theta \frac{d\theta }{dt}=\frac{180000}{{x}^{2}}$

Despejamos la variación del ángulo:

$\frac{d\theta }{dt}=\frac{180000}{{x}^{2}{\mathrm{sec}}^{2}\theta }=\frac{180000{\mathrm{cos}}^{2}\theta }{{x}^{2}}$

Podemos sustituir al coseno a partir del triángulo rectángulo.

$\mathrm{cos}\theta =\frac{x}{\sqrt{{x}^{2}+{1200}^{2}}}$

Sustituimos.

$\frac{d\theta }{dt}=\frac{180000}{{x}^{2}}\frac{{x}^{2}}{{x}^{2}+{1200}^{2}}$

Finalmente:

$\frac{d\theta }{dt}=\frac{180000}{{x}^{2}+{1200}^{2}}$

Concluimos entonces que la respuesta correcta es el inciso b).

Reactivo 13

Calcule el siguiente límite aplicando el teorema de L´Hopital para la resolución de límites.

$\underset{x\to 2}{\mathrm{lim}}\frac{2-\sqrt[3]{2{x}^{2}}}{{x}^{2}-4}$

1. $l=\frac{1}{6}$
2. $l=-\frac{1}{6}$
3. $l=1$

Solución:

Una de las aplicaciones más interesantes de las derivadas, es el teorema de L’Hopital que nos permite resolver límites, sin importar que tan complejos sean, aplicando de forma consecutiva derivadas en el numerador y el denominador hasta romper la indeterminación.

Comencemos por comprobar la indeterminación del límite dado.

$\underset{x\to 2}{\mathrm{lim}}\frac{2-\sqrt[3]{2{x}^{2}}}{{x}^{2}-4}=\frac{2-\sqrt[3]{2{\left(2\right)}^{2}}}{{\left(2\right)}^{2}-4}=\frac{0}{0}$

La indeterminación es cero dividido cero. Procedemos a derivar el numerador y al denominador una primera vez.

$\underset{x\to 2}{\mathrm{lim}}\frac{\frac{d}{dx}\left(2-\sqrt[3]{2{x}^{2}}\right)}{\frac{d}{dx}\left({x}^{2}-4\right)}=\underset{x\to 2}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{-\frac{2}{3}\sqrt[3]{2}{x}^{-\frac{1}{3}}}{2x}$

Simplificamos algebraicamente la expresión resultante.

$\underset{x\to 2}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{-\frac{2}{3}\sqrt[3]{2}{x}^{-\frac{1}{3}}}{2x}=\underset{x\to 2}{\mathrm{l}\mathrm{i}\mathrm{m}}\left(-\frac{\sqrt[3]{2}}{3}{x}^{-\frac{4}{3}}\right)$

Evaluamos nuevamente.

$\underset{x\to 2}{\mathrm{l}\mathrm{i}\mathrm{m}}\left(-\frac{\sqrt[3]{2}}{3}{x}^{-\frac{4}{3}}\right)=-\frac{\sqrt[3]{2}}{3}{\left(2\right)}^{-\frac{4}{3}}=-\frac{{2}^{-1}}{3}=-\frac{1}{6}$

$l=\underset{x\to 2}{\mathrm{lim}}\frac{2-\sqrt[3]{2{x}^{2}}}{{x}^{2}-4}=-\frac{1}{6}$

Comparando con las opciones, seleccionamos como respuesta correcta al inciso b).

Reactivo 14

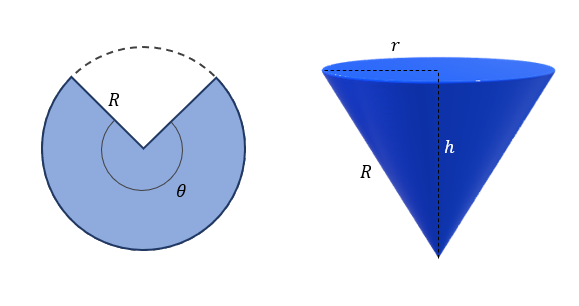
A partir de una lámina metálica circular se desea construir un cono. Para ello, se recorta un sector circular para luego doblarlo y formar el cono. Calcule el ángulo central $\theta$ que permite obtener el mayor volumen del cono.

1. $\theta =2\pi \sqrt{\frac{2}{3}} \mathrm{r}\mathrm{a}\mathrm{d}$
2. $\theta =2\pi  \mathrm{r}\mathrm{a}\mathrm{d}$
3. $\theta =0 \mathrm{r}\mathrm{a}\mathrm{d}$

Solución:

Comencemos por recordar cuál es la ecuación del volumen de un cono.

$V=\frac{1}{3}\pi {r}^{2}h$

Ahora, debemos dejar a dicha ecuación totalmente en función del ángulo $\theta$ y del radio del sector circular $R$. La primera relación que nos permitirá conectar la base del cono con la longitud del sector circular, son sus perímetros.

$2\pi r=R\theta$

Despejamos a $r$.

$r=\frac{\theta R}{2\pi }$

Aplicando el Teorema de Pitágoras en el triángulo que se forma en el cono, podemos despejar a la altura en función de $R$ y $\theta$.

${R}^{2}={r}^{2}+{h}^{2}\to h=\sqrt{{R}^{2}-{r}^{2}}$

Sustituimos a $r$.

$h=\sqrt{{R}^{2}-{\left(\frac{\theta R}{2\pi }\right)}^{2}}=R\sqrt{1-\frac{{\theta }^{2}}{4{\pi }^{2}}}$

Sustituimos todo en la ecuación del volumen.

$V=\frac{1}{3}\pi {\left(\frac{\theta R}{2\pi }\right)}^{2}\left(R\sqrt{1-\frac{{\theta }^{2}}{4{\pi }^{2}}}\right)$

Simplificamos y nos queda:

$V=\frac{{R}^{3}}{24{\pi }^{2}}{\theta }^{2}\sqrt{4{\pi }^{2}-{\theta }^{2}}$

Ya que necesitamos el máximo volumen en función del ángulo central, debemos derivar al volumen respecto de theta y luego igualar a cero. Tengamos en cuenta que el ángulo theta para la función está definido entre 0 y $2\pi$.

$\frac{dV}{d\theta }=\frac{d}{d\theta }\left(\frac{{R}^{3}}{24{\pi }^{2}}{\theta }^{2}\sqrt{4{\pi }^{2}-{\theta }^{2}}\right)$

$\frac{dV}{d\theta }=\frac{{\mathrm{R}}^{3}}{24{\pi }^{2}}\left[{\theta }^{2}\frac{-\theta }{\sqrt{4{\pi }^{2}-{\theta }^{2}}}+2\theta \sqrt{4{\pi }^{2}-{\theta }^{2}}\right]=\frac{{\mathrm{R}}^{3}}{24{\pi }^{2}}\left[-\frac{\theta \left(3{\theta }^{2}-8{\pi }^{2}\right)}{\sqrt{4{\pi }^{2}-{\theta }^{2}}}\right]$

Igualamos a cero y encontramos los puntos críticos entre 0 y $2\pi$.

$\frac{{\mathrm{R}}^{3}}{24{\pi }^{2}}\left[-\frac{\theta \left(3{\theta }^{2}-8{\pi }^{2}\right)}{\sqrt{4{\pi }^{2}-{\theta }^{2}}}\right]=0$

$\theta \left(3{\theta }^{2}-8{\pi }^{2}\right)=0$

De esta igualdad obtenemos que los puntos críticos son:

$\theta =0;\theta =2\pi \sqrt{\frac{2}{3}}$

No hemos tomado en cuenta el valor negativo de la raíz porque no pertenece al intervalo de existencia definido anteriormente. Por otra parte, $2\pi$ es equivalente a 0 radiantes.

No vamos a comprobar dichos valores en la función, porque uno corresponde a que el sector circular es realmente un círculo y el otro a que no existe el sector circular. Sustituimos entonces $\theta =2\pi \sqrt{\frac{2}{3}}$ en la función de volumen.

$V\left(2\pi \sqrt{2/3}\right)=\frac{{R}^{3}}{24{\pi }^{2}}(2\pi \sqrt{2/3}{)}^{2}\sqrt{4{\pi }^{2}-(2\pi \sqrt{2/3}{)}^{2}}=\frac{2\sqrt{3}\pi }{27}{R}^{3}$

El volumen máximo es ${V}_{max}=\frac{2\sqrt{3}\pi }{27}{R}^{3}$ y se alcanza cuando el ángulo central es $\theta =2\pi \sqrt{\frac{2}{3}}\approx 146.7°$.

Concluimos entonces que la respuesta correcta es el inciso a).

Reactivo 15

Hallar los números críticos de la siguiente función:

$f\left(x\right)=\sqrt[3]{{x}^{2}-2x}$

1. $x=1$
2. $x=0,  x=2$
3. $x=0, x=1 y x=2$

Solución:

Los números críticos de una función, son aquellos valores de la variable independiente en los que la pendiente de la recta tangente a la función en dicho punto vale cero o no se encuentra definida. Geométricamente hablando, esto puede significar que en ese número crítico la función tiene un máximo o un mínimo relativo.

Procedemos a encontrar la derivada de la función.

${f}^{\text{'}}\left(x\right)={\left(\sqrt[3]{{x}^{2}-2x}\right)}^{\text{'}}=\frac{1}{3}{\left({x}^{2}-2x\right)}^{-\frac{2}{3}}\left(2x-2\right)$

Simplificando nos queda:

${f}^{\text{'}}\left(x\right)=\frac{1}{3}{\left({x}^{2}-2x\right)}^{-\frac{2}{3}}\left(2x-2\right)=\frac{2}{3}\frac{x-1}{{\left({x}^{2}-2x\right)}^{\frac{2}{3}}}$

Igualamos la derivada a cero.

$\frac{2}{3}\frac{x-1}{{\left({x}^{2}-2x\right)}^{\frac{2}{3}}}=0\to x-1=0$

$\therefore x=1$

La función tiene un número crítico en $x=1$. Ahora, queda determinar los puntos en los que ${f}^{\text{'}}\left(x\right)$ no está definida. Esto sucede cuando el denominador se hace cero.

${\left({x}^{2}-2x\right)}^{\frac{2}{3}}=0\to {x}^{2}-2x=0$

Esto se cumple para $x=0$ y $x=2$. Concluimos entonces que los números críticos de la función son:

$x=0, x=1 y x=2$

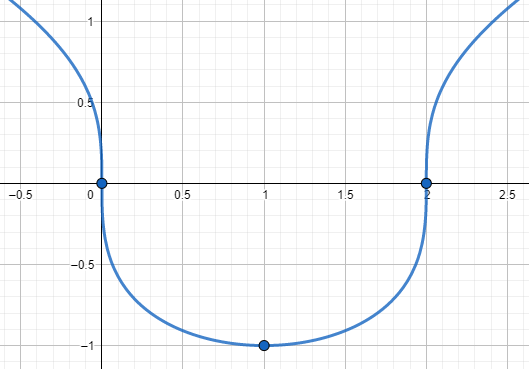
Comparando con las opciones, indicamos como correcta la opción c).

Reactivo 16

A partir del siguiente procedimiento para calcular la integral indefinida, diga cuales son los pasos en los que se ha cometido un error. Justifique su respuesta en cada caso.

Integral.

$\int \frac{dx}{1+\mathrm{cos}x}$

1. $\int \frac{1}{1} dx+\int \frac{dx}{\mathrm{cos}x}$
2. $x+\int \mathrm{sec}xdx$
3. $x+x\mathrm{sec}x\mathrm{tan}x+C$

 

1. 1 y 2
2. 2 y 3
3. 1 y 3

Solución:

En este caso, no vamos a resolver toda la integral para identificar cual o cuales son los pasos en los que se ha cometido algún error, porque es casi evidente. En el paso (1) se comete un grave error al separar la fracción en la suma de 1 y $\frac{1}{\mathrm{cos}x}$. Si la resolvemos, nos daremos cuenta de que no llegamos a la expresión inicial.

$1+\frac{1}{\mathrm{cos}x}=\frac{\mathrm{cos}x+1}{\mathrm{cos}x}$

Por tanto:

$1+\frac{1}{\mathrm{cos}x}\ne \frac{1}{1+\mathrm{cos}x}$

A partir de este punto, se vuelve a cometer otro error en el paso (3), ya que la integral de la $\mathrm{sec}x$ no es $x\mathrm{sec}x\mathrm{tan}x$ sino $\mathrm{sec}x\mathrm{tan}x$. Finalizado el análisis de la solución, concluimos entonces que los pasos con errores son: (1) y (3). Seleccionamos como respuesta correcta la opción c).

Reactivo 17

En base a la teoría fundamental sobre las integrales indefinidas, ¿por qué se coloca la c al integrar y cuál es su interpretación geométrica?

1. Para seleccionar cualquier curva
2. Porque es necesario para que se cumpla la igualdad
3. Porque la integral indefinida representa una familia de antiderivadas, expresadas como una familia de curvas

Solución:

Cuando integramos indefinidamente a una función $f$, realmente estamos obteniendo a una familia de antiderivadas de dicha función. Para cada valor real de la constante $c$ obtenemos a un miembro de la familia.

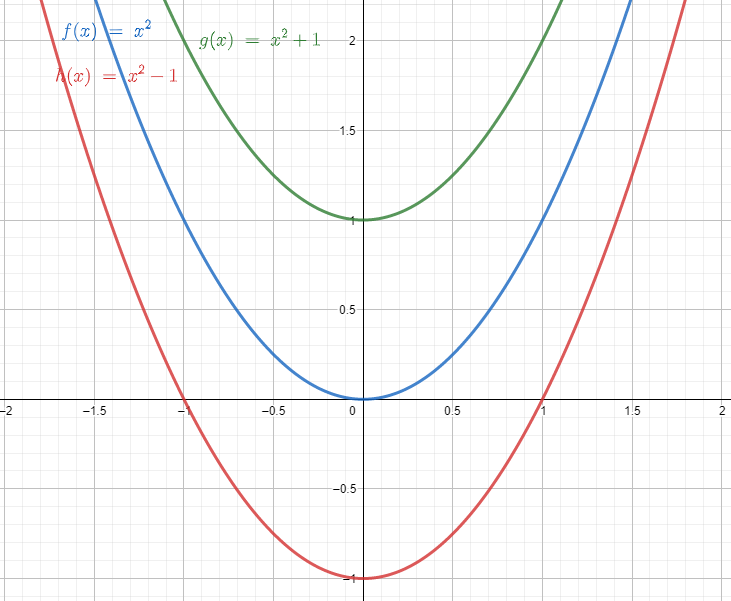
En términos geométricos, la familia se representa por un conjunto de curvas paralelas unas a otras, de tal forma que al derivar cualquiera de ellas, se obtiene la función original. La imagen anterior representa a la familia $y={x}^{2}+c$.

De esta manera, si $F\left(x\right)={x}^{2}+c$ al derivarla obtenemos $f\left(x\right)=2x$.

En base a todo nuestro análisis, concluimos que la respuesta correcta es la opción c).

Reactivo 18

Demuestre que la integral de cualquier función $f\left(x\right)={x}^{n}$ para todo $n\ne -1$ es $F\left(x\right)=\frac{1}{n+1}{x}^{n+1}+c$.

1. $F\left(x\right)=\int {x}^{n}dx=\frac{{x}^{n+1}}{n+1}+c$
2. $F\left(x\right)=\int {x}^{n}dx=\frac{{x}^{n}}{n+1}+c$
3. $F\left(x\right)=\int {x}^{n}dx=\frac{{x}^{n+1}}{n}+c$

Solución:

Iniciamos por colocar a nuestra función en el operador de integración.

$F\left(x\right)=\int {x}^{n}dx$

Ahora, sabemos que, al derivar a la variable elevada a una potencia bajamos el exponente para que multiplique a la función y luego se le resta uno a dicho exponente. Por ejemplo:

$\frac{d}{dx}\left({x}^{4}\right)=4{x}^{4-1}=4{x}^{3}$

De esta forma, nos damos cuenta que si queremos regresarnos, es decir antiderivar, debemos sumar uno al nuevo exponente de la variable y dividir a la misma por dicho valor.

$F\left(x\right)=\frac{4{x}^{3+1}}{3+1}=\frac{4}{4}{x}^{4}={x}^{4}$

Si ahora nos vamos al caso general y tomamos al exponente como $n$, para antiderivas a ${x}^{n}$ debemos sumar uno al exponente y dividir por dicho valor.

$F\left(x\right)=\int {x}^{n}dx=\frac{{x}^{n+1}}{n+1}+c$

Si derivamos el resultado, tendríamos que obtener la función original.

$\frac{d}{dx}F\left(x\right)={\left(\frac{{x}^{n+1}}{n+1}+c\right)}^{\text{'}}=\frac{n+1}{n+1}{x}^{n+1-1}+0={x}^{n}$

Así, hemos demostrado que la integral de $f\left(x\right)={x}^{n}$ es $\frac{{x}^{n+1}}{n+1}+c$ siempre que $n\ne 1$.

Concluimos que la respuesta correcta es la a).

Reactivo 19

Resuelva la siguiente integral aplicando artificios matemáticos.

$\int \left(\frac{3}{\sqrt[4]{t}}-{2}^{t}\right)dt$

1. $4{t}^{\frac{3}{4}}-\frac{{2}^{t}}{\mathrm{ln}2}+C$
2. $-\frac{{2}^{t}}{\mathrm{ln}2}+C$
3. $4{t}^{\frac{3}{4}}+C$

Solución:

Iniciamos aplicando la propiedad de la integral de la suma.

$\int \left(\frac{3}{\sqrt[4]{t}}-{2}^{t}\right)dt=\int \frac{3}{\sqrt[4]{t}}dt-\int {2}^{t}dt$

Extraemos la constante de la integral y aplicamos la propiedad del exponente negativo al primer término.

$\int \frac{3}{\sqrt[4]{t}}dt-\int {2}^{t}dt=3\int {t}^{-\frac{1}{4}}dt-\int {2}^{t}dt$

Con todo acomodado, solo nos queda identificar las fórmulas de integración que debemos aplicar. Para el primer término será la fórmula de la integral de la potencia y para la segunda la fórmula de una función exponencial.

$3\int {t}^{-\frac{1}{4}}dt-\int {2}^{t}dt=\frac{3}{1-\frac{1}{4}}{t}^{1-\frac{1}{4}}-\frac{1}{\mathrm{ln}2}{2}^{t}+C$

Simplificamos.

$=\frac{3}{1-\frac{1}{4}}{t}^{1-\frac{1}{4}}-\frac{1}{\mathrm{ln}2}{2}^{t}+C=4{t}^{\frac{3}{4}}-\frac{{2}^{t}}{\mathrm{ln}2}+C$

Finalmente.

$\int \left(\frac{3}{\sqrt[4]{t}}-{2}^{t}\right)dt=4{t}^{\frac{3}{4}}-\frac{{2}^{t}}{\mathrm{ln}2}+C$

Concluimos indicando como respuesta correcta la opción a).

Reactivo 20

Calcule la siguiente integral aplicando artificios matemáticos y las fórmulas correspondientes.

$\int \frac{dx}{1+\mathrm{cos}x}$

1. $\mathrm{csc}x+C$
2. $-\mathrm{cot}x+\mathrm{csc}x+C$
3. $-\mathrm{tan}x+\mathrm{csc}x+C$

solución:

Es claro que no podemos aplicar directamente ninguna fórmula de integración directa, es necesario trabajar el integrando. Comencemos por multiplicar y dividir por $1-\mathrm{cos}x$.

$\int \frac{\left(1-\mathrm{cos}x\right)dx}{\left(1+\mathrm{cos}x\right)\left(1-\mathrm{cos}x\right)}=\int \frac{\left(1-\mathrm{cos}x\right)dx}{1-{\mathrm{cos}}^{2}x}$

Por la identidad pitagórica sustituimos al denominador.

$\int \frac{\left(1-\mathrm{cos}x\right)dx}{{\mathrm{sin}}^{2}x}=\int \frac{1}{{\mathrm{sin}}^{2}x}dx-\int \frac{\mathrm{cos}x}{{\mathrm{sin}}^{2}x}dx$

Separamos $\frac{\mathrm{cos}x}{{\mathrm{sin}}^{2}x}$ como $\frac{\mathrm{cos}x}{\mathrm{sin}x}\bullet \frac{1}{\mathrm{sin}x}$ y sustituimos $\frac{1}{{\mathrm{sin}}^{2}x}$ por ${\mathrm{csc}}^{2}x$.

$\int \frac{1}{{\mathrm{sin}}^{2}x}dx-\int \frac{\mathrm{cos}x}{{\mathrm{sin}}^{2}x}dx=\int {\mathrm{csc}}^{2}xdx-\int \frac{\mathrm{cos}x}{\mathrm{sin}x}\bullet \frac{1}{\mathrm{sin}x}dx$

$\int {\mathrm{csc}}^{2}xdx-\int \frac{\mathrm{cos}x}{\mathrm{sin}x}\bullet \frac{1}{\mathrm{sin}x}dx=\int {\mathrm{csc}}^{2}xdx-\int \mathrm{cot}x\mathrm{csc}xdx$

Aplicamos las fórmulas de la integral de la cosecante cuadrado y de la cotangente por la cosecante.

$\int {\mathrm{csc}}^{2}xdx-\int \mathrm{cot}x\mathrm{csc}xdx=-\mathrm{cot}x+\mathrm{csc}x+C$

Finalmente:

$\int \frac{dx}{1+\mathrm{cos}x}=-\mathrm{cot}x+\mathrm{csc}x+C$

Concluimos que la respuesta correcta es la opción b).