La Circunferencia, es una de las figuras geométricas básicas y una pieza fundamental en el mundo que nos rodea. Desde los neumáticos de los coches en los que te desplazas, hasta la forma que tienen los engranajes en cualquier máquina, ¡las circunferencias se encuentran en todos lados!

En este post, explicaremos los conceptos detrás de la circunferencia, definiendo sus partes y explicando detalladamente los ángulos y posiciones en ella. Dedicaremos una sección para discutir la diferencia entre círculo y circunferencia, para finalizar con ejercicios resueltos.
¿Qué es una circunferencia?
Es una línea curva cerrada conformada por un conjunto de puntos en un mismo plano, situados a la misma distancia de un punto fijo llamado centro de la circunferencia.
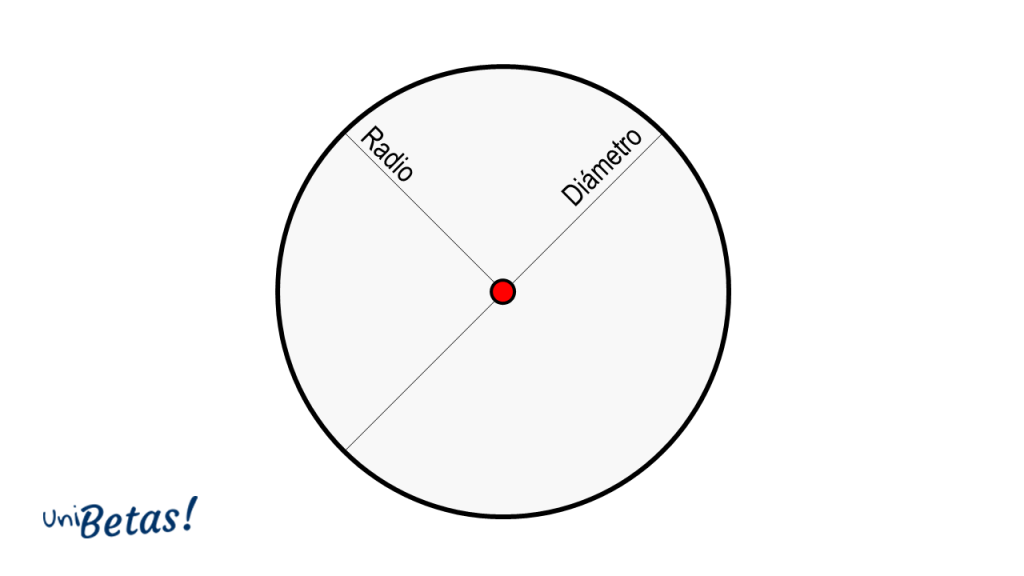
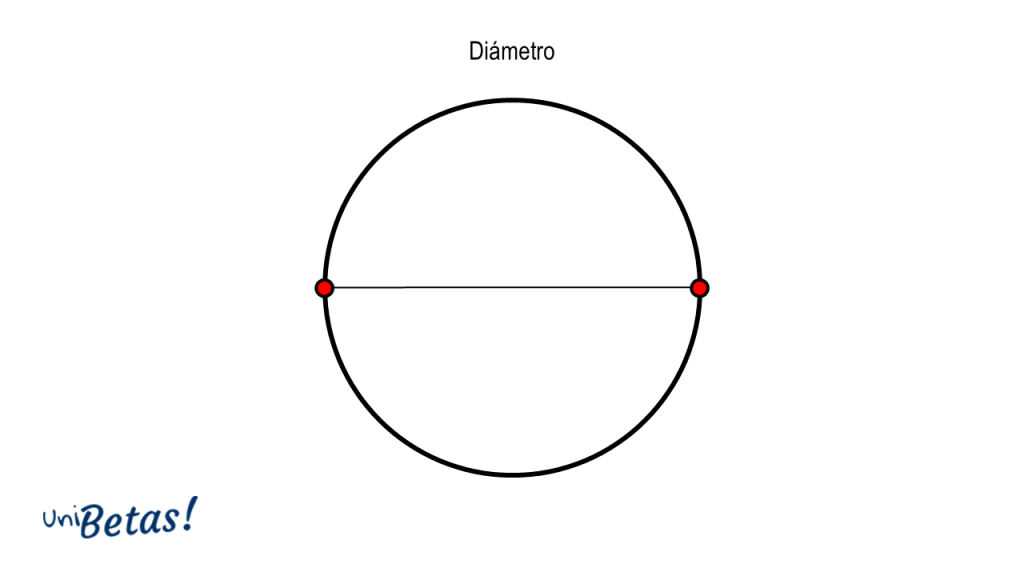
Esta distancia fija a la que se encuentran los puntos de la circunferencia se denomina radio de la circunferencia. Similar al radio, el diámetro es la distancia medida entre dos puntos opuestos en la circunferencia y cuya magnitud es igual al doble del radio.
d=2r
El diámetro posee otra característica importante. Pasa por el centro de la circunferencia y es la línea (también llamada cuerda, definición que veremos más adelante) de mayor longitud que se puede trazar dentro de una circunferencia.
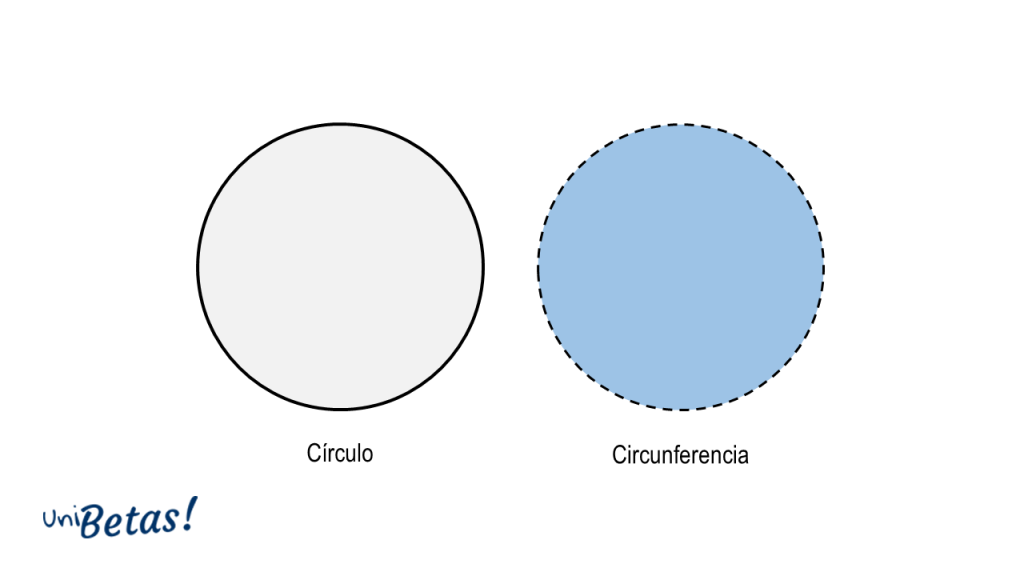
Círculo y Circunferencia
Existe una gran confusión respecto a estas dos figuras, muchas veces empleadas como sinónimos, que guardan grandes similitudes, pero una diferencia bastante importante: la circunferencia es el lugar geométrico y el círculo una región del plano.
La circunferencia es una línea curva cuyos puntos distan igual respecto del centro. Por otro lado, el círculo es una región de puntos, un área, una superficie cuyos puntos se encuentran a una distancia no mayor al radio respecto del centro.
Elementos de la Circunferencia
Dentro y fuera de la circunferencia, tienen lugar distintos elementos notables como rectas y puntos, que se emplean con frecuencia en los problemas tipo examen para incrementar su complejidad.
La necesidad de conocerlos, radica en dos cosas:
- Algunos datos cruciales pueden darse en términos de estos elementos notables
- Pueden ser útiles para llegar a la solución del problema
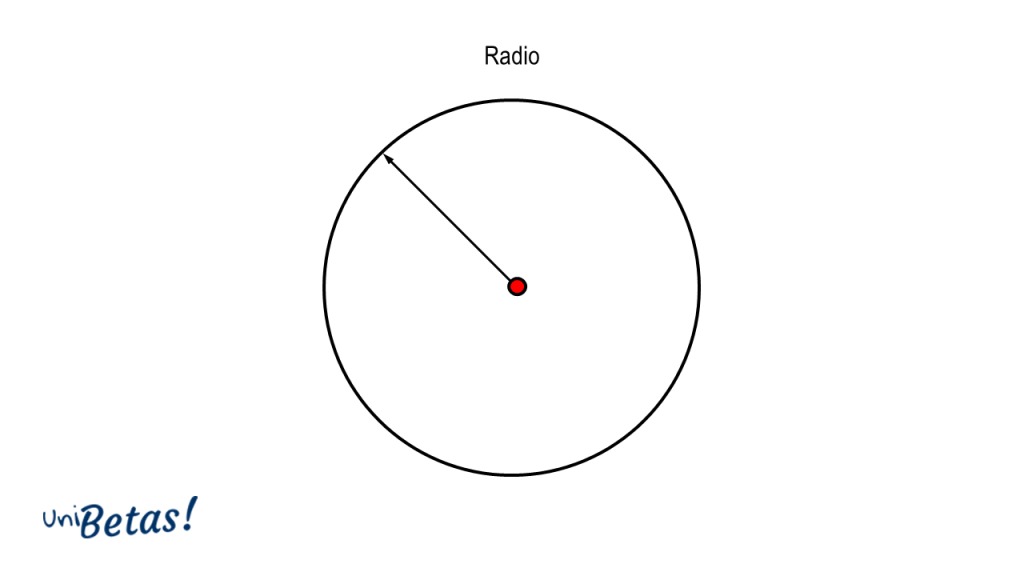
Radio de la circunferencia. Tal como se mencionó antes, es el segmento de recta que va desde el centro a cualquier punto de la circunferencia.
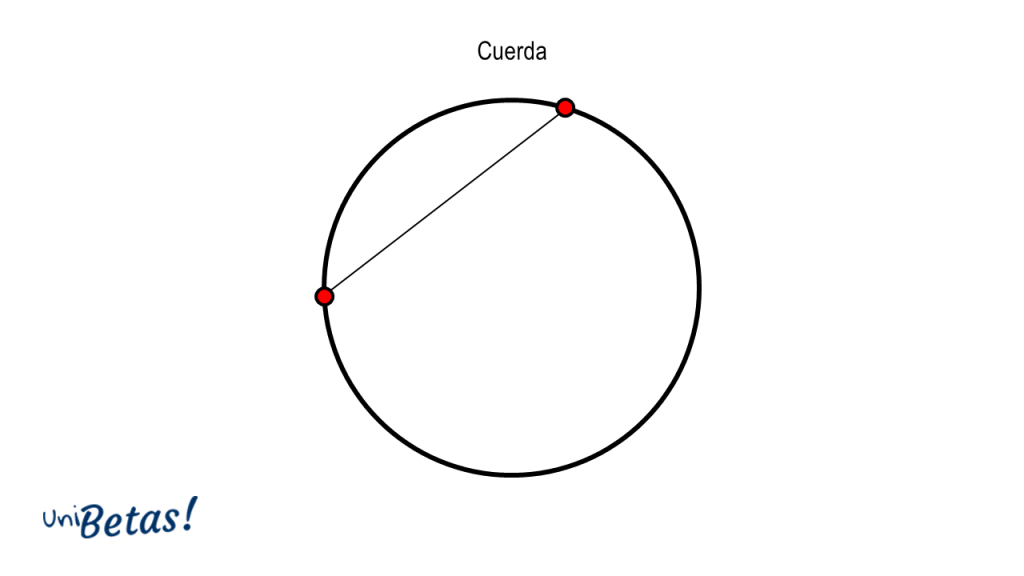
Cuerda. Se llama así, a todo segmento rectilíneo que une dos puntos de la circunferencia sin pasar por el centro.
Diámetro. Definido con anterioridad, es un segmento de recta que une dos puntos opuestos de la circunferencia y que, a su vez, pasa por el centro. Su magnitud es 2 veces la del radio.
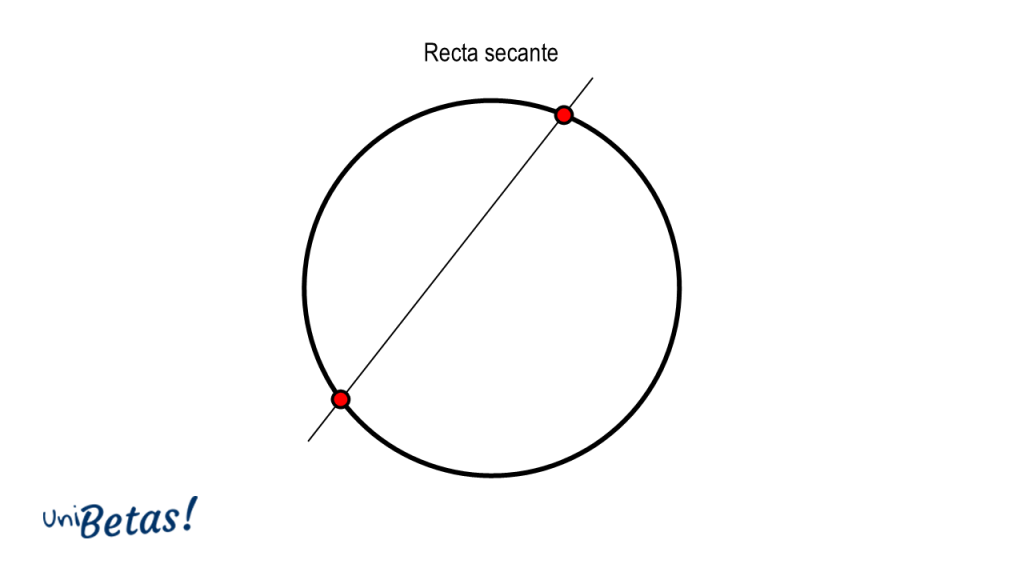
Secante. Es secante toda recta que pasa por dos puntos de la circunferencia. La diferencia con la cuerda, es que una secante tiene sus extremos prolongados.
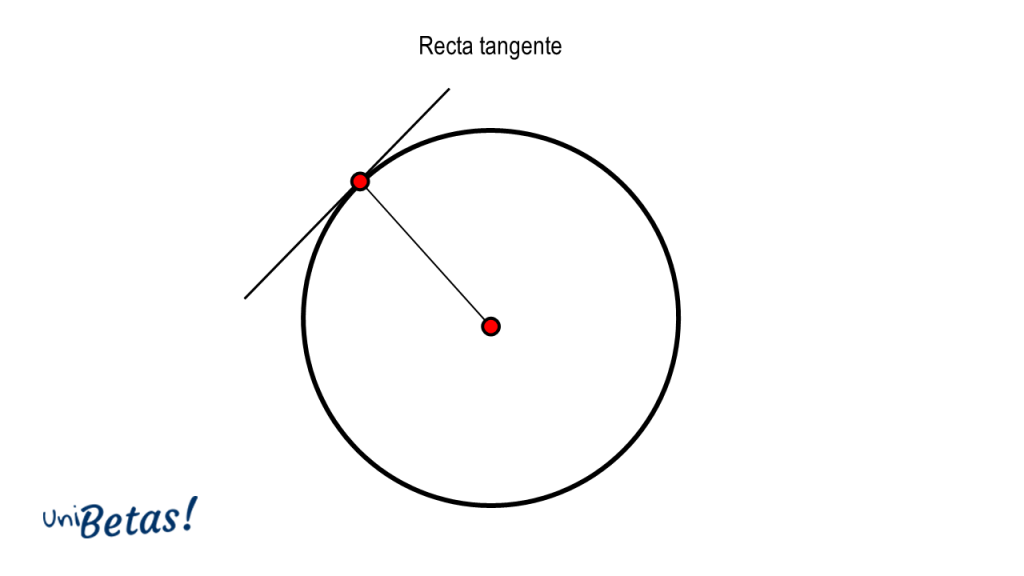
Tangente. Recta que pasa por un único punto de la circunferencia. Tiene la propiedad de ser perpendicular al radio trazado hacia el punto de tangencia.
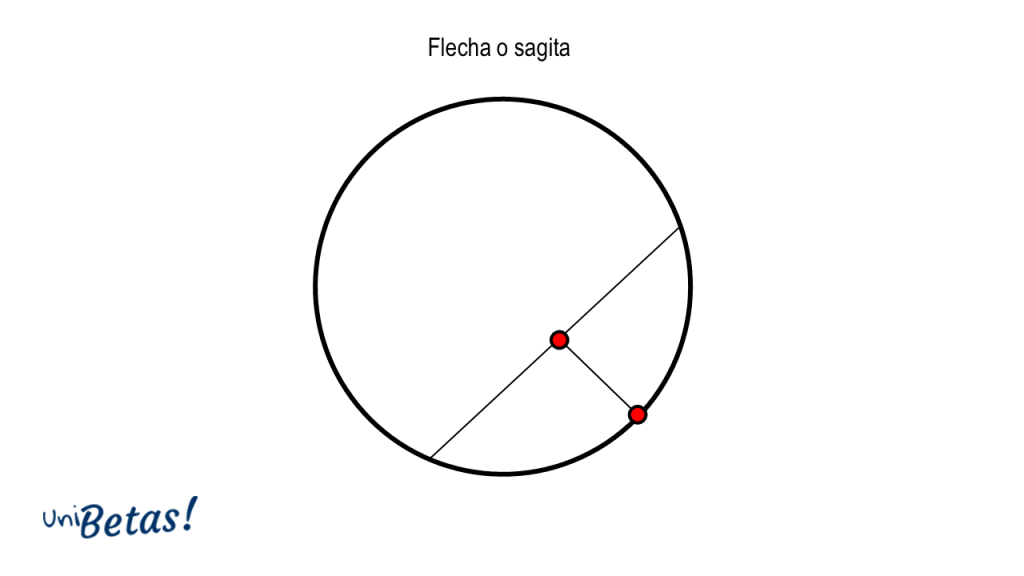
Flecha o sagita. Es segmento que se traza perpendicular a una cuerda hasta tocar un punto en la circunferencia.
Porciones de círculo
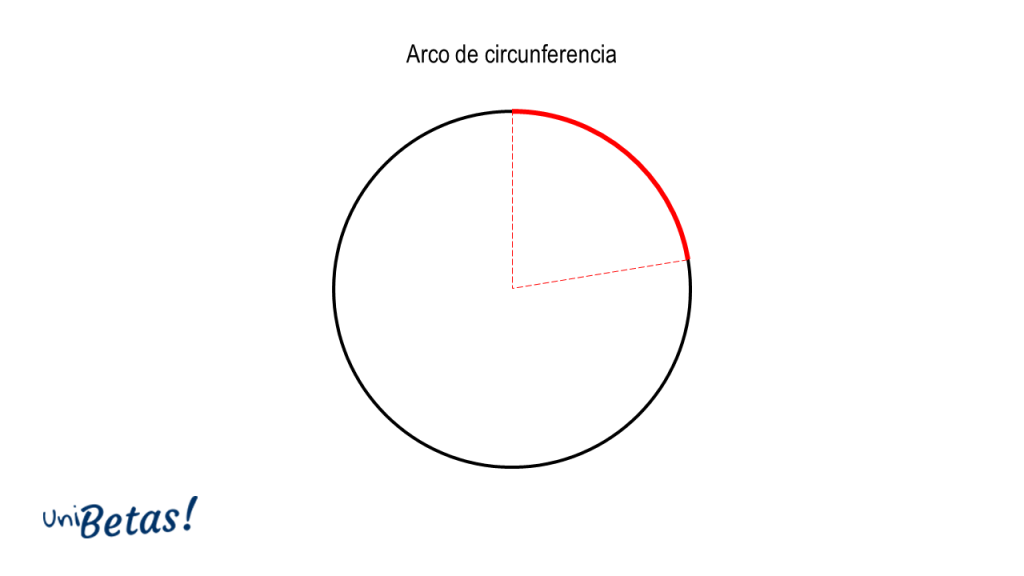
Arco de circunferencia. Es un sector de la circunferencia delimitado por dos radios y cuya apertura es igual al menor ángulo entre los radios.
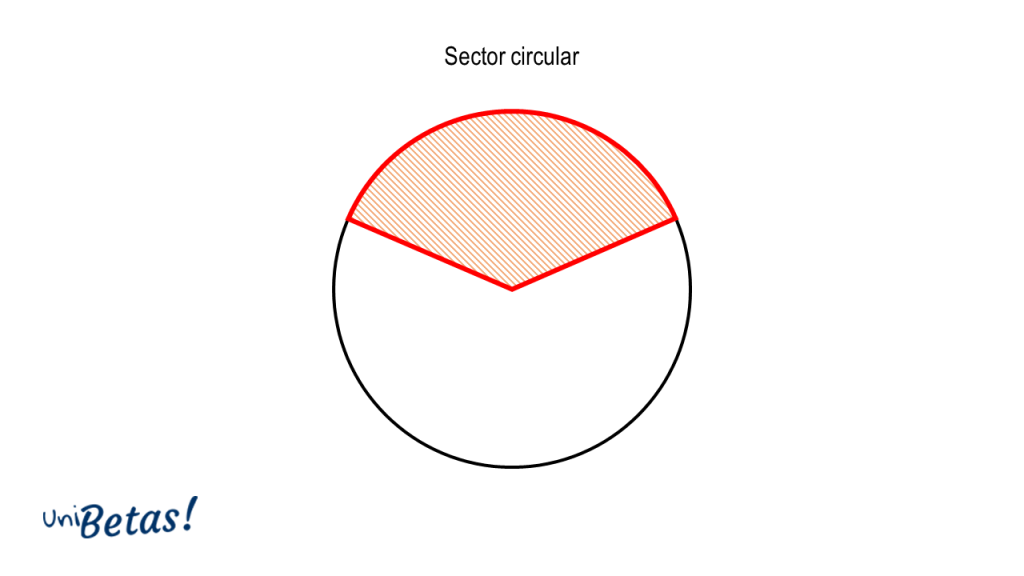
Sector circular. Es el área de círculo que se forma entre dos radios y el arco de circunferencia frente a ellas.
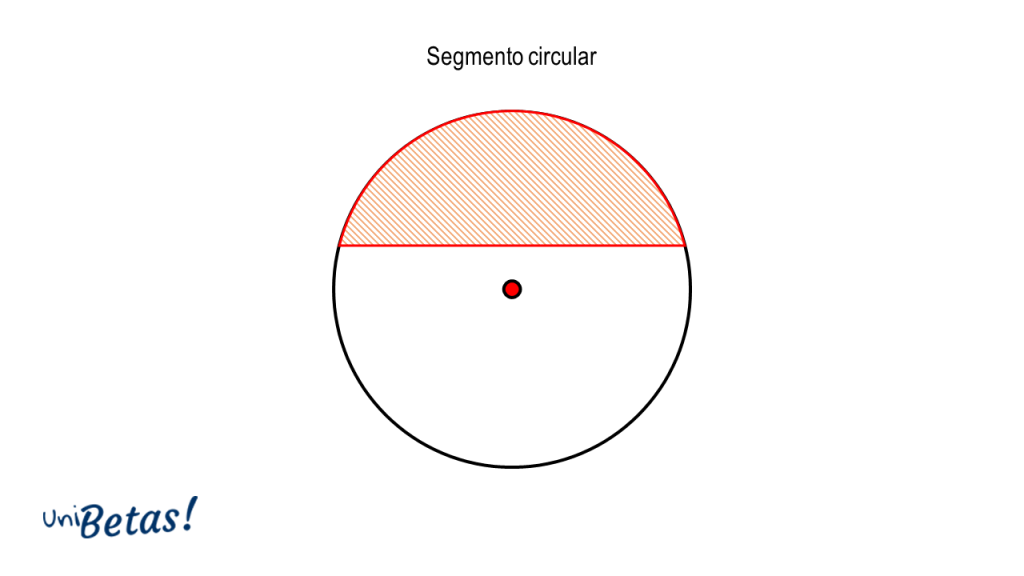
Segmento circular. Es la región formada entre una cuerda y el arco de circunferencia frente a ella.
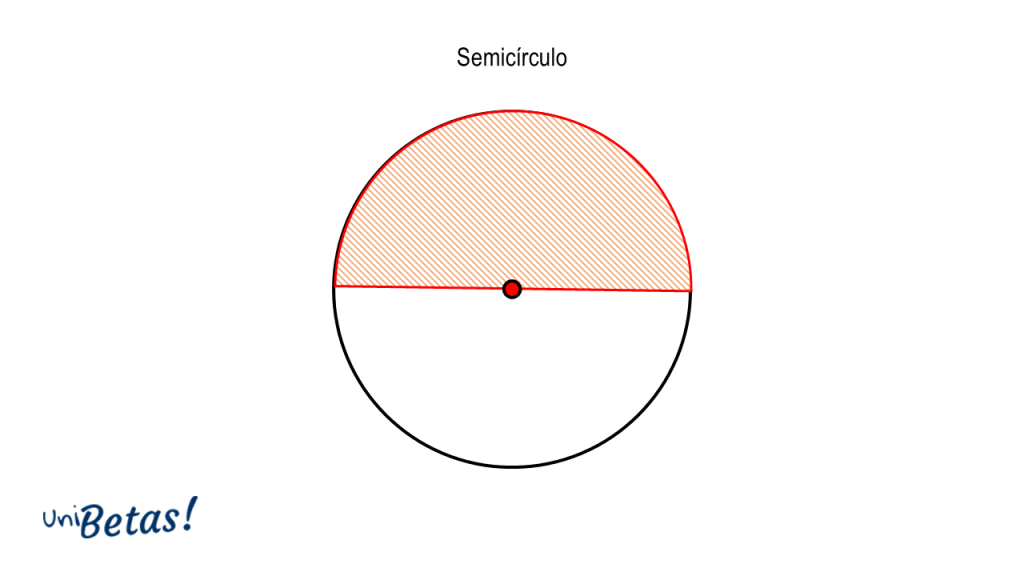
Semicírculo. Es el área delimitada por un diámetro en la circunferencia y cualquiera de las dos semicircunferencias que se establecen alrededor de ella.
Longitud de la circunferencia
Al igual que en un polígono regular, podemos medir el perímetro de la circunferencia a través de una fórmula matemática. Para ello, necesitamos conocer el radio o diámetro de la misma.
Perímetro de una circunferencia.
l=2\pi r
Área de un círculo
Por otro lado, podemos calcular el área que encierra una circunferencia mediante la siguiente fórmula:
Área encerrada por una circunferencia.
A=\pi {r}^{2}
Ángulos en la Circunferencia
Ahora, toca examinar algunos ángulos que se forman entre los distintos segmentos notables dentro y fuera de la circunferencia. Aprende a reconocerlos muy bien, ya que suelen ser el talón de Aquiles para muchos estudiantes durante los exámenes y eso los maestros lo saben muy bien.
Ángulo central. Es el ángulo formado entre dos radios de la circunferencia, también, entre un diámetro y un radio. El vértice del ángulo central es el centro de la circunferencia.
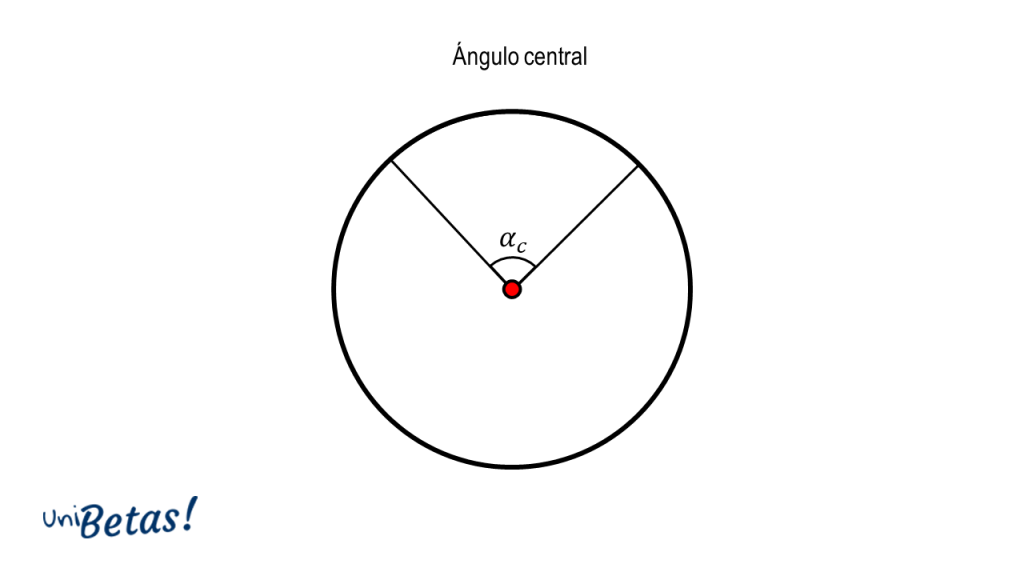
El ángulo central {\alpha }_{c} es igual al arco de circunferencia formado.
Ángulo inscrito. Es el ángulo formado entre dos cuerdas de la circunferencia que tienen un extremo en común y dicho extremo común es el vértice del ángulo inscrito.
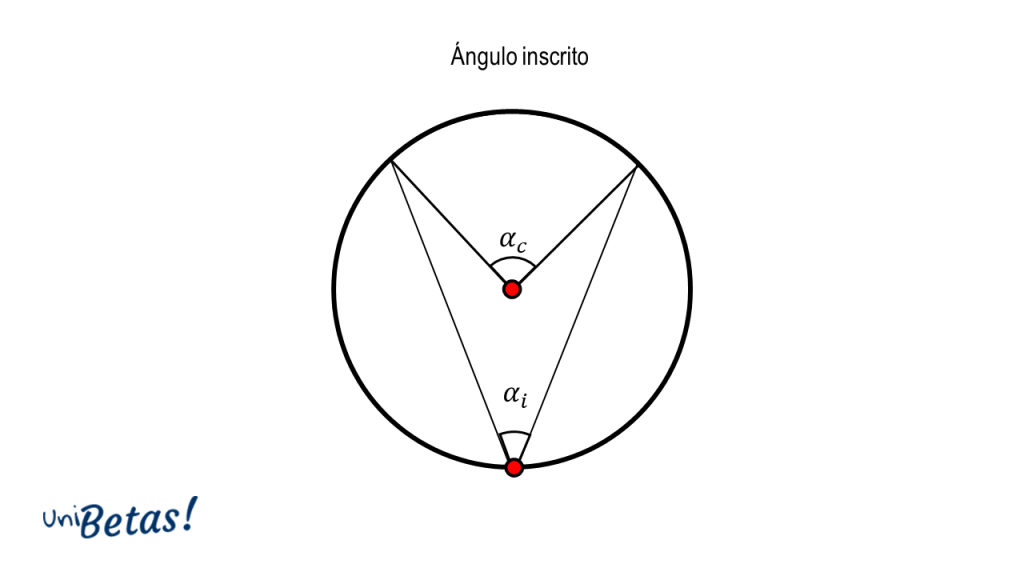
El ángulo inscrito {\alpha }_{i} es la mitad del ángulo central formado.
{\alpha }_{i}=\frac{{\alpha }_{c}}{2}
Ángulo semiinscrito. El vértice del ángulo se encuentra sobre la circunferencia y lo forman la intersección entre una cuerda y una secante.
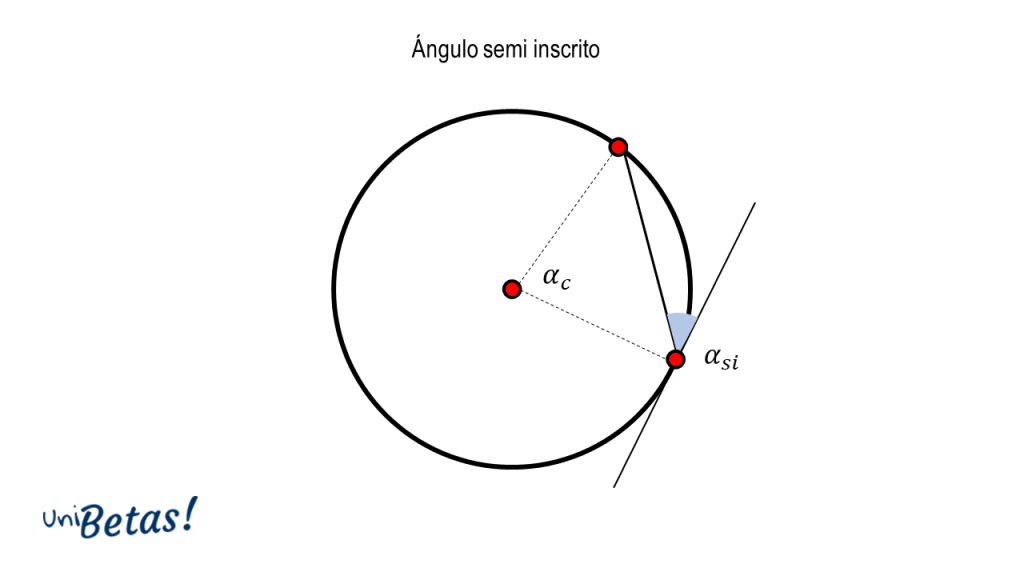
El ángulo semiinscrito {\alpha }_{si} es igual a la mitad del ángulo central entre los radios punteados.
{\alpha }_{si}=\frac{{\alpha }_{c}}{2}
Ángulo interior. Se forma en la intersección entre dos cuerdas dentro de la circunferencia. El vértice del ángulo interior es el punto de intersección entre las cuerdas.
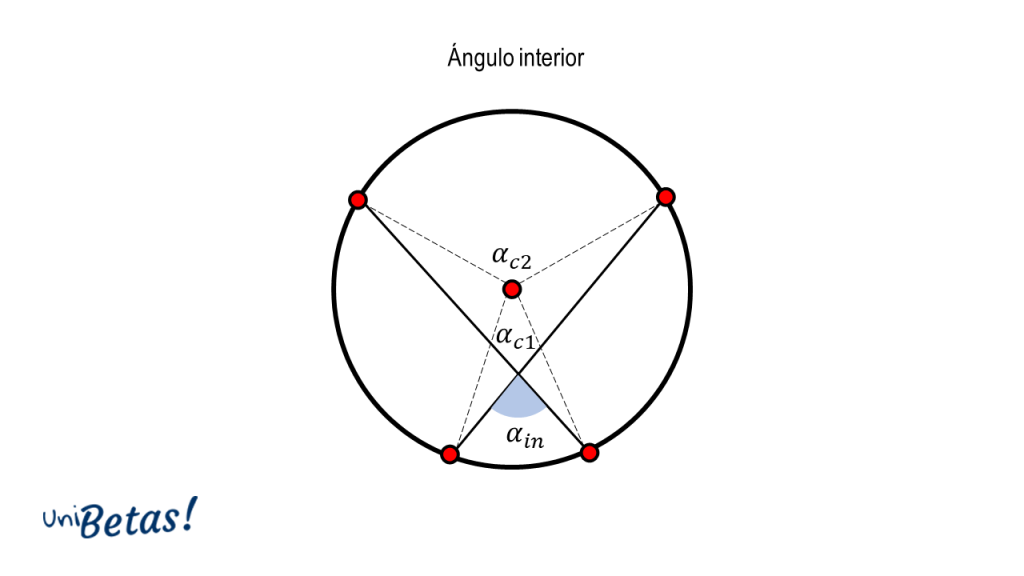
El ángulo interior {\alpha }_{in} es igual a la semisuma de los ángulos centrales formados.
{\alpha }_{in}=\frac{{\alpha }_{c1}+{\alpha }_{c2}}{2}
Ángulo exterior. Es el ángulo que tiene como vértice a un punto exterior a la circunferencia, el cual es la intersección entre dos rectas secantes a la circunferencia.
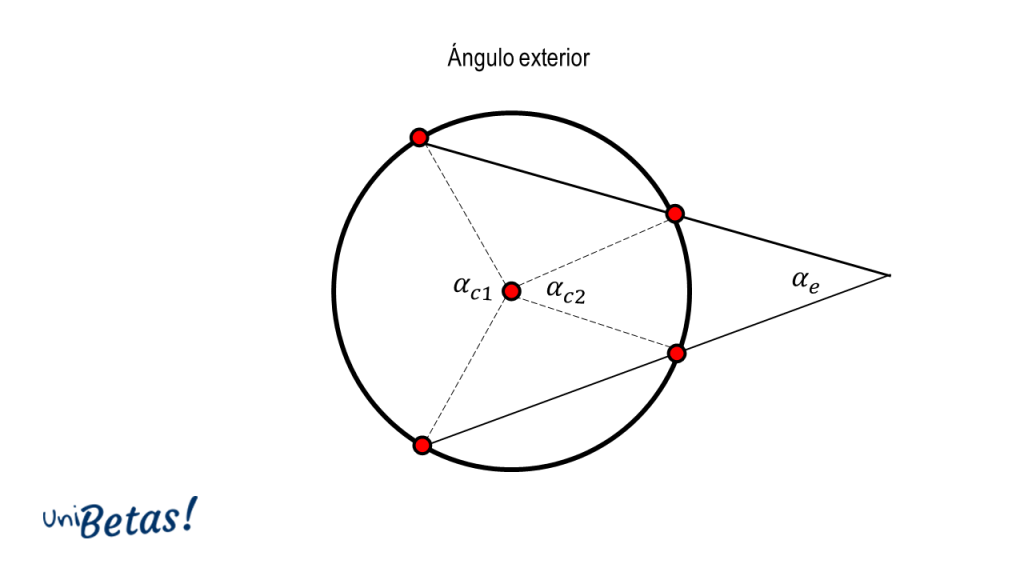
El ángulo exterior {\alpha }_{e} es igual a la semirrecta entre los ángulos centrales que se forman.
{\alpha }_{e}=\frac{{\alpha }_{c2}-{\alpha }_{c1}}{2}
Posiciones relativas de dos circunferencias
En esta sección, se estudian las posiciones que pueden tener dos circunferencias entre sí.
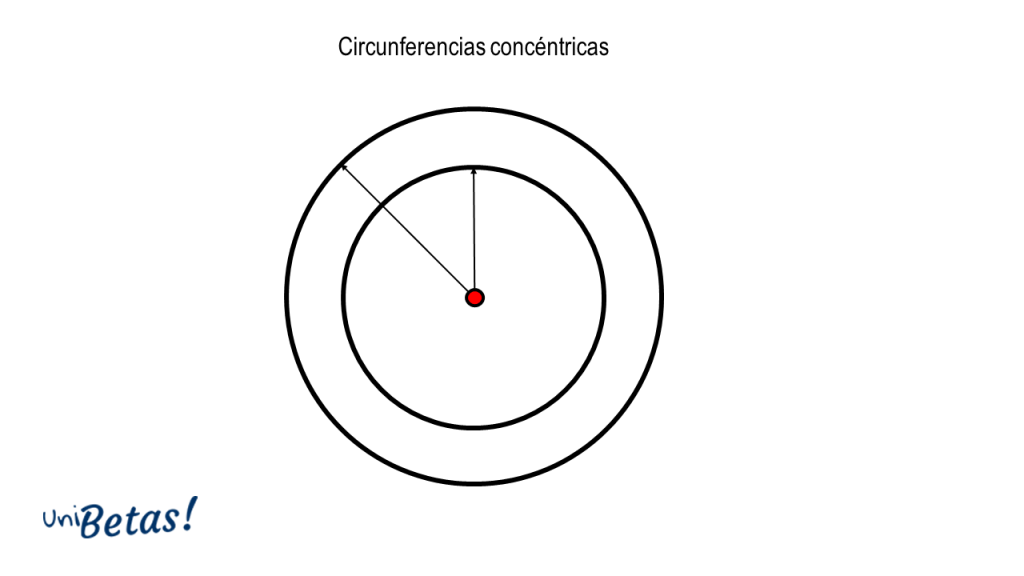
Circunferencias concéntricas. Son circunferencias con el mismo centro, pero distinto radio.
Circunferencias exteriores. Son aquel par de circunferencias donde la distancia entre sus centros es mayor que la suma de sus radios.
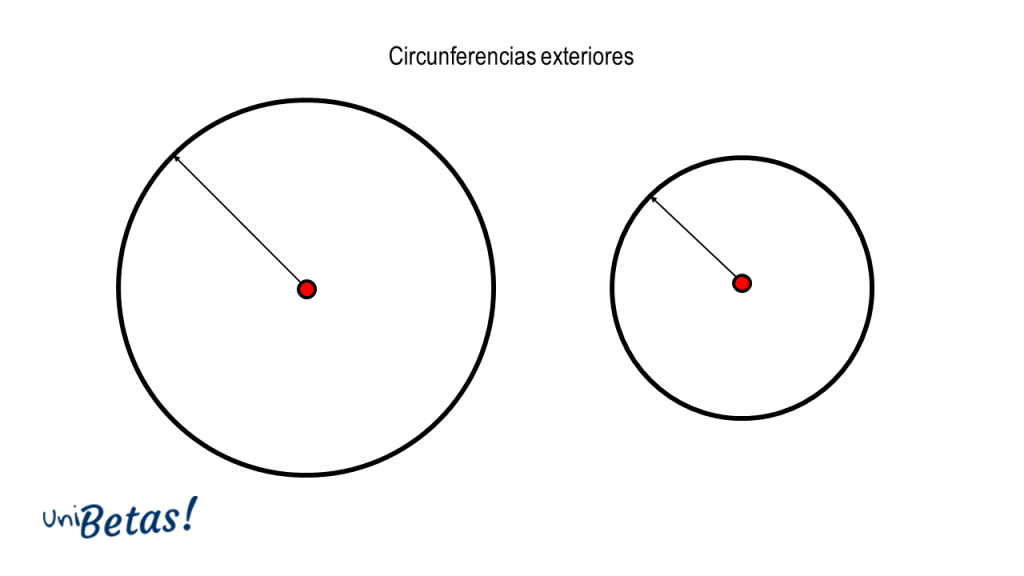
d\left({c}_{1},{c}_{2}\right)>{r}_{1}+{r}_{2}
Circunferencia interior. Se llama circunferencia interior, a una circunferencia {c}_{1} de radio {r}_{1} cuyos puntos se encuentran dentro de la región encerrada por otra circunferencia {c}_{2} de radio {r}_{2} . Donde se cumple que:
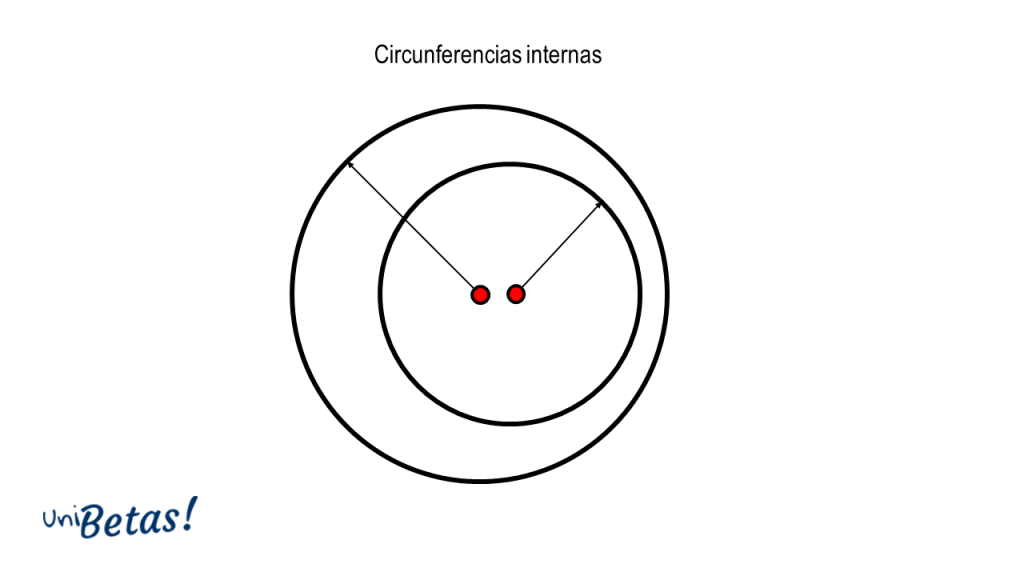
{r}_{2}>{r}_{1}
d\left({c}_{1},{c}_{2}\right)<{r}_{1}+{r}_{2}
Circunferencias tangentes. Se presenta cuando dos circunferencias se tocan en un único punto. La tangencia puede ser exterior, cuando los puntos de ambas circunferencias son mutuamente exteriores o interna, cuando los puntos de una de las circunferencias están dentro de la otra.
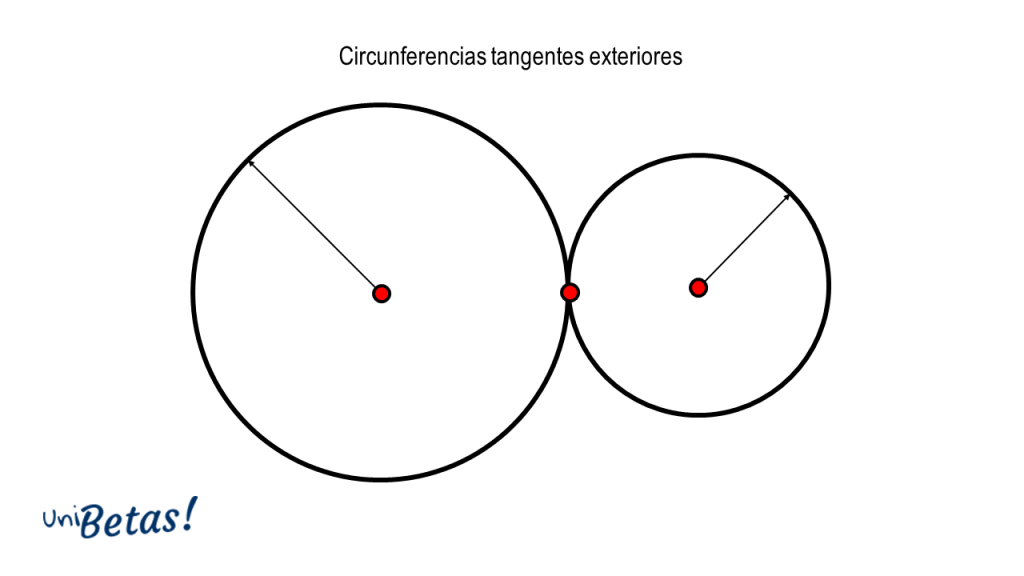
Tangentes exteriores.
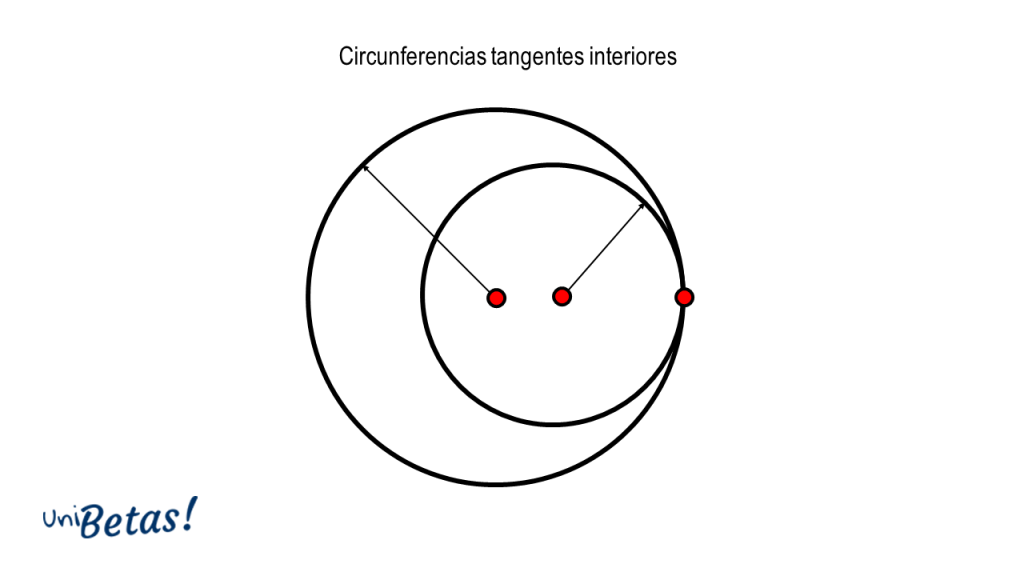
Tangente interior.
Circunferencias secantes. Son circunferencias que se tocan en dos puntos. En este caso, la distancia entre los centros es menor que la suma de los radios.
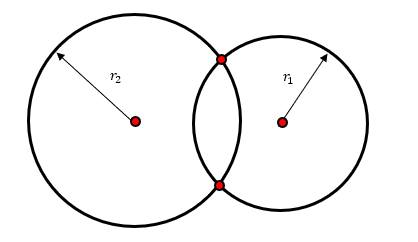
Un caso especial de circunferencias secantes, sucede cuando los radios son perpendiculares entre sí en los puntos de intersección. Se denominan entonces circunferencias ortogonales.
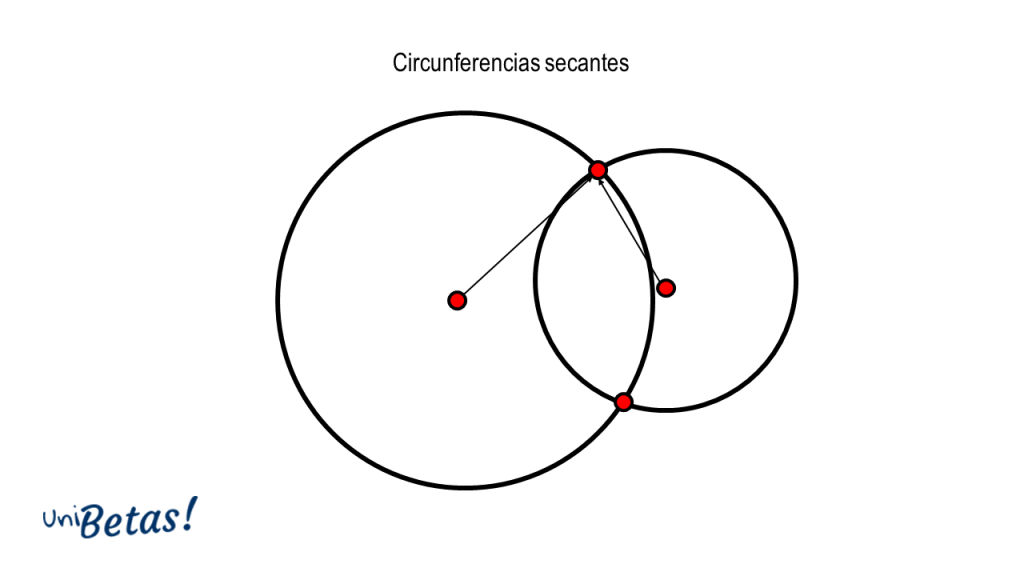
Se cumple que:
d\left({c}_{1},{c}_{2}\right)=\sqrt{{r}_{1}^{2}+{r}_{2}^{2}}
Elementos de la circunferencia ejercicios resueltos
Reactivo 1
En base a la situación planteada en la figura, ¿cuál es la distancia entre los puntos T y T’ en función del radio de la circunferencia?
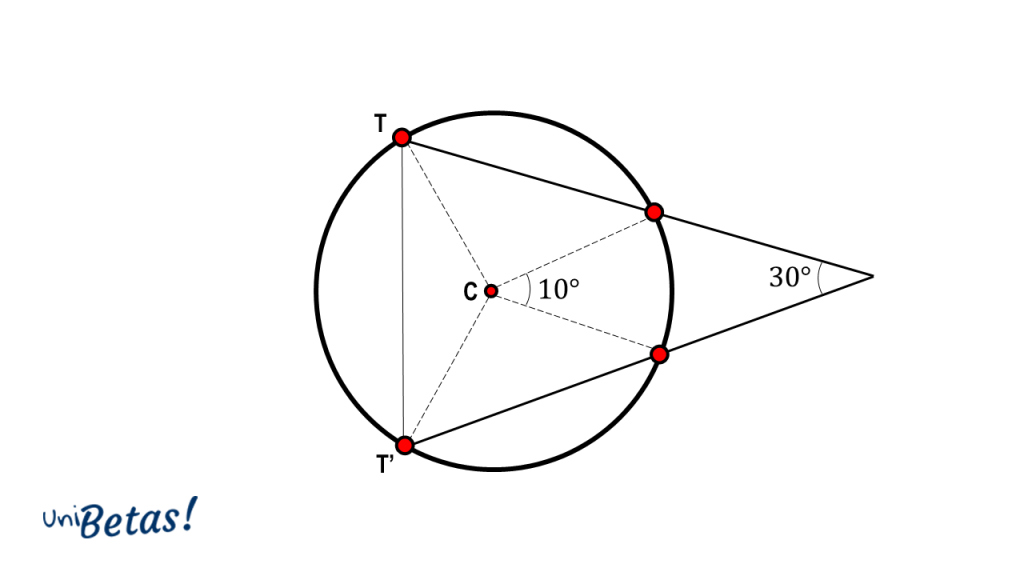
Solución:
Para calcular la distancia entre T y T\text{'} , debemos aplicar la ley de los cosenos la cual dice que:
T{T}^{\text{'}2}={R}^{2}+{R}^{2}-2RR\mathrm{cos}{\alpha }_{c1}
El ángulo {\alpha }_{c1} corresponde al ángulo central mayor de la circunferencia, el cuál podemos calcular aplicando la fórmula del ángulo exterior:
{\alpha }_{e}=\frac{{\alpha }_{c1}-{\alpha }_{c2}}{2}
Despejando:
{\alpha }_{c1}=2{\alpha }_{e}+{\alpha }_{c2}
Sustituimos el valor de ambos ángulos.
{\alpha }_{c1}=2\left(30°\right)+10°=70°
Sustituimos el ángulo en la primera ecuación.
T{T}^{\text{'}2}=2{R}^{2}-2{R}^{2}\mathrm{cos}70
T{T}^{\text{'}}=R\sqrt{2-2\mathrm{cos}70}=R\sqrt{2-0.684}=\sqrt{1.316}R
TT´=\sqrt{1.316}R
Reactivo 2
Calcule el área que encierran las dos circunferencias concéntricas.
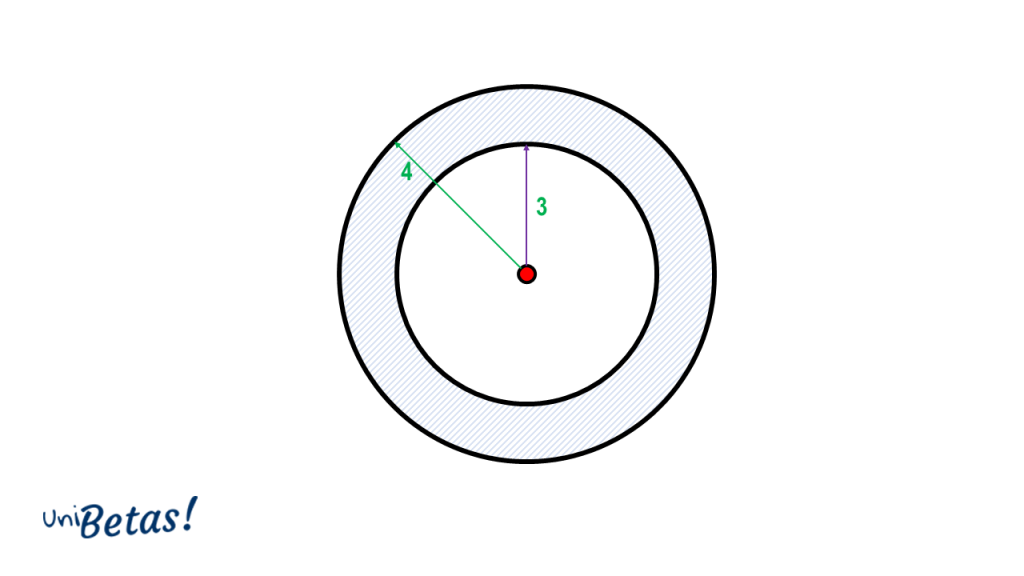
Solución:
El área que encierran ambas circunferencias se calcula como la resta del área menor al área mayor. La circunferencia de radio igual a 4 unidades encierra más área que la de radio 3 unidades, por tanto:
A=\pi {4}^{2}-\pi {3}^{2}=16\pi -9\pi =7\pi
El área entre las circunferencias es igual a 7\pi unidades cuadradas.
Reactivo 3
Para dos circunferencias secantes entre sí, ¿cuánto debe medir el radio de una de ellas para que se cumpla la ortogonalidad entre ellas? Sepa que: {r}_{1}=1 \mathrm{m} , d\left({r}_{1},{r}_{2}\right)=2 \mathrm{m} .
Solución:
Dos circunferencias son secantes entre ellas si se cortan en dos puntos, ahora para que dicha intersección sea ortogonal, sebe cumplirse además que:
d{\left({r}_{1},{r}_{2}\right)}^{2}={r}_{1}^{2}+{r}_{2}^{2}
Es decir, que se forme un triángulo rectángulo entre los radios y la distancia entre ellos. En este caso, tenemos la distancia entre los centros y el radio {r}_{1} , despejamos a {r}_{2} .
{r}_{2}=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}
Concluimos que: para que la intersección sea ortogonal, el radio de la segunda circunferencia debe ser \sqrt{3} metros.


