El teorema de Pitágoras es uno de los más conocidos y ampliamente utilizados en geometría Euclídea para resolver triángulos rectángulos e incluso figuras más complejas separándolas en triángulos rectángulos fáciles de calcular.

A lo largo de este post, vamos a explorar qué es el teorema de Pitágoras, las fórmulas del triángulo rectángulo y las aplicaciones del teorema de Pitágoras, todo esto acompañado de ejemplos y ejercicios resueltos para que valides estos nuevos conocimientos.
Teorema de Pitágoras
Es una fórmula, proveniente de la Geometría Euclidiana denominada así en honor al matemático griego Pitágoras, que establece una relación entre los 3 lados de un triángulo rectángulo. Es decir, conocidos dos de ellos es posible calcular el otro con esta ecuación.
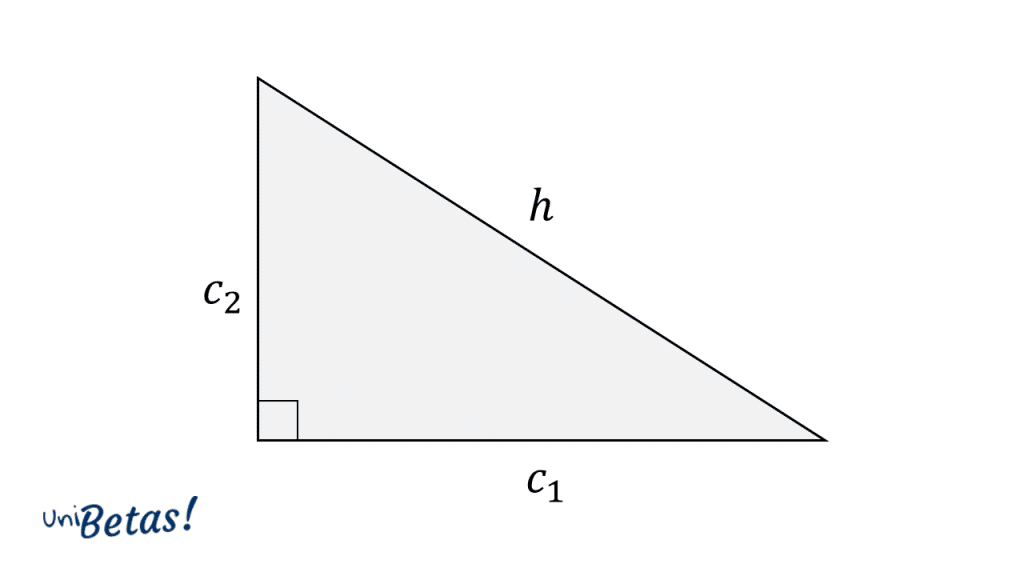
La definición formal del Teorema de Pitágoras establece que:
Escrito en lenguaje algebraico, esta relación quedaría como:
{h}^{2}={{c}^{2}}_{1}+{{c}^{2}}_{2}
Donde {C}_{1} y {C}_{2} son los catetos del triángulo rectángulo. Otra forma de interpretar al Teorema de Pitágoras, es a través de las áreas que forman los cuadrados representados por cada uno de los lados del triángulo rectángulo.
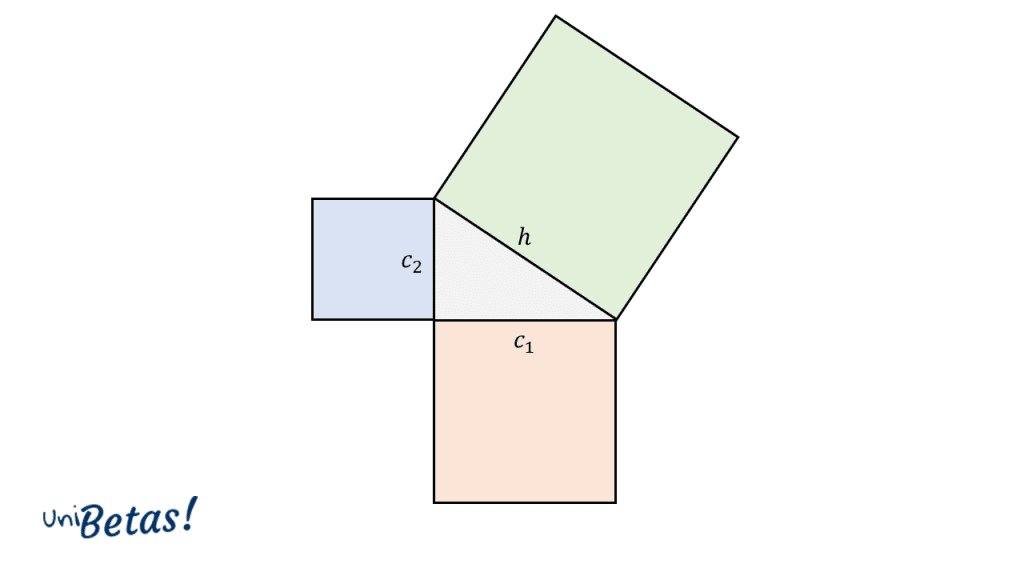
Si a cada uno de los lados del triángulo rectángulo lo asociamos con el lado de un cuadrado, la ecuación del Teorema de Pitágoras nos diría que: el área del cuadrado de lado h es igual a la suma de las áreas de los cuadrados de lado {C}_{1} y {C}_{2} .
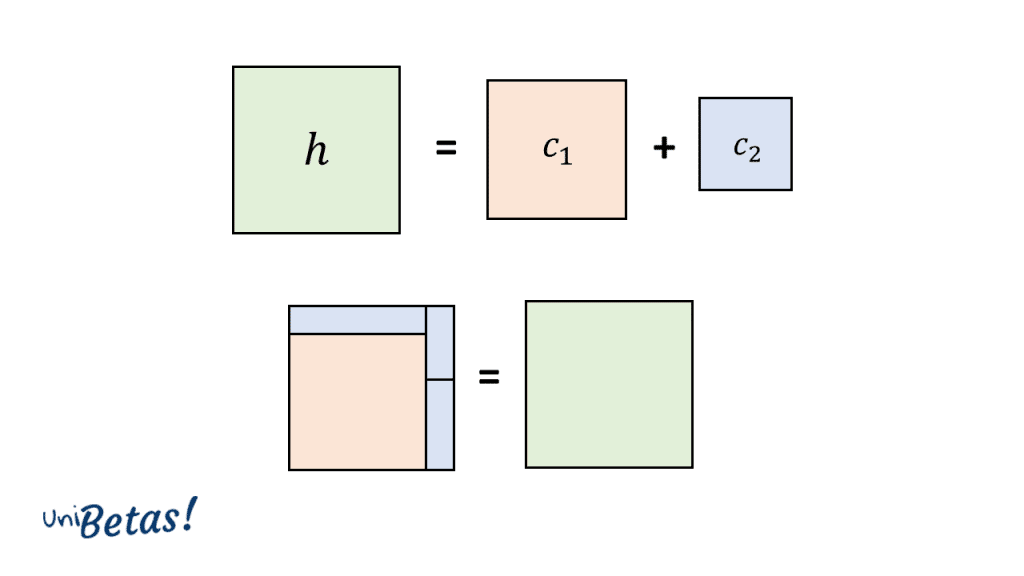
Demostración del teorema de Pitágoras
Existen numerosas vías para demostrar al teorema de Pitágoras, algunas mas gráficas otras recurren al álgebra, en este caso desarrollaremos una alternativa intermedia que puede realizarse con fórmulas y de manera gráfica. Cada paso lo ilustraremos con imágenes para facilitar la demostración.
Supongamos que tenemos un triángulo rectángulo cualquiera con lados hxy , donde h es la hipotenusa y tanto x como y son catetos.
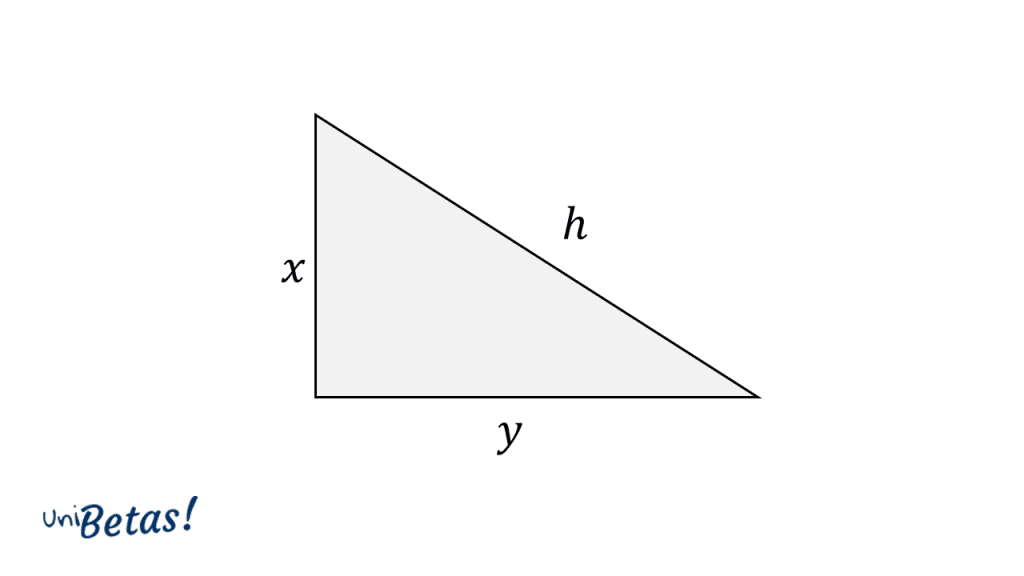
Comencemos por trazar los lados que faltan para formar un cuadrado de lado h que encierre al triangulo rectángulo.
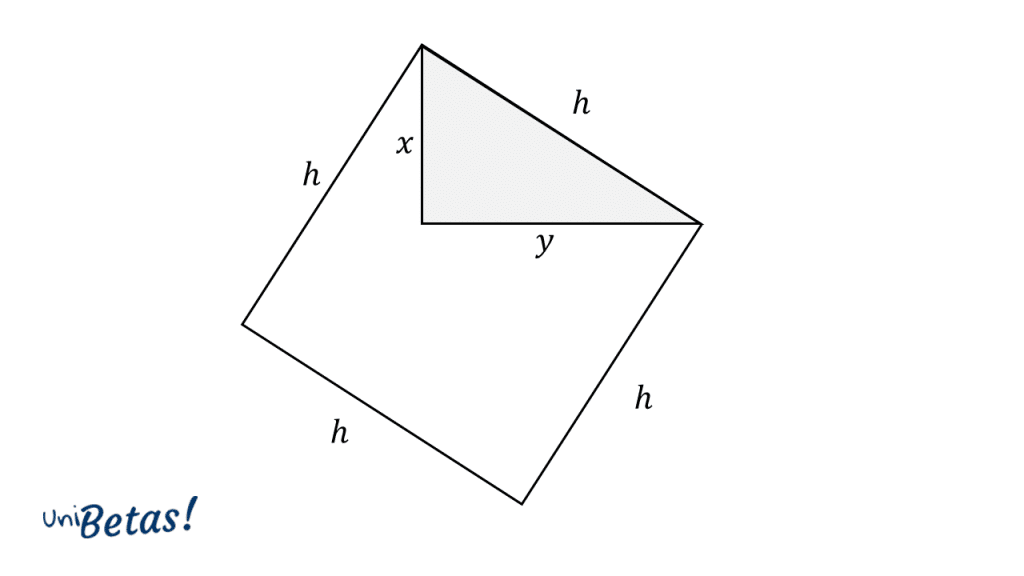
Ahora, vamos a encerrar al cuadrado con otro cuadrado, de tal forma que los vértices del cuadrado de lado h toquen a los lados del nuevo cuadrado. Examinando la figura, vemos como se repite el triángulo inicial hxy en la periferia, apareciendo también las distancias x y y en los lados del nuevo cuadrado.
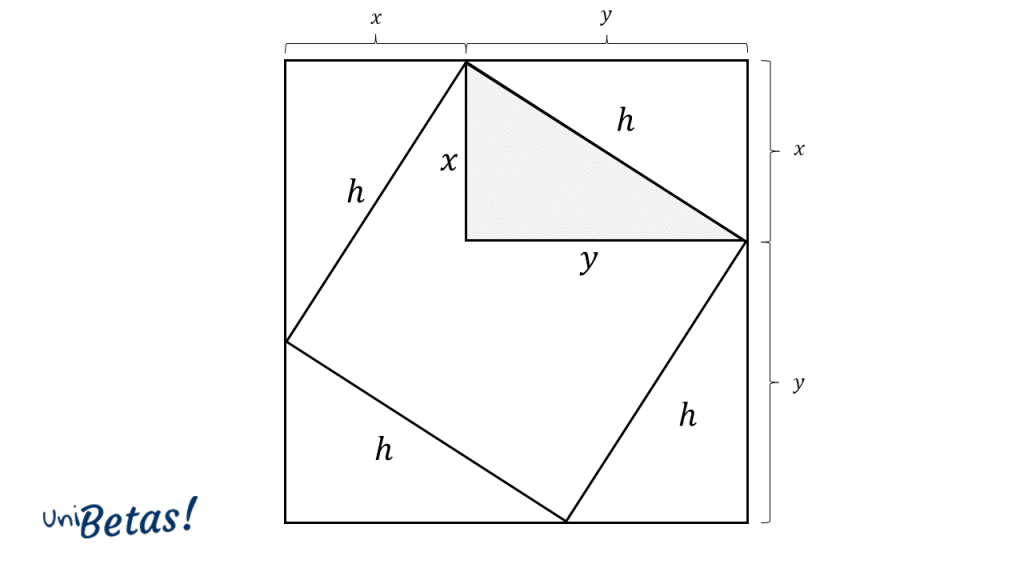
Podemos escribir el área del cuadrado de lado x+y como la suma del área de los triángulos hxy de la periferia mas el área del cuadrado interior de lado h .
{\left(x+y\right)}^{2}=4 \frac{x\bullet y}{2}+{h}^{2}
Desarrollamos.
{x}^{2}+2xy+{y}^{2}=2xy+{h}^{2}
Simplificamos el término 2xy de ambos lados.
{x}^{2}+{y}^{2}={h}^{2}
Obtenemos finalmente la fórmula del teorema de Pitágoras.
Otra forma de demostrar al teorema de Pitágoras, muy similar a la que hemos recurrido en este caso, hace uso de las áreas de los cuadrados y triángulos que se forman, pero desplazándolas de otra manera.
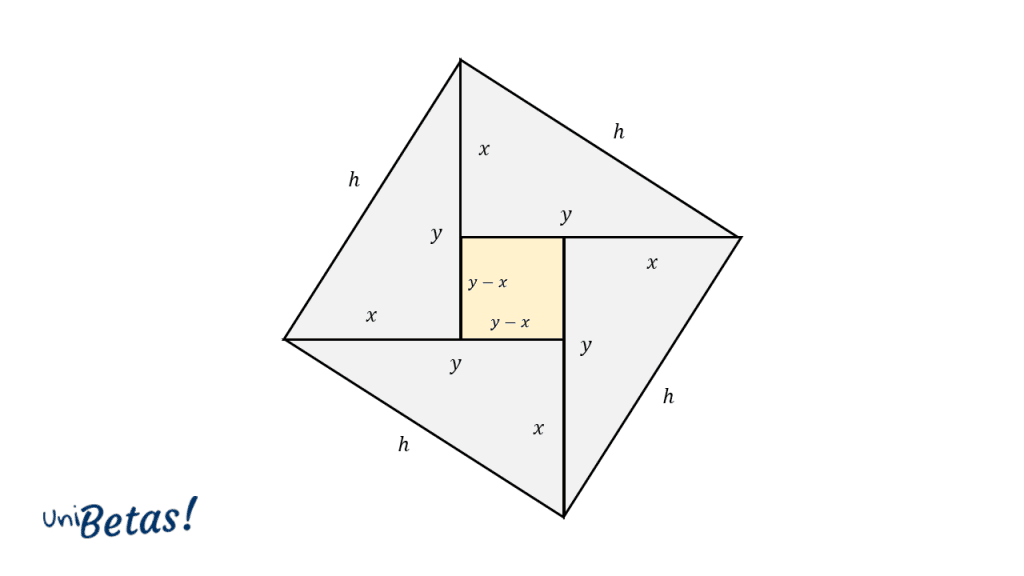
En este caso, vamos como se forma nuevamente el cuadrado de lado h y, dentro de él coexisten 4 triángulos xyh y un cuadrado en el centro de lado y-x . Por tanto, podemos escribir el área del cuadrado de lado h como:
{h}^{2}=4\frac{x\bullet x}{2}+{\left(y-x\right)}^{2}
Desarrollamos y simplificamos la expresión.
{h}^{2}=2xy+{y}^{2}-2xy+{x}^{2}={y}^{2}+{x}^{2}
Obtenemos, nuevamente, al teorema de Pitágoras.
{h}^{2}={y}^{2}+{x}^{2}
Teorema de Pitágoras fórmula
La fórmula del teorema de Pitágoras permite determinar un lado desconocido teniendo como dato a los otros dos. A continuación, te presento las variantes del teorema de Pitágoras, con las que podrás determinas cualquiera de los lados de un triángulo rectángulo:
Calcular el lado {C}_{1}
{c}_{1}=\sqrt{{h}^{2}-{{c}^{2}}_{2}}
Calcular el lado {C}_{2}
{c}_{2}=\sqrt{{h}^{2}-{{c}^{2}}_{1}}
Calcular a la hipotenusa
h=\sqrt{{{c}^{2}}_{1}+{{c}^{2}}_{2}}
A continuación, te dejo tres ejemplos de aplicación del teorema de Pitágoras con las tres fórmulas anteriores. Ten en cuenta que la ecuación que permite calcular a {c}_{1} o a {c}_{2} es la misma, solo debes considerar que a la izquierda va el lado desconocido y dentro del radical el lado conocido junto a la hipotenusa.
Este conjunto de fórmulas de Pitágoras se conoce como los 3 corolarios del teorema de Pitágoras.
El par de demostraciones que hemos adjuntado en este post son apenas una mínima fracción de las existentes incluso.
Ejemplo 1: cálculo de la hipotenusa de un triángulo rectángulo
Dado el triangulo rectángulo de la figura, calcule la longitud de su hipotenusa aplicando el teorema de Pitágoras.
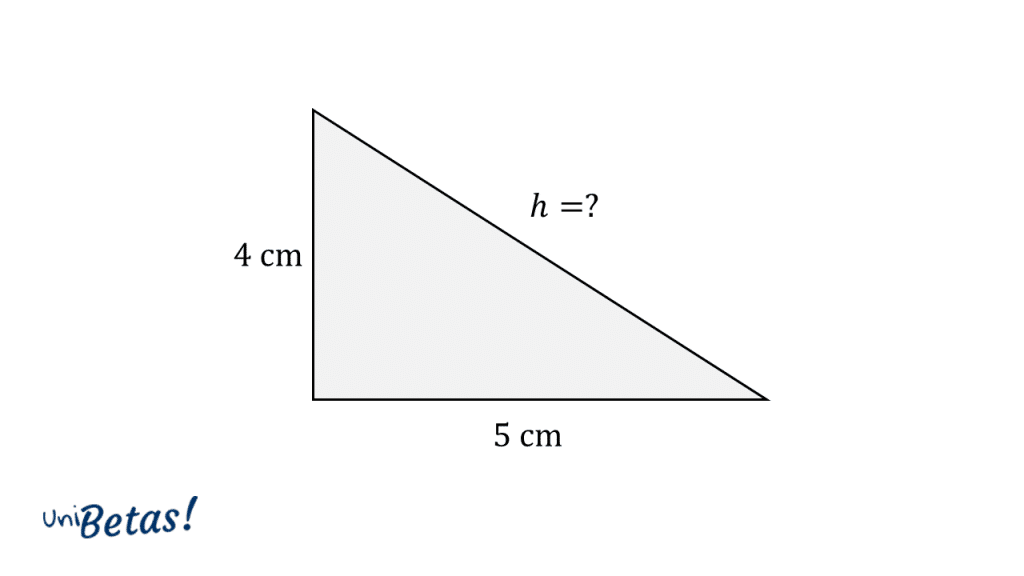
Solución:
Comenzamos por identificar los lados del triángulo. El primer cateto será {c}_{1}=4 , el segundo {c}_{2}=5 y la hipotenusa h , la cual es desconocida. Sustituimos los valores en la fórmula para sacar la hipotenusa:
{h}^{2}={c}_{1}^{2}+{c}_{2}^{2}
Sustituyendo.
{h}^{2}={4}^{2}+{5}^{2}
Calculamos los cuadrados de 4 y 5.
{h}^{2}=16+25=41
Ahora, aplicamos raíz cuadrada en ambos miembros para despejar la hipotenusa.
h=\sqrt{41}
Podemos concluir este ejemplo aportando dos observaciones. Primero, que no importa el orden que se le dé a los catetos en la ecuación, el resultado será el mismo. Si en lugar de {c}_{1}=4 y {c}_{2}=5 hubiésemos escrito {c}_{1}=5 y {c}_{2}=4 , se obtiene que:
h=\sqrt{{5}^{2}+{4}^{2}}=\sqrt{41}
Por otro lado, si aprendiste bien sobre el despeje de radicales con índice 2, sabrás que hay dos soluciones: una positiva y otra negativa ¿por qué no escogimos la negativa en lugar de la positiva? Porque en este caso estamos tratando con distancias y estas siempre son positivas.
Ejemplo 2: calcular catetos conociendo la hipotenusa
Determine la longitud del cateto desconocido aplicando la fórmula correcta del teorema de Pitágoras.
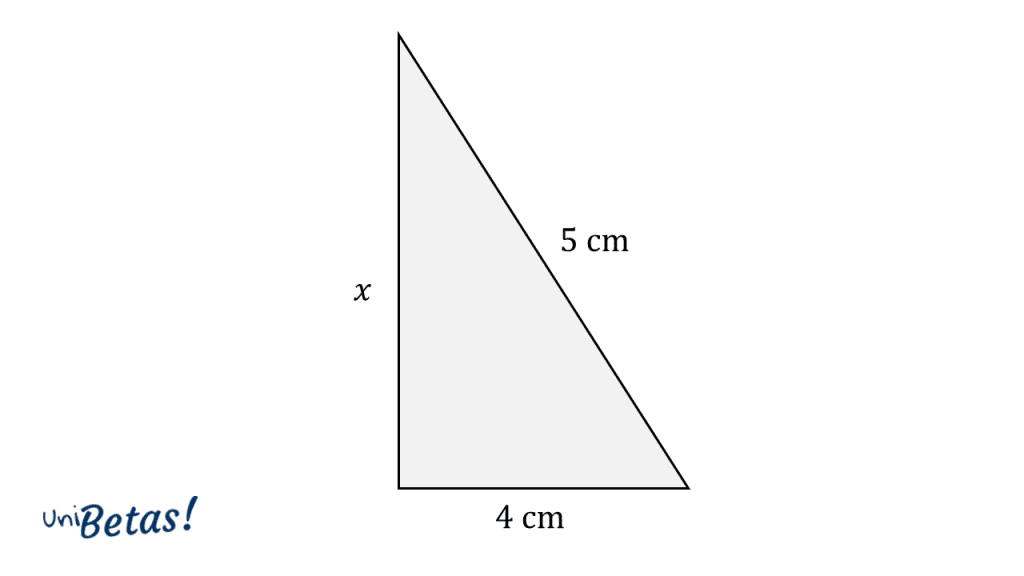
Solución:
Teniendo en cuenta la conclusión dada en el ejemplo anterior, sabemos que podemos calcular la longitud del cateto desconocido aplicando la siguiente ecuación:
x=\sqrt{{5}^{2}-{4}^{2}}=\sqrt{25-16}
x=\sqrt{9}=3
El cateto restante tiene una longitud de 3 centímetros.
Consideraciones del Teorema de Pitágoras
Recapitulando todo lo mencionado hasta el momento, es necesario aclarar algunas dudas que pueden surgir al utilizar la ecuación de Pitágoras.
- No puede utilizarse para triángulos que no sean rectángulos. Pero si es posible trazar segmentos dentro de un triángulo irregular para formar en su interior triángulos rectángulos
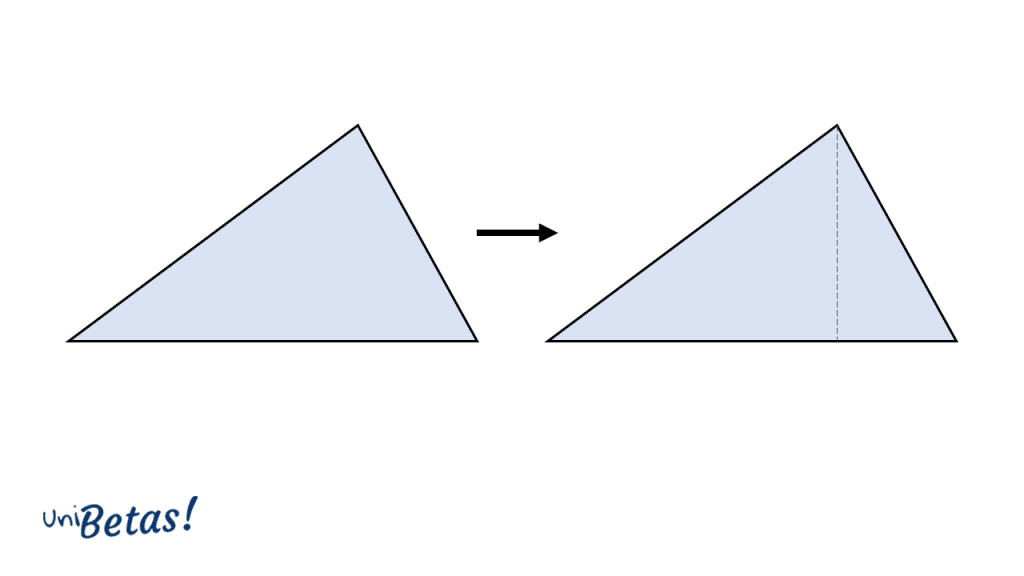
- Como sabes, al despejar una raíz cuadrada el resultado puede ser positivo o negativo. Siempre se toma el resultado positivo porque los lados y las longitudes son siempre positivas
- Los catetos {C}_{1} y {C}_{2} no tienen una distinción particular en la ecuación. Cualquier lado que no sea la hipotenusa puede llamarse {C}_{1} e inmediatamente el otro será el cateto {C}_{2}
- En problemas de decidir el camino más corto donde entran en juego triángulos rectángulos, la distancia de la hipotenusa es menor la suma de las longitudes de los catetos h<{c}_{1}+{c}_{2} , por tanto, el camino más corto es la hipotenusa
El Triángulo Rectángulo
Con todo lo comentado hasta ahora, vale la pena hacer un pequeño inciso para recordar que es un triángulo rectángulo y definir cada una de sus partes.
Los lados que forman el ángulo de 90° se denominan catetos, mientras que el lado en diagonal que une los extremos distantes de los catetos se llama hipotenusa. Como se ha mencionado a lo largo del post, el triángulo rectángulo cumple con el Teorema de Pitágoras y son el mismo tipo de triángulo que hemos estado estudiando.
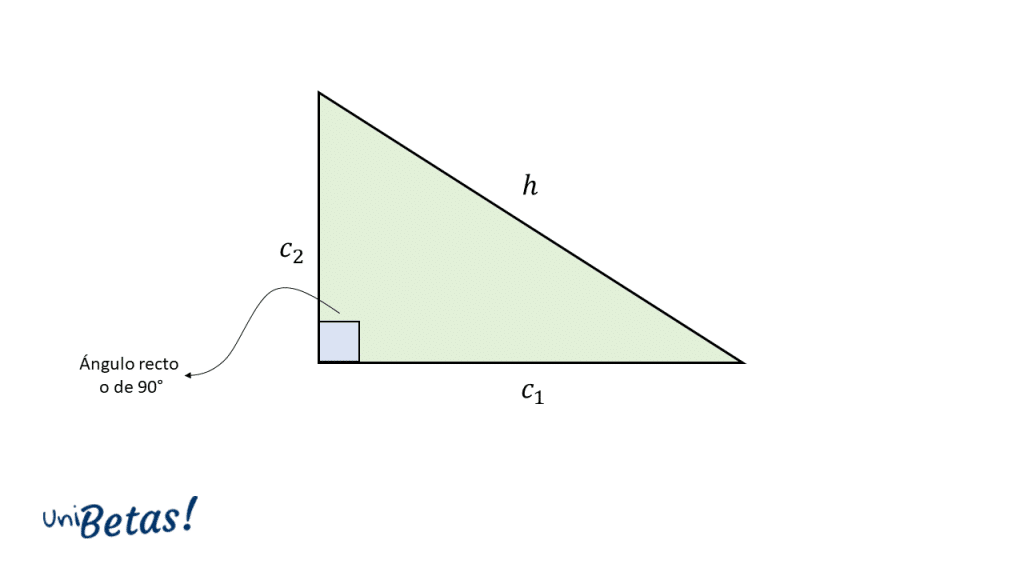
Con la explicacion anterior, hemos definido indirectamente qué es un cateto y que es una hipotenusa. Podemos resumir esto de la siguiente manera:
- Cateto: lado que, junto a otro, forman el ángulo recto de un triangulo rectángulo
- Hipotenusa: es el lado más largo en un triangulo rectangulo. La hipotenusa tambien puede identificarse como el lado opuesto al ángulo recto del triangulo rectángulo
Propiedades de los triángulos rectángulos
A continuación, enumeramos las propiedades mas resaltantes de los triángulos rectángulos, empleadas con frecuencia al resolver problemas de geometría.
- Posee dos ángulos agudos los cuales suman 90°
- Cuando los catetos tienen la misma longitud, el triángulo se denomina isorectángulo o triangulo rectángulo isósceles
- Para calcular el área, es indistinto seleccionar uno como base y otro como altura
Aplicaciones del Teorema de Pitágoras
Siempre que en un problema se presente un triángulo rectángulo o la necesidad de medir la distancia euclídea más corta entre dos puntos, el Teorema de Pitágoras estará allí para ayudarnos. Algunas de las aplicaciones más comunes son:
- Calcular alguno de los lados de un triángulo rectángulo.
- Determinar si un triángulo es o no rectángulo. Para ello debe cumplirse que:
{h}^{2}={{c}^{2}}_{1}+{{c}^{2}}_{2}
- Para calcular el módulo de un vector en dos y tres dimensiones.
‖V‖=\sqrt{{{v}^{2}}_{x}+{{v}^{2}}_{y}} con V\in {R}^{2}
‖V‖=\sqrt{{{v}^{2}}_{x}+{{v}^{2}}_{y}+{{v}^{2}}_{z}} con V\in {R}^{3}
- Para medir la distancia entre dos puntos en el plano o el espacio tridimensional.
d\left(x,y\right)=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}}
d\left(x,y,z\right)=\sqrt{{\left({x}_{2}-{x}_{1}\right)}^{2}+{\left({y}_{2}-{y}_{1}\right)}^{2}+{\left({z}_{2}-{z}_{1}\right)}^{2}}
- Los triángulos rectángulos son la base para la descripción de las identidades trigonométricas en la circunferencia unitaria. Se llama unitaria porque tiene radio igual a 1.
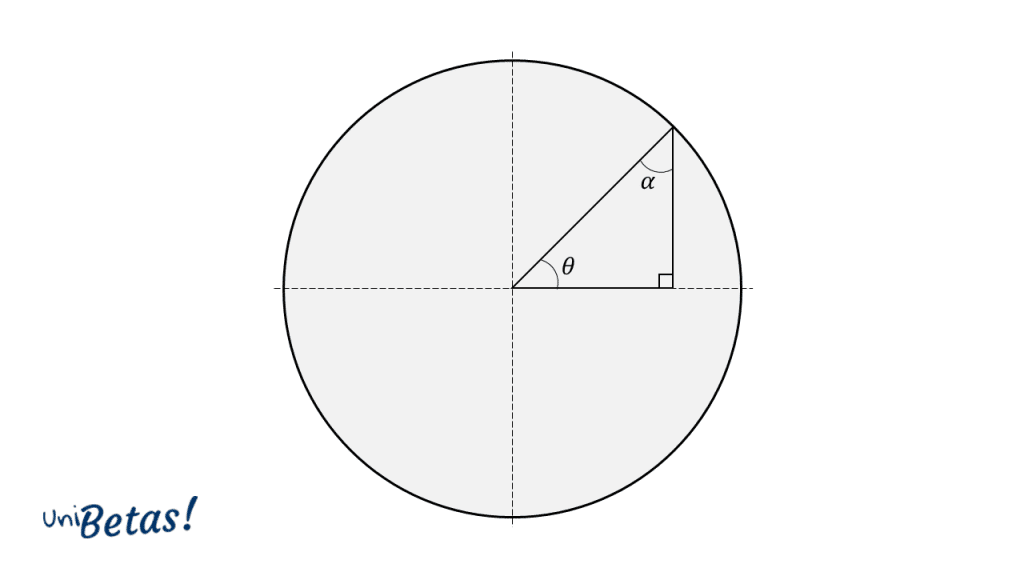
Si tomamos en cuenta el ángulo \theta , nos queda la siguiente descomposición en base al teorema de Pitágoras:
1={\mathrm{sin}}^{2}\theta +{\mathrm{cos}}^{2}\theta
Esta identidad recibe el nombre de identidad Pitagórica.
- En el modelado matemático de problemas físicos y de análisis matemático. Algunas de estas aplicaciones son:
- La altura de una escalera, la sombra de un árbol o un edificio. En general, para problemas en los que es necesario calcular proyecciones.
- Para medir las proyecciones de una fuerza sobre el eje que produce trabajo (teorema del trabajo y la energía). Esto aplica para descomponer cualquier magnitud física de tipo vectorial.
- Al descomponer alguna de las leyes de Newton del movimiento en las componentes de los ejes coordenados.
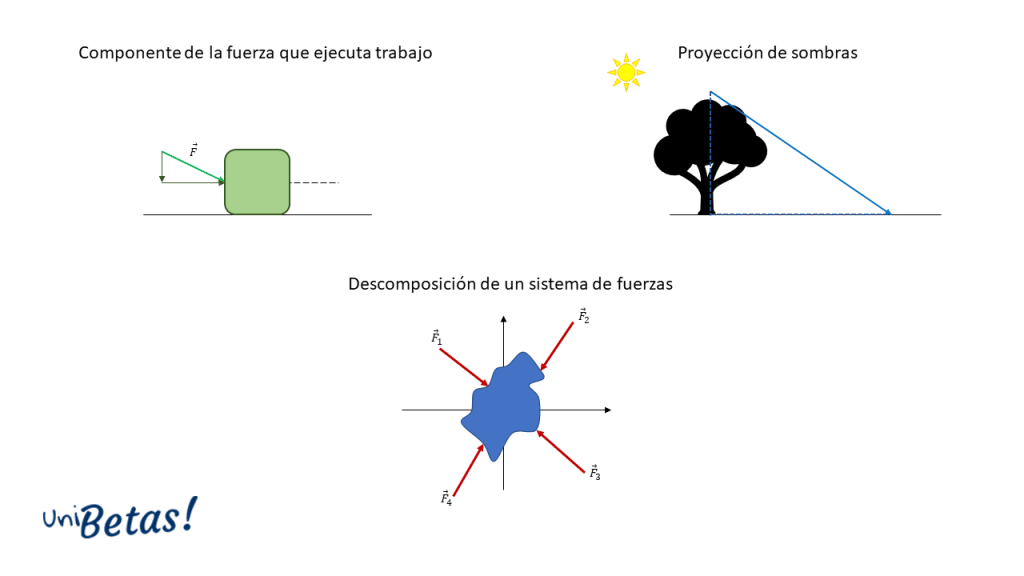
- En geometría plana, para subdividir polígonos regulares como rombos o pentágonos, al momento de analizar propiedades como área, apotema y perímetro.
- En problemas de optimización, la mayoría de las soluciones converge en encontrar triángulos rectángulos para modelar el problema planteado.
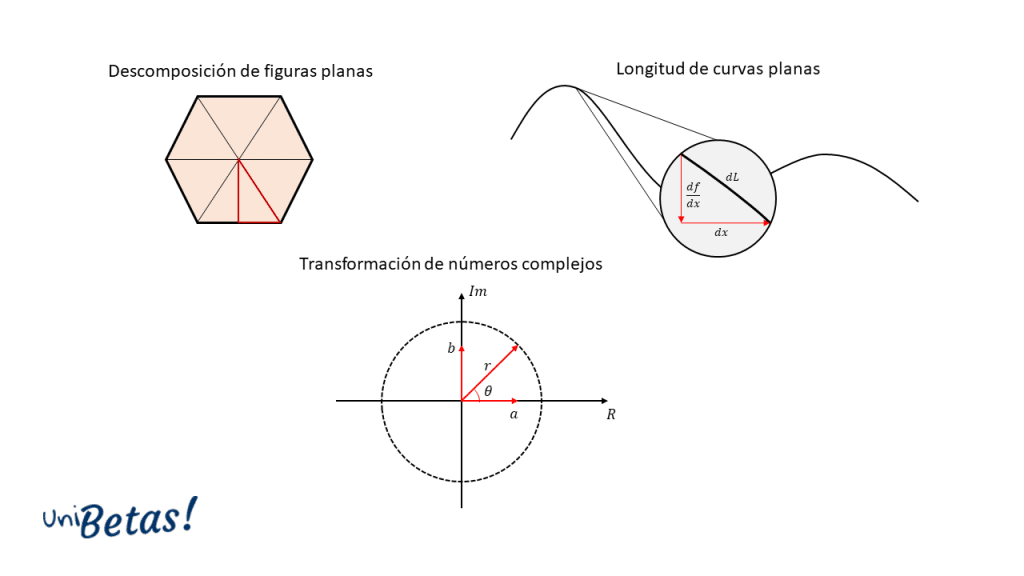
- En cálculo integral, el teorema de Pitágoras es fundamental para el método de integración por sustitución trigonométrica, se emplea para medir la longitud de curvas aplicando una descomposición diferencial de la misma en forma de triangulo rectángulo.
- En geometría analítica, el teorema de Pitágoras es fundamental para descomponer vectores y para describir a las secciones cónicas como la circunferencia, parábola, elipse y la hipérbola.
- En números complejos, para transformar de la forma binomial a+ib a la forma exponencial r{e}^{i\theta } , el módulo del fasor r se calcula aplicando la fórmula del teorema de Pitágoras.
Y estas siguen siendo solo un subconjunto muy pequeño de todas las aplicaciones que posee el teorema de Pitágoras, podríamos entender el montón de demostraciones, como una forma natural del teorema para manifestarse en todas las ramas de las ciencias; no solo en matemáticas y en física.
¿Para qué sirve el Teorema de Pitágoras?
A partir de las secciones anteriores, sabemos que el teorema de Pitágoras permite hallar la longitud de cualquiera de los tres lados de un triángulo rectángulo cuando conocemos dos de ellos, pero en la vida real ¿dónde entra en juego la fórmula de Pitágoras?
Ya que relaciona distancias entre sí, es una fórmula útil a la hora de construir casi cualquier cosa. Los arquitectos e ingenieros de la antigüedad emplearon el Teorema de Pitágoras (muchas veces sin saber que lo que era) para construir puentes, muros y escaleras perfectamente alineados y perpendiculares.
En carpintería, fabricación de piezas mecánicas y estructuras, es una herramienta fundamental para unir por sus extremos piezas para que queden perfectamente perpendiculares entre ellas.
Para la creación de videojuegos 2D y 3D, el Teorema de Pitágoras y la geometría (analítica y elemental) permiten medir distancias entre sólidos para el cálculo de colisiones, velocidades, aceleraciones y trayectorias. Sin ir más lejos, todos los motores gráficos de cualquier aplicación informática implementan el teorema de Pitágoras para la localización de los elementos en ella.
Los sistemas de posicionamiento global, conducción autónoma y CNC (Control Numérico Computarizado), utilizan polígonos y técnicas de triangulación basadas en el teorema de Pitágoras para delimitar zonas, establecer rutas y medir distancias.
Historia del Teorema de Pitágoras
Aunque se estima que el matemático y filósofo griego Pitágoras junto a su importante teorema datan del siglo V a.C. existen documentos históricos provenientes del siglo XX a.C. (más de mil años antes del nacimiento de Pitágoras), sobre tablillas babilónicas con ternas pitagóricas: grupos de 3 números enteros que cumplen el teorema de Pitágoras.

La presencia de las ternas pitagóricas prevalece a lo largo de la antigüedad, debido a que permitió a los arquitectos de la época construir ángulos rectos perfectos a través de distancias y sin la medición de ángulos, actividad que no se podía realizar con tanta precisión.
Documentos de la China e India antigua, muestran como sus matemáticos buscaban fervientemente dichas ternas, ya que eran importantes para el desarrollo de sus infraestructuras y el comercio, que daban forma al poderío de estas civilizaciones ante el resto del mundo.
Los griegos fueron capaces de marcar la diferencia gracias al enfoque que les daban a las matemáticas. Entendieron que los resultados demostrables y universales permitían construir nuevas matemáticas, de allí la notación algebraica del teorema, salto que evocó en la primera conjunción entre el álgebra y la geometría.
Quizá una de las primeras grandes revoluciones que causó el teorema de Pitágoras, además de su utilidad geométrica, fue el descubrimiento de los números irracionales: cantidades que poseen infinitos decimales y no pueden ser expresadas como una fracción.
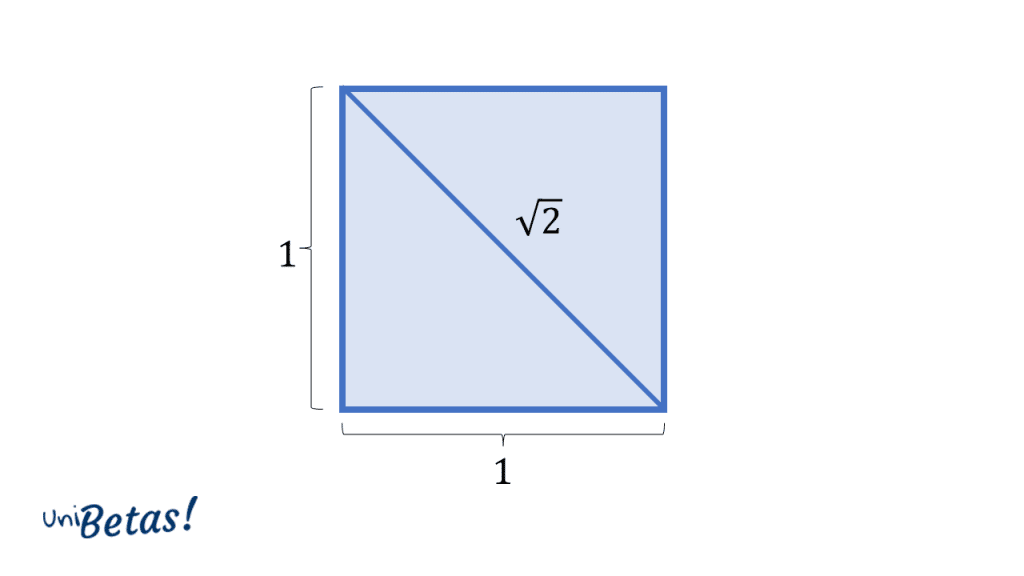
En la actualidad, el teorema de Pitágoras sigue siendo una herramienta indispensable y marca el punto de partida en muchos debates matemáticos de alto nivel en ramas sofisticadas como: topología, geometría algebraica (mezcla entre algebra abstracta y geometría analítica), teoría de números, teoría de la medida, calculo infinitesimal y muchas más.
Las ternas Pitagóricas
Se denomina terna pitagórica o terna de Pitágoras a tres números enteros que cumplen con el teorema de Pitágoras. Los números de dichas ternas son, naturalmente, positivos y distintos de cero. La forma de referirnos a las ternas pitagóricas es mediante la notación \left(a, b, c\right) , donde a y b son los catetos y c es la hipotenusa.
Otra acotación que se puede hacer sobre las ternas pitagóricas, es que las mismas convierten a la fórmula de Pitágoras {c}^{2}={a}^{2}+{b}^{2} en una ecuación diofántica, es decir, una ecuación con 3 incógnitas de la que se buscan únicamente soluciones enteras para sus variables.
El mismo Pitágoras desarrolló una parametrización de a , b y c , de tal forma que los tres números dependan de un mismo parámetro t . De esta forma, es posible encontrar cualquier terna Pitagórica sustituyendo en las ecuaciones cualquier valor entero de t mayor que 1.
\left\{\begin{array}{c}a={t}^{2}-1\\ b=2t\\ c={t}^{2}+1\end{array}\right.
\forall t\in \mathrm{N}\mathrm{ }\wedge \mathrm{t}>1
Las ternas Pitagóricas tienen la propiedad de que pueden generar otras ternas proporcionales en un factor \alpha \in \mathrm{N} a los valores de la terna original, es decir:
\left({a}_{2},{b}_{2},{c}_{2}\right)=\alpha \left({a}_{1},{b}_{1},{c}_{1}\right)
Si tomamos a la mínima terna pitagórica \left(3, 4, 5\right) y multiplicamos sus valores por 2, obtenemos que:
\left({a}_{2},{b}_{2},{c}_{2}\right)=\left(9, 8, 10\right)
Sustituyendo en la fórmula de Pitágoras:
{10}^{2}={9}^{2}+{8}^{2}\to 100=100
\left(9, 8, 10\right) es una terna pitagórica.
Teorema de Pitágoras: Comprobación de triángulos
El teorema de Pitágoras no solo es útil para comprobar triángulos rectángulos, de hecho, es una fácil y rápida de comprobar cualquier triangulo si es que no se tiene una representación gráfica del mismo.
Partimos de la fórmula original.
{c}^{2}={a}^{2}+{b}^{2}
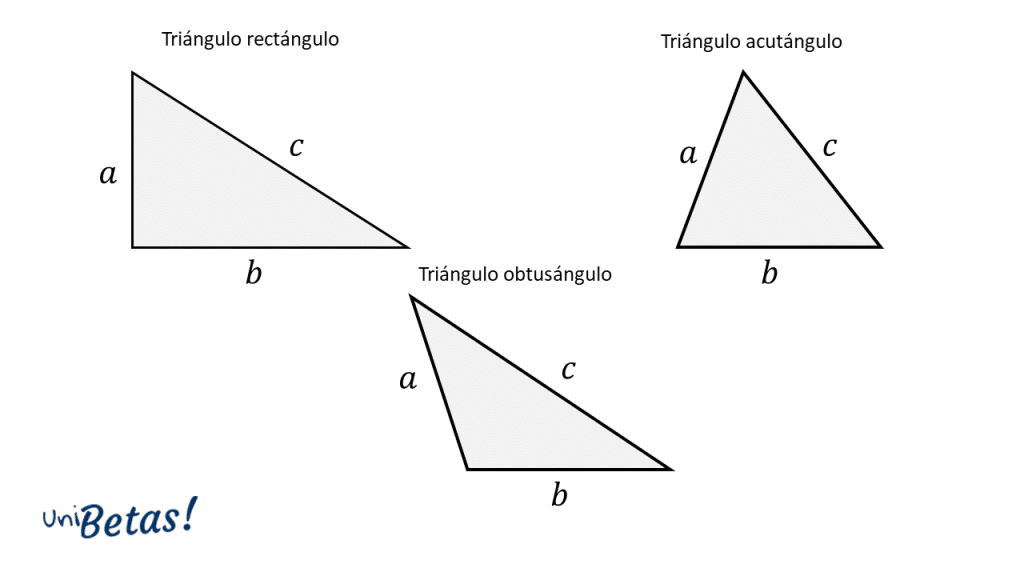
Este es el caso de un triángulo rectángulo.
Si resulta que al sustituir los valores se obtiene que:
{c}^{2}>{a}^{2}+{b}^{2}
El triángulo en cuestión es obtusángulo, es decir, con un ángulo interno mayor a 90°.
Por el contrario, si se verifica que:
{c}^{2}<{a}^{2}+{b}^{2}
Entonces el triángulo es acutángulo, es decir, todos sus ángulos internos son menores a 90°.
Ejercicios sobre el Teorema de Pitágoras
Los siguientes ejercicios resueltos pretenden exponer el potencial que tiene el teorema de Pitágoras a la hora de resolver todo tipo de problemas. No entraremos en temas de cálculo y física porque no es la intención del post, pero si exploraremos varios problemas geométricos.
Ejercicio 1
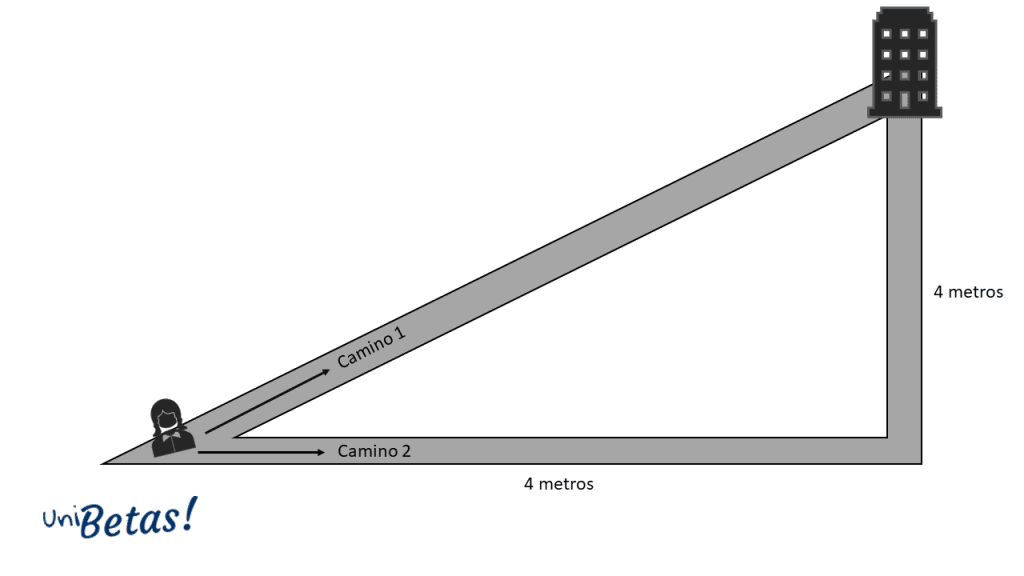
María debe llegar pronto a su clase de matemáticas y para ello tiene en frente dos caminos que puede seguir para llegar al aula, ¿cuál camino debe elegir si pretende transitar por el más corto?
Solución:
La longitud del camino 2 la podemos determinar con la suma de la trayectoria horizontal y la trayectoria vertical, es decir:
\mathrm{c}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{o}\mathrm{ }1=4+4=8\mathrm{ }\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}
Ahora, la distancia del camino 1 la podemos calcular aplicando el teorema de Pitágoras. En este caso, el camino 2 sería la hipotenusa y las longitudes horizontal y vertical del camino 2 corresponden a los catetos del triángulo rectángulo.
\mathrm{c}\mathrm{a}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{o}\mathrm{ }2=\sqrt{{4}^{2}+{4}^{2}}=\sqrt{32}
Si calculamos el valor exacto de la raíz cuadrada de 32 obtenemos que es aproximadamente igual a 5.6568, menor que los 8 metros que mide el camino 2, de hecho, esta es una de las propiedades antes enunciadas del teorema de Pitágoras.
Concluimos entonces que María debe tomar el camino 1 para llegar antes a su clase.
Ejercicio 2
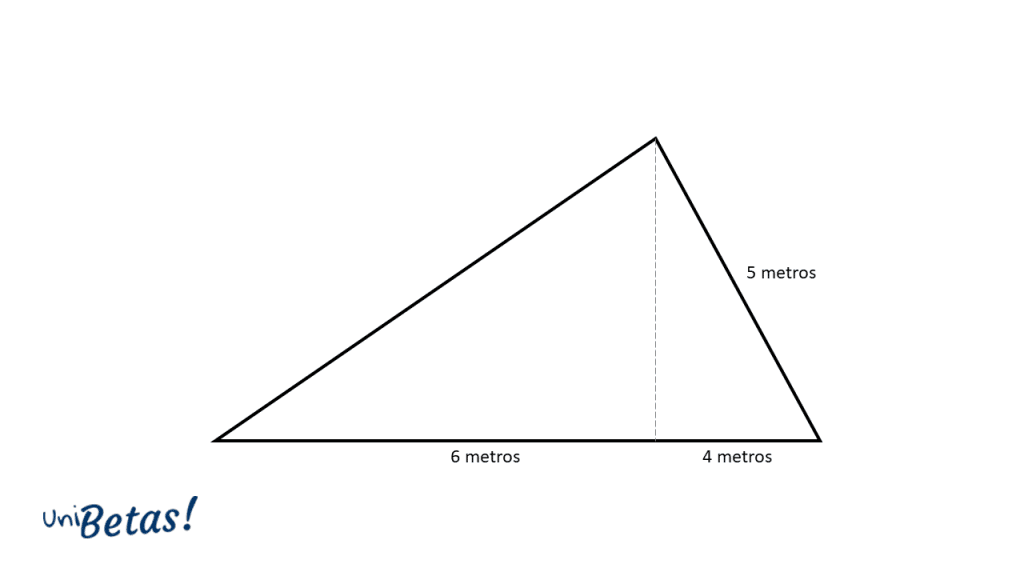
Dado el siguiente triángulo, determina su área y perímetro.
Solución:
Para calcular el área del triángulo, debemos aplicar la conocida formula de base por altura entre dos:
{A}_{t}=\frac{bh}{2}
La altura puede calcularse fácilmente aplicando el teorema de Pitágoras en el pequeño triangulo rectángulo de la derecha. Aplicamos la fórmula del cateto.
c=\sqrt{{5}^{2}-{4}^{2}}=3
Por otra parte, la base del triángulo grande mide 6+4=10 \mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s} . Sustituimos y calculamos.
{A}_{t}=\frac{10*3}{2}=15 {\mathrm{m}}^{2}
Para calcular el perímetro, necesitamos la longitud desconocida en el triángulo, si examinamos detenidamente la parte izquierda del mismo, encontramos que se forma otro triangulo rectángulo 6/3/x. El lado desconocido x corresponde con la hipotenusa de dicho triangulo.
x=\sqrt{{6}^{2}+{3}^{2}}=\sqrt{45}=3\sqrt{5}
El perímetro se calcula como la suma de todas las aristas:
P=3\sqrt{5}+10+5=3\sqrt{5}+15
Calculando el valor aproximado del radical.
P=21.7 \mathrm{m}
Ejercicio 3
Se desea medir la altura de un árbol. A determinada hora del día, se sabe que la sombra del mismo en el suelo mide 2.5 metros. Por otra parte, la longitud que separa la punta del árbol y el extremo de la sombra en el suelo mide 4 metros. Con estos datos, calcule la altura del árbol.
Solución:
En este caso, debemos identificar que lados del triángulo rectángulo formado por la sombre, el árbol y la distancia que une sus puntas tenemos. Desde ahora, nos permitimos asumir que el árbol es perfectamente recto si no, el triángulo ya no sería rectángulo.
La distancia entre las puntas del árbol y la sombra sería la hipotenusa y la longitud de la sombra seria uno de los catetos. Por tanto, la altura del árbol es el cateto restante.
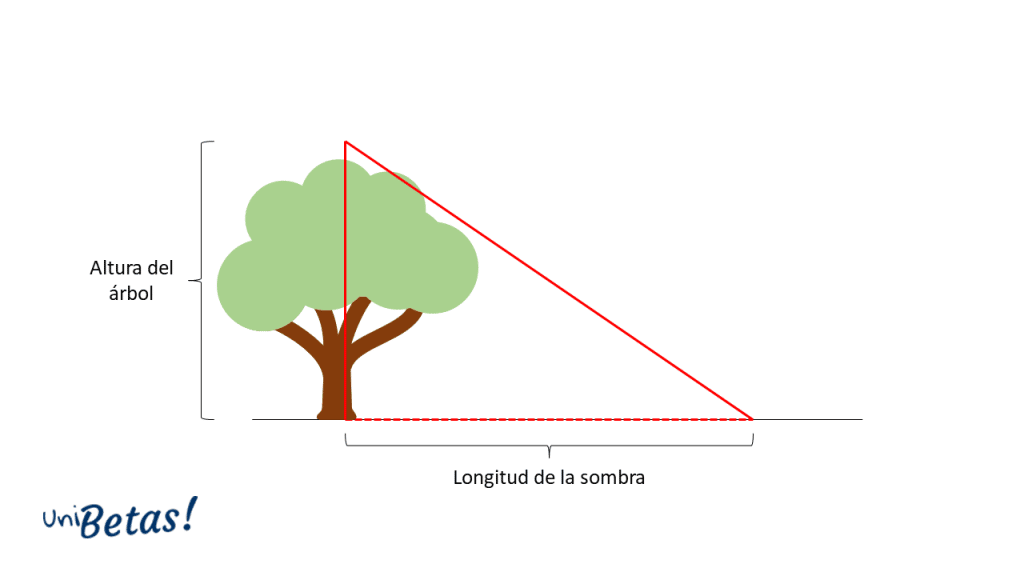
Con este gráfico, queda claro que debemos aplicar la fórmula del teorema de Pitágoras para el cálculo del cateto.
{c}_{2}=\sqrt{{h}^{2}-{c}_{1}^{2}}
Sustituimos.
{c}_{2}=\sqrt{{4}^{2}-{2.5}^{2}}=3.12 \mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}
El árbol tiene una altura de 3.12 metros.
Ejercicio 4
Se tiene un triángulo rectángulo cuyos catetos miden 4 y 3 metros. Si a cada uno de los catetos se le duplica, ¿en qué proporción incrementa la hipotenusa?
Solución:
Este tipo de problema es bastante común en física y otras ciencias aplicadas, debido a que muchos fenómenos que dependen de la distancia a la que se encuentra la fuente se modelan a partir de vectores que, eventualmente, se miden aplicando el teorema de Pitágoras.
En esta línea de ideas, muchas veces interesa conocer en qué medida disminuye la intensidad de, por ejemplo, la intensidad de la fuerza eléctrica que experimenta una partícula cargada cuando se aleja cierta proporción de otra. Dicho problema se reduce en el que expone el enunciado.
Comencemos por calcular le hipotenusa del triángulo inicial.
{h}_{1}=\sqrt{{4}^{2}+{3}^{2}}=\sqrt{25}=5
Ahora, duplicamos la magnitud de los catetos.
{h}_{2}=\sqrt{{(2\bullet 4)}^{2}+{(2\bullet 3)}^{2}}=\sqrt{100}=10
Dividimos la hipotenusa 2 con la 3 para obtener la proporción de incremento.
\frac{{h}_{2}}{{h}_{1}}=\frac{10}{5}=2
Cuando los catetos duplican su tamaño, la hipotenusa también lo hace.
{h}_{2}=2{h}_{1}
Ejercicio 5
Para una obra civil, se necesita seleccionar escaleras que cumplan con las normas municipales, si no, la obra podría ser cancelada. Uno de los estatutos establece que para paredes que miden más de 1.5 metros, las patas de las escaleras deben tener una separación de 1/3 de la pared para garantizar estabilidad.
Si las pareces que se pretenden construir miden 2 metros, ¿cuál debe ser la altura de las escaleras que se deben comprar?
Solución:
Teniendo en cuenta que la altura de las paredes es 2 metros y que la separación de las patas respecto de la pared ha de ser \frac{2}{3}=0.66 \mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s} , podemos dibujar el siguiente triangulo rectángulo.
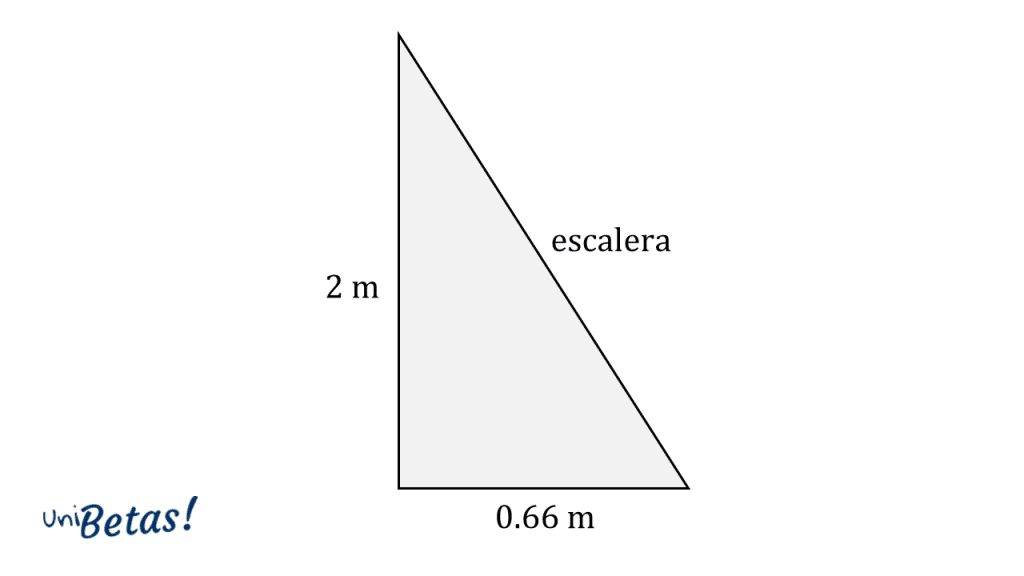
Sustituimos los respectivos valores en la fórmula de Pitágoras:
\mathrm{e}\mathrm{s}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}\mathrm{r}\mathrm{a}=\sqrt{{2}^{2}+{0.66}^{2}}=2.1 \mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}
La escalera que debe seleccionarse para la obra ha de medir 2.1 metros de largo.
Ejercicio 6
Calcule el área del siguiente polígono compuesto.
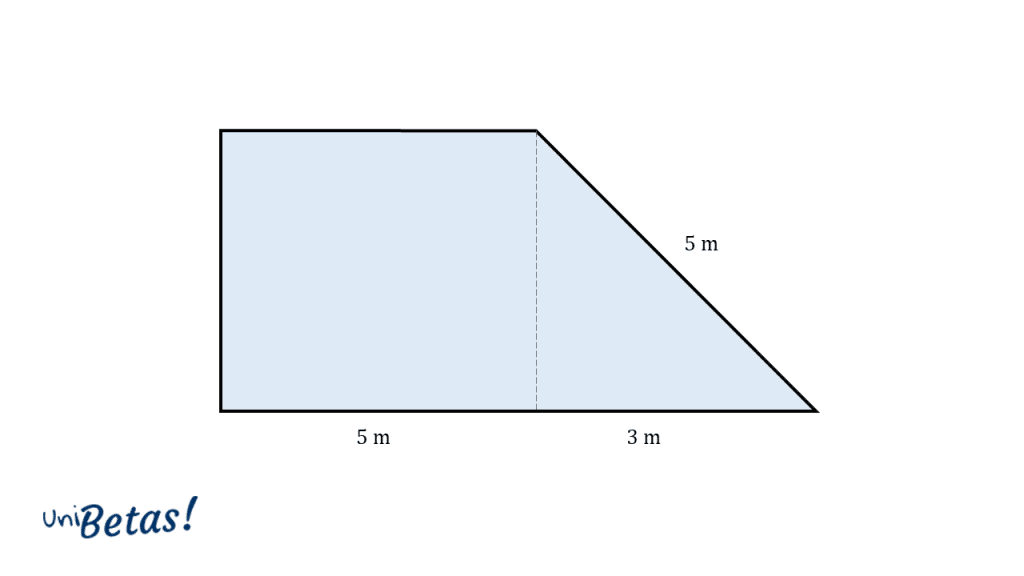
Solución:
Para calcular el área total de la figura, debemos separarla en dos: un rectángulo y un triángulo rectángulo. El área de la figura queda expresada como:
{A}_{f}={A}_{c}+{A}_{t}
El área del rectángulo se calcula como el producto de la base por la altura.
{A}_{c}={b}_{c}{h}_{c}
En este caso, solo tenemos la base y la altura es, por ahora, desconocida. Por otro lado, el área del triángulo rectángulo es base por altura entre 2.
{A}_{t}=\frac{{b}_{t}{h}_{t}}{2}
Examinando la figura, nos daremos cuenta que la altura del triangulo es igual a la altura del rectángulo y la misma se puede determinar aplicando uno de los corolarios del teorema de Pitágoras.
{h}_{t}={h}_{c}
{h}_{t}=\sqrt{{5}^{2}-{3}^{2}}=4
Sustituimos este resultado en las ecuaciones para obtener:
{A}_{f}=5*4+\frac{3*4}{2}=26 {\mathrm{m}}^{2}
El área de la figura es de 26 metros cuadrados.
Ejercicio 7
El sistema de navegación de un coche indica la proximidad o lejanía del punto de destino indicando dos valores en coordenadas cardinales: una representa este u oeste y la segunda norte o sur. En un momento dado, el coche le notifica al conductor 4 km al este y 3 km al norte, ¿cuál es la distancia rectilínea que separa al coche y al punto final de destino?
Solución:
En este caso, el teorema de Pitágoras lo ocupamos para determinar la longitud rectilínea entre el coche y el punto de destino. Es interesante resaltar, que la forma en la que el coche indica la posición es de tipo vectorial, por lo que esta es una de las aplicaciones especiales del teorema de Pitágoras.
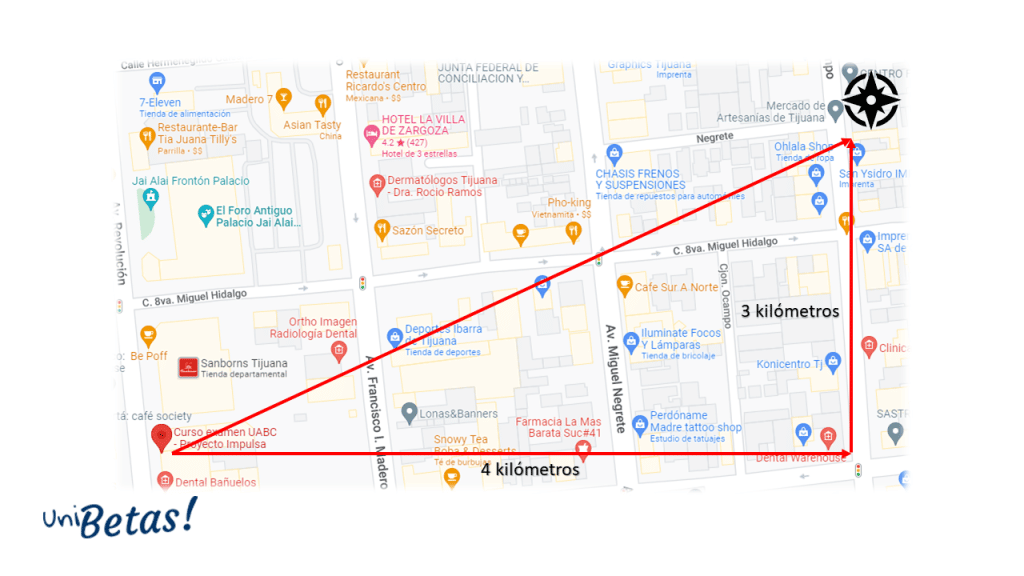
Calculamos la distancia solicitada aplicando la fórmula de la hipotenusa del teorema de Pitágoras.
d=\sqrt{{4}^{2}+{3}^{2}}=5
El destino se encuentra a una distancia rectilínea del vehículo de 5 kilómetros.
Reactivo 8
Una empresa de seguridad se encuentra instalando reflectores de luz desde la azotea de una casa. A último momento, el arquitecto le indicó al encargado de la empresa de seguridad que el área cubierta desde la azotea hasta el suelo debe ser al menos de 7 metros cuadrados.
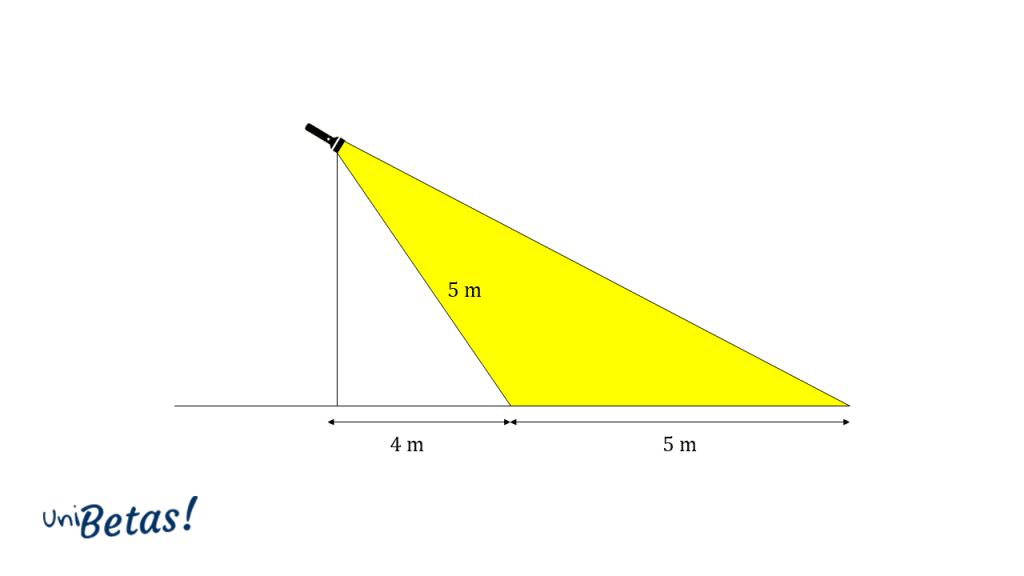
Apoyado en la figura, ¿se cumplen los requerimientos o es necesario cambiar el reflector?
Solución:
Para determinar si se cumplen o no los requerimientos, es necesario calcular el área amarilla que representa la iluminación dada por el reflector. Lo primero que podemos identificar, es que dicha zona amarilla se puede determinar como la resta del área del triángulo rectángulo grande y el área del triángulo rectángulo pequeño (el de color blanco).
{A}_{a}={A}_{tg}-{A}_{tp}
El enunciado no ofrece la altura a la que se encuentra el reflector, pero podemos determinarla aplicando el teorema de Pitágoras, específicamente la fórmula para calcular el cateto restante.
c=\sqrt{{5}^{2}-{4}^{2}}=3 \mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}
Ahora, con la altura determinada, podemos obtener el área cubierta por el reflector.
{A}_{a}=\frac{{b}_{tg}{h}_{tg}}{2}-\frac{{b}_{tp}{h}_{tp}}{2}=\frac{9*3}{2}-\frac{4*3}{2}=\frac{27-12}{2}
{A}_{a}=7.5 {\mathrm{m}}^{2}
El reflector cubre una superficie de 7.5 metros cuadrados, mayor que el mínimo solicitado. Concluimos entonces que no es necesario cambiar el reflector instalado.
Reactivo 9
Las ternas pitagóricas, son grupos de 3 números enteros los cuales satisfacen el teorema de Pitágoras y cuyos valores corresponden a los lados de un triángulo rectángulo. El mismo Pitágoras estudió las ternas y encontró que las mismas pueden generalizarse en función de un parámetro t de la siguiente forma:
\left\{\begin{array}{c}a={t}^{2}-1\\ b=2t\\ c={t}^{2}+1\end{array}\right.
Donde la hipotenusa es la letra c .
En base a las tres ecuaciones anteriores, determine el valor de t que permite obtener a la terna pitagórica más pequeña.
Solución:
Para resolver este problema, solo debemos ir probando valores de t que nos arrojen resultados para a, b y c naturales, es decir, enteros y mayores que cero. Finalmente, comprobaremos que se cumpla el teorema de Pitágoras.
Descartamos probar con 0 y con 1. El primero anula a b y el segundo anula a a . Vamos con t=2 .
t=2
\left\{\begin{array}{c}a={2}^{2}-1=3\\ b=2\left(2\right)=4\\ c={2}^{2}+1=5\end{array}\right.
Comprobamos:
{5}^{2}={4}^{2}+{3}^{2}\to 25=16+9
25=25
Por tanto, la terna pitagórica más pequeña que existe es \left(3, 4, 5\right) . Si analizamos las ecuaciones con algunas desigualdades, descubrimos que, de hecho, se pueden generar ternas pitagóricas siempre que t sea mayor que 1.
Ejercicio 10
Otra utilidad del teorema de Pitágoras, es la caracterización de triángulos en base a su ángulo interno mayor. En base a las siguientes ternas, identifique cuál pertenece a un obtusángulo, cuál a un triangulo rectángulo y cuál a un triángulo acutángulo.
| Terna (a, b, c) |
|---|
| (1, 2, 3) |
| (8, 6, 10) |
| (5, 6, 7) |
Solución:
Primero, debemos recordar las condiciones para verificar que un triángulo sea obtusángulo y acutángulo.
Triángulo obtusángulo.
Triangulo que posee un ángulo interno mayor a 90°. Se verifica que:
{c}^{2}>{a}^{2}+{b}^{2}
Triangulo acutángulo
Triángulo que posee los tres ángulos internos menores a 90°. En este caso se verifica:
{c}^{2}<{a}^{2}+{b}^{2}
Vayamos con la primera terna:
{3}^{2}={1}^{2}+{2}^{2}\to 9>5
Se cumple que {c}^{2}>{a}^{2}+{b}^{2} , este triángulo es obtusángulo.
Segunda terna:
{10}^{2}={8}^{2}+{6}^{2}\to 100=100
Esta terna es Pitagórica y representa los lados de un triángulo rectángulo.
Tercera terna:
{7}^{2}={5}^{2}+{6}^{2}\to 49<61
Para esta última terma se cumple que {c}^{2}<{a}^{2}+{b}^{2} , corresponde a un triángulo acutángulo.
| Terna (a, b, c) | Clasificación |
|---|---|
| (1, 2, 3) | Obtusángulo |
| (8, 6, 10) | Rectángulo |
| (5, 6, 7) | Acutángulo |
Ejercicios propuestos
Puedes practicar los conocimientos adquiridos con los siguientes ejercicios propuestos sobre el Teorema de Pitágoras. Intenta resolverlos por tu cuenta antes de mirar la respuesta correcta.
Ejercicio 1
Calcule el valor de x , para la situación planteada en la imagen.
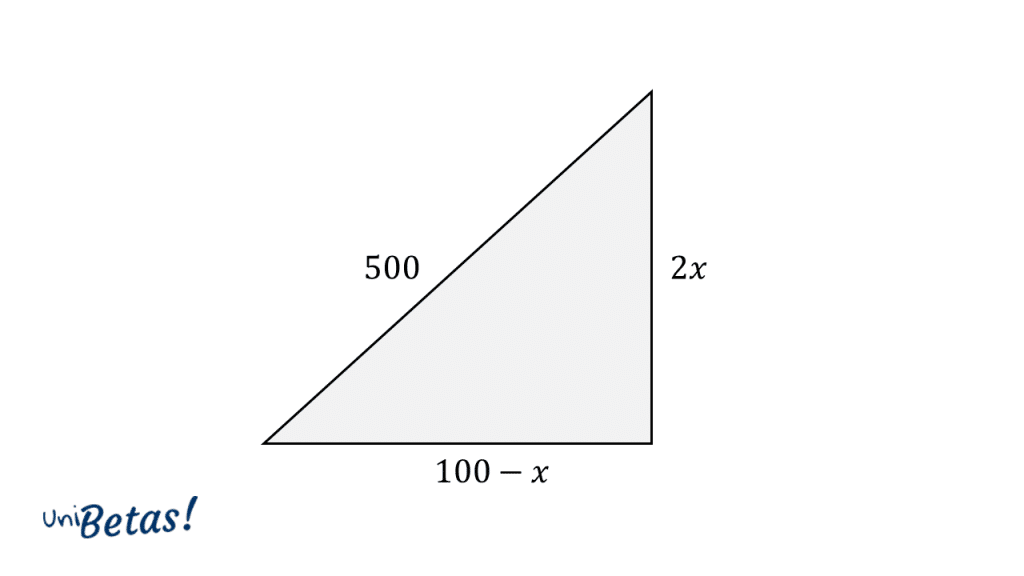
- x=100
- x=221
- x=233
Respuesta correcta: b).
Ejercicio 2
Un estudiante de mecatrónica debe realizar un proyecto que consta en el diseño e implementación de un robot con articulaciones rotoides accionadas por cadena. El motivo de esto, es poder transferir la mayor potencia con una infraestructura lo suficientemente compacta. En la figura se muestran los discos que debe unir con la cadena de transmisión.
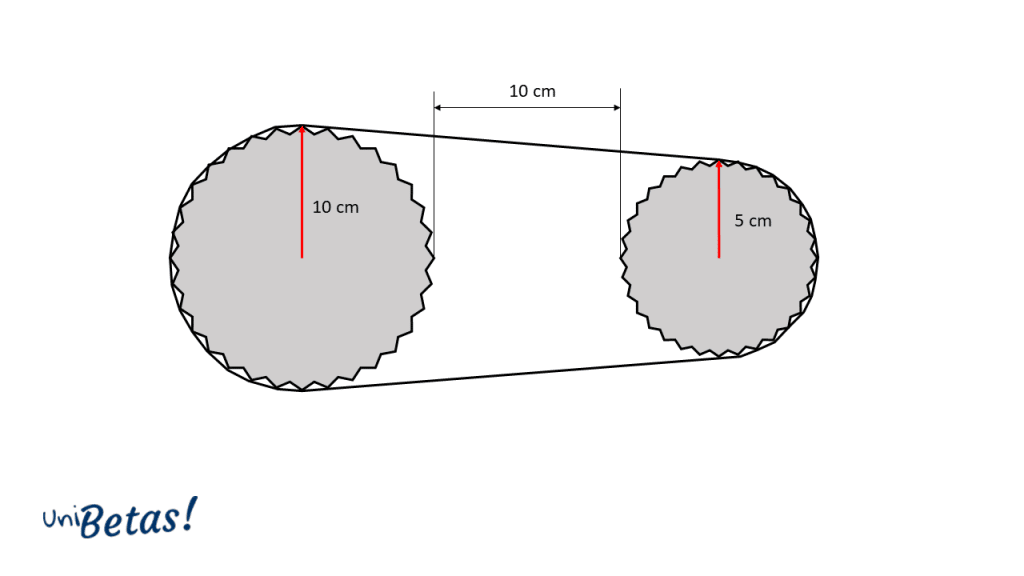
Calcule la longitud aproximada que debe tener la cadena que debe utilizar el estudiante para armar el robot.
- 72.62 \mathrm{c}\mathrm{m}
- 70 \mathrm{c}\mathrm{m}
- 75 \mathrm{c}\mathrm{m}
Respuesta correcta: a).
Ejercicio 3
Se tiene un número complejo el cual tiene como coordenadas 4 en el eje real y 4 en el eje imaginario. Su representación vectorial viene dada por:
z=4+4i
¿Cuál es la representación polar del número complejo dado?
- 4+4i
- 4\sqrt{2}{e}^{i\frac{\pi }{4}}
- 4{e}^{i\frac{\pi }{4}}
Respuesta correcta: b).
Ejercicio 4
Unos investigadores se encuentran cultivando en una placa de Petri una especie de batería desconocida. Durante varios días han recolectado información sobre el crecimiento de las bacterias en la placa, la cual han expresado en mililitros de solución.
Determine:
- ¿Qué tipo de tendencia describe el crecimiento de la población de bacterias?
- ¿Cuánto será la población para el cuarto día?
- Lineal, 22
- Potencial, 22
- Exponencial, 22
Respuesta correcta: a).
Ejercicio 5
Dada la figura de la imagen, determine el valor del área del cuadrado encerrado por los triángulos rectángulos.
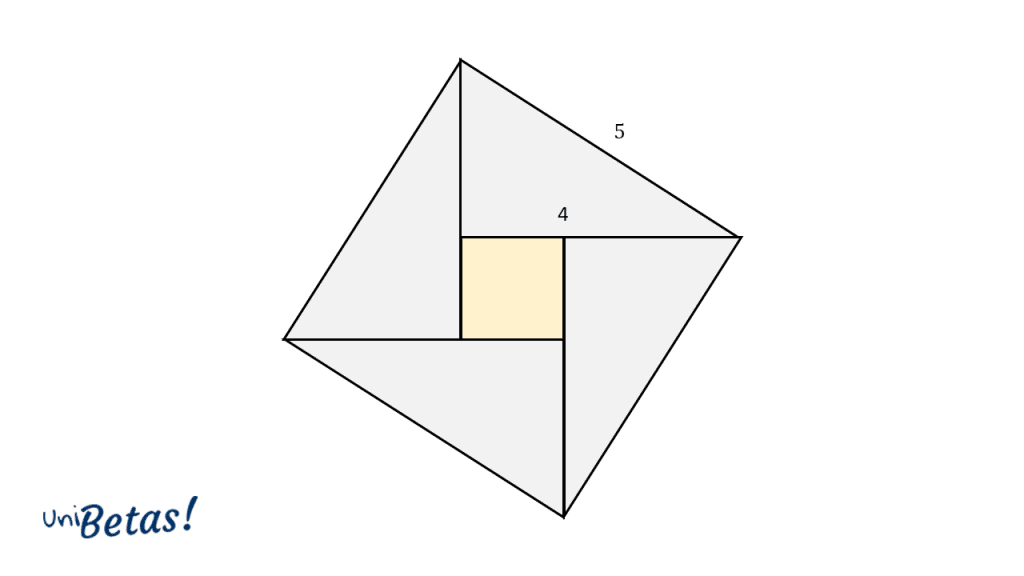
Nota: puedes apoyarte en una de las demostraciones dadas en el apartado teórico de este post.
- 2 unidades cuadradas
- 4 unidades cuadradas
- 1 unidades cuadradas
Respuesta correcta: c).

