Al igual que existe un método para dividir dos números reales cualesquiera conocido como división larga, la división de polinomios es posible y utiliza el mismo algoritmo.

En este post aprenderás a identificar y resolver los diferentes casos de la división polinómica, con ejercicios resueltos paso a paso.
¿Qué es la división de polinomios?
Es una de las 4 operaciones fundamentales entre polinomios. Permite tomar a dos polinomios cualesquiera f(x) y g(x) no nulo para obtener su división.
\frac{f(x)}{g(x)}=q(x)+\frac{r(x)}{g(x)}
Pudiendo expresar al dividendo como:
f(x)=q(x)g(x)+r(x)
Donde:
- f(x): dividendo de la operación
- g(x): divisor de la operación
- q(x): cociente de la operación
- r(x): resto de la operación
Si el resto de la división vale cero, se ha encontrado el cociente exacto para la operación. La división de polinomios es una operación muy útil en algebra, cuando se manejan expresiones polinómicas largas y es un truco (también llamado artificio) muy utilizado en cálculo para facilitar la derivación y la integración.
Casos de la división de polinomios
La división de polinomios puede presentarse en dos formas: un polinomio dividido un número y polinomio dividido polinomio.
Polinomio dividido un número
Es el caso más simple. Solo se divide cada coeficiente de cada término del polinomio por el número en cuestión. Ejemplo:
\frac{8x^2-6x+3}{2}=\frac{8}{2} x^2-\frac{6}{2} x+\frac{3}{2}=4x^2-3x+\frac{3}{2}
Polinomio dividido polinomio
Acá es donde se aplica el algoritmo de división larga que empleamos para dividir números reales. El procedimiento es similar y puede resumirse en la siguiente serie de pasos:
- Dada la división entre los polinomios, ordena cada uno de ellos según el exponente de forma descendente. Si al polinomio está incompleto, se dejan espacios en blanco donde irían dichos términos
\frac{2x^2-x^3+4x+6}{x-1}\rightarrow \frac{-x^3+2x^2+4x+6}{x-1}
- Coloca al polinomio del numerador a la izquierda y al del numerador a la derecha encerado en la clásica cajita de división

- Similar a la división con números reales, debes buscar un monomio que multiplicado por el término de mayor grado del divisor, permita eliminar al término de mayor grado del dividendo. Para este ejemplo, el primer término a eliminar es -x^{3}, si intentas con -x^{2} el termino se cancelaria
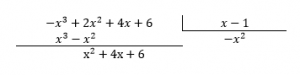
Si al principio te es complicado encontrar el monomio con solo intuición, puedes probar este truco:
monomio=\frac{termino a eliminar dividendo}{termino de mayor grado del divisor}=\frac{-x^3}{x}=-x^2
- Continuamos con el ejemplo
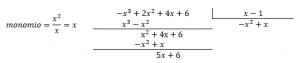

Este resultado es interesante, porque el resto es diferente de cero. Cuando esto sucede, se expresa la división con la forma:
\frac{f(x)}{g(x)} = q(x)+\frac{r(x)}{g(x)}
En este caso:
\frac{-x^3+2x^2+4x+6}{x-1}=-x^2+x+5+\frac{11}{x-1}
Como comprobar el resultado
Es útil en ocasiones comprobar el resultado de una división polinómica, especialmente cuando los polinomios en juego son extensos y con coeficientes fraccionarios, puede dar pie a cometer errores.
Para comprobar el resultado, solo hace falta validar la siguiente igualdad:
f(x)=q(x)g(x)+r(x)
Es decir, comprobar que el dividendo es igual al cociente multiplicado por el divisor sumado con el residuo. Es la misma forma en la que se comprueba una división de números cualquiera. Para ejemplificar, tomemos el ejemplo del punto anterior:
\frac{-x^3+2x^2+4x+6}{x-1}=-x^2+x+5+\frac{11}{x-1}
Donde:
- f(x)=-x^3+2x^2+4x+6
- g(x)=x-1
- q(x)=-x^2+ x+5
- r(x)=11
-x^3+2x^2+4x+6=(x-1)(-x^2+x+5)+11
Se resuelven los productos:
f(x)=x(-x^2+x+5)-(-x^2+x+5)+11
f(x)=-x^3+x^2+5x+x^2-x-5+11
f(x)=-x^3+x^2+x^2+5x-x-5+11
f(x)=-x^3+2x^2+4x+6
Practica lo aprendido con estos ejercicios
Ahora que sabes cómo se realiza la división de polinomios, resuelve el siguiente ejercicio, escoge la opción correcta y comprueba tus nuevos conocimientos. No te preocupes si generas dudas, el problema está resuelto paso a paso.
Obtenga el resultado de la siguiente división de polinomios: \frac{2x^3+3x^2-5x-6}{x+1}
- -6x^2+x+2
- -2x^2-x+6
- 2x^2+x-6
- 6x^2-x-2
Solución:
Paso1: ordena los polinomios en forma descendente según sus exponentes y reescribe la división.

Paso2: encuentra de forma consecutiva los monomios que eliminen al término de mayor grado en el dividendo.
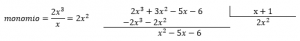
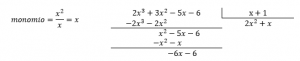
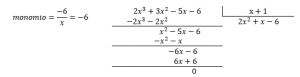
Paso3: culminada la división, obtenemos que el resto es cero. Concluimos que el cociente de ambos polinomios es exacto y se expresa como:
\frac{2x^3+3x^2-5x-6}{x+1}=2x^2+x-6
Según las opciones indicadas en el problema, la correcta seria la c) 2x^2+x-6 .
Continúa practicando y realiza tantos problemas como puedas hasta convertirte en experto. La división de polinomios es un truco que puede sacarte de aprietos al resolver integrales, por lo que vale la pena dedicarle algo de tiempo.


