¡Llegamos a la última parte! Resolvemos la cuarta parte de la guía de probabilidad y estadística IPN, correspondiente a los reactivos desde el 31 al 40.

Continúa estudiando el resto de asignaturas con el material que hemos preparado en la zona de materiales IPN. No olvides incorporar exámenes simulacro en tus jornadas de estudio, monitorea tus tiempos y perfecciónalos antes de la prueba de ingreso.
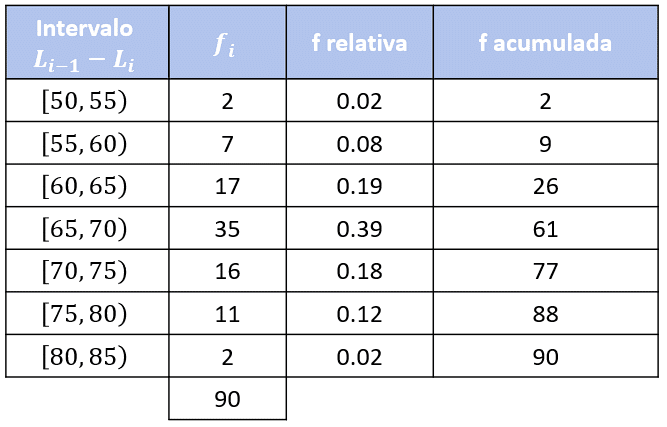
La siguiente tabla de frecuencias reúne información sobre el peso en Kg de 90 empleados de una empresa. Con base en esto, responde las preguntas 30 a 32.
Reactivo 31
¿Cuál es el porcentaje de personas que pesan más de 60 Kg?
- 50%
- 75%
- 85%
- 90%
Solución:
Para calcular el porcentaje de personas que pesan más de 60 kg, debemos sumar el total de personas que hay entre las clases \left[60, 65\right) hasta \left[80, 85\right) . Examinando la tabla, el total de personas es:
\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\left(>60\right)=17+35+16+11+2=81
Finalmente, calculamos el porcentaje como:
P\left(>60\right)=\frac{81}{90}\cdot 100\%=90\%
Concluimos indicando como respuesta correcta al inciso d).
Reactivo 32
Si la frecuencia acumulada es de 77, ¿cuál es el valor total de la frecuencia relativa?
- 50%
- 75%
- 85%
- 86%
Solución:
Examinando los incisos, vemos que el valor de la frecuencia relativa se expresa en forma de porcentaje. Solo debemos dividir la frecuencia acumulada por el total de datos y luego multiplicarlo por 100%.
{F}_{r}=\frac{77}{90}\cdot 100\%=85.55\%
{F}_{r}\approx 86\%
La frecuencia relativa acumulada es del 86%.
La respuesta correcta es la opción d).
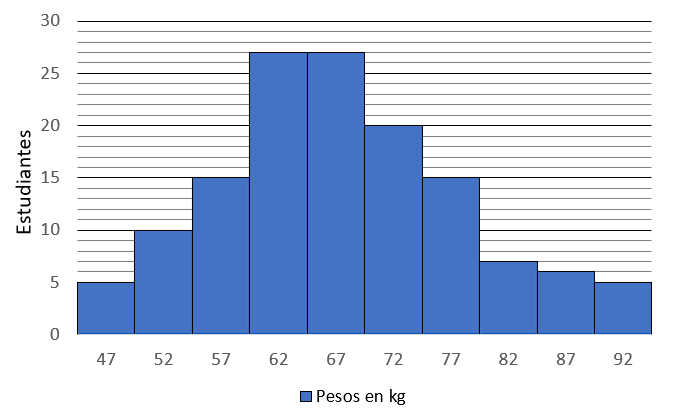
La gráfica presenta información sobre el peso de los estudiantes de un colegio. Con base en esto, responde las preguntas 33 a 35.
Reactivo 33
¿Cuál es el valor de la moda?
- 62.5
- 63.5
- 64.5
- 65.5
Solución:
En estadística, la moda es el valor que más se repite dentro de un conjunto de datos. En este caso, hay dos valores con la misma moda: 62 y 67. La moda en este caso se expresa como el promedio de 62 y 67.
\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{a}=\frac{62+67}{2}=64.5
La moda (en kilogramos) asociada al conjunto de datos es igual a 64.5.
Concluimos que la respuesta correcta es el inciso c).
Reactivo 34
¿Cuál es el valor de la media?
- 67.2
- 67.4
- 67.6
- 67.8
Solución:
La media aritmética se calcula como la suma de los productos de los pesos por su respectiva frecuencia absoluta. Expresemos los datos del gráfico en una tabla de frecuencias para facilitar la solución.
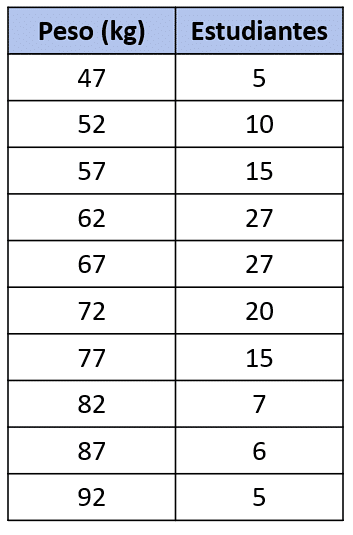
La media aritmética se calcula como:
\stackrel{-}{x}=\frac{\left(47\right)\left(5\right)+\left(52\right)\left(10\right)+\left(57\right)\left(15\right)+\left(62\right)\left(27\right)+\left(67\right)\left(27\right)+\left(72\right)\left(20\right)+\left(77\right)\left(15\right)+\left(82\right)\left(7\right)+\left(87\right)\left(6\right)+\left(92\right)\left(5\right)}{137}=67.47
La media del conjunto de datos es de 67.4 kilogramos.
La respuesta correcta es el inciso b).
Reactivo 35
Determinar el valor de la mediana.
- 61.5
- 62.5
- 63.5
- 64.5
Solución:
Para calcular la mediana, primero escribimos al conjunto de datos en una tabla de frecuencias especificando tanto a la frecuencia relativa como a la relativa acumulada.
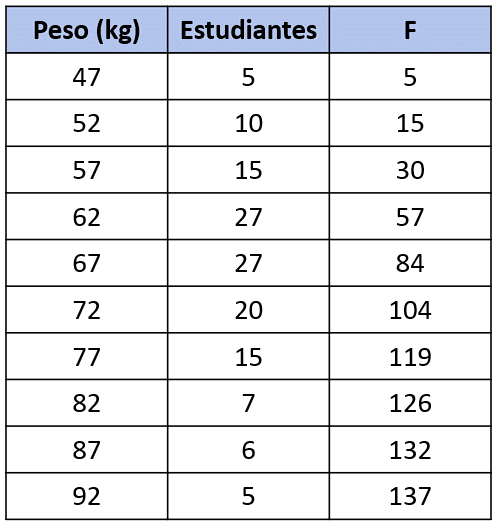
Ahora, dividimos el total de datos entre 2 para obtener la frecuencia de la clase mediana.
{F}_{me}=\frac{137}{2}=68.5
Si buscamos esta frecuencia acumulada en la tabla, veremos que se encuentra entre 62 y 67, cuyas frecuencias acumuladas son de 57 y 84 respectivamente. Por lo tanto, la mediana del conjunto de datos se obtiene como el promedio de los pesos.
Me=\frac{62+67}{2}=64.5
La mediana del conjunto de datos es igual a 64.5 kilogramos.
Seleccionamos como respuesta correcta al inciso d).
Sigue practicando la parte de probabilidad y estadística:
Reactivo 36
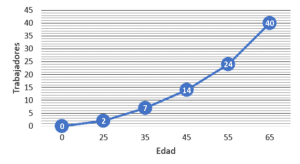
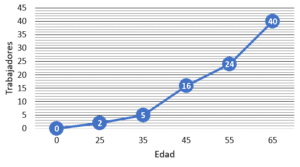
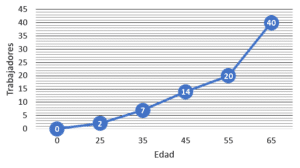
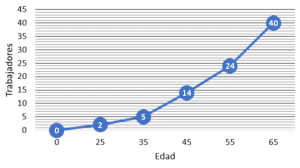
Con base en la siguiente tabla de frecuencias, identificar la gráfica de la ojiva menor que representa la edad de los trabajadores de una empresa.
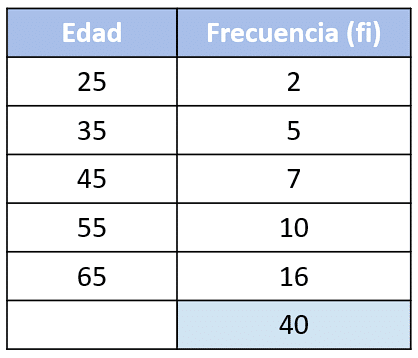
Solución:
Examinando las gráficas, nos daremos cuenta que todas buscan representar la frecuencia absoluta acumulada de los datos. Esto se puede comprobar porque la última edad tiene asignado como número de trabajadores 40, el total del conjunto.
La frecuencia absoluta acumulada de los datos es:
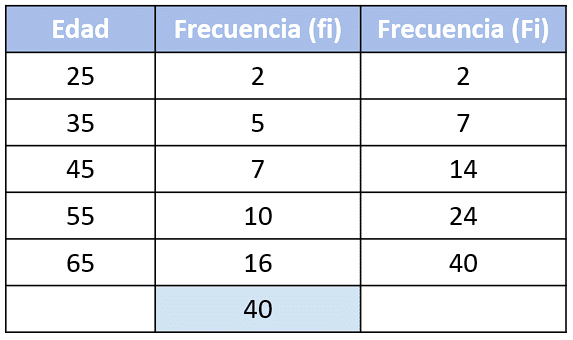
Comparando estas frecuencias acumuladas con los incisos, concluimos que la respuesta correcta es la opción a).
Reactivo 37
Relacionar la fórmula con el tipo de media que le corresponde.

- 1B, 2C, 3A
- 1B, 2A, 3C
- 1A, 2C, 3B
- 1A, 2B, 3C
Solución:
Debemos analizar las fórmulas que se encuentran en la columna izquierda, para relacionarlas con los tipos de media en la derecha. La fórmula del inciso 1 es la que empleamos para el cálculo de la media aritmética: 1B. Descartamos las opciones a y d.
La fórmula del inciso 2 corresponde a la media armónica: 2C. Con esta información: 1B, 2C, … podemos concluir que la respuesta correcta es el inciso a).
Reactivo 38
Determinar la media de \{\mathrm{4,5},\mathrm{6,7},78\} .
- 6
- 7
- 20
- 21
Solución:
La media aritmética se calcula como:
\stackrel{-}{x}=\frac{4+5+6+7+78}{5}=20
La respuesta correcta es el inciso c).
Reactivo 39
Dado el siguiente conjunto de datos, {1,3,5,7,9}, calcular la varianza muestral y la desviación estándar.
- {s}^{2}=11\text{ y }s=\sqrt{11}
- {s}^{2}=10\text{ y }s=\sqrt{10}
- {s}^{2}=9\text{ y }s=3
- {s}^{2}=8\text{ y }s=\sqrt{8}
Solución:
La varianza de la muestra se calcula como:
{s}^{2}=\frac{\sum {\left({x}_{i}-\stackrel{-}{x}\right)}^{2}}{n-1}
Mientras que la desviación estándar es igual a la raíz cuadrada de la varianza. Iniciamos con el cálculo determinando la media de los datos.
\stackrel{-}{x}=\frac{1+3+5+7+9}{5}=5
Ahora calculamos la diferencia entre la media y los datos con ayuda de una tabla.
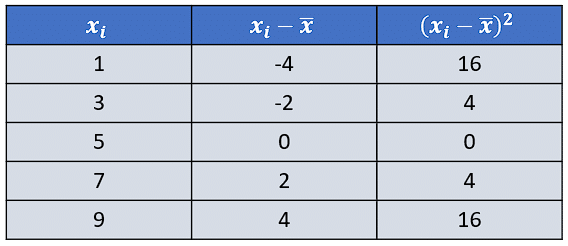
Sustituimos la fórmula de la varianza.
{s}^{2}=\frac{16+4+0+4+16}{5-1}=\frac{40}{4}=10
La desviación estándar:
s=\sqrt{10}
Finalmente:
{s}^{2}=10\text{ y }s=\sqrt{10}
Concluimos el problema indicando como respuesta correcta al inciso b).
Reactivo 40
En un experimento se encontraron datos que corresponden a diferentes tiempos. Determinar el valor de la media.

- 2.2
- 2.4
- 2.6
- 2.8
Solución:
Aplicamos la fórmula de la media aritmética:
\stackrel{-}{x}=\frac{1.1+2.2+3.4+3.2+1.1}{5}=\frac{11}{5}
Finalmente:
\stackrel{-}{x}=2.2
La respuesta correcta es el inciso a).