¡Hola aspirante! En este tutorial vamos a resolver los primeros 10 ejercicios del simulacro examen de admisión de Pensamiento Matemático del nuevo Exani II diseñado por Ceneval.
Aunque los reactivos están resueltos paso a paso, no olvides desarrollarlos por tu cuenta antes de mirar la respuesta correcta. Matemáticas es una asignatura que podrás dominar a través de la práctica y el análisis de cada solución.
Estructura del Exani II
La prueba de ingreso, elaborada por Ceneval, consta de dos grandes partes: la primera, que trata sobre conocimientos generales, también denominada habilidades y conocimientos, y la segunda, acerca de conocimientos específicos.
Los conocimientos generales tienen 30 reactivos de matemáticas (similares a los de este simulacro) y unos 60 de español divididos equitativamente entre comprensión lectora y redacción indirecta.
También existe un examen diagnóstico de inglés, cuya aplicación depende de la universidad y el resultado no afectará tu puntuación final.
En la siguiente tabla contiene un resumen exacto de la estructura de la prueba diseñada por Ceneval.
Conoce la estructura de la guía Exani II y del examen de ingreso
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Temario de pensamiento matemático
Los reactivos de matemáticas en la prueba EXANI cubren una gran cantidad de ramas en esta asignatura tales como aritmética, estadística, geometría, trigonometría y álgebra. No solo basta con aprender las fórmulas, debes entrenar tu capacidad de análisis para resolver problemas con matemáticas.
La parte de pensamiento matemático consta de 30 reactivos en la parte de habilidades y conocimientos. La siguiente lista contiene todos los temas que debes estudiar para responder esta parte del examen.
| Subárea | Tema | Núm. de reactivos |
|---|---|---|
| Comprensión de lo matemático | Conexiones | 18 |
| Estimación | ||
| Sentido numérico | ||
| Matematización | Desarrollo de usos | 12 |
| Lenguaje matemático | ||
| Resignificaciones | ||
| Total | 30 | |
Subárea: Comprensión de lo matemático
- Sentido numérico
- Inecuaciones lineales
- Simplificación de expresiones algebraicas
- Razones trigonométricas
- Área
- Desviación estándar
- Media aritmética
- Conexiones
- Razones y proporciones
- Interpretación gráfica de ecuaciones lineales
- Ejes de simetría
- Estimación de trayectorias
- Frecuencias
- Probabilidad clásica de eventos simples
- Estimaciones
- Leyes de los exponentes
- Porcentaje
- Unidades de medida como patrón de comparación
- Espacio muestral
Subárea: Matematización
- Desarrollo de usos
- Representación gráfica de ecuaciones de segundo grado
- Comportamiento gráfico de funciones cuadráticas
- Relaciones trigonométricas
- Representación gráfica de información
- Medidas de tendencia central y de dispersión
- Lenguaje matemático
- Polinomios
- Sistemas de ecuaciones lineales con dos y tres incógnitas
- Resignificaciones
- Variación lineal tabular
- Medidas de posición (deciles, cuartiles y percentiles)
¿Cómo resolver el examen simulacro?
Estos ejercicios simulacro que hemos diseñado para ti tienen como finalidad ayudarte a dos cosas: a practicar los temas exactos que van para el examen y acortar el tiempo que tardas en resolverlos.
Es importante que incluyas exámenes simulacro en tu calendario de estudios, así pondrás en práctica la teoría y reducirás tus tiempos.
Pon en práctica las siguientes recomendaciones mientras resuelves el examen simulacro, para familiarizarte con la modalidad del examen real.
- Resuelve completa cada parte por tu cuenta antes de mirar las respuestas
- Establece un tiempo no mayor a 20 minutos por cada 10 reactivos
- Analiza el procedimiento que has seguido para resolver los ejercicios y piensa en posibles alternativas que acorten el tiempo
- Asegúrate de tener unos minutos de sobra para comprobar tus respuestas
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico
Ejercicios de Pensamiento Matemático
Luego de esta introducción, vamos con la solución paso a paso de los primeros 10 reactivos tipo selección múltiple del simulacro de Pensamiento Matemático, inspirados en el examen real de Ceneval Exani.
Reactivo 1
Un jugador de billar profesional necesita meter la bola negra que se encuentra cerca del hoyo en la esquina inferior derecha para ganar el torneo mundial. Gracias a su ojo experimentado, sabe que las bolas negra y blanca están a una distancia horizontal de 0.8 metros, además, la blanca está a 0.3 metros del borde superior de la mesa y la negra a 0.5 metros.
Para introducir la bola, debe realizar un tiro en la banda superior. Apoyado en la imagen ¿Cuál debería ser el ángulo de disparo \alpha , medido desde la horizontal para realizar el tiro con éxito?
Considera que el ángulo de impacto es igual al ángulo de repulsión de la bola.
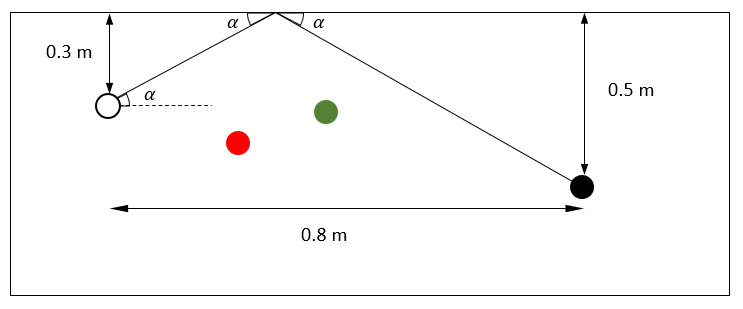
- 45°
- 30°
- 66°
Solución:
Para resolver este ejercicio, debemos pensarlo como un problema de trigonometría. En base a esto, de la figura podemos observar que se forman dos triángulos, digamos que ABC y DEF . En la siguiente imagen se indican dichas figuras.
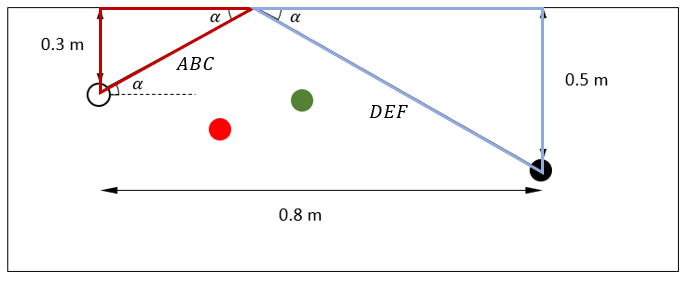
La primera relación que podemos observar, es que ambos tienen un ángulo interno \alpha cuyo valor es el que necesita conocer el jugador para ganar la final. Además, observando la base de ambos triángulos, nos daremos cuenta que la suma de ambas bases es igual a la distancia entre las bolas, es decir, 0.8 metros.
Si llamamos a la base del triángulo ABC x y a la del DEF y , podemos decir que:
x+y=0.8
De todas las identidades trigonométricas, la tangente de \alpha nos permitirá relacionar la base de los triángulos con sus respectivos ángulos conocidos.
Para el triángulo ABC .
\mathrm{tan}\alpha =\frac{0.3}{x}
Para el triángulo DEF .
\mathrm{tan}\alpha =\frac{0.5}{y}
Despejamos a x y y para obtener:
x=\frac{0.3}{\mathrm{tan}\alpha }
y=\frac{0.5}{\mathrm{tan}\alpha }
Sustituimos en la primera fórmula deducida.
x+y=0.8\to \frac{0.3}{\mathrm{tan}\alpha }+\frac{0.5}{\mathrm{tan}\alpha }=0.8
Despejamos tangente de alfa.
\frac{0.3}{\mathrm{tan}\alpha }+\frac{0.5}{\mathrm{tan}\alpha }=0.8\to \frac{0.8}{\mathrm{tan}\alpha }=0.8
\mathrm{tan}\alpha =\frac{0.8}{0.8}=1\to \mathrm{tan}\alpha =1
Para que la tangente valga la unidad, el ángulo alfa debe ser igual a 45°, por lo tanto:
\alpha =45°
Concluimos que el jugador debe tirar a un ángulo igual a 45° para ganar la final. Comparando con las opciones, la respuesta correcta es la a).
Reactivo 2
Calcula el área sombreada en la figura dentro del cuadrado.
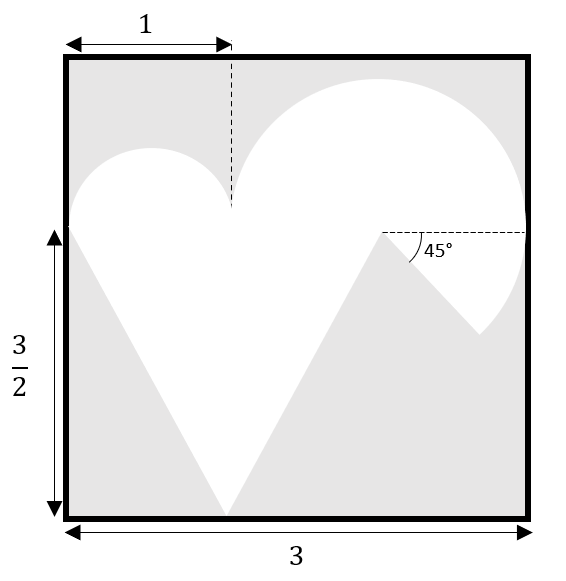
- \frac{2}{15}-\frac{4}{3}\pi
- \frac{15}{2}-\frac{3}{4}\pi
- 2-4\pi
Solución:
Para calcular el área sombreada en la figura, debemos calcular el área del cuadrado y a esta, restarle el área que conforman las figuras en color blanco.
{A}_{s}={A}_{c}-{A}_{b}
Ahora, la tarea es determinar el área de la figura en color blanco, para ello, tenemos que identificar figuras comunes que la conformen, calcular el área de cada una de ellas y sumarlas para obtener el área blanca total.
Examinando la imagen, se pueden identificar: un triángulo, dos semicírculos y una sección circular de 45°. A continuación, la división de las figuras.
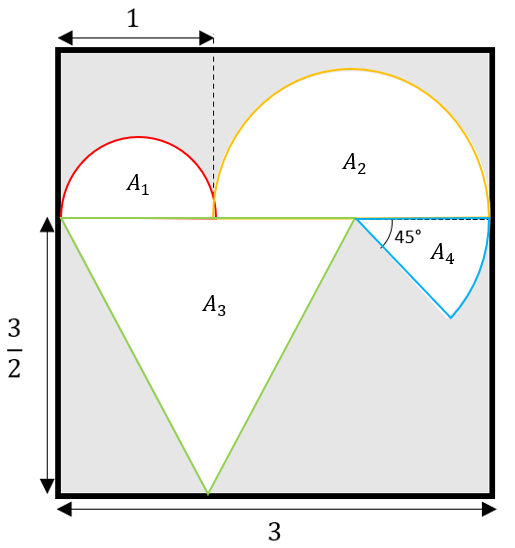
Las áreas 1 y 2 son semicírculos, el área 3 un triángulo y el área 4 un octavo de círculo. Por tanto:
{A}_{b}={A}_{1}+{A}_{2}+{A}_{3}+{A}_{4}
El área de medio círculo es \frac{\pi {r}^{2}}{2} , el de un octavo de círculo \frac{\pi {r}^{2}}{8} y el área de un triángulo es \frac{bh}{2} .
{A}_{b}=\frac{\pi {r}_{1}^{2}}{2}+\frac{\pi {r}_{2}^{2}}{2}+\frac{{b}_{3}{h}_{3}}{2}+\frac{\pi {r}_{4}^{2}}{8}
El valor de los radios, base y altura del triángulo son:
{r}_{1}=\frac{1}{2};{r}_{2}=1;{b}_{3}=2;{h}_{3}=\frac{3}{2};{r}_{4}=1
Sustituimos en la ecuación.
{A}_{b}=\frac{\pi {\left(\frac{1}{2}\right)}^{2}}{2}+\frac{\pi {\left(1\right)}^{2}}{2}+\frac{\left(2\right)\left(\frac{3}{2}\right)}{2}+\frac{\pi {\left(1\right)}^{2}}{8}=\frac{3}{4}\pi +\frac{3}{2}
Regresando a la primera ecuación del problema, solo nos falta encontrar el área del cuadrado {A}_{c} .
{A}_{c}={l}^{2}={3}^{2}=9
Sustituimos y simplificamos.
{A}_{s}=9-\frac{3}{4}\pi -\frac{3}{2}=\frac{15}{2}-\frac{3}{4}\pi
Comparando con las opciones, la respuesta correcta es la b).
Reactivo 3
Simplifica la expresión algebraica:
\frac{7\left({x}^{2}+x-6\right)}{\left({x}^{2}-4x+4\right)\left({x}^{2}-9\right)}
- \frac{14}{3{x}^{2}-2}
- \frac{1}{x-3}
- \frac{7}{{x}^{2}-5x+6}
Solución:
Para encontrar la forma simplificada de la expresión algebraica, debemos factorizar a los polinomios del numerador y del denominador.
El numerador, en este caso, es un polinomio de segundo grado multiplicado por el número 7. Debemos buscar dos números que sumados den 1 y que multiplicados den -6, evidentemente son 3 y -2.
3+\left(-2\right)=1 y 3*\left(-2\right)=6
Reescribiendo al polinomio:
{x}^{2}+x-6=\left(x+3\right)\left(x-2\right)
Aplicamos el mismo razonamiento con el polinomio de segundo grado del numerador. Los números en cuestión son -2 y -2.
-2-2=-4 y \left(-2\right)\left(-2\right)=4
Reescribiendo:
{x}^{2}-4x+4=\left(x-2\right)\left(x-2\right)
Al binomio del denominador aplicamos diferencia de cuadrados.
{x}^{2}-9={x}^{2}-{3}^{2}=\left(x+3\right)\left(x-3\right)
Sustituimos todo en la expresión original.
\frac{7\left(x+3\right)\left(x-2\right)}{\left(x-2\right)\left(x-2\right)\left(x+3\right)\left(x-3\right)}
Simplificamos.
\frac{7\left(x+3\right)\left(x-2\right)}{\left(x-2\right)\left(x-2\right)\left(x+3\right)\left(x-3\right)}=\frac{7}{\left(x-2\right)\left(x-3\right)}
Desarrollamos el producto de binomios en el denominador.
\frac{7}{\left(x-2\right)\left(x-3\right)}=\frac{7}{{x}^{2}-5x+6}
Finalmente:
\frac{7\left({x}^{2}+x-6\right)}{\left({x}^{2}-4x+4\right)\left({x}^{2}-9\right)}=\frac{7}{{x}^{2}-5x+6}
Concluimos que la respuesta correcta es la opción c).
Reactivo 4
En una empresa, el capital para la compra de inventario (CI) de almacén debe ser al menos 1.22 veces la demanda de mercado (DM) sumada una reserva de 12000$ pesos. Encuentra:
- La inecuación que representa el modelo financiero
- Suponiendo que la demanda de mercado, estimada por los analistas de la empresa, es de 134,550$ pesos, calcule el mínimo capital de inventario de la empresa
- DM\le 1.22CI-12000 y CI mínimo de 1,000,000$
- CI\ge 1.22DM+12000 y CI mínimo de 176,151$
- \frac{CI}{1.22}+12000=DM y CI mínimo de 200,000$
Solución:
Para encontrar el modelo financiero y el valor solicitado, debemos transformar la inecuación dicha en lenguaje natural a lenguaje matemático. Analicemos esta primera frase del enunciado:
…el capital para la compra de inventario (CI) de almacén debe ser al menos 1.22 veces la demanda de mercado (DM)…
Que puede escribirse como:
CI\ge 1.22DM
La siguiente parte de la frase nos dice:
… sumada una reserva de 12000$ pesos.
Es decir, a las 1.22DM le sumamos 12000$ pesos.
CI\ge 1.22DM+12000
Lista la primera parte, ahora podemos calcular el capital de inventario necesario a partir del valor de demanda de mercado dado.
DM=134550\to CI\ge 1.22\left(134550\right)+12000
\therefore CI\ge 176151
Juntando ambas soluciones concluimos:
CI\ge 1.22DM+12000 y CI mínimo de 176,151$
Comparando con las opciones, la respuesta correcta es la b).
Reactivo 5
Los analistas de una firma financiera han estimado las curvas de oferta y demanda para una empresa telefónica que está por iniciar sus operaciones. Las curvas representadas por dos rectas son:
Q=100+6P
Q=550-4P
Indica las coordenadas del punto de equilibrio del mercado.
- Q=370, P=45
- Q=39, P=394
- Q=34, P=98
Solución:
El punto de equilibrio de mercado viene dado por el punto de intersección entre las rectas de oferta y demanda. En este caso, debemos resolver el sistema de dos ecuaciones y dos incógnitas señaladas.
Q=100+6P
Q=550-4P
En este punto puedes emplear el método de tu preferencia. Para fines de este ejercicio, usaremos el método por reducción. Multiplicamos la primera ecuación por -1.
-{E}_{1}:-Q=-100-6p
Ahora, hacemos la operación {E}_{1}+{E}_{2} .
-Q=-100-6P
Q=550-4P
0=450-10P
\therefore P=45
Sustituimos este resultado en {E}_{2} para obtener a Q .
Q=550-4\left(45\right)=370
Finalmente, el punto de equilibrio de mercado es:
Q=370 y P=45
Respuesta correcta: a).
Reactivo 6
Juan, Luis y Lupe son tres primos que debaten sobre cuál de los tres tiene el grupo de amigos con edades más variadas. ¿Con qué parámetro estadístico podrían Juan, Lupe y Luis determinar quién tiene el grupo de amigos con edades más dispersas?
- Desviación estándar
- Media aritmética
- Percentil
Solución:
Teniendo en cuenta los tres parámetros estadísticos de las 3 opciones, el único que permite medir el grado de dispersión de un conjunto de datos es la desviación estándar. Por su parte, la media aritmética es una medida de tendencia central y el percentil una medida de localización.
Concluimos seleccionando como respuesta correcta la opción a).
Reactivo 7
En la siguiente tabla, se muestran las estadísticas de goles anotados durante los primeros 5 partidos de la temporada para los 3 mejores jugadores de la liga.
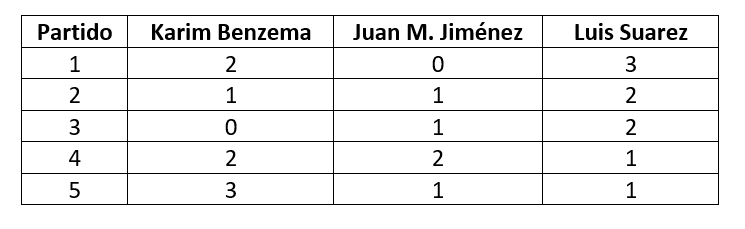
Ordena de forma ascendente a los jugadores, en función de su promedio de goles por partido.
- Benzema < Juan < Luis
- Luis < Juan < Benzema
- Juan < Benzema < Luis
Solución:
En este caso, solo debemos calcular la media aritmética de los goles anotados por partido de cada jugador y, en base a los resultados, ordenarlos de menor a mayor.
Karim Benzema
{\stackrel{-}{g}}_{kb}=\frac{2+1+0+2+3}{5}=1.6
Juan M. Jiménez
{\stackrel{-}{g}}_{jmj}=\frac{0+1+1+2+1}{5}=1
Luis Suarez
{\stackrel{-}{g}}_{ls}=\frac{3+2+2+1+1}{5}=1.8
Ordenados en forma creciente quedarían:
Juan < Benzema < Luis
La respuesta correcta es la opción c).
Reactivo 8
Determine el valor de x , si la longitud del segmento AD=20 m y BC=5 m . Considera además que la relación entre los segmentos AB y CD es \frac{2}{3} .
\frac{AB}{CD}=\frac{2}{3}
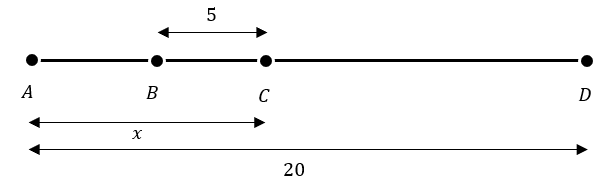
- x=6 \mathrm{m}
- x=5 \mathrm{m}
- x=11 \mathrm{m}
Solución:
Para calcular el valor de x , debemos plantear ecuaciones hasta que tengamos: un sistema homogéneo o una ecuación con una incógnita para despejar de forma directa. Comenzamos indicando que la suma de los 3 segmentos es igual al segmento mayor:
AB+BC+CD=AD=20
\therefore AB+BC+CD=20
Por otro lado x es igual a AB sumado BC .
x=AB+BC
Si BC=5 , entonces:
x=AB+5
Sustituyendo x en la primera ecuación obtenemos que:
x+CD=20
Si \frac{AB}{CD}=\frac{2}{3} podemos sustituir CD o AB en una de las ecuaciones. Escogemos hacerlo con CD .
CD=\frac{3}{2}AB
Sustituyendo en la ecuación 2:
x+\frac{3}{2}AB=20
Tenemos ahora un sistema homogéneo de 2×2. Despejamos a AB en ambas ecuaciones.
x=AB+5\to AB=x-5
x+\frac{3}{2}AB=20\to AB=\frac{2}{3}\left(20-x\right)
Igualamos.
x-5=\frac{2}{3}\left(20-x\right)
Despejamos a x .
3x-15=40-2x\to 3x+2x=40+15
\therefore 5x=55\to x=11 \mathrm{c}\mathrm{m}
Comparando con las opciones, indicamos como correcta la opción c).
Reactivo 9
Jesús, Fernando y Paco han aplicado para trabajar como pintores en una construcción, pero solo hay lugar para uno de ellos. El contratista necesita la mayor eficiencia, por lo que ha decidido someterlos a una prueba midiendo la superficie que pueden pintar en un determinado tiempo. Luego de las pruebas, los resultados son los siguientes:

Determina cuál aspirante puede cubrir la mayor superficie por minuto.
- Jesús
- Fernando
- Paco
Solución:
Para medir este parámetro, debemos calcular el cociente de metros cuadrados pintados por minuto de cada aspirante y quien tenga el mayor cociente, se queda con el trabajo. Vamos a realizar los cálculos.
Jesús=\frac{15{\mathrm{m}}^{2}}{20\mathrm{m}\mathrm{i}\mathrm{n}}=0.75 {\mathrm{m}}^{2}/\mathrm{m}\mathrm{i}\mathrm{n}
Fernando=\frac{12{\mathrm{m}}^{2}}{15\mathrm{m}\mathrm{i}\mathrm{n}}=0.8 {\mathrm{m}}^{2}/\mathrm{m}\mathrm{i}\mathrm{n}
Paco=\frac{20{\mathrm{m}}^{2}}{22\mathrm{m}\mathrm{i}\mathrm{n}}=0.91 {\mathrm{m}}^{2}/\mathrm{m}\mathrm{i}\mathrm{n}
Finalmente, indicamos que Paco es capaz de cubrir mayor área por minuto.
La respuesta correcta es la c).
Reactivo 10
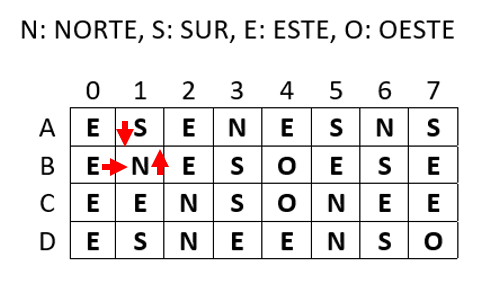
La siguiente tabla posee en cada casilla la dirección en la que se debe avanzar en el siguiente paso. ¿A través de qué casilla se debe ingresar a la tabla para ir de derecha a izquierda? Indica fila y columna.
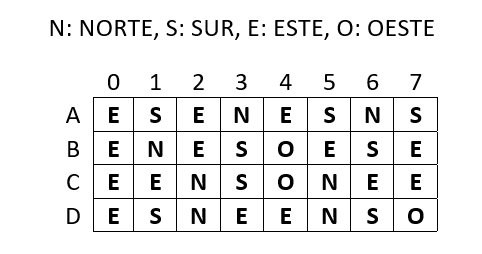
- A0
- D0
- C0
Solución:
Para conseguir la casilla que nos permite llegar del borde izquierdo al derecho, debemos probar una a una hasta que logremos formar el camino respectivo, siguiendo las reglas de movimiento impuestas por cada casilla.
Comenzamos por la casilla A0, que nos indica ir al este, luego A1 al sur y el recorrido se queda trabado, porque B1 nos indica ir hacia arriba de nuevo, hemos entrado en un bucle sin salida.
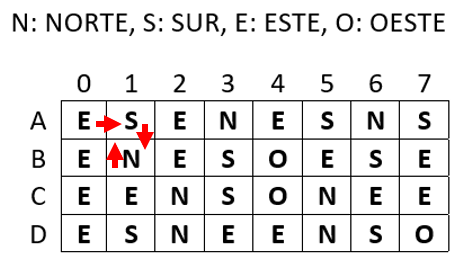
El mismo caso se da para la casilla B0. Primero vamos al este, en B1 al norte hacia A1 y luego de nuevo a B1 y el recorrido se tranca en un bucle.
En la casilla C0 avanzamos al este, luego en C1 de nuevo al este. En C2 al norte llegando a B2, avanzamos a B3 y allí hasta C3 y luego a D3, para continuar a la casilla D4. En D4 vamos a D5, luego C5 y de nuevo hacia arriba a B5. Ahora a B6, luego a C6, C7 y finalmente salimos de la cuadrícula.
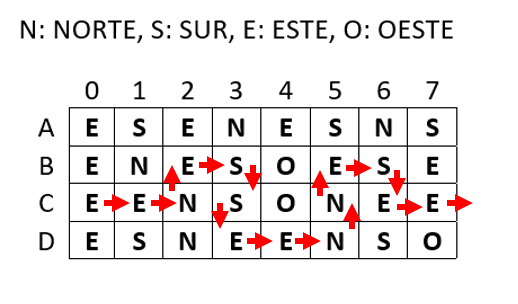
Concluimos entonces que la respuesta correcta es la opción c).


