Continúa con la solución de la segunda parte de la guía de física, reactivos del 11 al 20, para el área de Ingeniería y Ciencias Físico Matemáticas como preparación al examen de ingreso al IPN.

Física es una asignatura central durante la carrera y vida profesional de un Ingeniero. Tómate el tiempo necesario para comprender los conceptos básicos y domina física, ¡como todo un crack!
Reactivo 11
Considerar un objeto de masa m = 2 kg atado a un resorte cuya constante es k=50 N/m y que oscila en movimiento armónico simple sobre un riel de aire horizontal. ¿Cuál será la velocidad máxima de m, si la máxima elongación del resorte es 10 cm?
- 0.5\mathrm{m}/\mathrm{s}
- 0.9\mathrm{m}/\mathrm{s}
- 10.2\mathrm{m}/\mathrm{s}
- 50.1\mathrm{m}/\mathrm{s}
Solución:
Desde el punto de vista fundamental, deberíamos plantear la segunda ley de Newton para el sistema masa-resorte y resolver la ecuación diferencial resultante. Vamos analizar el problema para evitar resolver la ecuación diferencial y recurrir a ella solo cuando sea necesario.
La segunda ley de Newton nos dice que la aceleración que experimenta un cuerpo es igual al cociente entre la fuerza resultante aplicada y su masa.
a=\frac{F}{m}
En este caso, tenemos el valor de la masa, mientras que la fuerza se puede calcular aplicando la ley de Hooke.
a=-\frac{k\mathrm{\Delta }x}{m}
Tanto k como m son constantes por otro lado, la aceleración es directamente proporcional a la elongación del resorte. Esto quiere decir que la máxima aceleración se obtiene cuando se aplica la máxima elongación. Antes de continuar, debemos señalar un detalle importante para el análisis.
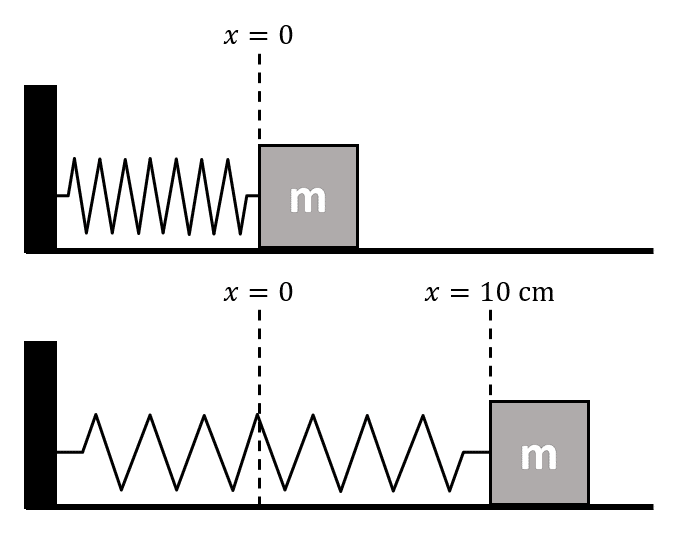
La máxima elongación ocurre por la extensión o compresión del resorte respecto al punto de equilibrio. Es decir, la elongación máxima se mide desde el punto de equilibrio.
Otra cosa importante, es que en el MAS de un sistema masa-resorte la máxima velocidad ocurre en el punto de equilibrio, mientras que la máxima aceleración ocurre en los puntos de elongación. Por esta razón, la amplitud de la aceleración es igual a la aceleración máxima.
Gracias a esto y debido a que este MAS es oscilatorio puro, la aceleración debe tener la forma:
a\left(t\right)=\frac{k\mathrm{\Delta }x}{m}\mathrm{sin}\left(\omega t+\varphi \right)
Donde \frac{k\mathrm{\Delta }x}{m} es la amplitud de la aceleración o máxima aceleración, \omega es la frecuencia angular y \varphi es la fase inicial del movimiento. En este caso solo nos interesa determinar a \omega . Si nos remontamos a la ecuación diferencial del movimiento:
\frac{{d}^{2}x}{d{t}^{2}}+\frac{k}{m}x=0
Podemos obtener el valor de \omega si sustituimos a la aceleración en la ecuación diferencial. Nota: A=\frac{k\mathrm{\Delta }x}{m} para simplificar cálculos.
\frac{{d}^{2}x}{d{t}^{2}}+\frac{k}{m}x=0\to -{\omega }^{2}A\mathrm{sin}\left(\omega t+\varphi \right)+\frac{k}{m}A\mathrm{sin}\left(\omega t+\varphi \right)=0
Nos queda:
{\omega }^{2}=\frac{k}{m}\to \omega =\sqrt{\frac{k}{m}}=\sqrt{\frac{50}{2}}=\sqrt{25}=5 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}
\omega =5 \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}
Ahora, recordando la relación entre la velocidad y la aceleración de un cuerpo:
v\left(t\right)=\int a\left(t\right)dt
Integrando a la aceleración:
v\left(t\right)=\frac{k\mathrm{\Delta }x}{m}\int \mathrm{sin}\left(\omega t+\varphi \right)dt=-\frac{k\mathrm{\Delta }x}{\omega m}\mathrm{cos}\left(\omega t+\varphi \right)
La velocidad máxima es igual a la amplitud de la función velocidad.
{v}_{m}={A}_{v}=\frac{k\mathrm{\Delta }x}{\omega m}
Sustituimos los valores. La elongación se sustituye en metros.
{v}_{m}=\frac{\left(50\right)\left(0.1\right)}{\left(5\right)\left(2\right)}=0.5 \mathrm{m}/\mathrm{s}
La máxima velocidad del bloque es igual a 0.5 metros por segundo.
Comparando con los incisos, la respuesta correcta es el a). Acotamos que la solución ha sido extensa para intentar explicar cada detalle. Estos temas suelen encontrarse en libros universitarios y con explicaciones muy técnicas.
En lugar de solo colocar una fórmula y resolver, hemos dejado esta explicación que solo pretende ser ilustrativa, sin entrar en temas de ecuaciones diferenciales y sus soluciones. Recuerda que en Unibetas Pro tenemos cursos en los que explicamos a fondo todos los temas del examen.
Reactivo 12
Un tinaco contiene una capa de aceite de 0.1 m sobre 1.2 m de agua. Si la densidad del aceite es de 700\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} y la del agua es de 1000\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} , ¿cuál es la presión manométrica en la interfaz aceite-agua? Considerar g=9.81\mathrm{m}/{\mathrm{s}}^{2} .
- 68.7 Pa
- 382.7 Pa
- 589.7 Pa
- 686.7 Pa
Solución:
Debemos aplicar la ecuación de presión hidrostática para resolver el problema. Hagamos un dibujo ilustrativo del problema. El agua queda en la parte inferior mientras que el aceite asciende a la superficie, esto porque el agua tiene mayor densidad.
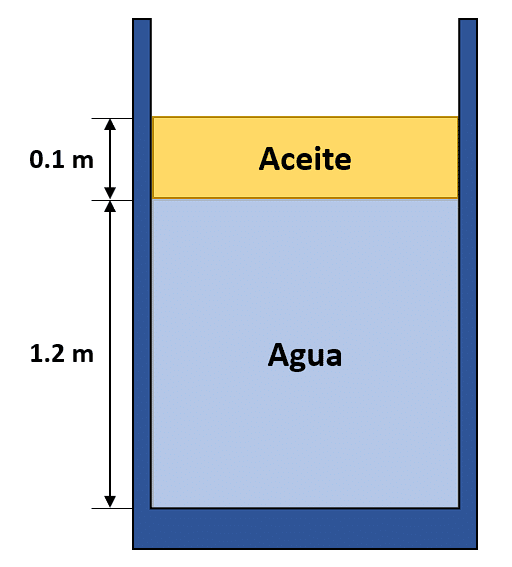
La presión en la interfaz aceite – agua es igual a la presión generada por la columna aceite.
{P}_{I}={P}_{Oil}
Sustituimos en ambos casos la ecuación de presión hidrostática.
{P}_{h}=\rho \cdot g\cdot \mathrm{\Delta }h
Donde \rho es la densidad de la sustancia, g es la aceleración de la gravedad y \mathrm{\Delta }h es la altura de la columna de líquido. Sustituimos en la ecuación y calculamos.
{P}_{T}=\left(700\right)\left(0.1\right)\left(9.81\right)=686.7 \mathrm{P}\mathrm{a}
La presión en la interfaz aceite – agua es de 686.7 Pascales.
La respuesta correcta es el inciso d).
Reactivo 13
Encontrar la altura a la que deberá estar lleno un tanque de almacenamiento de agua (sin tapa) para que, a través de un orificio en el fondo de este, el agua salga con una velocidad de 19.62\mathrm{m}/\mathrm{s} . Considerar g=9.81\mathrm{m}/{\mathrm{s}}^{2} .
- 96m
- 95m
- 62m
- 55m
Solución:
Para resolver este problema, aplicamos la ecuación de Bernoulli.
{P}_{1}+\frac{1}{2}\rho {v}_{1}^{2}+\rho g{h}_{1}={P}_{2}+\frac{1}{2}\rho {v}_{2}^{2}+\rho g{h}_{2}
Realizamos un dibujo de la situación planteada para identificar los puntos de interés.
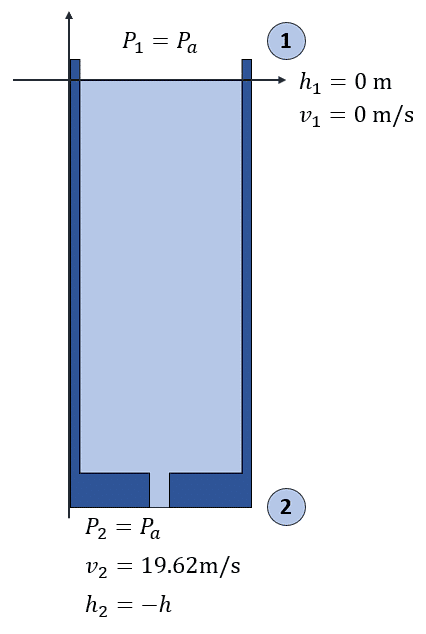
Colocando el sistema de referencia en la parte superior del tanque, tenemos que la altura {h}_{1}=0 \mathrm{m} , mientras que {h}_{2}=-h . Por otra parte, la velocidad del fluido en la parte más alta es de 0 metros por segundo, mientras que en la zona inferior es de 19.62\mathrm{m}/\mathrm{s} . La presión en ambos puntos es la atmosférica.
Sustituimos en la ecuación de Bernoulli.
{P}_{a}+\frac{1}{2}\rho {\left(0\right)}^{2}+\rho g\left(0\right)={P}_{a}+\frac{1}{2}\rho {v}_{2}^{2}+\rho g\left(-h\right)
Simplificamos.
0=\frac{1}{2}\rho {v}_{2}^{2}-\rho gh\to h=\frac{{v}_{2}^{2}}{2g}
Evaluamos.
h=\frac{{\left(19.62\right)}^{2}}{2\left(9.81\right)}=19.62 \mathrm{m}
Para que la velocidad de escape del agua sea de 19.62\mathrm{m}/\mathrm{s} , la altura del tanque debe ser de 19.62 \mathrm{m} . La respuesta correcta es el inciso c).
Reactivo 14
La lectura de un amperímetro marca 0.3 A, mientras que la de un voltímetro es de 1.5 V. Señalar el valor de la resistencia, si el amperímetro y el voltímetro son ideales.
- 4\mathrm{\Omega }
- 3\mathrm{\Omega }
- 5\mathrm{\Omega }
- 6\mathrm{\Omega }
Solución:
En circuitos eléctricos, cuando se indica que los instrumentos de medida son ideales, significa que sus resistencias internas son despreciables, que no presentan caída de tensión y que no tienen consumo de corriente.
Teniendo en cuenta esto, la corriente y la tensión medidas corresponden a los valores de consumo reales de la carga. Podemos calcular la resistencia aplicando la Ley de Ohm.
R=\frac{V}{I}=\frac{1.5}{0.3}=5 \mathrm{\Omega }
La resistencia es de 5 Ohm.
Concluimos seleccionando como respuesta correcta al inciso c).
Reactivo 15
Calcular la energía en Joules que consume un foco de 50W si se mantiene encendido durante dos horas.
- 360 J
- 3600 J
- 36000 J
- 360000 J
Solución:
La potencia es la energía consumida por una carga en un intervalo de tiempo t .
P=\frac{E}{t}
Para calcular la energía consumida, multiplicamos la potencia por el tiempo.
E=P\cdot t
El tiempo debe estar expresado en segundos. 2 horas equivalen a 7200 segundos.
E=\left(50\right)\left(7200\right)=\mathrm{360,000} \mathrm{J}
El foco consume 360,000 Joules durante las dos horas que permanece encendido.
La respuesta correcta es el inciso d).
Reactivo 16
Se hace una aleación de oro y cobre en proporciones desconocidas para formar un lingote con dimensiones de 40 cm x 20 cm x 8cm y masa de 16 kg. Calcular la densidad de la aleación {\mathcal{l}}_{L} .
- 120\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}
- 1200\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}
- 2500\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}
- 12000\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}
Solución:
La densidad de cualquier cuerpo se calcula como el cociente entre la masa y el volumen que ocupa. El volumen debe estar expresado en metros cúbicos y la masa en kilogramos.
Calculamos el volumen aplicando la fórmula para el volumen de un paralelepípedo.
v=a\times h\times l
Sustituimos las dimensiones en metros.
v=\left(0.4\right)\left(0.2\right)\left(0.08\right)=0.0064 {\mathrm{m}}^{3}
Calculamos la densidad.
\rho =\frac{m}{V}=\frac{16}{0.0064}=2500\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}}
La densidad del bloque hecho con la aleación es de 2500\mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} .
Indicamos como respuesta correcta al inciso c).
Reactivo 17
Un objeto registró una temperatura de 45 °C. ¿A cuánto equivale esta en la escala Fahrenheit?
- 23°F
- 48.4°F
- 99.4°F
- 113°F
Solución:
Para transformar de Celsius a Fahrenheit se utiliza la siguiente ecuación.
{T}_{F}=\frac{9}{5}{T}_{c}+32
Sustituimos.
{T}_{F}=\frac{9}{5}\left(45\right)+32=113 °\mathrm{F}
La respuesta correcta es el inciso d).
Reactivo 18
Señalar la cantidad de calor que debe suministrarse a 500 g de aluminio para elevar su temperatura de 40 °C hasta 180 °C. El calor específico del aluminio es: 0.212\mathrm{c}\mathrm{a}\mathrm{l}/{\mathrm{g}}^{\circ }\mathrm{C} .
- 1187 cal
- 1872 cal
- 14840 cal
- 18720 cal
Solución:
La capacidad calorífica se calcula como:
c=\frac{Q}{m\left({T}_{2}-{T}_{1}\right)}
Despejamos a la cantidad de calor Q .
Q=mc\left({T}_{2}-{T}_{1}\right)
Sustituimos.
Q=\left(500\right)\left(0.212\right)\left(180-40\right)=14840 \mathrm{c}\mathrm{a}\mathrm{l}
Se deben suministrar 14840 calorías en forma de calor al bloque de aluminio para llevar su temperatura desde los 40°C a los 180°C. La respuesta correcta es el inciso c).
Reactivo 19
Una carga puntual q=-5\mathrm{n}\mathrm{C} se localiza en el origen. Obtener el vector del campo eléctrico en el punto del campo x=1 \mathrm{m} y y=-1.5 \mathrm{m} .
- (7.7\mathrm{N}/\mathrm{C})\widehat{i}-(11.54\mathrm{N}/\mathrm{C})\widehat{j}
- (-5.7\mathrm{N}/\mathrm{C})\widehat{i}+(9.54\mathrm{N}/\mathrm{C})\widehat{j}
- (-7.7\mathrm{N}/\mathrm{C})\widehat{i}+(11.54\mathrm{N}/\mathrm{C})\widehat{j}
- (5.7\mathrm{N}/\mathrm{C})\widehat{i}-(9.54\mathrm{N}/\mathrm{C})\widehat{j}
Solución:
El vector campo eléctrico se calcula aplicando la ley de Coulomb para el campo eléctrico.
\overrightarrow{E}=\frac{{k}_{e}q}{{\left|d\right|}^{2}}\overrightarrow{u}
Donde \overrightarrow{u} es un vector unitario en la dirección del campo eléctrico y \left|d\right| es el módulo del vector distancia entre la carga y el punto. Sustituimos al vector unitario \overrightarrow{u} como:
\overrightarrow{u}=\frac{\overrightarrow{d}}{\left|\overrightarrow{d}\right|}
La ecuación vectorial nos queda:
\overrightarrow{E}=\frac{{k}_{e}q}{{\left|d\right|}^{2}}\frac{\overrightarrow{d}}{\left|\overrightarrow{d}\right|}=\frac{{k}_{e}q}{{\left|d\right|}^{3}}\overrightarrow{d}
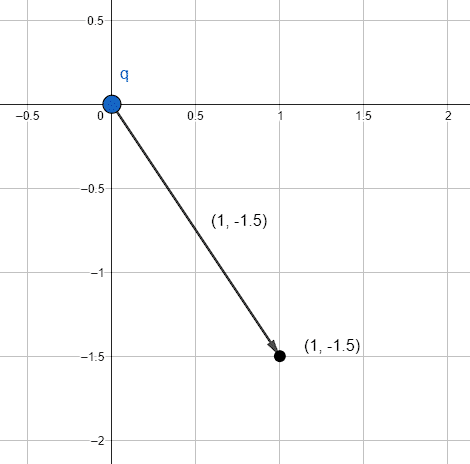
El vector distancia es:
\overrightarrow{d}=\left(1\widehat{i}-1.5\widehat{j}\right) \mathrm{m}
El módulo del vector distancia.
\left|d\right|=\sqrt{{1}^{2}+{\left(-1.5\right)}^{2}}=1.803 \mathrm{m}
Sustituimos a la carga de -5\mathrm{n}\mathrm{C}=-5\times {10}^{-9}\mathrm{C} , mientras que la constante dieléctrica es {k}_{e}=9\times {10}^{9}\frac{\mathrm{N}\cdot {\mathrm{m}}^{2}}{{\mathrm{C}}^{2}}\mathrm{ } .
\overrightarrow{E}=\frac{\left(9\times {10}^{9}\right)\left(-5\times {10}^{-9}\right)}{{\left(1.803\right)}^{3}}\left(1\widehat{i}-1.5\widehat{j}\right)
Simplificamos.
\overrightarrow{E}=\left(-7.68\right)\left(1\widehat{i}-1.5\widehat{j}\right)=\left(-7.7\widehat{i}+11.55\widehat{j}\right) \mathrm{N}/\mathrm{C}
El vector campo eléctrico en el punto x=1 \mathrm{m} y y=-1.5 \mathrm{m} es igual a \left(-7.7\widehat{i}+11.55\widehat{j}\right) \mathrm{N}/\mathrm{C} .
Escogemos como respuesta correcta al inciso c).
Reactivo 20
El flujo eléctrico es igual al producto de un elemento de ______ por la componente ____ del integrado de líneas del campo eléctrico sobre una superficie.
- área – paralela
- longitud – paralela
- área – perpendicular
- ancho – perpendicular
Solución:
La ley de Gauss establece que:
El flujo eléctrico que atraviesa una superficie cerrada, es igual a la suma de todas las contribuciones de los elementos de superficie d\overrightarrow{S} el producto escalar con el vector campo eléctrico perpendicular a la superficie en ese punto.
{\varphi }_{E}=\oint \overrightarrow{E}\cdot d\overrightarrow{s}
Teniendo en cuenta esto, el inciso que completa de forma correcta a la frase del enunciado es el c).
El flujo eléctrico es igual al producto de un elemento de área por la componente perpendicular del integrado de líneas del campo eléctrico sobre una superficie.


