Solución guiada de la tercera parte de la guía de física para el área de Ingeniería y Ciencias Físico Matemáticas, desde el reactivo 21 hasta el 30, como preparación al examen de ingreso al IPN.

Recuerda incluir exámenes simuladores durante tus períodos de estudio. Te permitirán acortar el tiempo que tardas al resolver los reactivos.
Reactivo 21
Cuatro capacitores están conectados como se muestra en la figura. Encontrar la capacitancia equivalente entre los puntos a y b.
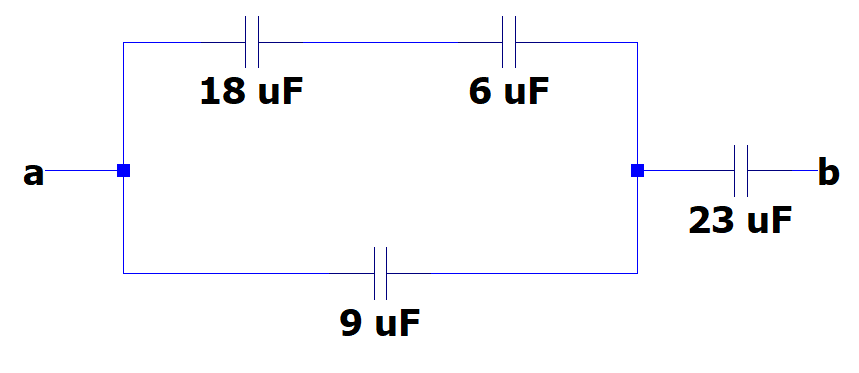
- 5.96\mu \mathrm{F}
- 8.5\mu \mathrm{F}
- 18.0\mu \mathrm{F}
- 44.1\mu \mathrm{F}
Solución:
Para calcular la capacitancia equivalente, debemos utilizar las ecuaciones para simplificar capacitores en serie y en paralelo.
Capacitores en paralelo.
{C}_{e}={C}_{1}+{C}_{2}
Capacitores en serie.
{C}_{e}=\frac{{C}_{1}{C}_{2}}{{C}_{1}+{C}_{2}}
Iniciamos resolviendo la serie entre los capacitores de 18 y 6 microfaradios.
{C}_{e1}=\frac{\left(18\right)\left(6\right)}{18+6}=4.5 \mathrm{u}\mathrm{F}
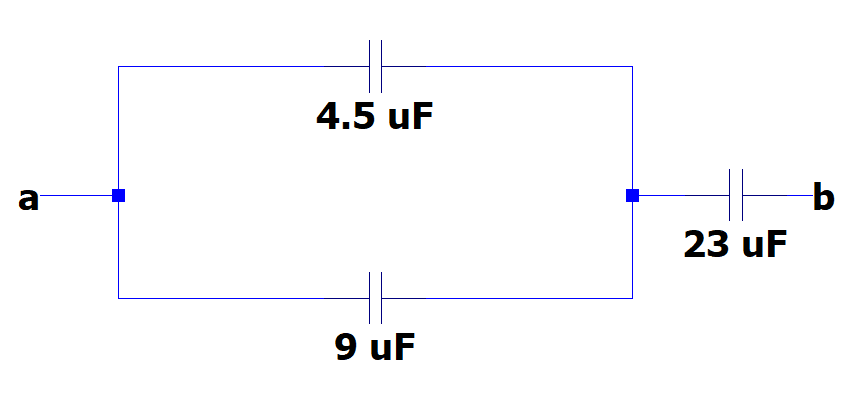
Resolvemos el paralelo.
{C}_{e2}=4.5 \mathrm{u}\mathrm{F}+9 \mathrm{u}\mathrm{F}=13.5\mathrm{ }\mathrm{u}\mathrm{F}

Finalmente, resolvemos la serie para encontrar la capacitancia equivalente entre a y b.
{C}_{e}=\frac{\left(13.5\right)\left(23\right)}{13.5+23}=8.5 \mathrm{u}\mathrm{F}
La capacitancia entre los terminales a y b es de 8.5 \mathrm{u}\mathrm{F} .
Indicamos como respuesta correcta al inciso b).
Reactivo 22
¿Cuál es la capacitancia equivalente de la combinación que se muestra en la figura?
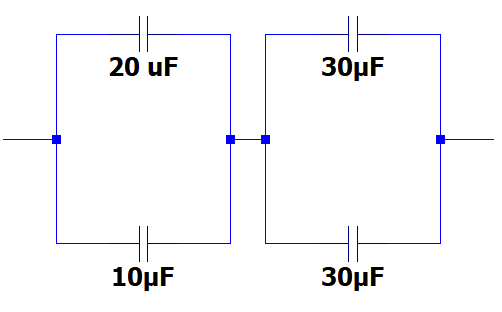
- 30\mu \mathrm{F}
- 20\mu \mathrm{F}
- 15\mu \mathrm{F}
- 10\mu \mathrm{F}
Solución:
Primero resolvemos los arreglos en paralelo del circuito.
{C}_{p1}=20+10=30 \mathrm{u}\mathrm{F}
{C}_{p2}=30+30=60 \mathrm{u}\mathrm{F}
El circuito nos quedaría:

El arreglo en paralelo quedaría:
{C}_{e}=\frac{\left(30\right)\left(60\right)}{30+60}=20 \mathrm{u}\mathrm{F}
La capacitancia equivalente del arreglo es igual a 20 microfaradios.
La respuesta correcta es el inciso b).
Reactivo 23
Un alambre de cobre cuyo diámetro es de 1 mm conduce una corriente constante de 1.5 A hacia una bombilla. En el alambre la densidad de electrones libres es de 8.46\times {10}^{28} electrones por {m}^{3} . ¿Cuál es la rapidez de arrastre?
- 0.6\times {10}^{-4}\frac{\mathrm{m}}{\mathrm{s}}
- 1.0\times {10}^{-4}\frac{\mathrm{m}}{\mathrm{s}}
- 1.4\times {10}^{-4}\frac{\mathrm{m}}{\mathrm{s}}
- 2.5\times {10}^{-4}\frac{\mathrm{m}}{\mathrm{s}}
Solución:
La rapidez de arrastre, es el módulo de la velocidad con la que se desplazan los electrones en un material conductor cuando se establece un campo eléctrico en su interior. La rapidez de arrastre se calcula a partir de la siguiente ecuación:
v=\frac{I}{e\cdot n \cdot S}
Donde I es la intensidad de corriente, e es la carga del electrón, n es la densidad electrónica y S el área de la sección transversal por la que circula la corriente. S se puede calcular a partir del diámetro del alambre.
S=\frac{\pi {D}^{2}}{4}=\frac{\pi {\left(0.001\right)}^{2}}{4}=7.854\times {10}^{-7} {\mathrm{m}}^{2}
La carga del electrón es igual a {q}_{e}=-1.602\times {10}^{-19} \mathrm{C} . Sustituimos los valores en la ecuación. La carga del electrón se sustituye sin el signo.
v=\frac{1.5}{\left(8.46\times {10}^{28}\right)\left(1.602\times {10}^{-19}\right)\left(7.854\times {10}^{-7}\right)}=1.41\times {10}^{-4} \mathrm{m}/\mathrm{s}
La rapidez de arrastre es igual a 1.41\times {10}^{-4} \mathrm{m}/\mathrm{s} .
La respuesta correcta es el inciso c).
Reactivo 24
El radio de un alambre de plata de 10 cm es de 0.2 mm. Calcular la resistencia de este, si la resistividad de la plata es de 1.59\times {10}^{-8}\mathrm{\Omega }\cdot \mathrm{m} .
- 0.0116\mathrm{\Omega }
- 0.0126\mathrm{\Omega }
- 0.0150\mathrm{\Omega }
- 0.0160\mathrm{\Omega }
Solución:
Para resolver el problema, utilizamos la ecuación de la resistencia eléctrica de un material.
R=\frac{\rho \cdot l}{A}
El área de la sección transversal se calcula como:
A=\pi {r}^{2}=\pi \left(0.0002\right)=1.26\times {10}^{-7} {\mathrm{m}}^{2}
Sustituimos todo en la ecuación de resistencia eléctrica.
R=\frac{\left(1.59\times {10}^{-8}\mathrm{\Omega }\cdot \mathrm{m}\right)\left(0.1 \mathrm{m}\right)}{1.26\times {10}^{-7} {\mathrm{m}}^{2}}=0.0126 \mathrm{\Omega }
La respuesta correcta es el inciso b).
Reactivo 25
¿Cómo se define la conductividad de un material?
- \sigma =\frac{1}{F}
- \sigma =\frac{1}{E}
- \sigma =\frac{1}{\rho }
- \sigma =\frac{1}{R}
Solución:
La conductividad de un material es la facilidad que este tiene para permitir el flujo de corriente a través de él. La conductividad es inversamente proporcional a la resistividad \rho .
\sigma =\frac{1}{\rho }
La respuesta correcta es el inciso c).
Reactivo 26
Ordenar en forma ascendente y de acuerdo con la Ley de Ohm el valor de las siguientes resistencias:
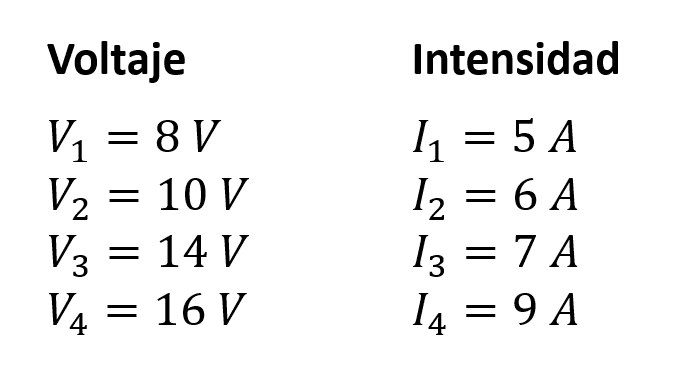
- {R}_{1},{R}_{2},{R}_{4},{R}_{3}
- {R}_{2},{R}_{1},{R}_{3},{R}_{4}
- {R}_{1},{R}_{4},{R}_{2},{R}_{3}
- {R}_{2},{R}_{3},{R}_{4},{R}_{1}
Solución:
Para calcular la resistencia eléctrica en cada caso, empleamos la Ley de Ohm.
R=\frac{V}{I}
Primera resistencia.
{R}_{1}=\frac{8}{5}=1.6 \mathrm{\Omega }
Segunda resistencia.
{R}_{2}=\frac{10}{6}=1.66 \mathrm{\Omega }
Tercera resistencia.
{R}_{3}=\frac{14}{7}=2 \mathrm{\Omega }
Cuarta resistencia.
{R}_{4}=\frac{16}{9}=1.77 \mathrm{\Omega }
Ordenadas de menor a mayor, las resistencias quedarían:
{R}_{1}, {R}_{2}, {R}_{4}, {R}_{3}
La respuesta correcta es el inciso a).
Reactivo 27
Una batería tiene una fem de 1.5 V. El potencial en sus terminales cae a cero cuando una corriente de 2.4 A pasa a través de ella. ¿Cuál es su resistencia interna?
- 0.725\mathrm{\Omega }
- 0.625\mathrm{\Omega }
- 0.590\mathrm{\Omega }
- 0.525\mathrm{\Omega }
Solución:
En la realidad, tanto las fuentes de alimentación como los instrumentos de medición tienen asociada una resistencia equivalente en serie o paralelo que permite modelar las pérdidas de potencia, consumo de corriente y caída de tensión que se produce en ellos.
Teniendo eso en cuenta, una batería puede dibujarse de la siguiente forma:
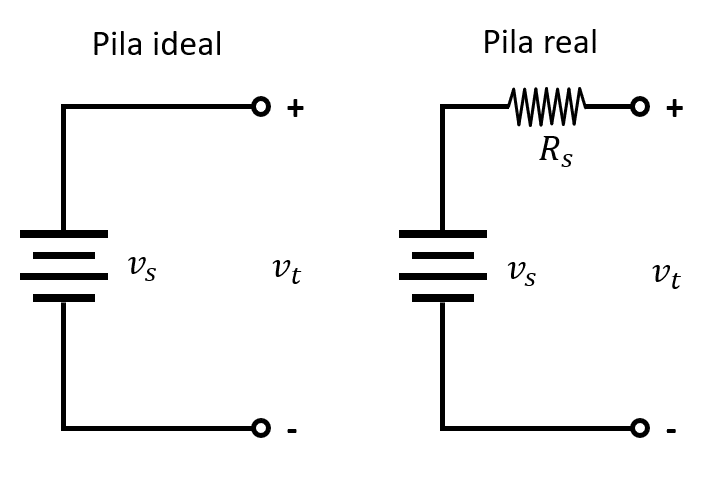
Ahora, esta resistencia en serie provoca una pequeña caída de tensión que depende de la corriente suministrada por la fuente. Cuando la tensión en terminales de la batería real se lleva la tensión a cero, significa que los terminales han sido cortocircuitados.
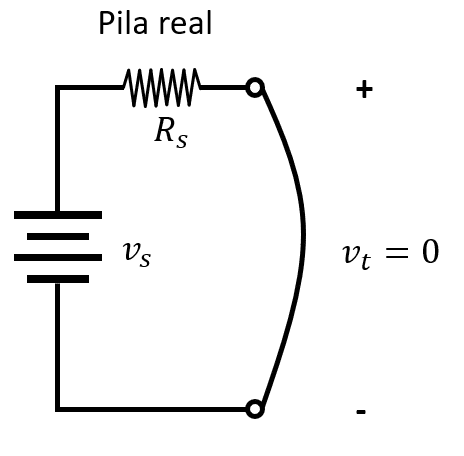
Si aplicamos la ley de Mallas para circuitos eléctricos nos queda:
{v}_{s}-{v}_{R}=0\to {v}_{R}={v}_{s}
La tensión de la resistencia en serie es igual a la FEM de la pila. Debido a que la corriente de 2.4 A circula por la resistencia serie, podemos calcular su valor mediante la ley de Ohm.
{R}_{s}=\frac{{v}_{s}}{{i}_{s}}=\frac{1.5 \mathrm{V}}{2.4 \mathrm{A}}=0.625 \mathrm{\Omega }
La resistencia interna de la pila es de 0.625 \mathrm{\Omega } .
La respuesta correcta es el inciso b).
Reactivo 28
Un motor eléctrico consume 5 A de una línea de 120 V. Determinar la potencia aportada y la energía suministrada al motor en 1h.
- 5 kW y 2.16 MJ
- 6 kW y 2.16 MJ
- 6 kW y 2.45 MJ
- 5kW y 2.45 MJ
Solución:
La potencia eléctrica en corriente continua se calcula como:
P=V\cdot I
Sustituimos los valores dados por el enunciado.
P=\left(5\right)\left(120\right)=600 \mathrm{W}
Expresado en kiloWatts.
P=0.6 \mathrm{k}\mathrm{W}
La potencia es igual a la energía suministrada por unidad de tiempo \left[\frac{\mathrm{J}}{\mathrm{s}}\right] . Podemos obtener la energía suministrada al motor multiplicando los 3600 segundos por la potencia.
E=P\cdot \mathrm{\Delta }t=\left(600\right)\left(3600\right)=2160000 \mathrm{J}
Expresado en mega Joules nos queda:
E=2.16 \mathrm{M}\mathrm{J}
Comparando nuestros resultados con los incisos, concluimos que la respuesta correcta es el b).
Reactivo 29
Un motor de 120 V consume una corriente de 4.0 A. ¿Cuántos Joules de energía eléctrica utiliza en 1h?
- 73 MJ
- 49 kJ
- 49 MJ
- 73kJ
Solución:
La energía eléctrica suministrada al motor eléctrico durante 1 hora se calcula como.
E=V\cdot I\cdot \mathrm{\Delta }t
El tiempo se sustituye en segundos.
E=\left(120\right)\left(4\right)\left(3600\right)=1728000 \mathrm{J}
Expresado en Mega Joules.
E=1.728 \mathrm{M}\mathrm{J}
La respuesta correcta es el inciso a).
Reactivo 30
Una celda electroquímica se forma con dos conductores llamados electrodos que están sumergidos en una solución _______ cuya finalidad es producir electricidad mediante una reacción redox espontánea. Se considera que es una celda electroquímica _________ si la reacción no es reversible.
- concentrada – secundaria
- electrolítica – secundaria
- electrolítica – primaria
- diluida – primaria
Solución:
Las celdas electroquímicas son dispositivos que permiten convertir energía química producida por reacciones espontáneas en energía eléctrica. Dichas reacciones químicas se conocen como redox.
Por otra parte, las celdas electroquímicas se dividen en dos tipos: galvánicas y electrolíticas. Las galvánicas se utilizan para producir energía eléctrica mientras que las electrolíticas permiten forzar reacciones de oxidoreducción que no ocurren de forma espontánea.
Las celdas galvánicas se subdividen en: primarias y secundarias. En las primarias, la energía química se convierte en eléctrica de forma irreversible.
Mientras que, en las secundarias, el flujo de energía puede ser revertido. Un ejemplo de celdas galvánicas secundarias, son las pilas recargables.
Con toda esta información y examinando los incisos, podemos concluir que las palabras que completan al enunciado son: electrolítica y primaria.
Una celda electroquímica se forma con dos conductores llamados electrodos que están sumergidos en una solución electrolítica cuya finalidad es producir electricidad mediante una reacción redox espontánea. Se considera que es una celda electroquímica primaria si la reacción no es reversible.
Concluimos que la respuesta correcta es el inciso c).

