Con este post iniciamos la solución de los primeros 30 reactivos del simulador de Matemáticas del examen IPN para el área Ciencias Sociales y Administrativas del Instituto Politécnico Nacional.

Antes de checar la solución, resuelve los ejercicios por tu cuenta.
Temario Matemáticas Cs Sociales y Administrativas
Te dejo una lista con todos los temas de matemáticas que deberás estudiar para presentar el examen de ingreso:
- Razonamiento matemático.
- Algebra.
- Geometría y trigonometría.
- Geometría analítica.
- Probabilidad y estadística.
- Cálculo diferencial
- Cálculo integral.
¿Cómo resolver el simulacro?
Estos problemas han sido diseñados para que puedas practicar los temas del examen real y mejorar el tiempo que tardas en resolverlos.
Incluye exámenes simulacro en tu rutina de estudio, de esa forma pondrás a prueba tus conocimientos en condiciones similares a la prueba real. Las siguientes son sugerencias para tener en cuenta mientras estudias con este examen simulacro.
- Resuelve cada parte (I, II y III) por tu cuenta antes de checar las respuestas.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
- Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo.
- Asegúrate de tener unos minutos de sobra para comprobar tus respuestas.
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico.
Reactivo 1
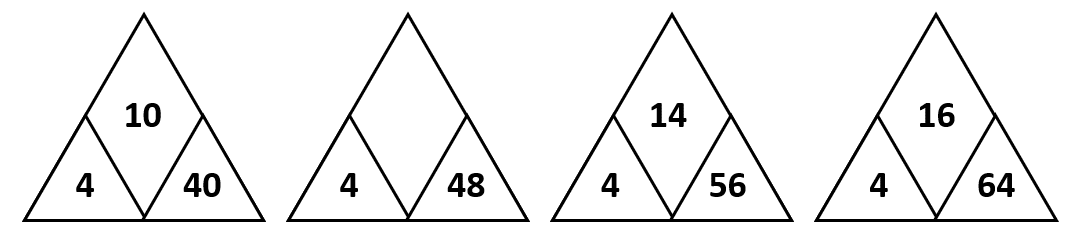
Indique el número que falta en el espacio vacío de las siguientes figuras.
- 11
- 12
- 13
- 15
Solución:
Para rellenar correctamente el espacio en blanco, primero debemos identificar la relación entre los números. En la primera figura, obtenemos al 40 multiplicando 4 por 10. Lo mismo pasa con la tercera y cuarta figura:
4\times 14=56
4\times 16=64
Otra relación que podemos identificar, es que los números en la parte superior de los triángulos incrementan en pasos de 2. Por tanto, el número en la casilla vacía es 12, debemos comprobar multiplicando 4 por 12.
4\times 12=48
Finalizamos seleccionando al inciso b) como respuesta correcta.
Reactivo 2
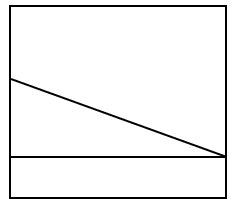
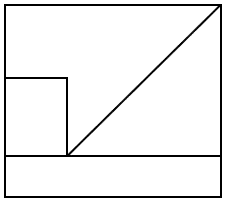
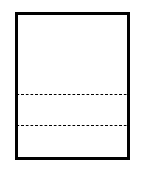
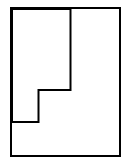
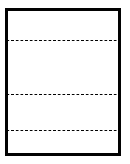
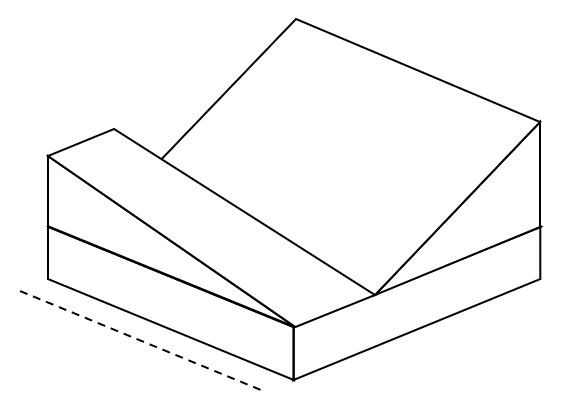
Identificar la imagen que corresponde a la vista frontal de la siguiente figura. Tenga en cuenta que la vista solicitada se marca con una línea discontinua.
Solución:
Para resolver este ejercicio debemos emplear la memoria espacial, de tal forma que proyectemos en una superficie plana la vista solicitada. Comencemos proyectando la base de la figura tridimensional, la cuál sería un rectángulo en la parte inferior.
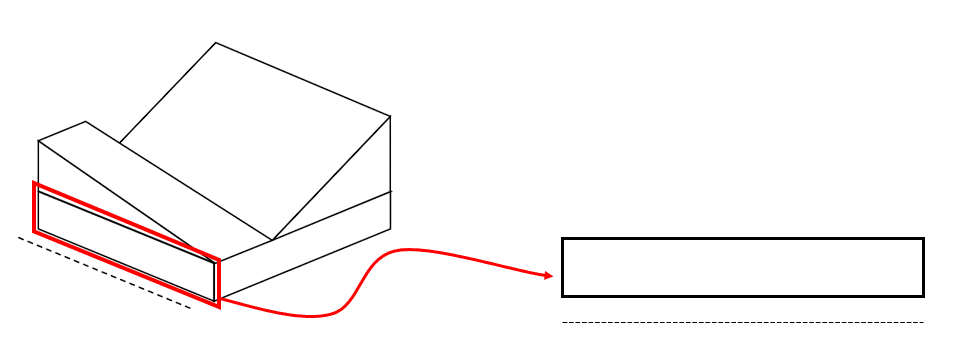
Ahora vamos con la rampa delantera. Esta se vería como un triángulo rectángulo acostado sobre la base.
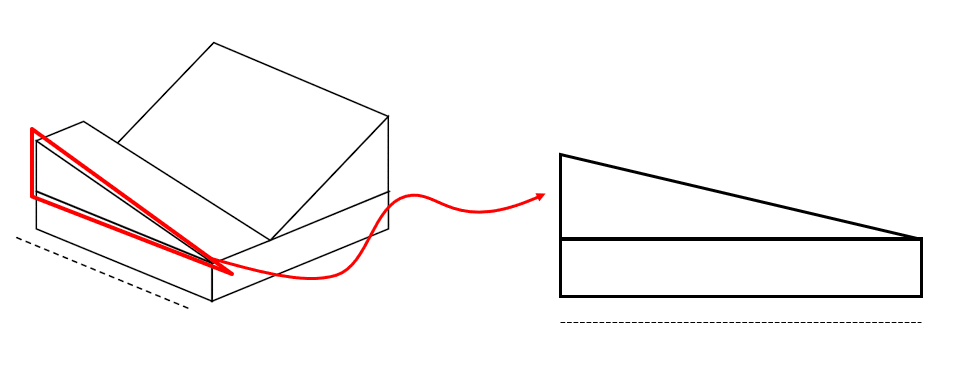
Finalmente, la rampa del fondo se vería como un rectángulo tapado por el triángulo anterior.
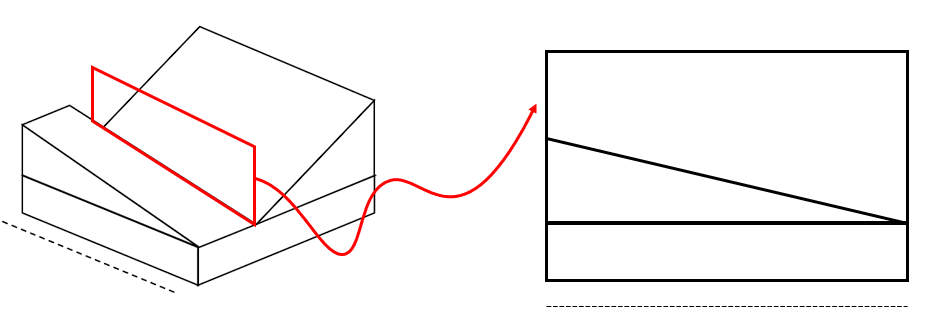
Comparando nuestro resultado con los incisos, concluimos que la respuesta correcta es el a).
Reactivo 3
Identificar la figura que completa adecuadamente la siguiente secuencia gráfica.
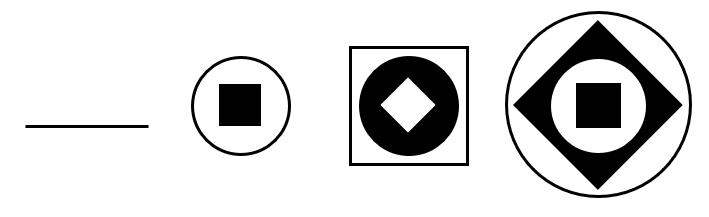
Solución:
El procedimiento para resolver series gráficas consta en analizar la forma en que cambian y aparecen en las figuras los elementos gráficos. Lo primero que podemos ver, es que en el centro de todos los términos la figura cambia entre cuadrado negro y rombo blanco.
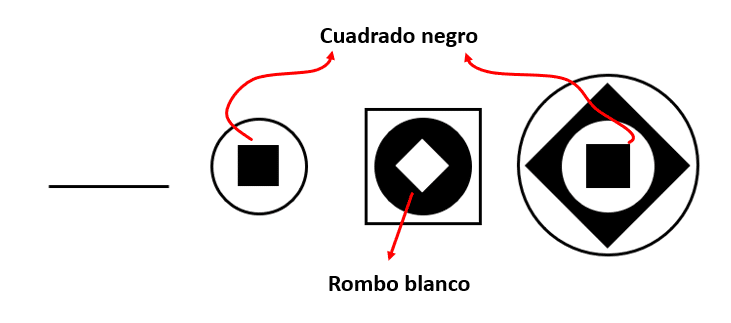
En el término restante debe encontrarse un rombo blanco.
¿Debería tener algo que lo rodee? Si examinamos la serie, veremos como el resto de figuras se agregan como capas alrededor del cuadrado y del robo. Además, la circunferencia es el nivel más bajo en esas capas. Concluimos entonces que el término faltante solo debe tener un rombo blanco.
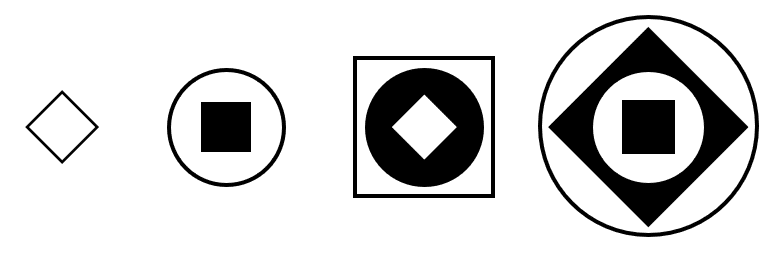
La respuesta correcta es el inciso b).
Reactivo 4
Identificar la figura que corresponde al cuadrado vacío.
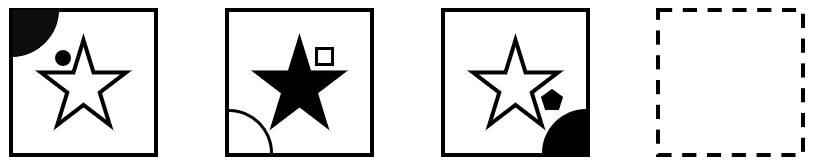
Solución:
En los términos de la serie gráfica podemos identificar 3 elementos: una estrella, una figura entre las aristas de la estrella y un cuarto de sección circular. Comencemos analizando a la estrella.
Cambia de relleno entre blanco y negro.
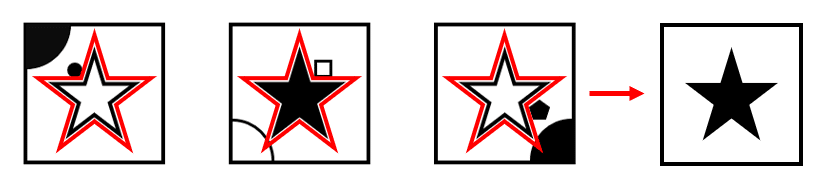
El sector circular varía de dos formas: cambia de esquina en sentido contrario a las agujas del reloj y alterna su color de relleno. Para el término faltante, debería ser blanca y situarse en la equina superior derecha.
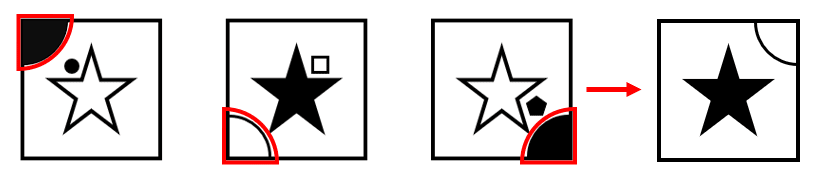
La figura entre las aristas de la estrella alterna su color, gira en sentido de las agujas del reloj y agrega una arista en cada término. En base a esto, la siguiente deberá ser un hexágono blanco y situarse en la parte inferior.

La respuesta correcta es el inciso c).
Reactivo 5
Relacionar las expresiones con el área que les corresponde, basándose en la siguiente figura.
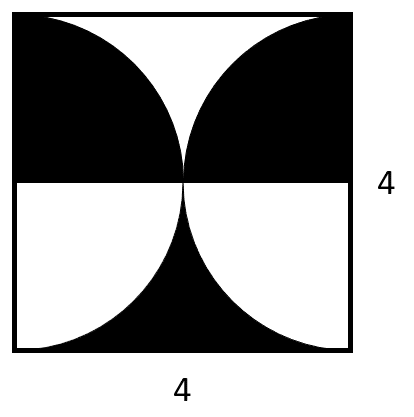

- 1A, 2B, 3C, 4D
- 1B, 2C, 3D, 4A
- 1B, 2A, 3C, 4D
- 1C, 2D, 3A, 4B
Solución:
Para resolver este problema, iremos calculando el área solicitada en los incisos de la columna izquierda para luego relacionarlo con la expresión en la columna derecha.
Área total de las zonas sombreadas.
Es decir, el área de las regiones en color negro. Si reflejamos los sectores circulares negros de la parte superior hacia la parte inferior nos queda:
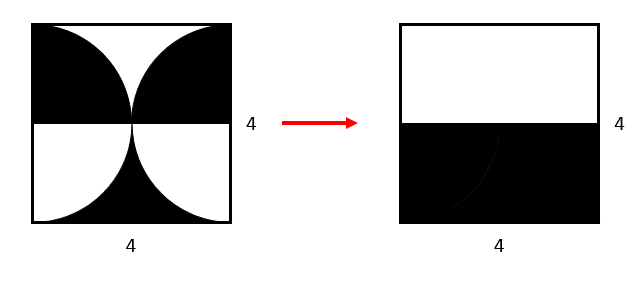
Por tanto, la zona sombreada total es la mitad del área del cuadrado.
{A}_{a}=\frac{4\cdot 4}{2}=8 {\mathrm{u}}^{2}
Comparando con la columna derecha: 1B.
Área de la zona inferior sombreada.
Es el área de la mitad del cuadrado menos el área de dos cuartos de circulo de radio 2.
{A}_{b}=8-2\cdot \frac{\pi {r}_{b}^{2}}{4}=8-\frac{\pi {\left(2\right)}^{2}}{2}=8-2\pi {\mathrm{u}}^{2}
\therefore {A}_{b}=8-2\pi {\mathrm{u}}^{2}
Comparando con la columna derecha: 2A.
Área de la zona superior sombreada.
Es equivalente al área de dos cuartos de circulo de radio 2.
{A}_{c}=2\cdot \frac{\pi {r}_{c}^{2}}{4}=\frac{\pi {\left(2\right)}^{2}}{2}=2\pi {\mathrm{u}}^{2}
Comparando con la columna derecha: 3C. Por descartes, el inciso 4 queda pareado con el inciso D. Uniendo todas las soluciones:
1B, 2A, 3C, 4D.
Concluimos que la respuesta correcta es la opción c).
Reactivo 6
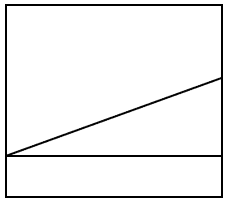
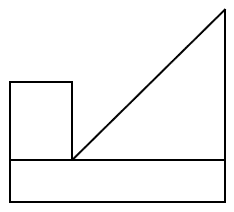
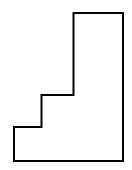
Indicar la respuesta que corresponde a la vista de perfil de la figura tridimensional.
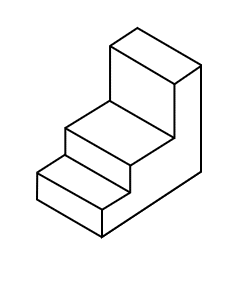
Solución:
Este problema es sencillo, pero debemos tener en cuenta un detalle bastante importante. En dibujo técnico, los cuerpos en tres dimensiones pueden descomponerse en 3 vistas: alzada, de perfil y de planta.
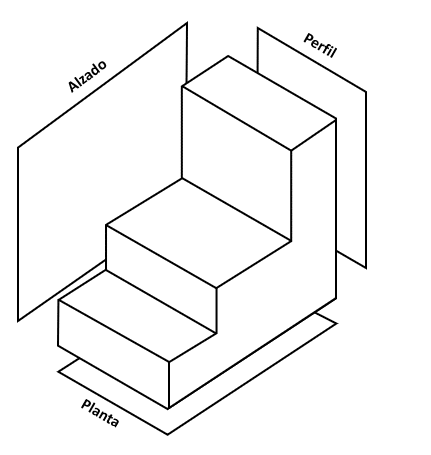
La vista de perfil es la que obtenemos al observar al objeto de forma frontal. En dicho caso, la vista de perfil (frontal) sería un rectángulo alargado con dos rectas paralelas a la base que representan a los escalones de la figura.
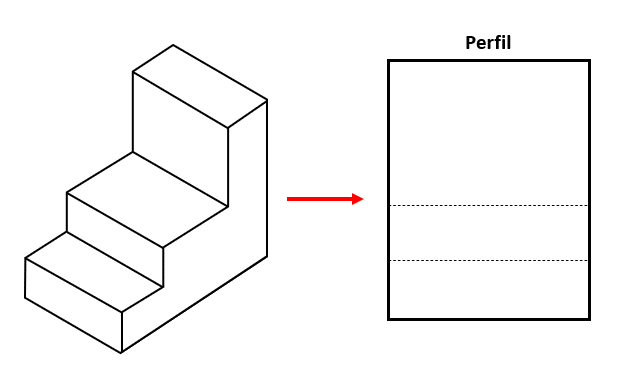
La respuesta correcta es el inciso a).
Reactivo 7
Una empresa constructora debe calcular los viáticos a pagar al grupo de albañiles que construyen un muro de 12 metros de ancho por 5 metros de alto. Gracias a la data que guardan los arquitectos, se sabe que 10 albañiles construyeron un muro de 20 metros cuadrados en 7 días. Si el cobro por día de cada albañil es de 200$, ¿cuánto dinero debe destinar la constructora por albañil en mano de obra, para el muro de 12 por 5 metros con 10 albañiles?
- 1200$
- 42000$
- 12000$
- 4200$
Solución:
En este problema, debemos utilizar la regla de tres compuesta para encontrar los días que tardarían los 10 albañiles en construir el muro, para luego calcular el cobro de cada uno. El muro a construir tiene un área de 12 \mathrm{m}\times 5 \mathrm{m}=60 {\mathrm{m}}^{2} . La regla de tres compuesta quedaría:

Debido a que el número de albañiles es igual, podemos simplificar de regla de tres compuesta a regla de tres simple.

Ahora, ¿la relación es directa o inversa? A mayor superficie, mayor será el tiempo de construcción y, por ende, más días se tardará el grupo de albañiles. Relación directa.
\frac{x}{7}=\frac{60}{20}\to x=7\left(3\right)=21
Los 10 albañiles se tardarían 21 días en construir el muro. Si cada albañil cobra 200$ el día, por 21 días el cobro por el proyecto será 4200$. Concluimos indicando como correcta la opción d).
Reactivo 8
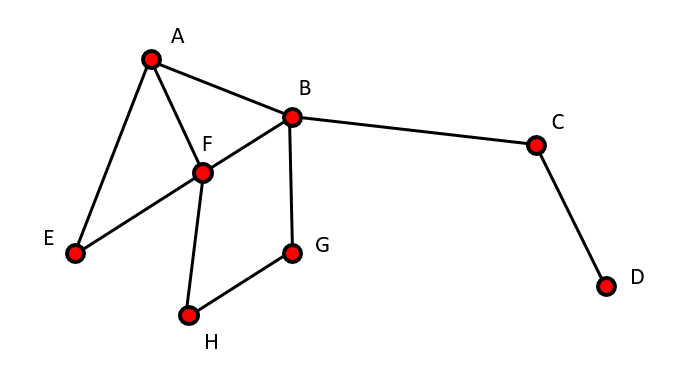
Completar la siguiente secuencia con base en la figura que se muestra.
____, \left(4, \mathrm{B}\right), \left(2, \mathrm{C}\right), \left(1, \mathrm{D}\right), \left(2, \mathrm{E}\right), \dots .
- \left(2, \mathrm{A}\right)
- \left(1, \mathrm{A}\right)
- \left(4, \mathrm{A}\right)
- \left(3, \mathrm{A}\right)
Solución:
En la figura se muestra un grafo, objeto de las matemáticas discretas muy poderoso en áreas como la física, la química, la biología y la teoría de la informática. En la parte superior, se muestran duplas compuestas por un número y una letra, correspondiente a los vértices del grafo.
Examinando a la figura, nos daremos cuenta que el número corresponde a la cantidad de conexiones que posee el vértice. El B tiene 4 conexiones, el C tiene 2, el D una conexión y así sucesivamente.
En esta línea de idead, la dupla que falta debería contener al vértice A el cuál posee 3 conexiones.
\left(3, A\right)
La serie completa quedaría:
\left(3, A\right), \left(4, \mathrm{B}\right), \left(2, \mathrm{C}\right), \left(1, \mathrm{D}\right), \left(2, \mathrm{E}\right), \dots
Concluimos entonces que la respuesta correcta es el inciso d).
Reactivo 9
El encargado de un almacén necesita apilar las cajas desordenadas, de tal forma que las ligeras quedan arriba y las pesadas abajo. El peso de las cajas depende de su contenido, a continuación, se muestra un gráfico ilustrativo de las cajas.
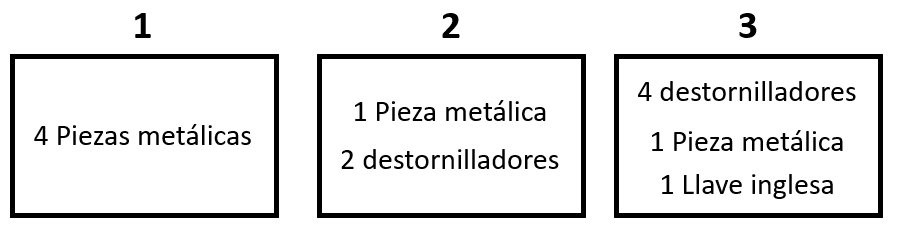
Pieza metálica: 1 kg, Destornilladores: 0.5 kg y Llave inglesa 1.2 kg.
- 1, 2, 3
- 2, 1, 3
- 3, 1, 2
- 2, 3, 1
Solución:
Comencemos por calcular el peso de cada caja. Caja1.
{P}_{1}=4\cdot PM=4\cdot \left(1 \mathrm{k}\mathrm{g}\right)=4 \mathrm{k}\mathrm{g}
Peso de la caja 2.
{P}_{2}=PM+2D=1 \mathrm{k}\mathrm{g}+2\left(0.5 \mathrm{k}\mathrm{g}\right)=2 \mathrm{k}\mathrm{g}
Peso de la caja 3.
{P}_{3}=4D+PM+LLI=4\left(0.5 \mathrm{k}\mathrm{g}\right)+1 \mathrm{k}\mathrm{g}+1.2\mathrm{ }\mathrm{k}\mathrm{g}=4.2\mathrm{ }\mathrm{k}\mathrm{g}
Ordenadas desde la más ligera a la más pesada quedarían:
Caja 2 – Caja 1 – Caja 3.
Concluimos que la respuesta correcta es el inciso b).
Reactivo 10
Calcular el valor de x a partir de la siguiente expresión.
-5{x}^{2}+{\left(x-1\right)}^{2}+3=3-4{x}^{2}
- x=1
- x=-1
- x=\frac{1}{2}
- x=-\frac{1}{2}
Solución:
Antes de agrupar términos, comencemos por desarrollar el producto notable.
-5{x}^{2}+{x}^{2}-2x+1+3=3-4{x}^{2}
Agrupando las x al miembro de la derecha nos queda:
-5{x}^{2}+4{x}^{2}+{x}^{2}-2x=3-3-1
-5{x}^{2}+5{x}^{2}-2x=-1
-2x=-1
Finalmente:
x=\frac{1}{2}
La respuesta correcta es el inciso c).
Reactivo 11
Simplifica la siguiente expresión algebraica.
{\left(\frac{{x}^{2}-4x+3}{x-3}\right)}^{2}
- {x}^{2}+1
- 1-2x
- {\left(x-3\right)}^{2}
- {x}^{2}-2x+1
Solución:
Ignoremos por un momento el exponente de la fracción y pasemos a intentar factorizar el polinomio de segundo grado.
{x}^{2}-4x+3=\left(x+a\right)\left(x+b\right)
Buscamos a dos números a y b que multiplicados den 3 y sumados den -4. Estos son -3 y -1.
{x}^{2}-4x+3=\left(x-3\right)\left(x-1\right)
Sustituimos en la fracción:
{\left[\frac{\left(x-3\right)\left(x-1\right)}{x-3}\right]}^{2}
Simplificamos.
{\left[\frac{\left(x-3\right)\left(x-1\right)}{x-3}\right]}^{2}={\left(x-1\right)}^{2}
Debido a que en los incisos no se encuentra este resultado, pasemos a desarrollar el producto notable.
{\left(x-1\right)}^{2}={x}^{2}-2x+1
Finalmente:
{\left(\frac{{x}^{2}-4x+3}{x-3}\right)}^{2}={x}^{2}-2x+1
La respuesta correcta es el inciso d).
Reactivo 12
Indique el número que cumple con la siguiente descripción:
El tercio de un número más 4 y la suma multiplicada por 3 es igual a 15.
- -3
- 3
- 4
- 1
solución:
Primero, expresemos la frase en lenguaje natural a lenguaje algebraico.
El tercio de un número más 4 y la suma multiplicada por 3 es igual a 15.
3\left(\frac{x}{3}+4\right)=15
Despejamos a x .
x+12=15\to x=3
El número que cumple la condición es 3.
La respuesta correcta es b).
Reactivo 13
Encuentra la forma factorizada de la siguiente expresión.
{x}^{2n}-{y}^{2m}
- \left({x}^{n}+{y}^{m}\right)\left({x}^{n}-{y}^{m}\right)
- \left({x}^{n}+{y}^{m}\right)
- \left({x}^{n}-{y}^{m}\right)
- \left({x}^{2n}+{y}^{n}\right)\left({x}^{2n}-{y}^{n}\right)
Solución:
Para resolver este problema, debemos emplear el producto notable de la diferencia de cuadrados.
{a}^{2}-{b}^{2}=\left(a-b\right)\left(a+b\right)
Si expresamos a las potencias como potencia de una potencia nos queda algo similar a lo anterior.
{\left({x}^{n}\right)}^{2}-{\left({y}^{m}\right)}^{2}=\left({x}^{n}-{y}^{m}\right)\left({x}^{n}+{y}^{m}\right)
Comparando con los incisos, la respuesta correcta es el a).
Reactivo 14
Resuelve el siguiente sistema de ecuaciones lineales.
\left\{\begin{array}{c}x+y+z=1\\ 2x-y+z=2\\ x-2y-z=4\end{array}\right.
- \begin{array}{c}x=-3\\ z=-3\\ y=1\end{array}
- \begin{array}{c}x=3\\ z=-3\\ y=1\end{array}
- \begin{array}{c}x=-3\\ z=3\\ y=1\end{array}
- \begin{array}{c}x=-3\\ z=-3\\ y=-1\end{array}
Solución:
Debido a que se trata de un sistema de tres ecuaciones con tres incógnitas, tenemos dos opciones: aplicar el método por reducción o la regla de Cramer. Para evitar sustituciones progresivas y posibles errores en el proceso, aplicaremos la regla de Cramer. Comenzamos construyendo los determinantes.
Determinante del sistema.
{\mathrm{\Delta }}_{s}=\left|\begin{array}{ccc}1& 1& 1\\ 2& -1& 1\\ 1& -2& -1\end{array}\right|=\left|\begin{array}{cc}-1& 1\\ -2& -1\end{array}\right|\left(1\right)-\left|\begin{array}{cc}2& 1\\ 1& -1\end{array}\right|\left(1\right)+\left|\begin{array}{cc}2& -1\\ 1& -2\end{array}\right|\left(1\right)
Resolvemos los determinantes indicados.
{\mathrm{\Delta }}_{s}=\left(1+2\right)\left(1\right)-\left(-2-1\right)\left(1\right)+\left(-4+1\right)\left(1\right)=3+3-3=3
{\mathrm{\Delta }}_{s}=3
Determinante de x .
{\mathrm{\Delta }}_{x}=\left|\begin{array}{ccc}1& 1& 1\\ 2& -1& 1\\ 4& -2& -1\end{array}\right|=\left|\begin{array}{cc}-1& 1\\ -2& -1\end{array}\right|\left(1\right)-\left|\begin{array}{cc}2& 1\\ 4& -1\end{array}\right|\left(1\right)+\left|\begin{array}{cc}2& -1\\ 4& -2\end{array}\right|\left(1\right)
{\mathrm{\Delta }}_{x}=\left(1+2\right)\left(1\right)-\left(-2-4\right)\left(1\right)+\left(-4+4\right)\left(1\right)=9
x=\frac{{\mathrm{\Delta }}_{x}}{{\mathrm{\Delta }}_{s}}=\frac{9}{3}=3
Determinante de y .
{\mathrm{\Delta }}_{y}=\left|\begin{array}{ccc}1& 1& 1\\ 2& 2& 1\\ 1& 4& -1\end{array}\right|=\left|\begin{array}{cc}2& 1\\ 4& -1\end{array}\right|\left(1\right)-\left|\begin{array}{cc}2& 1\\ 1& -1\end{array}\right|\left(1\right)+\left|\begin{array}{cc}2& 2\\ 1& 4\end{array}\right|\left(1\right)
{\mathrm{\Delta }}_{y}=\left(-2-4\right)\left(1\right)-\left(-2-1\right)\left(1\right)+\left(8-2\right)\left(1\right)=3
y=\frac{{\mathrm{\Delta }}_{y}}{{\mathrm{\Delta }}_{s}}=\frac{3}{3}=1
Para el valor de z , sustituimos a x y y en cualquiera de las ecuaciones. Escogemos a la primera.
x+y+z=1\to z=1-x-y
z=1-3-1=-3
El punto que satisface el sistema de ecuaciones es:
\left(3, 1, -3\right)
La respuesta correcta es el inciso b).
Reactivo 15
Desarrolla el siguiente producto notable.
{\left(\frac{1}{x}-y\right)}^{2}
- \frac{1}{{x}^{2}}-\frac{2y}{x}+{y}^{2}
- \frac{1}{{x}^{2}}+\frac{2y}{x}+{y}^{2}
- \frac{1}{{x}^{2}}-\frac{2y}{x}-{y}^{2}
- \frac{1}{{x}^{2}}-\frac{2y}{x}+y
Solución:
Para desarrollar el binomio al cuadrado, empleamos el producto notable con el mismo nombre.
{\left(a-b\right)}^{2}={a}^{2}-2ab+{b}^{2}
Aplicando a la expresión del enunciado:
{\left(\frac{1}{x}\right)}^{2}-2\left(\frac{1}{x}\right)\left(y\right)+{y}^{2}=\frac{1}{{x}^{2}}-\frac{2y}{x}+{y}^{2}
Finalmente:
{\left(\frac{1}{x}-y\right)}^{2}=\frac{1}{{x}^{2}}-\frac{2y}{x}+{y}^{2}
La respuesta correcta es el inciso a).
Reactivo 16
¿Cuál de las siguientes opciones describe la siguiente expresión algebraica?
\mathrm{ln}\frac{x}{y}=\mathrm{ln}x-\mathrm{ln}y
- El logaritmo del cociente de dos números es igual al logaritmo de la diferencia
- El logaritmo del cociente de dos números es igual a la diferencia de los números
- El logaritmo del producto es igual a la suma de los logaritmos
- El logaritmo del cociente de dos números es igual a la diferencia de los logaritmos
Solución:
Para expresar a la operación en lenguaje natural, debemos describir a cada uno de los elementos que participan en ella.
\mathrm{ln}\frac{x}{y}
El logaritmo del cociente de dos números. Cuando decimos dos números, se alude a x y y .
\mathrm{ln}x-\mathrm{ln}y
La diferencia de los logaritmos de dos números. Uniendo ambas frases nos queda:
El logaritmo del cociente de dos números, es igual a la diferencia de sus logaritmos.
Examinando las frases en los incisos, la única que describe correctamente lo anterior es el d).
\mathrm{ln}\frac{x}{y}=\mathrm{ln}x-\mathrm{ln}y
El logaritmo del cociente de dos números es igual a la diferencia de los logaritmos
Reactivo 17
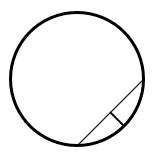
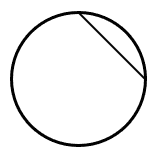
¿Cuál de las siguientes figuras representa la sagita de la circunferencia?
Solución:
¿Qué es la sagita? También conocida como flecha, es un segmento de recta que se traza desde una cuerda hasta el centro de un sector circular. Teniendo en cuenta que los extremos de la cuerda son los extremos del sector circular.
Entre los incisos, los únicos que muestran circunferencia con cuerdas dentro de ellas son el c y el d.
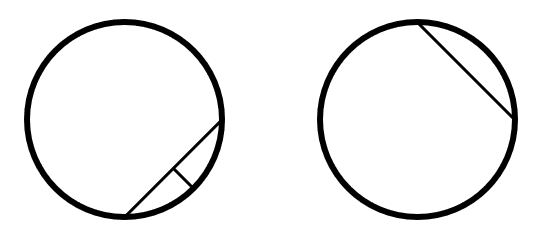
De estas dos, la única que muestra un segmento entre la cuerda y el sector circular es el c).
La respuesta correcta es el inciso c).
Reactivo 18
La función trigonométrica \mathrm{tan}x es equivalente a:
- \sqrt{1+{\mathrm{sin}}^{2}x}
- \sqrt{1+{\mathrm{cos}}^{2}x}
- \sqrt{1+{\mathrm{sec}}^{2}x}
- \sqrt{{\mathrm{sec}}^{2}x-1}
Solución:
Debido a que los incisos muestran razones trigonométricas con raíces cuadradas y elevadas al cuadrado, podemos asociar la solución con la identidad pitagórica en términos de la tangente.
{\mathrm{tan}}^{2}x+1={\mathrm{sec}}^{2}x
Despejando a la tangente nos queda:
{\mathrm{tan}}^{2}x={\mathrm{sec}}^{2}x-1\to \mathrm{tan}x=\pm \sqrt{{\mathrm{sec}}^{2}x-1}
Seleccionando la parte positiva.
\mathrm{tan}x=\sqrt{{\mathrm{sec}}^{2}x-1}
La respuesta correcta es el inciso d).
Reactivo 19
Si \mathrm{tan}\alpha =\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{d}\mathrm{o} , ¿cuál es el valor de \mathrm{cos}\alpha ?
- 0
- 1
- -1
- Indeterminado
Solución:
Cuando decimos que una función se indetermina, es porque la misma toma un valor infinitamente grande +\infty o infinitamente pequeño -\infty . En este caso, la tangente puede escribirse como:
\mathrm{tan}x=\frac{\mathrm{sin}x}{\mathrm{cos}x}
Un cociente se indetermina cuando el denominador se anula, es decir, cuando \mathrm{cos}x=0 . Para efectos del enunciado, \mathrm{cos}\alpha =0 . La respuesta correcta es el inciso a).
Respuesta correcta: a).
Reactivo 20
Relacione los polígonos indicados en la columna izquierda con los ángulos internos entre dos aristas consecutivas que se indican en la columna derecha.

- 1C, 2B, 3D, 4A
- 1B, 2C, 3D, 4A
- 1C, 2D, 3B, 4A
- 1A, 2B, 3C, 4D
Solución:
Para relacionar correctamente ambas columnas, debemos recordar una ecuación básica de los polígonos regulares:
\theta =\frac{180\left(n-2\right)}{n}
Donde \theta es la magnitud de los ángulos internos del polígono y n el número de lados.
Ángulos de un rectángulo.
{\theta }_{1}=\frac{180\left(4-2\right)}{4}=90°
1C.
Ángulos de un Hexágono.
{\theta }_{2}=\frac{180\left(6-2\right)}{6}=120°
2B.
Ángulos de un Pentágono.
{\theta }_{3}=\frac{180\left(5-2\right)}{5}=108°
3D.
Por descarte, el inciso 4 queda pareado con el inciso A. Uniendo todas las respuestas nos queda:
1C, 2B, 3D, 4A
La respuesta correcta es la opción a).
Reactivo 21
Si la pendiente de una recta es igual a \frac{\sqrt{3}}{3} , calcule el ángulo que forma la recta con el eje de las ordenadas.
- 60°
- 45°
- 20°
- 30°
Solución:
De las ecuaciones fundamentales de la recta, sabemos que la pendiente m es igual a:
m=\mathrm{tan}\alpha
Donde \alpha es el ángulo entre la recta y el eje de las ordenadas.
\alpha ={\mathrm{tan}}^{-1}m
Para obtener el ángulo con las ordenadas \beta , se resta \alpha a 90°.
\beta =90-{\mathrm{tan}}^{-1}m
Sustituyendo nos queda:
\beta =90-{\mathrm{tan}}^{-1}\left(\frac{\sqrt{3}}{3}\right)=90°-30°=60°
La respuesta correcta es el inciso a).
Reactivo 22
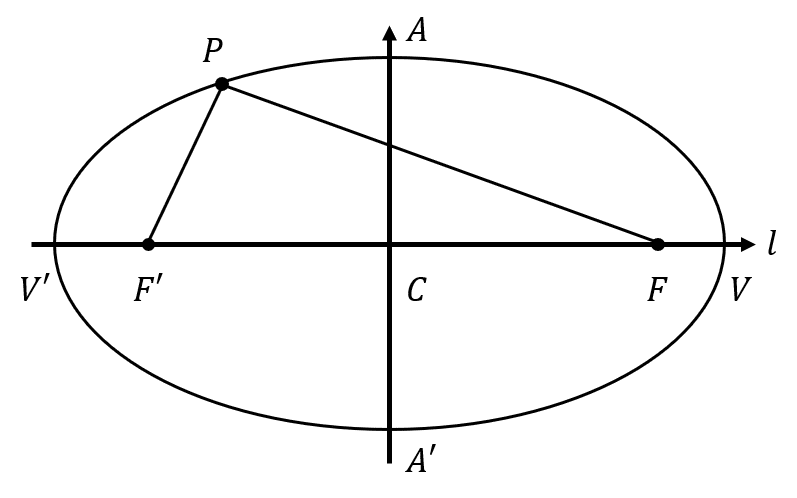
Relacionar cada parte de la elipse con el segmento de recta representado en la figura.
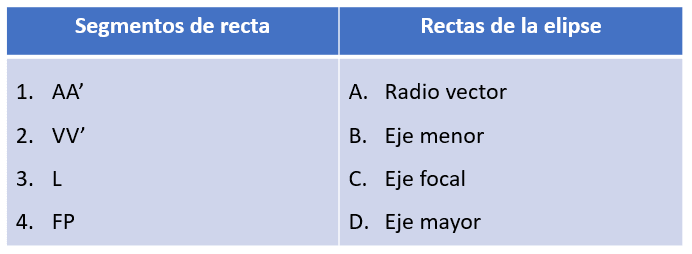
- 1B, 2D, 3A, 4C
- 1B, 2C, 3D, 4A
- 1D, 2B, 3C, 4A
- 1B, 2D, 3C, 4A
Solución:
Debemos tener presentes las partes de una elipse antes de intentar parear las dos columnas de la tabla. Iremos tomando cada una de las rectas en la columna izquierda para relacionarla con un inciso en la columna derecha.
El segmento AA’, atraviesa la elipse por su centro y es el radio de menor longitud en ella. Concluimos que AA’ es el eje menor de la elipse: 1B.
Ahora, el segmento VV’ es el más largo en la elipse correspondiente con su eje mayor, por lo tanto: 2D. La recta l contiene a los focos, a los vértices y al eje mayor, por tanto, se trata del eje focal de la elipse: 3C. Por descartes 4A.
Uniendo las soluciones:
1B, 2D, 3C, 4A.
La respuesta correcta es el inciso d).
Reactivo 23
Dada la ecuación de la recta l1:2x-y=2 , determine la ecuación de la recta que es perpendicular a l1 y pasa por el origen.
- l2: y=-2x
- l2: y=-0.5x
- l2: y=2x
- l2: y=-2x+1
Solución:
Comencemos por calcular la pendiente que debería tener la recta l2 para que sea perpendicular a l1 . La condición de perpendicularidad entre rectas es:
{m}_{1}{m}_{2}=-1
Si {m}_{1} es la pendiente de l1 , obtenemos a {m}_{2} como:
{m}_{2}=-\frac{1}{{m}_{1}}
A {m}_{1} la extraemos de la ecuación l1 .
y=2x-2
{m}_{1}=2
{m}_{2}=-\frac{1}{2}=-0.5
Sustituimos esto en la ecuación punto pendiente de la recta, donde \left({x}_{o}, {y}_{o}\right)=\left(0, 0\right) .
y-{y}_{o}={m}_{2}\left(x-{x}_{o}\right)\to y=-0.5x
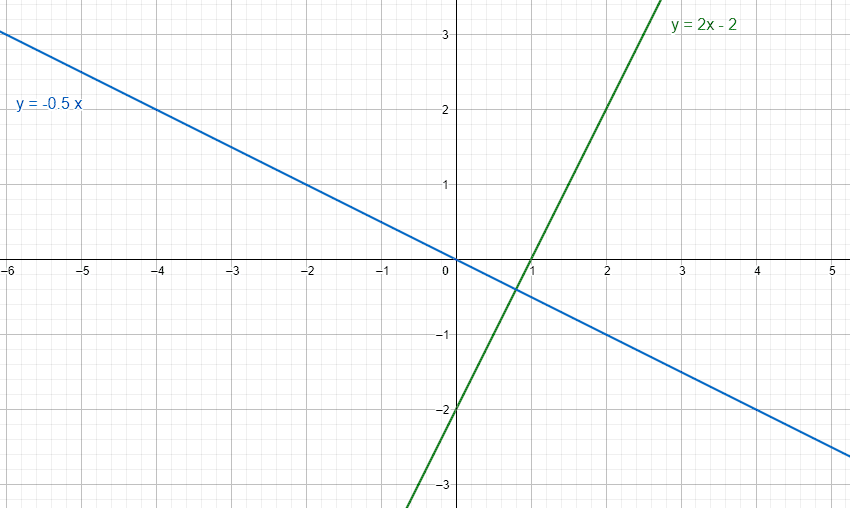
La respuesta correcta es el inciso b).
Reactivo 24
Determine el lado recto de la parábola y={x}^{2}-x-6 .
- 1
- 4
- 1/4
- 1/2
Solución:
En la ecuación de la parábola, el lado recto viene representado por la letra p y, para una parábola con eje focal paralelo a las ordenadas como en este caso, la ecuación ordinaria es:
4p\left(y-k\right)={\left(x-h\right)}^{2}
Si desarrollamos la expresión anterior nos queda:
4p\left(y-k\right)={x}^{2}-2hx+{h}^{2}\to y=\frac{{x}^{2}}{4p}-\frac{h}{2p}x+\frac{{h}^{2}}{4p}+k
y=\frac{{x}^{2}}{4p}-\frac{h}{2p}x+\frac{{h}^{2}}{4p}+k
Si aplicamos igualación de términos con la ecuación del enunciado nos queda:
\left\{\begin{array}{c}\frac{1}{4p}=1\\ -\frac{h}{2p}=-1\\ \frac{{h}^{2}}{4p}+k=-6\end{array}\right.
Podemos despejar al lado recto 4p directamente de la primera igualdad:
4p=1
El lado recto de la parábola y={x}^{2}-x-6 es 1.
Comparando con los incisos, la respuesta correcta es el a).
Reactivo 25
¿Cuál es la pendiente de la recta 4x+2y-4=0 ?
- 1/2
- -2
- 2
- -1/2
Solución:
Para obtener la pendiente de la recta, comencemos por despejar a y .
2y=-4x+4\to y=-2x+2
La pendiente es el coeficiente que multiplica a la x , por tanto:
m=-2
La respuesta correcta es el inciso b).
Reactivo 26
En base a las conclusiones que ofrece el cálculo diferencial, ¿cómo debe ser el cambio de signo de la derivada de una función f en el punto x para que el mismo sea un máximo?
- Positiva – positiva
- Negativa – positiva
- Positiva – negativa
- Negativa – negativa
Solución:
A partir del cálculo diferencial, podemos extraer información del comportamiento de la gráfica de una función estudiando el signo de la pendiente de la recta tangente antes y después de cierto número crítico.
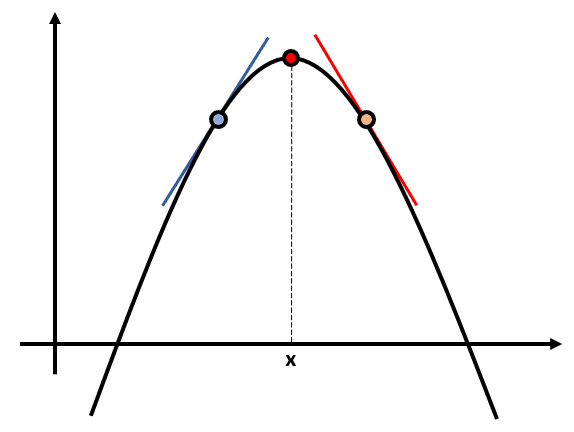
A partir de la figura vemos que, en el caso de un máximo, la pendiente de la recta tangente antes del punto es positiva y luego pasa a ser negativa. Por lo tanto, el cambio de signo que esperaríamos es: positivo – negativo. Comparando con los incisos, la respuesta correcta es el c).
Reactivo 27
Calcule el conjunto solución de la siguiente inecuación.
\frac{2x+1}{4}>x-\frac{1}{2}
- x\in \left(-\infty ,\frac{3}{2}\right]
- x\in \left(-\infty ,-\frac{3}{2}\right)
- x\in \left(-\infty ,-\frac{3}{2}\right]
- x\in \left(-\infty ,\frac{3}{2}\right)
Solución:
Aplicamos las reglas de las desigualdades para agrupar los términos con x en un mismo miembro. Multiplicamos toda la expresión por 4.
2x+1>4x-2
Pasamos a restar 4x al miembro izquierdo y a restar al 1 para el miembro derecho.
2x-4x>-2-1\to -2x>-3
Dividimos la inecuación por -2 y cambiamos el sentido de la desigualdad.
x<\frac{3}{2}
Expresando el resultado con notación de conjunto nos queda:
x\in \left(-\infty ,\frac{3}{2}\right)
La respuesta correcta es el inciso d).
Reactivo 28
Si el \underset{x\to c}{\mathrm{lim}}f\left(x\right)=2 y \underset{x\to c}{\mathrm{lim}}g\left(x\right)=-4 entonces, ¿cuánto vale el \underset{x\to c}{\mathrm{lim}}\frac{f\left(x\right)}{2g\left(x\right)} ?
- -\frac{1}{4}
- \frac{1}{4}
- \frac{1}{2}
- -4
Solución:
Debido a que tenemos los límites de las funciones, podemos aplicar la propiedad del límite del cociente de dos funciones:
\underset{x\to c}{\mathrm{lim}}\frac{f\left(x\right)}{2g\left(x\right)}=\frac{\underset{x\to c}{\mathrm{lim}}f\left(x\right)}{2\mathrm{ }\underset{x\to c}{\mathrm{lim}}g\left(x\right)}
Sustituimos los límites de las funciones:
\frac{\underset{x\to c}{\mathrm{lim}}f\left(x\right)}{2\mathrm{ }\underset{x\to c}{\mathrm{lim}}g\left(x\right)}=\frac{2}{2\left(-4\right)}=-\frac{1}{4}
Finalmente:
\underset{x\to c}{\mathrm{lim}}\frac{f\left(x\right)}{2g\left(x\right)}=-\frac{1}{4}
La respuesta correcta es el inciso a).
Reactivo 29
Calcula el valor del siguiente límite \underset{x\to 2}{\mathrm{lim}}{x}^{2}-2x+1 .
- 2
- -1
- 1
- No existe
Solución:
Comenzamos evaluando el límite que, como anticipo, no presentará indeterminación alguna por tratarse de una función polinomial.
Evaluando:
\underset{x\to 2}{\mathrm{lim}}{x}^{2}-2x+1={\left(2\right)}^{2}-2\left(2\right)+1=4-4+1=1
El límite de {x}^{2}-2x+1 cuando x tiende a 2 es 1.
La respuesta correcta es el inciso c).
Reactivo 30
Calcular los números críticos de la siguiente función.
f\left(x\right)={x}^{3}-2{x}^{2}+x+1
- x=3, x=-1
- x=\frac{1}{3}, x=1
- x=-\frac{1}{3}, x=1
- x=-3, x=1
Solución:
Los números críticos de una función, son aquellos en los que la pendiente de la recta tangente a la curva se anula. Dicho de otra forma, los puntos en los que la derivada de f se hace cero.
\frac{df}{dx}=0
Comencemos por derivar a la función.
\frac{df}{dx}=3{x}^{2}-4x+1
Ahora, igualamos a cero la expresión resultante.
3{x}^{2}-4x+1=0
Para encontrar las raíces, empleamos la fórmula de segundo grado.
x=\frac{4\pm \sqrt{{4}^{2}-4\left(3\right)\left(1\right)}}{2\left(3\right)}=\frac{4\pm \sqrt{16-12}}{6}=\frac{4\pm \sqrt{4}}{6}=\frac{4\pm 2}{6}
{x}_{1}=\frac{4+2}{6}=1, {x}_{2}=\frac{4-2}{6}=\frac{1}{3}
Los números críticos de la función son: x=\frac{1}{3}, x=1 .
La respuesta correcta es el inciso b).