Resuelve la tercera parte de los reactivos de geometría y trigonometría del examen simulacro del IPN correspondiente al apartado de matemáticas. Vamos con los ejercicios del 21 al 30.

Reactivo 21
Para localizar el _________ de un triángulo, trazamos las __________ y el punto notable resultante es la intersección de las tres rectas.
- Incentro-alturas
- Ortocentro-medianas
- Baricentro-bisectrices
- Circuncentro-mediatrices
Solución:
El problema nos pide completar la frase con el par de términos correctos faltante. Recordemos, que los puntos notables son aquellos que se forman al intersectar las rectas notables en un triángulo.
En este sentido, podemos analizar cada una de las opciones para verificar si es o no verdadera.
El incentro de un triángulo, se forma por la intersección de sus bisectrices. En la opción a) se relaciona el incentro con las alturas, aseveración que es incorrecta.
El ortocentro se forma al intersectar las alturas de un triángulo. En la opción b) se le relaciona con las medianas, motivo por el que es incorrecta.
El baricentro es el punto notable generado por la intersección de las medianas en un triángulo. La opción c) relaciona al baricentro con las bisectrices, relación que es incorrecta.
El circuncentro de un triángulo es la intersección de sus mediatrices. En la opción d) la relación es correcta, entonces: circuncentro-mediatrices. Concluimos que la respuesta correcta es la d).
Para localizar el circuncentro de un triángulo, trazamos las mediatrices y el punto notable resultante es la intersección de las tres rectas.
Reactivo 22
Calcular el valor de x de acuerdo con la figura
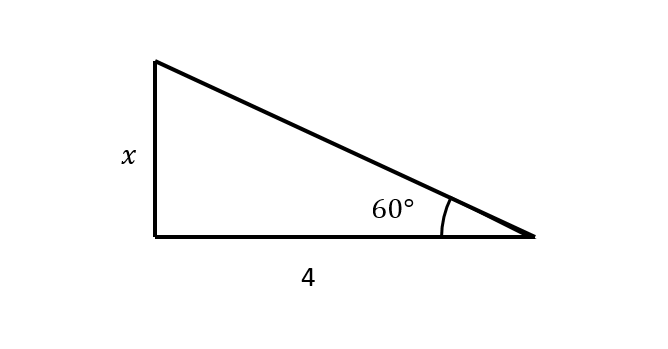
- 3 \sqrt{4}
- 4 \sqrt{3}
- \frac{4}{3} \sqrt{3}
- \frac{1}{4} \sqrt{3}
Solución:
Para resolver el problema, es necesario aplicar una identidad trigonométrica que relacione los catetos de un triángulo respecto a un ángulo. La tangente relaciona el cateto opuesto y al cateto adyacente a un ángulo determinado.
\tan \alpha=\frac{C O}{C A}
En este caso, nuestro ángulo es 60°. Opuesto a él se encuentra el lado x desconocida y en du adyacencia el lado que mide 4. Sustituyendo queda entonces:
\tan 60^{\circ}=\frac{x}{4}
La tangente de 60° vale \sqrt{3} . Procedemos a despejar para calcular finalmente a x .
x=4 \tan 60^{\circ}=4 \sqrt{3}
x=4 \sqrt{3}
Concluimos con que la respuesta correcta es la b).
Reactivo 23
Identificar la relación para encontrar el número de diagonales de un polígono de n lados.
- \frac{(n-1)(n-2)}{2}
- \frac{n(n-3)}{2}
- \frac{(n+1)}{2}
- \frac{(2 n+1)}{2}
Solución:
Para resolver este problema, podemos utilizar una de las relaciones notables de los polígonos o analizar un caso general para encontrar así la respuesta. Ya que nuestra intención se centra en el análisis y la comprensión de los problemas, vamos a deducir la respuesta paso a paso.
Primero, sabemos que un polígono tiene la misma cantidad de vértices que de lados, por tanto:
n=v
Donde n son los lados y v los vértices del polígono.
Por otro lado, las diagonales se trazan entre vértices que no son adyacentes, es decir, se trazan entre vértices que no están unidos por uno de los lados del polígono. Evidentemente, un vértice tampoco puede trazar una diagonal consigo mismo.
Lo anterior puede expresarse como que desde un vértice se trazan n - 3 diagonales. Si generalizamos esto para todos los n vértices queda la cuenta n(n-3) .
Por último, es igual la diagonal trazada de A hasta B que de B hacía A . Para eliminar esa duplicidad, dividimos por dos el resultado anterior, quedando la cantidad de diagonales totales en un polígono:
D=\frac{n(n-3)}{2}
Al comparar con las opciones que ofrece el problema, la respuesta correcta es la opción b).
Reactivo 24
Identificar el polígono en el que se puede trazar 27 diagonales en total.
- Octágono
- Hexágono
- Nonágono
- Decágono
Solución:
Para resolver este problema, basta con sustituir en la ecuación para calcular las diagonales de un polígono, el número de diagonales solicitadas y despejar de allí el número de lados que debería tener el polígono.
D=\frac{n(n-3)}{2}
Si el número de diagonales es D=27 , sustituyendo y despejando la ecuación queda como:
27=\frac{n(n-3)}{2}
54=n(n-3)
54=n^{2}-3 n
n^{2}-3 n-54=0
Se aplica la fórmula de segundo grado para encontrar las soluciones de este polinomio cuadrático:
n_{1,2}=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}=\frac{3 \pm \sqrt{9+216}}{2}=\frac{3 \pm 15}{2}
n_{1}=\frac{3+15}{2}=9
n_{2}=\frac{3-15}{2}=-6
Es claro que la respuesta correcta no puede ser -6, porque el número de lados y de vértices en un polígono son siempre positivos. Concluimos entonces que: para que un polígono tenga 27 diagonales, debe tener un total de 9 lados, es decir, debe ser un Nonágono.
La respuesta correcta es la opción c).
Reactivo 25
Calcular el área sombreada.
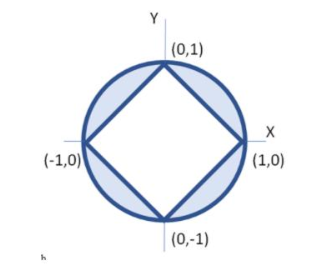
- \pi-2 \sqrt{2}
- 2 \pi-\sqrt{2}
- 2 \pi-2
- \pi-2
Solución:
Para calcular el área sombreada y cualquier área consecuencia de una disposición similar de figuras (unas dentro de otras), se toma el área de la figura externa y se le resta el área de las figuras internas.

En este caso, la figura externa es el círculo que tiene dentro a un cuadrado. Por ende, el área sombreada será igual al área del círculo menos el área del cuadrado.
Expresando esto en ecuación quedaría:
A_{s}=A_{c i r}-A_{c u a}
El área del círculo sería:
A_{c i r}=\pi r^{2}
A partir de la imagen suministrada por el problema, se aprecia que el círculo es de radio 1u. Sustituimos el valor en la ecuación:
A_{\text {cir }}=\pi(1 u)^{2}=\pi u^{2}
Nota: la “u” es abreviatura de unidad o unidades. Es una forma de denotar que la cantidad expresa una longitud, un área o un volumen.
El área del cuadrado sería:
A_{c u a}=l^{2}
Para calcular la magnitud de los lados del cuadrado, emplearemos el Teorema de Pitágoras en cualquiera de las líneas del cuadrado.
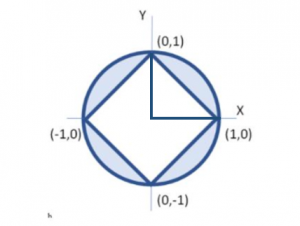
Por conveniencia, hemos escogido el lado que está en el primer cuadrante. Se forma un triángulo rectángulo cuyos catetos miden 1u y la hipotenusa desconocida es uno de los lados del cuadrado.
l=\sqrt{1^{2}+1^{2}}=\sqrt{2}
Sustituimos en la ecuación para el área del cuadrado:
A_{c u a}=(\sqrt{2})^{2}=2 u^{2}
Ahora, calculamos finalmente el área sombreada:
A_{s}=\pi-2
Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).
Reactivo 26
Identificar qué polígono tiene 20 diagonales.
Solución:
Tenemos dos opciones para resolver el problema. La primera, sería comprobar cada una de las opciones con la ecuación para calcular las diagonales de un polígono.
La segunda y más práctica, es introducir el número de diagonales en la ecuación de las diagonales de un polígono y determinar los lados que debería tener la figura. Por supuesto que aplicaremos esta segunda vía como solución al problema.
20=\frac{n(n-3)}{2}
40=n(n-3) \rightarrow n^{2}-3 n=40
n^{2}-3 n-40=0
Aplicamos la fórmula de segundo grado:
n_{1,2}=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}=\frac{3 \pm \sqrt{9+160}}{2}=\frac{3 \pm 13}{2}
n_{1}=\frac{3+13}{2}=8
n_{2}=\frac{3-13}{2}=-5
Queda claro que la respuesta correcta es n=8 , lo que corresponde a un Octágono. De las opciones que da el problema, la figura c) es un Octágono. Concluimos que la respuesta correcta es la c).
Reactivo 27
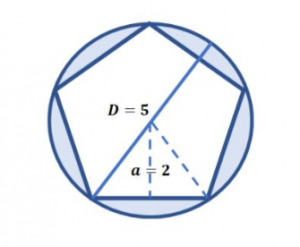
Identificar el área del pentágono inscrito en la siguiente circunferencia:
- 15
- 10
- 12
- 30
Solución:
En este caso, se solicita explícitamente el área del pentágono inscrito. Para calcularla tenemos diferentes vías con base en los datos que suministra el problema.
- Utilizando la ecuación general para el área de un pentágono
A_{p}=\frac{5 \cdot l \cdot a p}{2}
Donde l es la longitud de uno de los lados y ap es la apotema del pentágono (distancia perpendicular medida desde la mitad de uno de los lados hasta el centro del pentágono)
- Calculando el área de uno de los triángulos isósceles que se forman dentro del pentágono y luego multiplicando el resultado por 5 para obtener el área total del pentágono
A_{p}=5 A_{t r i}
Una variación de esta posible solución, sería hacerlo con los triángulos rectángulos dentro del pentágono.
En este caso, optaremos por calcular el área de los triángulos rectángulos. El motivo de esto, es que es la vía que implica menos cálculos intermedios haciendo uso de los datos suministrados por el problema.
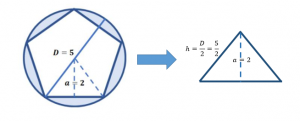
El área del triángulo rectángulo es:
A_{t r}=\frac{b a}{2}
La altura la conocemos, el problema suministra la apotema del pentágono que es igual a la altura del triángulo. La base es necesario calcularla aplicando el teorema de Pitágoras.
h^{2}=a^{2}+b^{2} \rightarrow b=\sqrt{h^{2}-a^{2}}
b=\sqrt{\left(\frac{5}{2}\right)^{2}-2^{2}}=\frac{3}{2}
A_{t r}=\frac{\left(\frac{3}{2}\right)(2)}{2}=\frac{3}{2}
Ahora, ya que el pentágono se divide en un total de 10 triángulos rectángulos, determinamos entonces el área solicitada por el problema multiplicando el área de uno por 10:
A_{p}=10 A_{t r}=10 \frac{3}{2}=15 u^{2}
Comparando con las opciones ofrecidas por el problema, la respuesta correcta es la a).
Reactivo 28
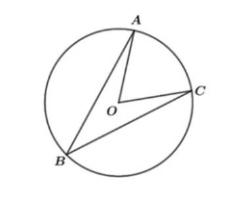
Calcular la amplitud del ángulo \lfloor A B C si se sabe que el ángulo central \left\lfloor A O C=50^{\circ}\right. .
- 50°
- 25°
- 20°
- 15°
Solución:
Similar al problema anterior, solo debemos aplicar la relación entre los ángulos central e inscrito:
\beta_{i}=\frac{\beta_{c}}{2}=\frac{\lfloor A O C}{2}
Sustituimos y calculamos el valor:
\left\lfloor A B C=\frac{\lfloor A O C}{2}=\frac{50^{\circ}}{2}=25^{\circ}\right.
La respuesta correcta al problema es la b).
Reactivo 29
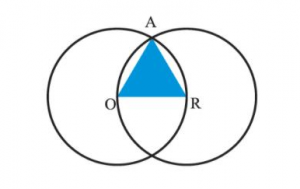
Determinar el área del triángulo OAR si O y R son los centros de circunferencias de radio 2.
- \frac{\sqrt{3}}{2} u^{2}
- \frac{\sqrt{2}}{3} u^{2}
- \sqrt{3} u^{2}
- \sqrt{2} u^{2}
Solución:
Los lados del triángulo, formado por la intersección de ambas circunferencias, tienen la misma magnitud que sus radios. Es decir, el triángulo es equilátero. Sus 3 lados son iguales y tienen como valor 2.
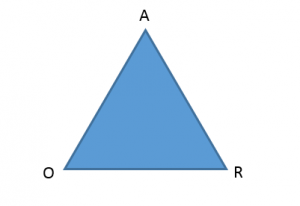
\overline{O A}=\overline{A R}=\overline{R O}=2 u
La ecuación para calcular el área de cualquier triángulo es:
A=\frac{b h}{2}
La base de este triángulo es el lado \overline{R O} que vale 2 u y la altura se puede determinar mediante el teorema de Pitágoras.
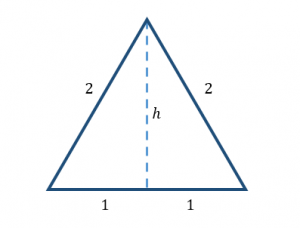
h=\sqrt{2^{2}-1^{2}}=\sqrt{3}
Sustituimos en la ecuación del área:
A=\frac{2 \sqrt{3}}{2}=\sqrt{3} u^{2}
Concluimos entonces que la respuesta correcta es la c).
Reactivo 30
En la figura, los M, N, P, Q y R dividen a la circunferencia en cinco arcos iguales. Encontrar el ángulo x .
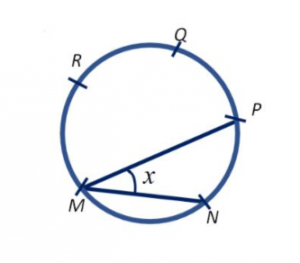
- 30°
- 36°
- 45°
- 60°
Solución:
Para dar solución al problema, debemos relacionar los arcos que se forman entre los puntos con el ángulo solicitado. Para ello, analizaremos los triángulos internos a la circunferencia.
Ya que los arcos que se forman entre cualesquiera dos puntos adyacentes son iguales, también lo serán las cuerdas que se tracen entre ellos. Si se unen los puntos N y P con una recta, se forma el triángulo MNP , cuyos lados MN y NP son de igual longitud.
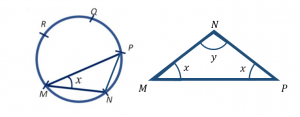
Como sabes, si dos lados en un triángulo son iguales, lo serán también los ángulos que forman dichos lados con el restante. En nuestro caso, ese ángulo es x .
Por propiedad de los triángulos, la suma de ángulos internos es siempre 180°, relación que puede expresarse:
2 x+y=180^{\circ}
Ha surgido una nueva incógnita: y . Debemos encontrar una forma de calcularla o relacionarla con x . Si analizamos un poco más a la figura, nos daremos cuenta de que si trazamos dos radios desde el centro hasta un par de puntos adyacentes, se forma otro triángulo isósceles.
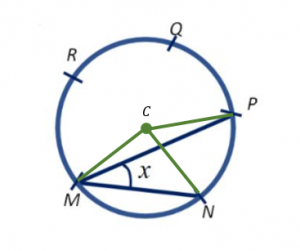
Ya que los arcos están divididos en porciones iguales, los triángulos MNC y NPC son iguales. Además, dividen al ángulo y en dos partes iguales.
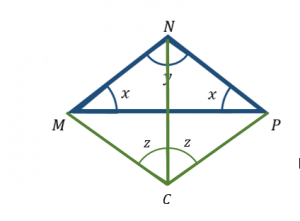
Aparece un nuevo ángulo z que tiene la particularidad de ser igual al arco MN , que es también igual al arco NP . Ya que los 5 puntos parten a la circunferencia en 5 arcos iguales, es posible calcular a z como:
z=\frac{360^{\circ}}{5}=72^{\circ}
Se aplica la misma relación de ángulos para uno de los triángulos con aristas en verde:
2 \frac{y}{2}+z=180^{\circ} \rightarrow y+z=180^{\circ}
Como z es un valor conocido, lo sustituimos para calcular a y :
y+z=180^{\circ} \rightarrow y=180^{\circ}-z
y=180^{\circ}-72^{\circ}=108^{\circ}
Con ayuda de la primera ecuación, procedemos a determinar x :
2 x+y=180^{\circ} \rightarrow x=\frac{180^{\circ}-y}{2}
x=\frac{180^{\circ}-108^{\circ}}{2}=36^{\circ}
Concluimos entonces que la respuesta correcta es la opción b).