Examen Simulador IPN Geometría y trigonometría 50 Reactivos

La parte de matemáticas representa más del 20% de tu calificación en el examen de admisión al IPN. En este examen simulacro vamos a resolver 50 reactivos de la materia de Geometría y trigonometría.

Hemos dividido este examen dividido en cinco partes para que puedas medir tu progreso de forma más organizada, toma nota de los ejercicios que se te hagan más complicados.

¿Cómo es el examen IPN?

La prueba de conocimientos del IPN es una de las más complejas del país, con tan solo una tasa de aceptación del 20% y una demanda creciente, las posibilidades de ingreso son complicadas, pero no imposibles.

El examen del IPN tiene 140 reactivos, y se divide en dos bloques, el primero de conocimientos generales:

• Matemáticas
• Competencia escrita
• Competencia lectora
• Reading comprehension (nuevo tema)
• Historia

Y, el segundo bloque es el de ciencias experimentales, donde se evalúa química, biología y física.

• IyCFM: Ingeniería y ciencias físico matemáticas
• CMD: Ciencias médico biológicas
• CSyA: Ciencias sociales y administrativas

Cada área de conocimiento tiene su propia estructura y distribución de reactivos.

Materia	IyCFM	CMB	CSyA
Matemáticas	37	33	35
Competencia escrita	20	20	25
Competencia lectora	20	20	20
Reading comprehension	10	10	10
Historia	10	10	20
Biología	9	17	10
Química	17	17	10
Física	17	13	10

Si quieres conocer todos los temas del examen de admisión al IPN visita el artículo en donde te explico todo sobre la guía y las materias que tienes que estudiar.

Temario de geometría y trigonometría

En el IPN la geometría y trigonometría se incluye dentro del temario de matemáticas, este es el temario completo del área de matemáticas:

• Funciones exponenciales y logarítmicas
  • Concepto
  • Propiedades
• Geometría euclidiana
  • Elementos básicos
  • Triángulos
  • Polígonos
  • Circunferencia
• Funciones trigonométricas
  • Representación gráfica
  • Identidades trigonométricas
  • Razones trigonométricas

Reactivo 1

Completar los logaritmos siguientes: \log 1= \_\_\_\_ \text{ y } \log 10=\_\_\_\_

1. 1, 0
2. 0, 0
3. 1, 1
4. 0, 1

Solución:

En este primer problema, solo tendremos que aplicar un par de propiedades de los logaritmos, específicamente las dos primeras señaladas en el desarrollo teórico. Antes de seguir, es necesario recordar que un logaritmo escrito sin una base señalada es de base 10.

El \log 1 es igual a cero para cualquier base, recordemos que: cualquier número elevado a cero es uno, por tanto:

\log 1=0

El \log 10 es igual a uno. En este segundo caso, tenemos al logaritmo base 10 de 10 y como lo indica la propiedad logaritmo de la base, el resultado será siempre uno por lo tanto:

\log 10=\log _{10} 10=1

Concluimos entonces que la respuesta correcta es la d).

[wpipa id=»6649″]

Reactivo 2

Resolver la ecuación logarítmica: \log _{3} 81^{x}-\log _{3} 3^{2 x}=3

1. 3
2. 6
3. 2/3
4. 3/2

Solución:

Para resolver la ecuación, debemos aplicar con astucia las propiedades de los logaritmos y los exponentes. El 81 lo podemos expresar como 3^{4} , quedando la ecuación como:

\log _{3} 81^{x}-\log _{3} 3^{2 x}=3 \rightarrow \log _{3} 3^{4 x}-\log _{3} 3^{2 x}=3

Ahora, se aplica la propiedad logaritmo de una potencia:

\log _{3} 3^{4 x}-\log _{3} 3^{2 x}=3 \rightarrow 4 x \log _{3} 3-2 x \log _{3} 3=3

El logaritmo de un número que es igual a la base del logaritmo tiene como resultado uno:

4 x \log _{3} 3-2 x \log _{3} 3=3 \rightarrow 4 x(1)-2 x(1)=3

4 x-2 x=3

Hemos transformado a la ecuación logarítmica en una ecuación lineal fácil de resolver. Procedemos a encontrar el valor de x .

4 x-2 x=3 \rightarrow x= 3/2

Ya que la x se encuentra en los exponentes de los argumentos, nunca dará como resultado un valor negativo dentro de ellos. Concluimos entonces que: la respuesta correcta es la d).

Reactivo 3

¿Cuál es el valor de e^{\frac{1}{2} \ln 9} ?

1. 12
2. 9
3. 3
4. 2

Solución:

Para encontrar el valor solicitado, nos valdremos de la siguiente deducción:

Se sabe que:

\log _{b} x=n \rightarrow b^{n}=x

Si sustituimos n=\log _{b} x \text { en } b^{n}=x obtenemos que:

b^{\log _{b} x}=x

Es decir: cualquier número b elevado al logaritmo base b de una cantidad x tiene como resultado a x . Con esto demostrado, solo tenemos que trabajar un poco la expresión enunciada en el problema para aplicar esta deducción.

e^{\frac{1}{2} \ln 9}=e^{\frac{1}{2} \ln 3^{2}}

Propiedad del logaritmo de una potencia:

e^{\frac{1}{2} \ln 3^{2}}=e^{\frac{2}{2} \ln 3}=e^{\ln 3}

Ha quedado el número e elevado al logaritmo base e de 3, por lo tanto:

b^{\log _{b} x}=x \rightarrow e^{\ln 3}=3

Concluimos que la respuesta correcta es la c).

Reactivo 4

Relacionar cada logaritmo con su valor correspondiente:

1. 1B, 2D, 3A, 4C
2. 1B, 2C, 3D, 4A
3. 1C, 2A, 3D, 4B
4. 1C, 2A, 3B, 4D

Solución:

Iremos resolviendo cada logaritmo de la columna izquierda, para luego asociarlo con el valor correcto en la columna derecha.

1. \log _{2} 8

Se transforma al 8 como 2^{3} y se aplican propiedades:

\log _{2} 8=\log _{2}\left(2^{3}\right)=3 \log _{2}(2)=3(1)=3

Concluimos: 1B.

2. \log _{3} 9

El truco será similar, el 9 se escribe como 3^{2} :

\log _{3} 9=\log _{3}\left(3^{2}\right)=2 \log _{3}(3)=2(1)=2

Concluimos: 2C.

3. \log _{4} 2

Aquí debemos aplicar un truco con las potencias para emplear la propiedad de logaritmo de una potencia:

2=\left(2^{2}\right)^{\frac{1}{2}}=4^{\frac{1}{2}}

Sustituimos y resolvemos:

\log _{4} 2=\log _{4}\left(4^{\frac{1}{2}}\right)=\frac{1}{2} \log _{4} 4=\frac{1}{2}(1)=\frac{1}{2}

Concluimos: 3D.

4. \log _{4} 1

Este último tiene solución directa, pues responde a la propiedad logaritmo de la unidad:

\log _{4} 1=0

Concluimos: 4A.

Finalmente, la respuesta correcta es la b) 1B, 2C, 3D, 4A.

Reactivo 5

Representar \log _{\frac{1}{3}} \frac{1}{3}=1 en forma exponencial.

1. \left(\frac{1}{3}\right)^{1}=\frac{1}{3}
2. (3)^{-1}=\frac{1}{3}
3. \left(\frac{1}{3}\right)^{-1}=3
4. (3)^{1}=3

Solución:

Llevar a la forma exponencial el logaritmo indicado es sencillo, recordemos que:

\log _{b} x=n \rightarrow b^{n}=x

Donde:

• b=\frac{1}{3}
• x=\frac{1}{3}
• n=1

Por lo tanto:

b^{n}=x \rightarrow\left(\frac{1}{3}\right)^{1}=\frac{1}{3}

Se concluye que la respuesta correcta es la a). Cabe acotar que la respuesta b) también es correcta, ya que \frac{1}{3}=(3)^{-1} , tanto la respuesta a) como la b) son equivalentes.

Reactivo 6

Calcular los valores de x \text { У } y \text { si } \overline{A B}|| \overline{C D} .

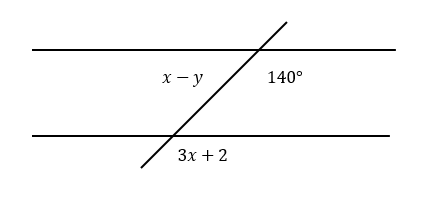
1. x=180^{\circ} \quad y=140^{\circ}
2. x=50^{\circ} \quad y=10^{\circ}
3. x=46^{\circ} \quad y=6^{\circ}
4. x=30^{\circ} \quad y=45^{\circ}

Solución:

Nuevamente, debemos hacer uso de las relaciones entre ángulos que se forman al cortar dos rectas paralelas.

Las relaciones indican que:

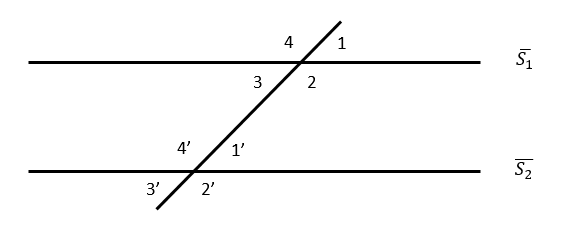
\hat{1}=\widehat{1}^{\prime}

\hat{2}=\widehat{2}^{\prime}

\hat{3}=\widehat{3}^{\prime}

\hat{4}=\widehat{4}^{\prime}

Llevadas a nuestro problema \hat{2}=140^{\circ} y \widehat{2^{\prime}}=3 x+2 . Entonces:

3 x+2=140^{\circ}(I)

Para el ángulo restante debemos ser más audaces. Aplicaremos la relación de ángulos suplementarios.

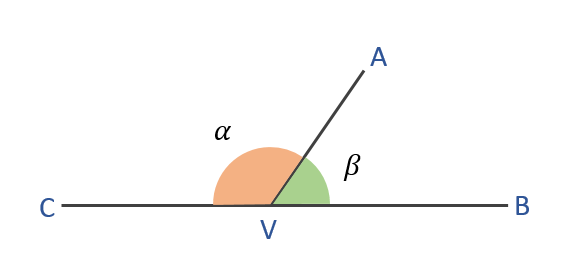
\alpha+\beta=180^{\circ}

Escogeremos a \alpha=x-y \text { у } \beta=140^{\circ} , es indistinto el orden de asignación en este caso. Recuerda que la suma es conmutativa. Sustituyendo todo quedaría:

x-y+140^{\circ}=180^{\circ}

x-y=40^{\circ}(I I)

Despejamos de (I) el valor de x :

3 x+2=140^{\circ} \rightarrow x=46^{\circ}

Sustituimos el resultado en (I I) para calcular y :

x-y=40^{\circ} \rightarrow y=6^{\circ}

Concluimos entonces que x=46^{\circ} y=6^{\circ} . La respuesta correcta es la c).

Reactivo 7

Resolver la ecuación logarítmica: \log _{\frac{1}{5}} x=\log _{\frac{1}{5}} 6+\log _{\frac{1}{5}} 5

1. 25
2. 30
3. 36
4. 40

Solución:

Este último problema es bastante sencillo de solucionar. Primero, apliquemos la propiedad del logaritmo del producto de dos números en sentido inverso al segundo miembro de la ecuación:

\log _{\frac{1}{5}} x=\log _{\frac{1}{5}} 6 * 5 \rightarrow \log _{\frac{1}{5}} x=\log _{\frac{1}{5}} 30

Ahora, ambos logaritmos poseen la misma base, lo que quiere decir que la única condición que falta para que sean iguales, es que sus argumentos sean iguales, por lo tanto:

x=30

Concluimos entonces que la respuesta correcta es la b).

Reactivo 8

Encontrar el valor de x de acuerdo con la siguiente expresión 4^{x+2}=4

1. -2
2. -1
3. 1
4. 2

Solución:

El problema puede resolverse por el primer método o por el segundo. Ya que las bases a ambos lados de la ecuación son de forma directa equivalentes, aplicaremos el primer método:

4^{x+2}=4 \rightarrow x+2=1

Despejamos a x de la ecuación y obtenemos que:

x+2=1 \rightarrow x=-1

Concluimos entonces que la respuesta correcta es la b).

Reactivo 9

Calcular la longitud del segmento \overline{D A} que se muestra en la siguiente figura y en el cual se cumple que \overline{A C}=2 \overline{D B} .

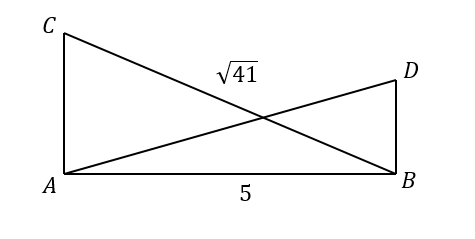
1. \sqrt{29}
2. \frac{\sqrt{41}}{2}
3. 4
4. 2

Solución:

El segmento \overline{D A} es la hipotenusa del triángulo A B D , del que solo conocemos uno de sus catetos \overline{A B}=5 . Este último es también cateto del triángulo A B C para el que también conocemos a su hipotenusa, el segmento \overline{C B}=\sqrt{41} .

Con la relación dada por el problema \overline{A C}=2 \overline{D B} , podemos primero calcular el cateto \overline{A C} del triángulo A B C , sustituirlo en la relación y con el teorema de Pitágoras aplicado en el triángulo A B D determinar al segmento \overline{D A} solicitado por el problema.

Para el triángulo A B C :

• Cateto 1: \overline{A B}=5
• Hipotenusa: \overline{C B}=\sqrt{41}
• Cateto 2: \overline{A C}=?

Según el Teorema de Pitágoras:

c_{1}=\sqrt{h^{2}-c^{2}{ }_{2}} \rightarrow \overline{A C}=\sqrt{\overline{C B}^{2}-\overline{A B}^{2}}

Sustituimos valores y calculamos:

\overline{A C}=\sqrt{(\sqrt{41})^{2}-(5)^{2}}=4

Con la relación \overline{A C}=2 \overline{D B} procedemos a determinar el otro cateto del triángulo A B D :

\overline{A C}=2 \overline{D B} \rightarrow \overline{D B}=\frac{\overline{A C}}{2}

\therefore \overline{D B}=\frac{4}{2}=2

Aplicamos finalmente el teorema de Pitágoras al triángulo A B D para calcular a \overline{D A} :

• Cateto 1: \overline{D B}=2
• Cateto 2: \overline{A B}=5
• Hipotenusa: \overline{D A}=?

\overline{D A}=\sqrt{\overline{D B}^{2}+\overline{A B}^{2}}

\overline{D A}=\sqrt{(2)^{2}+(5)^{2}}=\sqrt{29}

Concluimos entonces en que la respuesta correcta es la a).

Reactivo 10

Asociar los valores de radianes con sus respectivos equivalentes en grados.

1. 1C, 2A, 3B, 4D
2. 1C, 2A, 3D, 4B
3. 1D, 2C, 3B, 4A
4. 1D, 2B, 3C, 4A

Solución:

Para resolver este problema, haremos uso de la fórmula que transforma de radianes a grados sexagesimales.

\text { grados }=\frac{180^{\circ}}{\pi} \mathrm{rad}

Así, iremos transformando a la columna izquierda a grados para comparar el resultado con la columna derecha.

Para 1.

Transformamos \frac{\pi}{2} a grados:

\text { grados }=\frac{180^{\circ}}{\pi} \frac{\pi}{2}=90^{\circ}

Comparando con la columna derecha, la opción correcta sería 1C.

Para 2.

Transformamos \frac{\pi}{6} a grados:

\text { grados }=\frac{180^{\circ}}{\pi} \frac{\pi}{6}=30^{\circ}

Comparando con la columna derecha, la opción correcta sería 2A.

Para 3.

Transformamos \frac{3 \pi}{4} a grados:

\text { grados }=\frac{180^{\circ}}{\pi} \frac{3 \pi}{4}=135^{\circ}

Comparando con la columna derecha, la opción correcta sería 3B.

Para 4.

Transformamos \frac{4 \pi}{3} a grados:

\text { grados }=\frac{180^{\circ}}{\pi} \frac{4 \pi}{3}=240^{\circ}

Comparando con la columna derecha, la opción correcta sería 4D.

Uniendo los resultados obtenidos: 1C, 2A, 3B, 4D. La respuesta correcta es la a).