¿Vas a presentar el examen de ingreso a la UNAM? Pon a prueba tus conocimientos con este examen simulacro del área de Matemáticas de los temas de la guía de estudios de la UNAM (los reactivos abarcan las 4 áreas).

En este tutorial vamos a resolver los primeros 30 reactivos de un total de 50 del Simulador de Matemáticas con ejercicios similares al examen real, de cara a la prueba de ingreso a la Universidad Nacional Autónoma de México.
Intenta resolverlos por tu cuenta antes de consultar a la solución. Es necesario que comprendas muy bien los temas del examen, tu calificación es proporcional esfuerzo que dediques durante tu preparación.
Recuerda que tienes 3 horas para resolver los 120 reactivos del examen, practicar con este simulacro te ayudara a desarrollar agilidad al momento de responder los ejercicios.
Estructura del examen UNAM
El examen de ingreso a la UNAM tiene una extensión de 120 problemas, la cantidad de reactivos por área varía en función al área que pertenece tu carrera. La siguiente tabla resume la estructura del examen UNAM para las 4 áreas.
| Temas | Área 1 | Área 2 | Área 3 | Área 4 |
|---|---|---|---|---|
| Español | 18 | 18 | 18 | 18 |
| Matemáticas | 26 | 24 | 24 | 22 |
| Física | 16 | 12 | 10 | 10 |
| Química | 10 | 13 | 10 | 10 |
| Biología | 10 | 13 | 10 | 10 |
| Historia universal | 10 | 10 | 14 | 10 |
| Historia de México | 10 | 10 | 14 | 10 |
| Literatura | 10 | 10 | 10 | 10 |
| Geografía | 10 | 10 | 10 | 10 |
| Filosofía | NA | NA | NA | 10 |
| Total | 120 | 120 | 120 | 120 |
¿Quieres conocer todos los detalles del examen a la UNAM?
Adicional a la prueba de admisión, algunas carreras en la UNAM poseen modalidad de ingreso indirecto. Es decir, debes presentar pruebas adicionales que dependen de la facultad a la que deseas ingresar.
¿Cómo estudiar matemáticas?
Matemáticas es una asignatura en la que necesitas leer y comprender las bases para poder utilizarlas resolviendo ejercicios.
El primer error suele ser pasar directo a realizar reactivos, intentando cualquier cosa y frustrándote en el camino. Esto puede repercutir en tus aciertos del examen, disminuyendo la nota final.
Te dejo una serie de tips para que mejores tu rendimiento al momento de estudiar esta increíble asignatura.
- Revisa la bibliografía recomendada en la guía UNAM área y selecciona un par textos de tu agrado. No es necesario leerlos por completo, el motivo de esto es: algunos temas se explican mejor en unos libros que en otros.
- Lee la teoría y resuelve los ejemplos. Por más simple que parezca una propiedad o un teorema, conocer su origen y demostración te ayudará a nunca olvidarla. Hay problemas cuya solución rápida se da a través de un teorema.
- Si un tema parece difícil de comprender, busca otro libro. Los autores suelen enfocarse en determinados temas a la hora de escribir sus textos, por esta razón, suelen desbordar demasiados detalles que, al ser principiantes, pueden abrumarnos al estudiar.
- Practica con ejercicios… pero de forma inteligente. Resolver un ejercicio intentando cualquier idea no es la mejor forma de practicar lo aprendido. Analiza el problema, comprende lo que te solicita, identifica las herramientas matemáticas para resolverlo y crea un plan sistemático para resolverlo. Si no funciona pregúntate, ¿qué hice mal?, ¿hay un concepto que no apliqué correctamente?
Temario matemáticas UNAM
En la siguiente lista tienes el temario de matemáticas para todas las áreas de la UNAM.
Recuerda que Área 1 y 2, poseen una parte adicional dedicada a cálculo diferencial e integral. Puedes acceder a mayor información sobre el examen y la convocatoria UNAM en el resto de artículos que hemos preparado para ti.
- Operaciones con números reales, complejos y expresiones algebraicas
- Números reales
- Suma y resta
- Multiplicación y división
- Raíces y potencias con exponente racional
- Números complejos
- Suma y resta
- Multiplicación
- Expresiones algebraicas
- Suma y resta
- Multiplicación y división
- Raíces y potencias con exponente racional
- Operaciones con radicales
- Números reales
- Productos notables y factorización
- Binomio de Newton a+bn, n ∈N
- Teorema del residuo y del factor
- Simplificación de fracciones algebraicas
- Operaciones con fracciones algebraicas
- Ecuaciones
- Ecuación, identidad y propiedades de la igualdad
- Ecuaciones de primer grado
- Ecuaciones de segundo grado
- Desigualdades
- Desigualdad de primer grado en una variable y sus propiedades
- Sistemas de ecuaciones
- Sistemas de dos ecuaciones lineales con dos incógnitas
- Métodos de solución
- Sistemas de tres ecuaciones lineales con tres incógnitas
- Métodos de solución (Regla de Cramer)
- Sistemas de dos ecuaciones lineales con dos incógnitas
- Funciones algebraicas
- Dominio, contradominio y regla de correspondencia
- Rango o imagen
- Gráfica
- Implícitas y explícitas
- Crecientes y decrecientes
- Continuas y discontinuas
- Álgebra de funciones
- Trigonometría
- Trigonometría básica
- Medida de un ángulo (conversión de grados a radianes y de radianes a grados)
- Razones trigonométricas
- Resolución de triángulos rectángulos
- Ley de los Senos y Ley de los Cosenos
- Resolución de triángulos oblicuángulos
- Razones trigonométricas para un ángulo en cualquier cuadrante. Fórmulas de reducción
- Funciones trigonométricas
- El círculo trigonométrico
- Funciones trigonométricas directas
- Dominio y rango
- Periodo y amplitud
- Desfasamiento
- Asíntotas de la gráfica
- Trigonometría básica
- Funciones exponenciales y logarítmicas
- Dominio y rango
- Gráficas y asíntotas
- Recta
- Distancia entre dos puntos
- Coordenadas de un punto que divide a un segmento de acuerdo con una razón dada
- Pendiente de una recta
- Formas de la ecuación de la recta y su gráfica
- Condiciones de paralelismo y perpendicularidad
- Distancia de un punto a una recta
- Ecuaciones de las medianas, mediatrices y alturas de un triángulo. Puntos de intersección (ortocentro, circuncentro y baricentro)
- Circunferencia
- Circunferencia como lugar geométrico
- Formas ordinarias (canónica) y general de la ecuación de la circunferencia con centro en el origen
- Ecuación de la circunferencia con centro en (h, k) en las formas ordinaria y general
- Elementos de una circunferencia
- Parábola
- Parábola como lugar geométrico
- Formas ordinaria y general de la ecuación de la parábola cuando el vértice está en el origen y el eje focal coincide con alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la parábola cuando el vértice está en un punto cualquiera del plano y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una parábola
- Elipse
- Elipse como lugar geométrico
- Relación entre los parámetros a, b y c
- Formas ordinaria y general de la ecuación de la elipse con centro en el origen y eje focal sobre alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la elipse con centro fuera del origen y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una elipse
- Hipérbola
- Hipérbola como lugar geométrico
- Relación entre los parámetros de la hipérbola a, b y c
- Formas ordinaria y general de la ecuación de la hipérbola con centro en el origen y eje focal sobre alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la hipérbola con centro fuera del origen y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una hipérbola
- Ecuación general de segundo grado
- Las cónicas
- Ecuación general de segundo grado
- Criterios para identificar a la cónica que representa una ecuación de segundo grado
- Traslación de ejes
Simulador de Matemáticas UNAM
Vamos con el desarrollo paso a paso de los primeros 30 reactivos del simulador real de matemáticas UNAM.
Reactivo 1
Resuelva la siguiente expresión aritmética, aplicando las propiedades de la suma y la multiplicación.
1+\left(-3+4\times 5\right)+\frac{4}{2}-5
- -15
- 15
- 7
- 4
Solución:
En los ejercicios de aritmética que involucran operaciones combinadas y signos de agrupación, debemos resolver paso a paso aplicando las respectivas reglas de signos. Para el ejercicio del enunciado, debemos comenzar por resolver el interior de los paréntesis.
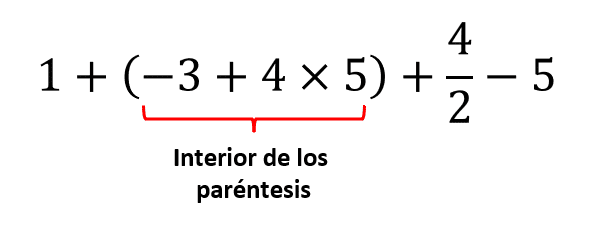
Dentro de ellos, se encuentra el menos 3 sumando al producto de 4 por 5. Recordando la jerarquía de operaciones, primero se resuelven las multiplicaciones y divisiones y luego las sumas y restas. Aplicando esto último nos queda:
1+\left(-3+4\times 5\right)+\frac{4}{2}-5=1+\left(-3+20\right)+\frac{4}{2}-5
Ahora podemos restarle 3 al 20, para deshacernos de los paréntesis.
1+\left(-3+20\right)+\frac{4}{2}-5=1+\left(17\right)+\frac{4}{2}-5=1+17+\frac{4}{2}-5
Examinando la expresión, vemos que nos queda una división indicada en forma de fracción: \frac{4}{2} , la resolvemos:
1+17+\frac{4}{2}-5=1+17+4÷2-5=1+17+2-5
Resolvemos las sumas y restas de izquierda a derecha.
1+17+2-5=18+2-5
18+2-5=20-5
20-5=15
Finalmente:
1+\left(-3+4\times 5\right)+\frac{4}{2}-5=15
Comparando con los incisos, concluimos que la respuesta correcta es el b).
Reactivo 2
Obtenga el resultado de la siguiente operación con radicales.
\sqrt{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)+2}
- 2
- \sqrt{2}
- 4
- 1
Solución:
Comencemos por identificar la operación de mayor jerarquía dentro de la raíz cuadrada. En este caso, vemos el producto de los conjugados \left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right) a los cuales se les suma el 2.
No podemos operar \sqrt{3} con el 1 dentro de los paréntesis, ya que el primero es un radical no simplificado y el segundo es un número entero. En base a las reglas de jerarquía, resolvemos primero el producto \left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right) , aplicando la propiedad distributiva.
\sqrt{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)+2}=\sqrt{\sqrt{3}\left(\sqrt{3}+1\right)-1\left(\sqrt{3}+1\right)+2}
Aplicamos nuevamente distributiva para deshacer los paréntesis.
\sqrt{\sqrt{3}\left(\sqrt{3}+1\right)-1\left(\sqrt{3}+1\right)+2}=\sqrt{3+\sqrt{3}-\sqrt{3}-1+2}
Se cancela +\sqrt{3} con el -\sqrt{3} .
\sqrt{3-1+2}
Resolvemos las sumas y restas de izquierda a derecha.
\sqrt{3-1+2}=\sqrt{2+2}=\sqrt{4}
Finalmente, resolvemos la raíz cuadrada del 4.
\sqrt{4}=2
\sqrt{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)+2}=2
En base a los incisos, la respuesta correcta es el a).
Consulta la lista completa de carreras de la UNAM
Reactivo 3
Calcule el resultado de la siguiente operación con números complejos.
\frac{1+i}{2+3i}
- 3-2i
- \frac{1}{13}-\frac{5}{13}i
- 5+13i
- \frac{5}{13}-\frac{1}{13}i
Solución:
Para resolver el cociente de dos complejos en forma cartesiana, empleamos el siguiente truco matemático:
Dados {z}_{1} y {z}_{2} números complejos, el cociente es igual al producto de {z}_{1} con el conjugado de {z}_{2} ( \stackrel{-}{{z}_{2}} ) sobre el módulo de {z}_{2} al cuadrado.
\frac{{z}_{1}}{{z}_{2}}=\frac{{z}_{1}\cdot \stackrel{-}{{z}_{2}}}{{\left|{z}_{2}\right|}^{2}}
Recordemos que el conjugado de un complejo a+bi es el mismo número, pero con la parte imaginaria cambiada de signo: a-bi . Por otro lado, el módulo de un complejo se calcula como: \left|a+bi\right|=\sqrt{{a}^{2}+{b}^{2}} .
Aplicando todo esto al ejercicio tenemos:
{z}_{1}=1+i, {z}_{2}=2+3i
\stackrel{-}{{z}_{2}}=2-3i
{\left|{z}_{2}\right|}^{2}={2}^{2}+{3}^{2}=13
Por tanto:
\frac{1+i}{2+3i}=\frac{\left(1+i\right)\left(2-3i\right)}{{\left|2+3i\right|}^{2}}=\frac{\left(1+i\right)\left(2-3i\right)}{13}
Nos queda resolver el producto del numerador. Puedes aplicar la fórmula o propiedad distributiva. La fórmula es la mejor opción durante el examen, ya que tomará menos tiempo.
Producto de dos complejos en forma cartesiana:
\left(a+bi\right)\left(c+di\right)=\left(ac-bd\right)+\left(ad+bc\right)i
Aplicando nos queda:
\frac{\left(1+i\right)\left(2-3i\right)}{13}=\frac{\left(2+3\right)+\left(-3+2\right)i}{13}=\frac{5-i}{13}
Finalmente:
\frac{1+i}{2+3i}=\frac{5}{13}-\frac{1}{13}i
La respuesta correcta es el inciso d).
Reactivo 4
Resuelva la siguiente operación de polinomios.
\left(3{x}^{2}-x+1\right)÷\left(x-1\right)
- 3x+2+\frac{3}{x-1}
- 3x+2+\frac{3}{x+1}
- 3x+2+\frac{1}{x-1}
- 3x+2-\frac{3}{x-1}
Solución:
Para calcular el cociente entre dos polinomios, primero debemos identificar que el grado del polinomio numerador sea mayor o igual al grado del polinomio numerador. En nuestro caso, el polinomio numerador es de grado 2 y el denominador grado 1.
El siguiente paso es aplicar el algoritmo de la división sintética.
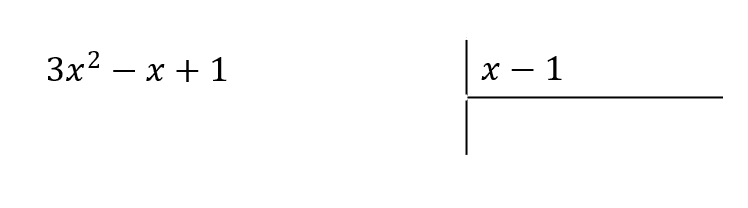
Debemos escoger un monomio que multiplicado por x-1 y cambiado de signo nos permita cancelar a 3{x}^{2} . Este monomio sería 3x .

Ahora, debemos encontrar un monomio que multiplicado por x-1 y cambiado de signo, cancele a 2x . El monomio en cuestión es 2.
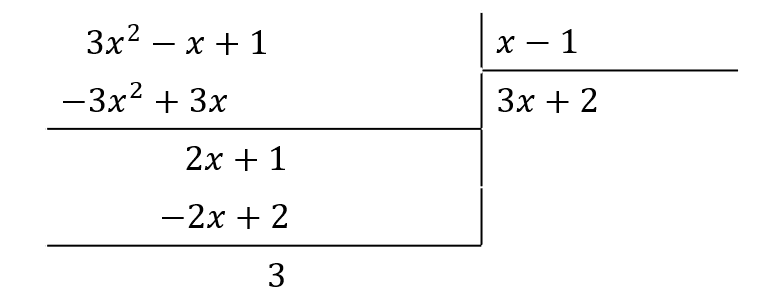
Reescribiendo el resultado nos queda:
\left(3{x}^{2}-x+1\right)÷\left(x-1\right)=3x+2+\frac{3}{x-1}
Concluimos indicando como respuesta correcta la a).
Reactivo 5
Al desarrollar la expresión {\left(2a-b\right)}^{3} se obtiene:
- {a}^{3}-12{a}^{2}b+a{b}^{2}-{b}^{3}
- 8{a}^{3}-12{a}^{2}b+a{b}^{2}-{b}^{3}
- {a}^{3}-2{a}^{2}b+a{b}^{2}-{b}^{3}
- 8{a}^{3}-12{a}^{2}b+6a{b}^{2}-{b}^{3}
Solución:
Para desarrollar esta expresión, debemos aplicar la fórmula del producto notable de un binomio con signo negativo elevado al cubo.
Producto notable del binomio al cubo.
(x-y{)}^{3}={x}^{3}-3{x}^{2}y+3x{y}^{2}-{y}^{3}
Sustituyendo los valores nos queda:
{\left(2a-b\right)}^{3}={\left(2a\right)}^{3}-3{\left(2a\right)}^{2}\left(b\right)+3\left(2a\right){\left(b\right)}^{2}-{\left(b\right)}^{3}
Simplificando:
{\left(2a\right)}^{3}-3{\left(2a\right)}^{2}\left(b\right)+3\left(2a\right){\left(b\right)}^{2}-{\left(b\right)}^{3}=8a-12{a}^{2}b+6a{b}^{2}-{b}^{3}
El resultado de desarrollar {\left(2a-b\right)}^{3} es:
8a-12{a}^{2}b+6a{b}^{2}-{b}^{3}
La respuesta correcta es la opción d).
Reactivo 6
Encuentre la factorización del trinomio 2{x}^{2}-3x-2 .
- \left(x-2\right)\left(2x+1\right)
- \left(x+2\right)\left(2x+1\right)
- \left(x-2\right)\left(2x-1\right)
- \left(x+2\right)\left(2x-1\right)
Solución:
Para factorizar trinomios cuadrados de la forma a{x}^{2}+bx+c , tenemos varios métodos, pero el más rápido en este caso será la fórmula de segundo grado:
{x}_{\mathrm{1,2}}=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}
Según el trinomio del enunciado, los coeficientes a, b y c tienen como valores 2, -3 y -2 respectivamente. Sustituyendo en la fórmula nos queda:
{x}_{\mathrm{1,2}}=\frac{-\left(-3\right)\pm \sqrt{{\left(-3\right)}^{2}-4\left(2\right)\left(-2\right)}}{2\left(2\right)}
Simplificamos las operaciones.
{x}_{\mathrm{1,2}}=\frac{3\pm \sqrt{9+16}}{4}
{x}_{\mathrm{1,2}}=\frac{3\pm \sqrt{25}}{4}=\frac{3\pm 5}{4}
{x}_{1}=\frac{3+5}{4}=\frac{8}{4}=2
{x}_{2}=\frac{3-5}{4}=-\frac{1}{2}
Escribimos la expresión factorizada como:
2{x}^{2}-3x-2=\left(x-2\right)\left(x+\frac{1}{2}\right)=\frac{\left(x-2\right)\left(2x+1\right)}{2}
Cuando factorizamos un polinomio, estamos encontrando los valores en los que se hace cero.
\frac{\left(x-2\right)\left(2x+1\right)}{2}=0
Por esta razón, podemos despejar el 2 del denominador para simplificar el resultado.
\left(x-2\right)\left(2x+1\right)=0
Concluimos entonces que la forma factorizada es:
2{x}^{2}-3x-2=\left(x-2\right)\left(2x+1\right)
Comparando con los incisos, la respuesta correcta es la a).
Reactivo 7
Determine la forma simplificada de la siguiente fracción algebraica.
\frac{2xy-2x+3-3y}{18{x}^{3}+15{x}^{2}-63x}
- \frac{y}{3x\left(3x+7\right)}
- \frac{y-1}{x\left(3x+7\right)}
- \frac{y-1}{3x\left(3x-7\right)}
- \frac{y-1}{3x\left(3x+7\right)}
Solución:
A simple vista, identificamos la extracción de factor común 3x en el denominador y que es necesario agrupar términos en el numerador. Aplicando esto a la fracción nos queda:
\frac{2xy-2x+3-3y}{18{x}^{3}+15{x}^{2}-63x}=\frac{2xy-2x+3-3y}{3x\left(6{x}^{2}+5x-21\right)}
Agrupamos términos en el numerador.
\frac{2xy-2x+3-3y}{3x\left(6{x}^{2}+5x-21\right)}=\frac{2x\left(y-1\right)-3\left(y-1\right)}{3x\left(6{x}^{2}+5x-21\right)}
\frac{2x\left(y-1\right)-3\left(y-1\right)}{3x\left(6{x}^{2}+5x-21\right)}=\frac{\left(2x-3\right)\left(y-1\right)}{3x\left(6{x}^{2}+5x-21\right)}
El siguiente paso en nuestra simplificación, consistirá en factorizar el trinomio del denominador. Para ello, aplicaremos la fórmula de segundo grado.
{x}_{\mathrm{1,2}}=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}
Sustituimos los valores y resolvemos.
{x}_{\mathrm{1,2}}=\frac{-5\pm \sqrt{{5}^{2}-4\left(6\right)\left(-21\right)}}{2\left(6\right)}=\frac{-5\pm 23}{12}
{x}_{1}=\frac{-5+23}{12}=\frac{18}{12}=\frac{3}{2}
{x}_{2}=\frac{-5-23}{12}=-\frac{7}{3}
Expresamos al trinomio en la forma factorizada.
6{x}^{2}+5x-21=\left(x-\frac{3}{2}\right)\left(x+\frac{7}{3}\right)=\left(2x-3\right)\left(3x+7\right)
Sustituimos en la fracción y simplificamos.
\frac{\left(2x-3\right)\left(y-1\right)}{3x\left(6{x}^{2}+5x-21\right)}=\frac{\left(2x-3\right)\left(y-1\right)}{3x\left(2x-3\right)\left(3x+7\right)}=\frac{y-1}{3x\left(3x+7\right)}
Llegados a este punto, no es posible continuar simplificando la fracción. Concluimos que:
\frac{2xy-2x+3-3y}{18{x}^{3}+15{x}^{2}-63x}=\frac{y-1}{3x\left(3x+7\right)}
La respuesta correcta es el inciso d).
Reactivo 8
Obtenga el resultado de la siguiente operación entre fracciones algebraicas.
\frac{1}{x-4}-\frac{1}{x-3}
- \frac{x}{{x}^{2}-7x+12}
- \frac{1}{{x}^{2}-7x+12}
- \frac{1}{{x}^{2}-7x-12}
- \frac{1}{{x}^{2}-7x}
Solución:
Las operaciones entre fracciones algebraicas, se resuelven de la misma forma que las fracciones con números enteros. La clara diferencia, es que las operaciones indicadas luego de sumar o restar las fracciones, serán productos entre binomios.
Aplicamos la regla para la resta de fracciones.
\frac{1}{x-4}-\frac{1}{x-3}=\frac{x-3-\left(x-4\right)}{\left(x-4\right)\left(x-3\right)}
Simplificamos la expresión.
\frac{x-3-\left(x-4\right)}{\left(x-4\right)\left(x-3\right)}=\frac{x-3-x+4}{{x}^{2}-3x-4x+12}=\frac{1}{{x}^{2}-7x+12}
Finalmente:
\frac{1}{x-4}-\frac{1}{x-3}=\frac{1}{{x}^{2}-7x+12}
Comparando con las opciones, concluimos que la correcta es la b).
Reactivo 9
Resuelva la siguiente ecuación.
\frac{1}{{x}^{2}-4}=\frac{5}{x+2}
- x=-\frac{11}{5}
- x=11
- x=\frac{11}{5}
- x=1
Solución:
Antes de comenzar a aplicar las propiedades de la igualdad, podemos ver que el denominador del miembro izquierdo puede factorizarse aplicando diferencia de cuadrados.
\frac{1}{{x}^{2}-4}=\frac{5}{x+2}\to \frac{1}{\left(x-2\right)\left(x+2\right)}=\frac{5}{x+2}
Ahora si es conveniente aplicar las propiedades de la igualdad, ya que el x+2 del primer miembro se cancela con el x+2 del segundo miembro.
\frac{1}{\left(x-2\right)\left(x+2\right)}=\frac{5}{x+2}\to \frac{1}{x-2}=5
Pasamos a multiplicar el denominador x-2 al segundo miembro.
1=5\left(x-2\right)\to 5x-10=1
Despejamos.
5x=1+10=11
\therefore x=\frac{11}{5}
La respuesta correcta es la opción c).
Reactivo 10
Calcule el valor de x que cumple la siguiente igualdad.
\frac{1}{x}+\frac{1}{2x+1}=2
- x=\frac{1+\sqrt{17}}{8}
- {x}_{1}=\frac{\sqrt{17}}{8}, {x}_{2}=\frac{-\sqrt{17}}{8}
- {x}_{1}=\frac{1+\sqrt{17}}{8}, {x}_{2}=\frac{1-\sqrt{17}}{8}
- {x}_{1}=1+\sqrt{17}, {x}_{2}=1-\sqrt{17}
Solución:
Para este problema, comencemos por eliminar los denominadores. Primero multiplicamos por x y luego por 2x+1 .
\frac{x}{x}+\frac{x}{2x+1}=2x\to 1+\frac{x}{2x+1}=2x
2x+1+\frac{x\left(2x+1\right)}{2x+1}=2x\left(2x+1\right)\to 2x+1+x=2x\left(2x+1\right)
Agrupamos y simplificamos.
3x+1=4{x}^{2}+2x\to 4{x}^{2}+2x-3x-1=0
4{x}^{2}-x-1=0
Ahora, aplicamos la fórmula de segundo grado.
{x}_{\mathrm{1,2}}=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}
Sustituimos los valores.
{x}_{\mathrm{1,2}}=\frac{1\pm \sqrt{{\left(-1\right)}^{2}-4\left(4\right)\left(-1\right)}}{2\left(4\right)}=\frac{1\pm \sqrt{1+16}}{8}=\frac{1\pm \sqrt{17}}{8}
Debido a que \sqrt{17} no posee raíz exacta, expresamos el resultado en forma de radical. Los valores que satisfacen la igualdad son:
{x}_{1}=\frac{1+\sqrt{17}}{8}, {x}_{2}=\frac{1-\sqrt{17}}{8}
Examinando los incisos, concluimos que la respuesta correcta es c).
Reactivo 11
Calcule el valor de x que satisface la siguiente ecuación logarítmica.
{\mathrm{log}}_{4}\left(x+1\right)-{\mathrm{log}}_{4}5={\mathrm{log}}_{4}\left(x-1\right)
- x=\frac{3}{2}
- x=\frac{1}{2}
- x=1
- x=2
Solución:
En el caso de las ecuaciones logarítmicas, debemos tener presentes las propiedades de la igualdad y de los logaritmos. Recordemos rápidamente las propiedades básicas sobre logaritmos.
- \mathrm{log}\left(a\cdot b\right)=\mathrm{log}\left(a\right)+\mathrm{log}\left(a\right)
- \mathrm{log}\left(\frac{a}{b}\right)=\mathrm{log}\left(a\right)-\mathrm{log}\left(a\right)
- \mathrm{log}\left({a}^{n}\right)=n\mathrm{log}\left(a\right)
- {\mathrm{log}}_{n}a=b\leftrightarrow {n}^{b}=a
Antes de decidir cuáles propiedades aplicar, agrupemos los logaritmos con x en un mismo miembro.
{\mathrm{log}}_{4}\left(x+1\right)-{\mathrm{log}}_{4}\left(x-1\right)={\mathrm{log}}_{4}5
Nos conviene aplicar la propiedad del logaritmo del cociente.
{\mathrm{log}}_{4}\left(x+1\right)-{\mathrm{log}}_{4}\left(x-1\right)={\mathrm{log}}_{4}5\to {\mathrm{log}}_{4}\left(\frac{x+1}{x-1}\right)={\mathrm{log}}_{4}5
Ahora, elevamos ambos miembros de la igualdad a la base del logaritmo, es decir, 4.
{4}^{{\mathrm{log}}_{4}\left(\frac{x+1}{x-1}\right)}={4}^{{\mathrm{log}}_{4}5}
Las bases cancelan a los logaritmos base 4.
\frac{x+1}{x-1}=5
En este punto, el problema se resume en resolver una ecuación lineal.
x+1=5\left(x-1\right)
x+1=5x-5\to 1+5=5x-x
4x=6\to x=\frac{3}{2}
Este resultado no es definitivo, ahora debemos sustituirlo en la igualdad original para determinar si se cumple o no.
{\mathrm{log}}_{4}\left(\frac{3}{2}+1\right)-{\mathrm{log}}_{4}5={\mathrm{log}}_{4}\left(\frac{3}{2}-1\right)
{\mathrm{log}}_{4}\left(\frac{5}{2}\right)-{\mathrm{log}}_{4}5={\mathrm{log}}_{4}\left(\frac{1}{2}\right)
Aplicamos la propiedad de la división en el primer miembro.
{\mathrm{log}}_{4}\left(\frac{5}{2}\right)-{\mathrm{log}}_{4}5={\mathrm{log}}_{4}\left(\frac{1}{2}\right)\to {\mathrm{log}}_{4}\left(\frac{\frac{5}{2}}{5}\right)={\mathrm{log}}_{4}\left(\frac{1}{2}\right)
Simplificando:
{\mathrm{log}}_{4}\left(\frac{1}{2}\right)={\mathrm{log}}_{4}\left(\frac{1}{2}\right)
Concluimos que x=\frac{3}{2} satisface la igualdad.
La respuesta correcta es la opción a).
Reactivo 12
A partir de las expresiones que se muestran en los incisos, determine cuál de ellas es la identidad.
- 0=\mathrm{sin}x
- x=\mathrm{sin}x
- {x}^{2}+x=3
- {\mathrm{sin}}^{2}x+{\mathrm{cos}}^{2}x=1
Solución:
Para responder esta pregunta, debemos entender la diferencia entre igualdad e identidad. En matemáticas, una igualdad es aquella que se establece entre dos objetos matemáticos que coinciden para un conjunto finito de valores de la variable independiente.
Teniendo en cuenta lo anterior, sabemos que son igualdades el a), el b) y el c); porque sólo en determinados valores de x se cumple la asignación hecha entre los miembros.
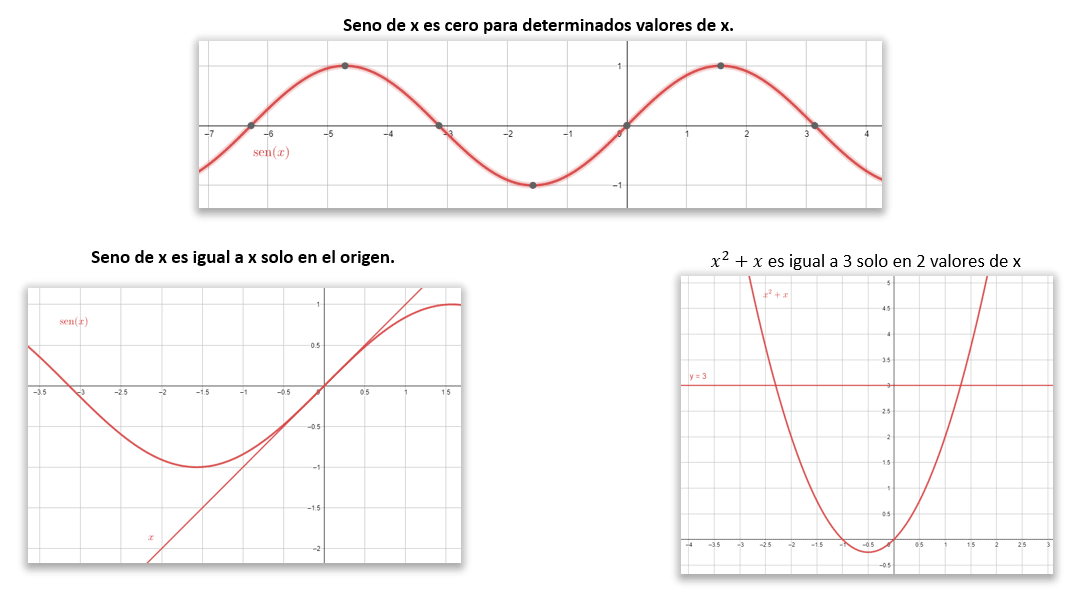
Por otro lado, las identidades son igualdades que se establecen entre dos objetos matemáticos que siempre coinciden. Para cualquier valor de la variable independiente, ambos miembros tienen el mismo valor. El único que cumple con esto es la conocida identidad pitagórica.
{\mathrm{sin}}^{2}x+{\mathrm{cos}}^{2}x=1

Concluimos que la respuesta correcta es el inciso d).
Reactivo 13
Calcule el valor de la siguiente desigualdad lineal.
\frac{3x+1}{2}\ge 2x-1
- x\ge 3
- x\le 3
- x\in \left\{R\right\}
- x \in \left(-3, 3\right)
Solución:
A la hora de resolver inecuaciones lineales, debemos tener presente las propiedades de las desigualdades. Son bastante parecidas a las igualdades, pero una de las principales diferencias es que: si multiplicamos o dividimos por un número negativo, la desigualdad cambia de dirección.
Comencemos por multiplicar ambos miembros por +2. Es positivo, por tanto, se mantiene el sentido de la desigualdad.
2\left(\frac{3x+1}{2}\right)\ge 2\left(2x-1\right)
3x+1\ge 4x-2
Agrupamos los términos con x a la izquierda.
3x-4x\ge -1-2
-x\ge -3
Para eliminar el signo negativo de la x multiplicamos ambos miembros por -1. Cambia el sentido de la desigualdad.
\therefore x\le 3
El conjunto solución de la desigualdad son todos los reales menores o iguales que 3.
La respuesta correcta es el inciso b).
Reactivo 14
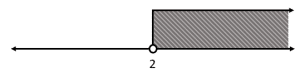
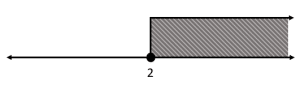
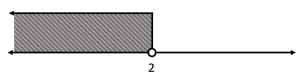
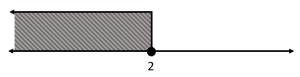
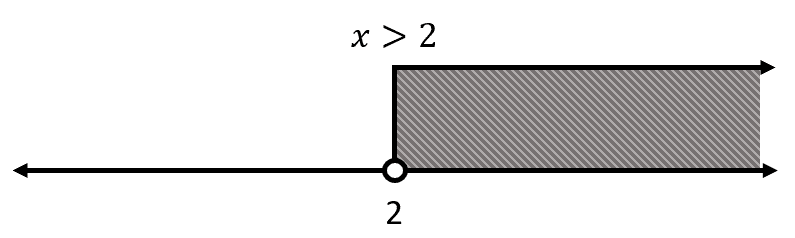
Indique cuál de las siguientes gráficas representa correctamente la desigualdad x>2 .
Solución:
Para seleccionar la respuesta correcta, debemos tener presente las dos principales reglas para representar gráficamente a las desigualdades:
- Se dibuja una flecha que apunta en la dirección de la desigualdad
- Para indicar que un extremo es abierto o cerrado, se coloca un punto vacío o relleno respectivamente
Examinando la desigualdad del enunciado, se trata de un mayor que con extremo inicial en +2 abierto. Si fuera mayor o igual que, el extremo sería cerrado. La flecha debe apuntar hacia la derecha, en sentido a +\infty .
Teniendo en cuenta el análisis anterior, el inciso que concuerda es el a).
Reactivo 15
Calcule el conjunto de valores que satisfacen la inecuación:
2x-1<x+4
- \left(5, \infty \right)
- \left[-\infty , 5\right]
- \left(-\infty , -5\right)
- \left(-\infty , 5\right)
Solución:
Comenzamos agrupando los términos con x al primer miembro y los independientes al segundo.
2x-x<1+4
Resolvemos las operaciones indicadas.
x<5
El conjunto solución de la inecuación son todos los valores de x que pertenecen a \left(-\infty , 5\right) .
La respuesta correcta es el inciso d).
Reactivo 16
Determine el conjunto de valores que satisface la siguiente desigualdad.
\frac{x+1}{x-1}\le 0
- \left(-\infty , 1\right]
- \left[-1, 1\right)
- \left(-1, 1\right)
- \left[-1, \infty \right)
Solución:
Para calcular el conjunto solución de esta desigualdad, no podemos despejar el denominador al segundo miembro y resolver con el numerador. Esto sería un error, porque solo estaríamos calculando el valor que anula a la fracción.
En estos casos, debemos estudiar qué valores del numerador y del denominador hacen a la fracción negativa o cero. Recordando la ley de signos para las divisiones, el resultado es negativo cuando:
- El numerador es positivo y el denominador es negativo
- El numerador es negativo y el denominador es positivo
Además, la fracción es igual a cero sólo cuando el numerador se anula. Expresando todo lo anterior en desigualdad nos queda:
Caso 1: El numerador es positivo o igual a cero y el denominador es negativo.
x+1\ge 0\wedge x-1<0
Caso 2: El numerador es negativo o igual a cero y el denominador es positivo.
x+1\le 0\wedge x-1>0
El resultado general de la inecuación, será la unión de los resultados parciales de los casos 1 y 2.
Caso 1.
x+1\ge 0\to x\ge -1
x-1<0\to x<1
Interceptamos ambas soluciones:
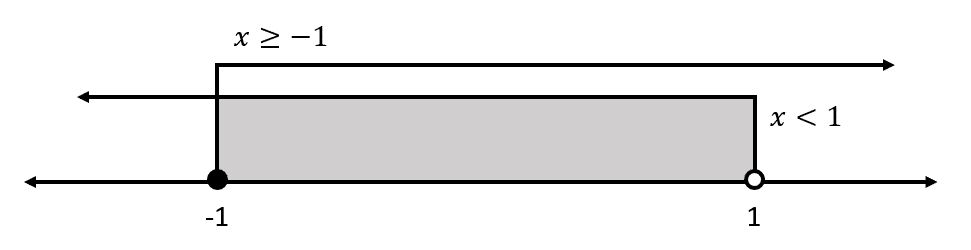
So{l}_{1}=x\in \left[-1, 1\right)
Caso 2.
x+1\le 0\to x\le -1
x-1>0\to x>1
Interceptamos ambas soluciones:
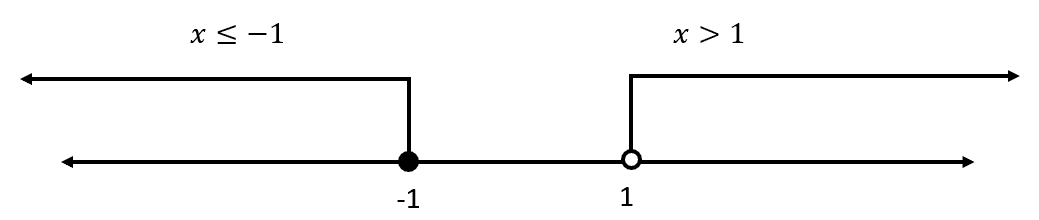
Debido a que no se interceptan, la solución 2 es el conjunto vacío.
So{l}_{2}=\left\{\varnothing \right\}
Uniendo ambas soluciones nos queda:
Sol=\left\{\varnothing \right\}\cup \left[-1, 1\right)=\left[-1, 1\right)
El conjunto solución de la inecuación es todo valor de x entre -1 incluido hasta 1.
Comparando, nos queda seleccionar la opción b) como correcta.
Reactivo 17
Determine los valores de x y y que satisfacen las ecuaciones indicadas a continuación aplicando el método por sustitución.
\left\{\begin{array}{c}5x+9y=-\frac{11}{2}\\ 16x-9y=-5\end{array}\right.
- x=-\frac{1}{2}, y=-\frac{1}{3}
- x=\frac{1}{2}, y=\frac{1}{3}
- x=-2, y=-3
- x=2, y=3
Solución:
El método de solución por sustitución, consiste en seleccionar una de las ecuaciones y despejar una de las variables del sistema, para luego sustituir la expresión resultante en la otra ecuación.
Una recomendación general a la hora de resolver SEL, es intentar eliminar las fracciones. La primera ecuación tiene al término independiente en forma de fracción, multipliquemos ambos miembros por 2 para simplificar.
\left\{\begin{array}{c}10x+18y=-11\\ 16x-9y=-5\end{array}\right.
Ahora, nos queda seleccionar una de las ecuaciones y variables para despejar. Esta vez será la variable x en la primera ecuación.
{I}_{1}: 10x+18y=-11\to 10x=-11-18y
x=-\frac{18y+11}{10}
Sustituimos esta expresión en la segunda ecuación.
16\left(-\frac{18y+11}{10}\right)-9y=-5
Multiplicamos toda la ecuación por -10.
16\left(18y+11\right)+90y=50
Dividimos entre 2 y simplificamos.
8\left(18y+11\right)+45y=25
144y+88+45y=25
189y=25-88\to 189y=-63
\therefore y=-\frac{1}{3}
Sustituimos este resultado en x=-\frac{18y+11}{10} para obtener a x .
x=-\frac{18\left(-\frac{1}{3}\right)+11}{10}=-\frac{1}{2}
Los valores que resuelven el SEL son:
x=-\frac{1}{2}, y=-\frac{1}{3}
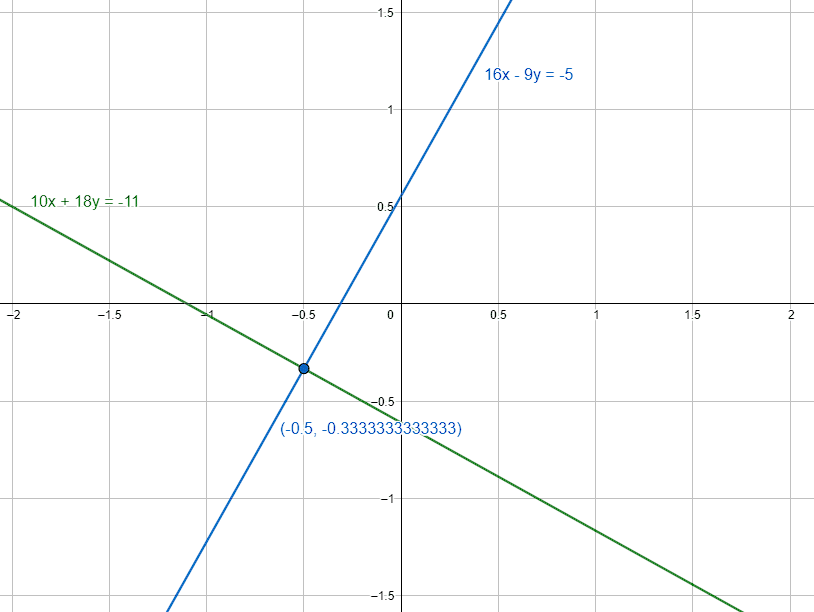
Respuesta correcta: inciso a).
Reactivo 18
Calcule el punto de intersección de las rectas x+y=2 y -2x+y=1 , empleando el método por igualación.
- \left(-\frac{1}{3},-\frac{5}{3}\right)
- \left(-\frac{1}{3},\frac{5}{3}\right)
- \left(\mathrm{1,3}\right)
- \left(\frac{1}{3},\frac{5}{3}\right)
Solución:
En otras palabras, el enunciado nos pide que resolvamos el sistema de ecuaciones formado por las ecuaciones de las rectas.
\left\{\begin{array}{c}x+y=2\\ -2x+y=1\end{array}\right.
El método por igualación, consiste en seleccionar una de las variables y despejar de ambas ecuaciones. Las expresiones resultantes se igualan para resolver el SEL. En este caso, seleccionamos a la variable y , ya que es la más sencilla de despejar.
Ecuación 1.
x+y=2\to y=2-x
Ecuación 2.
-2x+y=1\to y=1+2x
Igualamos las expresiones.
y=y\to 2-x=1+2x
Despejamos.
2-1=x+2x\to 3x=1
\therefore x=\frac{1}{3}
Sustituimos este resultado en cualquiera de los despejes de y .
y=2-\frac{1}{3}=\frac{5}{3}
El punto de intersección de las dos rectas es:
\left(x,y\right)=\left(\frac{1}{3},\frac{5}{3}\right)
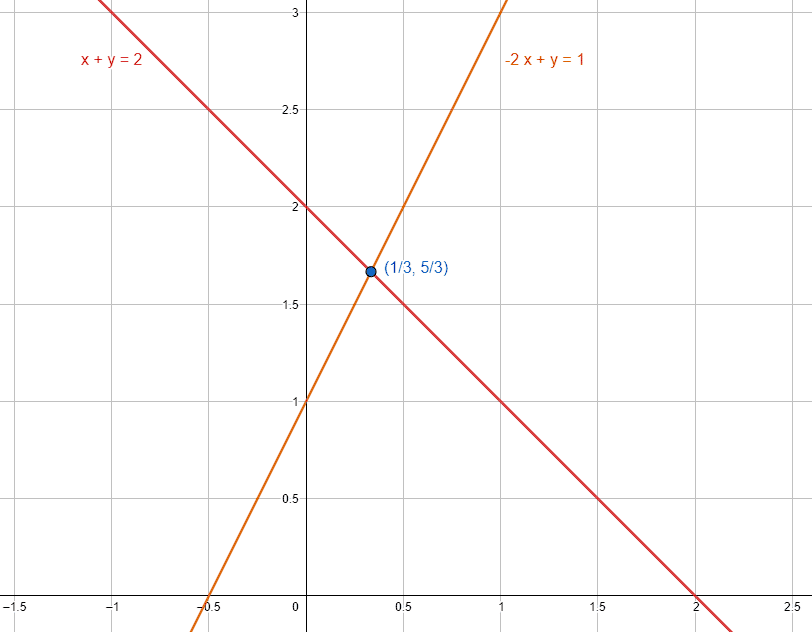
La respuesta correcta es el inciso d).
Reactivo 19
Calcule los valores de x y de y que satisfacen el siguiente sistema de ecuaciones, empleando el método por reducción.
\left\{\begin{array}{c}10x-3y=36\\ 2x+5y=-4\end{array}\right.
- x=-2, y=3
- x=3, y=2
- x=3, y=-2
- x=-3, y=-2
Solución:
El método por reducción permite eliminar una de las incógnitas del sistema, multiplicando a una de las ecuaciones por una constante y luego sumándole con la otra para cancelar a la variable objetivo.
¿Cómo determinar la constante en el método por reducción? Debemos examinar cuál de las variables tienen coeficientes con cociente entero. Dividimos el mayor sobre el menor y el resultado lo multiplicamos por el menor pero cambiado de signo.
Si ninguna de las incógnitas posee coeficientes con cociente entero, se escoge cualquiera de las dos. En este caso, la variable con coeficientes de cociente entero es x , ya que: \frac{10}{2}=5 . Multiplicamos la ecuación 2 por -5.
\left\{\begin{array}{c}10x-3y=36\\ -10x-25y=20\end{array}\right.
Sumamos las expresiones.
\begin{array}{c}10x-3y=36\\ -10x-25y=20\end{array}
0-28y=56
Despejamos el valor de y .
y=-2
Sustituimos en una de las ecuaciones y despejamos a x .
10x-3\left(-2\right)=36\to 10x+6=36
\therefore x=3
Los valores de x y y que satisfacen al SEL son:
x=3, y=-2
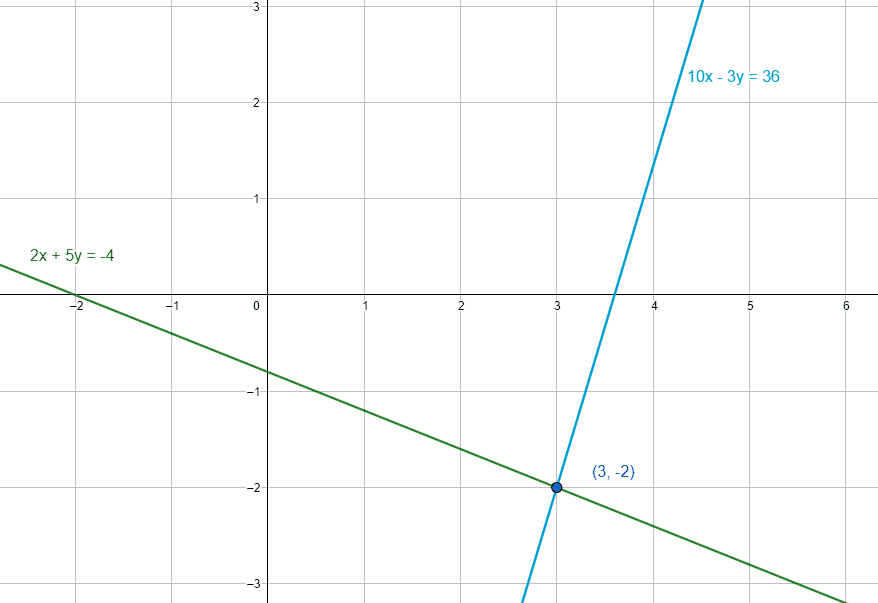
Comparando con las opciones, la respuesta correcta es la c).
Reactivo 20
A partir de las rectas que se muestran en la figura, determine gráficamente su intersección. Tenga en cuenta que cada casilla mide 1 unidad.
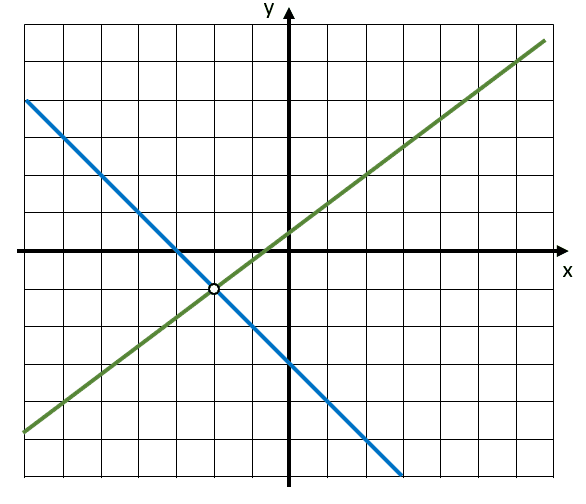
- \left(-2, -1\right)
- \left(2, -1\right)
- \left(-2, 1\right)
- \left(-1, -2\right)
Solución:
El método de solución para este caso es el gráfico. Determinar la ecuación de cada recta y luego resolver el SEL sería un derroche de tiempo, ya que la gráfica muestra claramente la intersección de las rectas y conocemos la distancia de cada casilla.
Teniendo esto en cuenta, las coordenadas del punto son: -2 en x y -1 en y .
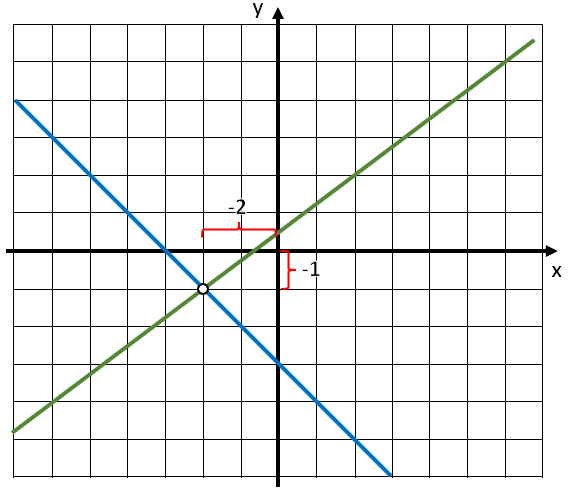
Intersección de las rectas:
\left(x, y\right)=\left(-2, -1\right)
La respuesta correcta es la opción a).
Reactivo 21
Calcule el valor que debería tener z en el sistema de ecuaciones 3×3, empleando el método más oportuno.
\left\{\begin{array}{c}3x-2y+3z=6\\ 4x+3y-2z=10\\ 5x+7y+5z=7\end{array}\right.
- z=\frac{113}{186}
- z=\frac{-113}{186}
- z=113
- z=-113
Solución:
La regla de Cramer es un método para resolver sistemas de ecuaciones, basado en determinantes de matrices. La misma nos dice que:
El valor de cualquiera de las variables del sistema de ecuaciones lineales cuadrado, es igual al cociente del determinante de la incógnita entre el determinante del sistema.
x=\frac{{\mathrm{\Delta }}_{x}}{{\mathrm{\Delta }}_{s}}, y=\frac{{\mathrm{\Delta }}_{y}}{{\mathrm{\Delta }}_{s}}, z=\frac{{\mathrm{\Delta }}_{z}}{{\mathrm{\Delta }}_{s}}
Comenzamos por calcular el determinante del sistema, formado por los coeficientes de las variables.
{\mathrm{\Delta }}_{s}=\left|\begin{array}{ccc}3& -2& 3\\ 4& 3& -2\\ 5& 7& 5\end{array}\right|=3\left|\begin{array}{cc}3& -2\\ 7& 5\end{array}\right|-\left(-2\right)\left|\begin{array}{cc}4& -2\\ 5& 5\end{array}\right|+3\left|\begin{array}{cc}4& 3\\ 5& 7\end{array}\right|
{\mathrm{\Delta }}_{s}=3\left(15+14\right)+2\left(20+10\right)+3\left(28-15\right)
{\mathrm{\Delta }}_{s}=3\left(29\right)+2\left(30\right)+3\left(13\right)
{\mathrm{\Delta }}_{s}=186
Ahora, calculamos el determinante para z . Por esto, la regla de Cramer es el método más oportuno. La matriz de z , es igual a la del sistema, pero sustituyendo la columna de z por los términos independientes.
{\mathrm{\Delta }}_{z}=\left|\begin{array}{ccc}3& -2& 6\\ 4& 3& 10\\ 5& 7& 7\end{array}\right|=3\left|\begin{array}{cc}3& 10\\ 7& 7\end{array}\right|-\left(-2\right)\left|\begin{array}{cc}4& 10\\ 5& 7\end{array}\right|+6\left|\begin{array}{cc}4& 3\\ 5& 7\end{array}\right|
{\mathrm{\Delta }}_{z}=3\left(21-70\right)+2\left(28-50\right)+6\left(28-15\right)
{\mathrm{\Delta }}_{z}=3\left(-49\right)+2\left(-22\right)+6\left(13\right)
{\mathrm{\Delta }}_{z}=-113
Finalmente, calculamos el valor de z como:
z=\frac{-113}{186}\approx -0.6075
Concluimos indicando que la respuesta correcta es el inciso b).
Reactivo 22
Calcule el dominio de la función f\left(x\right)=\sqrt{x+1} .
- \left[1, \infty \right)
- \left[-1, \infty \right)
- \left[-1, 1\right)
- \left(-1, \infty \right)
Solución:
Para determinar el dominio de cualquier función, debemos tener en cuenta dos cosas:
- Las restricciones de las funciones elementales que componen a f\left(x\right)
- Que el dominio total será la intersección de las soluciones para las funciones elementales
En este caso, f\left(x\right) es una función radical de índice par ( n=2 ), cuya restricción es que su radicando sea mayor o igual que 0. El radicando es x+1 , por tanto:
\mathrm{D}\mathrm{o}\mathrm{m}\left(f\right)=\left\{x\right|x+1\ge 0\}
Resolvemos la inecuación lineal para encontrar el conjunto solución.
x+1\ge 0\to x\ge -1
El dominio de f son todos los reales mayores o iguales que 1. Escrito en notación de intervalo:
\mathrm{D}\mathrm{o}\mathrm{m}\left(f\right)=\left\{x | x\in \left[-1, \infty \right)\right\}

La respuesta correcta es el inciso b).
Reactivo 23
Si una función f\left(x\right) es polinómica de grado n , ¿qué se puede inferir acerca de su dominio?
- Lo conforman todos los puntos que satisfacen a f\left(x\right)=0
- Depende de los puntos críticos de la función
- Está compuesto por todos los números reales
- El dominio depende de los coeficientes del polinomio
Solución:
Las funciones polinómicas o algebraicas, son aquellas con regla de correspondencia igual a un polinomio, es decir:
f\left(x\right)={a}_{n}{x}^{n}+{a}_{n-1}{x}^{n-1}+\dots +{a}_{1}x+{a}_{0}
Su principal característica es que no presentan indeterminaciones o discontinuidades para cualquier valor de x , por tanto, su gráfica es una curva continua sobre el plano cartesiano. Como consecuencia a esto último, el dominio de cualquier función polinómica son todos los reales.
\mathrm{D}\mathrm{o}\mathrm{m}\left(f\right)=\left\{R\right\}
Examinando los incisos, concluimos que la respuesta correcta es el c): Está compuesto por todos los números reales.
Reactivo 24
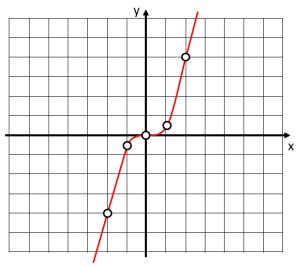
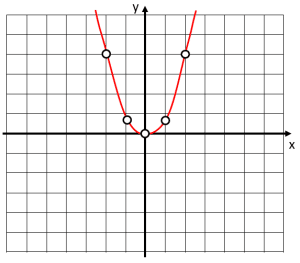
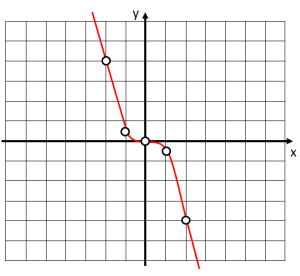
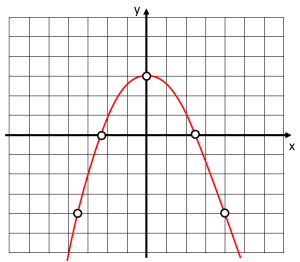
Identifique el gráfico para la función g\left(x\right)={x}^{3} , a partir de los siguientes valores de x .

Solución:
Para seleccionar la gráfica que representa correctamente a la función g\left(x\right)={x}^{3} , debemos empezar por calcular la imagen que tendrían los puntos de x indicados en la tabla.
Sustituyendo en la función cada valor nos queda:

Lo primero que podemos observar, es que la gráfica de la función tiene valores en el primer y tercer cuadrante. La única opción que cumple con esta característica, es la a).
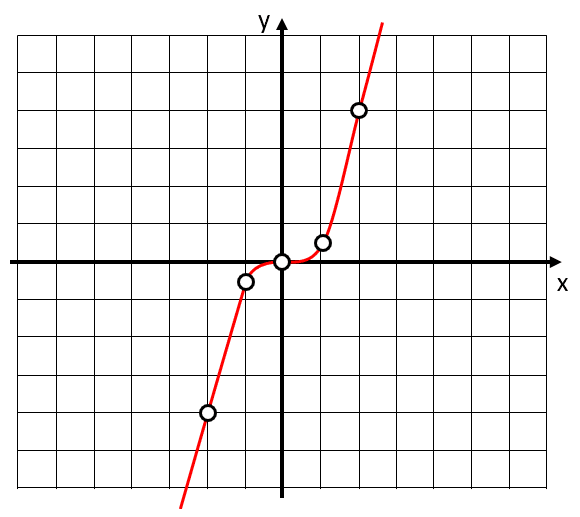
Comprobamos rápidamente que los valores concuerden.
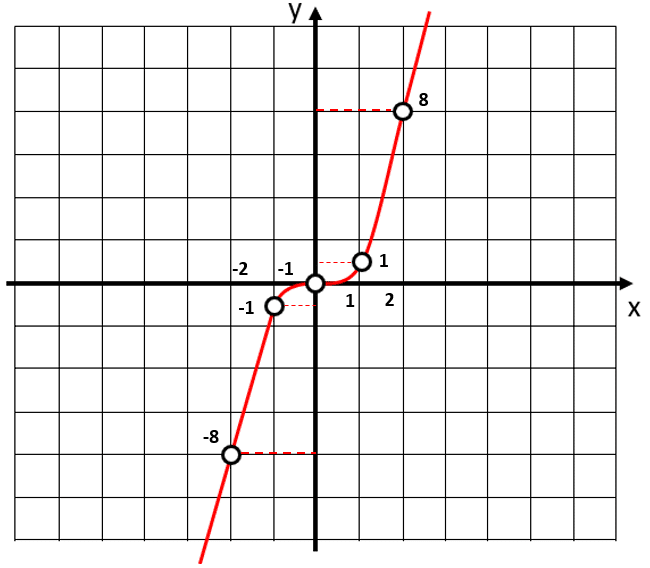
La respuesta correcta es el inciso a).
Reactivo 25
Calcule el dominio de la siguiente función:
f\left(x\right)=\frac{\left|x\right|}{\sqrt{4-{x}^{2}}}
- x\in \left(-2, 2\right)
- x\in \left(-2, \infty \right)
- x\in \left(-\infty , 2\right)
- x\in \left[-2, 2\right]
Solución:
Aunque la función parezca intimidante, en cualquier caso, siempre debemos identificar el tipo de función principal y luego establecer las restricciones para que la misma exista. La función es de tipo racional y su única restricción es que el denominador sea diferente de cero.
\sqrt{4-{x}^{2}}\ne 0
Ya no es necesario incluir en el estudio la función valor absoluto del numerador. Por otra parte, los radicales tienen su propia restricción: que el radicando sea mayor o igual que cero.
4-{x}^{2}\ge 0
Debido a que no puede ser cero por la restricción anterior, solo consideramos los valores que hacen al radicando mayor que cero.
4-{x}^{2}>0
Factorizamos la diferencia de cuadrados.
\left(2-x\right)\left(2+x\right)>0
El producto será positivo cuando: ambos sean negativos o cuando ambos sean positivos.
Ambos son positivos:
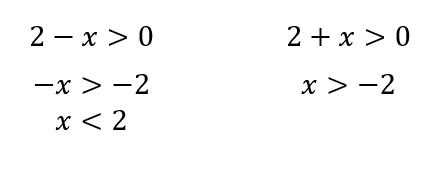
Interceptando las soluciones nos queda:
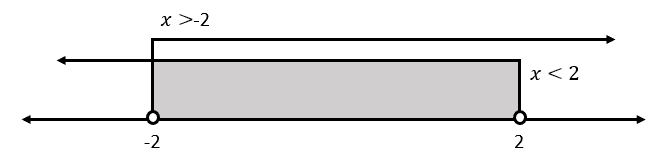
So{l}_{1}=x\in \left(-2, 2\right)
Ambos son negativos:
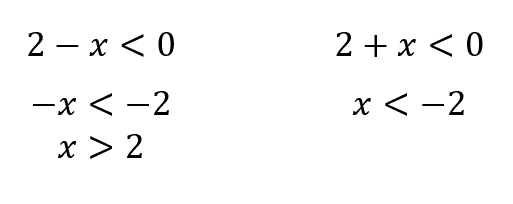
Interceptando las soluciones:
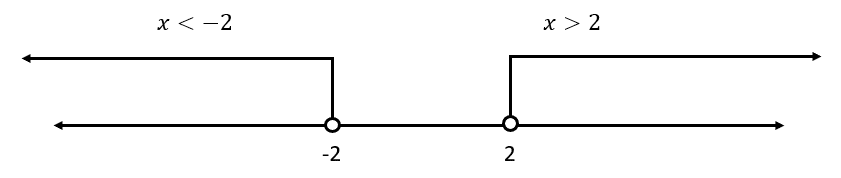
So{l}_{2}=\left\{\varnothing \right\}
Uniendo ambas soluciones concluimos que el dominio de la función es:
\mathrm{D}\mathrm{o}\mathrm{m}\left\{f\right\}=x\in \left(-2, 2\right)
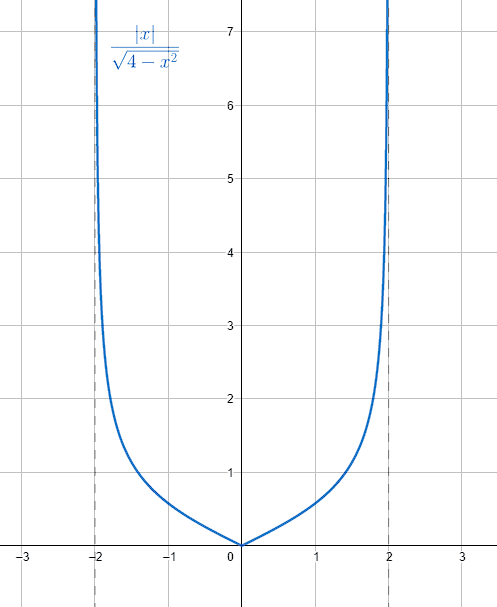
Vemos en la gráfica que la función existe en dentro de -2 y 2.
La respuesta correcta es el inciso a).
Reactivo 26
¿Cuánto es \frac{\pi }{6} radianes en grados sexagesimales?
- 15°
- 20°
- 25°
- 30°
Solución:
Para convertir de grados a radianes y viceversa, utilizamos la siguiente identidad:
180°=\pi
Ya que necesitamos el resultado en grados, multiplicamos \frac{\pi }{6} por 180° y luego dividimos por \pi .
x=\frac{\pi }{6}\cdot \frac{180°}{\pi }=30°
\frac{\pi }{6} es igual a 30 grados sexagesimales.
La respuesta correcta es el inciso d).
Reactivo 27
Calcule la x en el triángulo rectángulo de la figura, a partir de los datos suministrados.
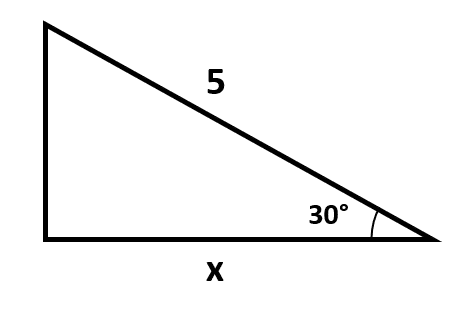
- 4 \mathrm{m}
- 4.33 \mathrm{m}
- 3 \mathrm{m}
- 2.5 \mathrm{m}
Solución:
Para calcular el valor de x en el triángulo rectángulo, debemos emplear una de las identidades trigonométricas elementales. Si nos posicionamos sobre el ángulo de 30°, veremos que el cateto adyacente es x , debemos emplear el coseno de 30° .
\mathrm{cos}30°=\frac{CA}{H}=\frac{x}{5}
Despejamos a x .
x=5\mathrm{cos}30°
Sustituyendo \mathrm{cos}30°=0.8660 nos queda:
x=5\left(0.8660\right)=4.33
El lado x mide 4.33 unidades métricas.
La respuesta correcta es el inciso b).
Reactivo 28
Calcule el valor del ángulo indicado con x , en el triángulo que se muestra a continuación.
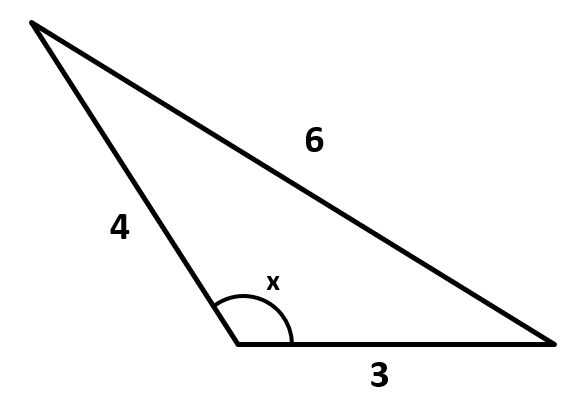
- 62.72°
- 117.28°
- 180°
- 128°
Solución:
La ley del coseno es una relación para triángulos obtusángulos, que relaciona los tres lados y un ángulo opuesto a uno de los lados.
{a}^{2}={b}^{2}+{c}^{2}-2bc\mathrm{cos}x
Donde a es el lado opuesto al ángulo x .
En este caso, el valor del ángulo es desconocido y el lado opuesto a x es el que mide 6 unidades. Sustituimos:
{6}^{2}={3}^{2}+{4}^{2}-2\left(3\right)\left(4\right)\mathrm{cos}x
Despejamos al coseno de x .
\mathrm{cos}x=\frac{{6}^{2}-{3}^{2}-{4}^{2}}{-24}
Simplificamos:
\mathrm{cos}x=-\frac{11}{24}=-0.4583
Aplicamos coseno inverso para despejar a la x .
x={\mathrm{cos}}^{-1}\left(-0.4583\right)\approx 117.28°
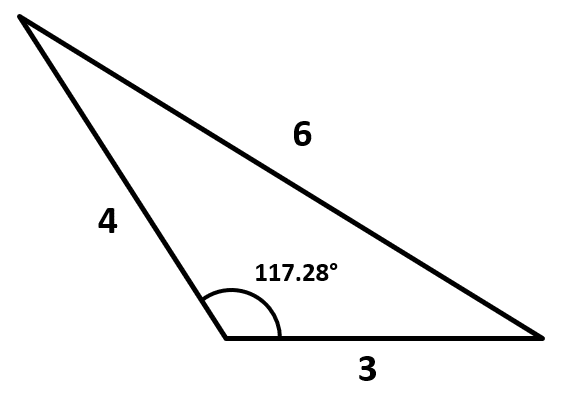
Concluimos seleccionando la opción b) como correcta.
Reactivo 29
Calcule el seno del ángulo indicado dentro de la circunferencia trigonométrica.
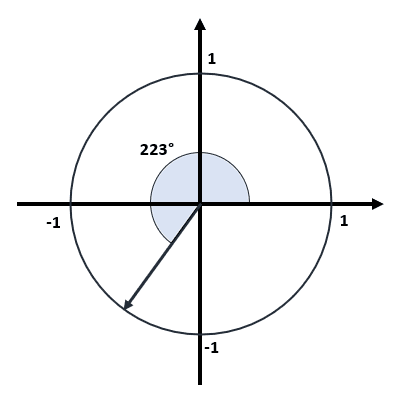
- -0.682
- 0.682
- -0.802
- 0.802
Solución:
Cuando el ángulo se encuentra en el tercer cuadrante, debemos restarle 180° para trabajar con la porción del ángulo entre la línea de 180° y la flecha.
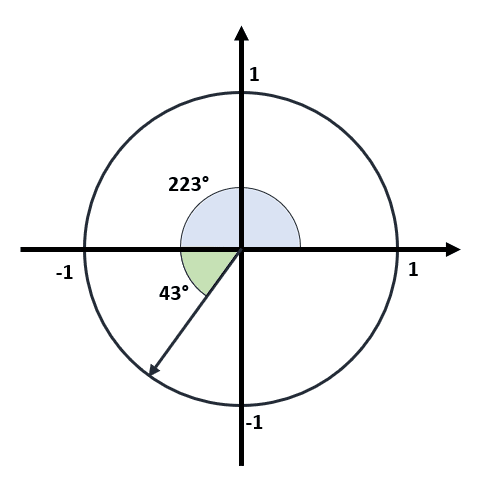
Luego, determinamos el signo que debe tener el seno en el tercer cuadrante, calculamos el seno de 43° y al resultado le colocamos el signo antes mencionado.
Para el tercer cuadrante el seno es negativo. El seno de 43° es igual a:
\mathrm{sin}43°=0.682
El resultado para el seno de 223° es el resultado anterior con signo negativo.
\mathrm{sin}223°=-0.682
La respuesta correcta es el inciso a).
Reactivo 30
Identifique a cuál de las siguientes identidades, es equivalente la expresión:
\frac{\mathrm{cos}x}{1+\mathrm{sin}x}
- \mathrm{sec}x+\mathrm{tan}x
- \mathrm{sec}x-\mathrm{tan}x
- \mathrm{sec}x-\mathrm{cot}x
- \mathrm{csc}x+\mathrm{tan}x
Solución:
Examinando la expresión, ninguna de las identidades elementales corresponde al numerador o al denominador. Pero podemos multiplicar y dividir por 1-\mathrm{sin}x para aplicar luego la identidad pitagórica.
\frac{\mathrm{cos}x\left(1-\mathrm{sin}x\right)}{\left(1+\mathrm{sin}x\right)\left(1-\mathrm{sin}x\right)}=\frac{\mathrm{cos}x\left(1-\mathrm{sin}x\right)}{1-{\mathrm{sin}}^{2}x}
Sustituimos 1-{\mathrm{sin}}^{2}x por {\mathrm{cos}}^{2}x .
=\frac{\mathrm{cos}x\left(1-\mathrm{sin}x\right)}{{\mathrm{cos}}^{2}x}
Simplificamos.
=\frac{1-\mathrm{sin}x}{\mathrm{cos}x}=\frac{1}{\mathrm{cos}x}-\frac{\mathrm{sin}x}{\mathrm{cos}x}
Aplicamos la identidad de la secante y la tangente.
=\mathrm{sec}x-\mathrm{tan}x
Finalmente:
\frac{\mathrm{cos}x}{1+\mathrm{sin}x}=\mathrm{sec}x-\mathrm{tan}x
Hacemos una rápida comprobación gráfica en Geogebra.
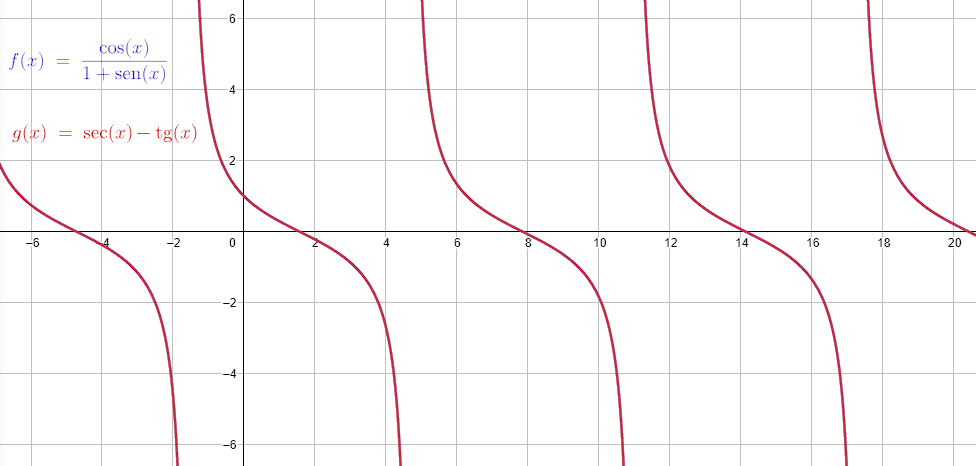
Las gráficas se solapan mutuamente.
La respuesta correcta es el inciso b).