Seguimos con la segunda parte de este examen simulacro de matemáticas para el área 1 de la UNAM. Vamos con los últimos 13 reactivos.

Instrucciones
A continuación encontrarás un examen simulado diseñado para evaluar tus conocimientos. Por favor, lee atentamente las siguientes instrucciones antes de comenzar:
- Tienes dos minutos por pregunta.
- Solo puedes elegir la respuesta que consideres correcta una vez.
- Al elegir la respuesta, podrás ver la explicación del ejercicio.
- Al finalizar, podrás obtener tus resultados.
Te recomiendo que no mires las respuestas hasta que termines el examen, esto para que no pierdas tiempo y trates de “simular” que estás haciendo el examen real.
Reactivo 14: Distancia entre un punto y una recta
La distancia del punto \left(-\mathrm{1,1}\right) a la recta dada por la ecuación -3x+4y-8=0 es:
Solución:
En geometría Euclidiana, cuando hablamos de distancia entre elementos nos referimos a la distancia más corta entre ellos. Para la situación planteada en el problema, la distancia más corta es la que se haya trazando un segmento perpendicular desde la recta hasta el punto.
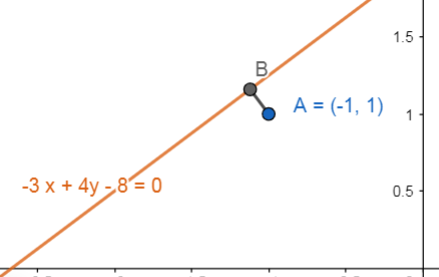
La magnitud de la distancia puede calcularse mediante la siguiente ecuación:
d=\left|\frac{A{x}_{p}+B{y}_{p}+C}{\sqrt{{A}^{2}+{B}^{2}}}\right|
Donde A , B y C son los coeficientes de la recta y {x}_{p}, {y}_{p} las coordenadas del punto. Sustituimos.
d=\left|\frac{-3\left(-1\right)+4\left(1\right)-8}{\sqrt{{\left(-3\right)}^{2}+{\left(4\right)}^{2}}}\right|=\left|\frac{3+4-8}{\sqrt{9+16}}\right|=\left|\frac{-1}{\sqrt{25}}\right|=\left|\frac{-1}{5}\right|
Eliminamos las barras de valor absoluto escribiendo a la cantidad interior positiva.
d=\left|\frac{-1}{5}\right|=\frac{1}{5}=0.2
La distancia entre el punto y la recta es de 0.2 unidades.
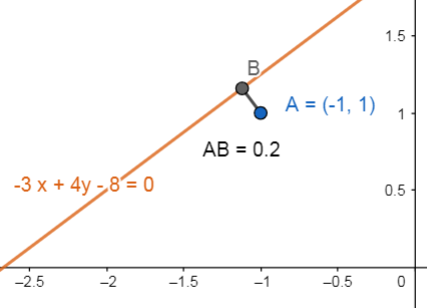
Comparando con las opciones, seleccionamos como correcta la A.
Reactivo 15: Problemas de distancia
En un marco de referencia representado por un plano XY , se localiza un gasoducto sobre la recta 3x+4y=2 con una fábrica en el punto \left(6, 6\right) . ¿Qué longitud, en metros, se requiere para conectar perpendicularmente a la fábrica con el gasoducto?
Solución:
Hagamos un rápido bosquejo de la situación planteada por el enunciado del problema.
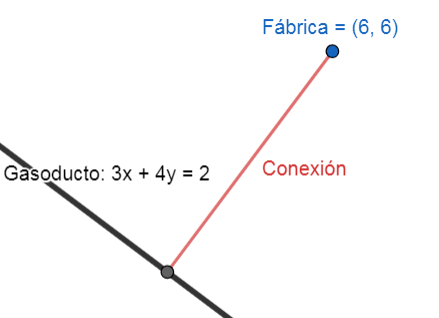
Ya que nos piden la distancia perpendicular entre el punto y la recta, el problema se resume en la fórmula de distancia entre una recta y un punto.
d=\left|\frac{A{x}_{p}+B{y}_{p}+C}{\sqrt{{A}^{2}+{B}^{2}}}\right|
La ecuación de la recta debe estar en su forma ordinaria, pasamos al primer miembro el 2.
l:3x+4y-2=0
P\left(6, 6\right)
Sustituimos.
d=\left|\frac{3\left(6\right)+4\left(6\right)-2}{\sqrt{{\left(3\right)}^{2}+{\left(4\right)}^{2}}}\right|=\left|\frac{40}{\sqrt{25}}\right|=\left|\frac{40}{5}\right|=8
El ducto de conexión debe medir 8 metros.
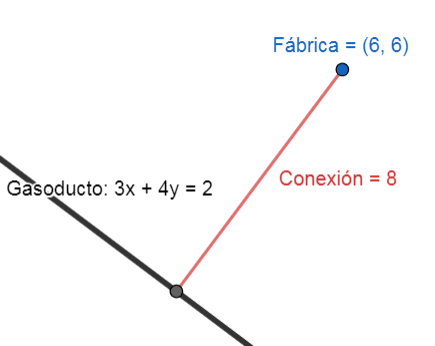
Concluimos seleccionando como correcta la opción C.
Reactivo 16: Centro de la circunferencia
Indica las coordenadas del centro de la circunferencia cuya ecuación general es 3{x}^{2}+3{y}^{2}+12x-30y+6=0
Solución:
Para encontrar las coordenadas del centro de la circunferencia, debemos aplicar completación de cuadrados a la ecuación en forma general, comencemos por la variable x .
Dividimos entre 3 toda la ecuación.
{x}^{2}+{y}^{2}+4x-10y+2=0
Agrupamos los términos con x .
{x}^{2}+4x+{y}^{2}-10y+2=0
Para completar cuadrados en x , sumamos y restamos 4.
{x}^{2}+4x+4+{y}^{2}-10y+2-4=0
{x}^{2}+4x+4+{y}^{2}-10y-2=0
Los términos {x}^{2}+4x+4 pueden escribirse como {\left(x+2\right)}^{2} .
{\left(x+2\right)}^{2}+{y}^{2}-10y-2=0
Para completar cuadrados en y , sumamos y restamos 25.
{\left(x+2\right)}^{2}+{y}^{2}-10y+25-2-25=0
{\left(x+2\right)}^{2}+{y}^{2}-10y+25-27=0
Los términos {y}^{2}-10y+25 pueden reescribirse como {\left(y-5\right)}^{2} .
{\left(x+2\right)}^{2}+{\left(y-5\right)}^{2}-27=0
{\left(x+2\right)}^{2}+{\left(y-5\right)}^{2}=27
Con la circunferencia en su forma ordinaria, extraemos por simple inspección las coordenadas del centro.
C\left(-\mathrm{2,5}\right)
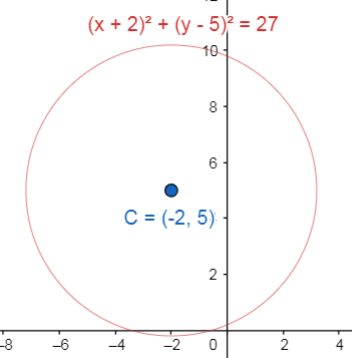
Finalmente, indicamos la opción B como respuesta correcta.
Reactivo 17: Ecuación de la parábola
Selecciona la ecuación de la parábola con foco F\left(\mathrm{1,0}\right) , valor del parámetro P=1 y eje focal paralelo al eje x .
Solución:
La ecuación de una parábola con vértice en un punto \left(h,k\right) y con eje focal paralelo a las x es:
{\left(y-k\right)}^{2}=4p\left(x-h\right)
Tenemos el valor de P=1 que además, nos dice que la parábola abre hacia la derecha. Por otro lado, no conocemos las coordenadas del vértice, pero sí las del foco.
Como la parábola tiene el eje focal paralelo a las x , el vértice y el foco tienen la misma coordenada en y . Además, el vértice debe encontrarse detrás del foco, exactamente a -P unidades. En base a esto, las coordenadas del vértice son:
V=\left(1-P,0\right)=\left(1-\mathrm{1,0}\right)=\left(\mathrm{0,0}\right)
La parábola tiene vértice en el origen. Sustituimos.
{\left(y-0\right)}^{2}=4\left(1\right)\left(x-0\right)\to {y}^{2}=4x
\therefore {y}^{2}-4x=0
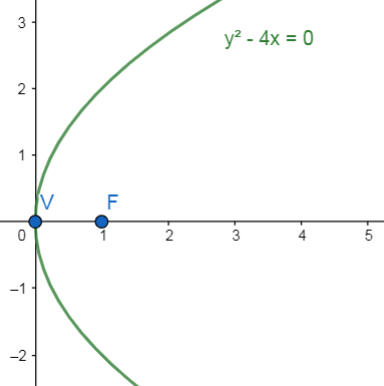
Concluimos seleccionando como respuesta correcta al inciso C.
Reactivo 18: Lugares geométricos y cónicas
Lugar geométrico en el plano de un punto cualquiera, que la suma de las distancias a dos puntos fijos llamados focos, es una cantidad constante.
Solución:
Recordemos la definición de elipse:
La elipse, es el lugar geométrico descrito por un punto P\left(x,y\right) donde la suma de las distancias respecto a otros dos puntos fijos llamados focos, es constante.
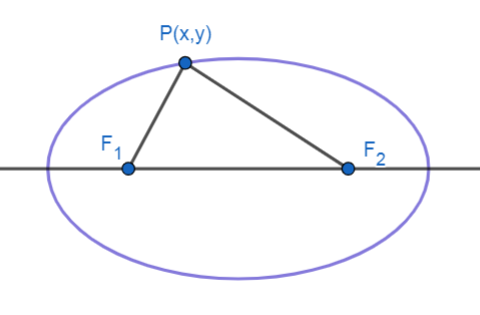
Si comparamos con lo enunciado en el problema, ambas definiciones describen al mismo lugar geométrico, por tanto, la respuesta correcta es la A Elipse.
Reactivo 19: La hipérbola
¿Cuánto vale a en la hipérbola con la ecuación \frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{9}^{2}}=1 , si c=41 ?
Solución:
Los parámetros a , b y c en la hipérbola forman un triángulo rectángulo comprendido entre el eje menor y cualquiera de los senos de la cónica.
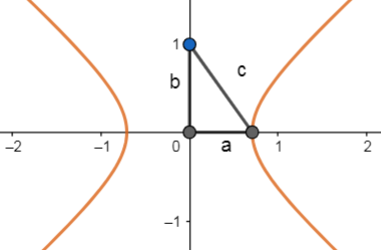
Por tanto, conociendo a dos de estos parámetros podemos calcular al restante aplicando el Teorema de Pitágoras.
{c}^{2}={b}^{2}+{a}^{2}
{a}^{2}={c}^{2}-{b}^{2}\to a=\sqrt{{c}^{2}-{b}^{2}}
Del enunciado sabemos que: c=41 y b=9 . Sustituimos y calculamos.
a=\sqrt{{\left(41\right)}^{2}-{\left(9\right)}^{2}}=40
El valor del parámetro a es de 40.
Nota: a representa la distancia entre el vértice de la hipérbola y el eje menor.
Concluimos indicando como respuesta correcta a la opción D.
Reactivo 20: Ecuación de la elipse
Elige la ecuación que represente a la cónica de la figura.
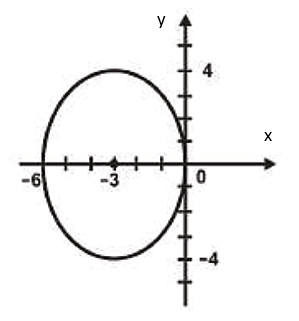
Solución:
El problema solicita que determinemos la ecuación canónica de la elipse, con centro en \left(-3, 0\right) y eje mayor paralelo a las y .
\frac{{\left(x-h\right)}^{2}}{{b}^{2}}+\frac{{\left(y-k\right)}^{2}}{{a}^{2}}=1
En este caso, la a se ha colocado debajo de las y porque dicho parámetro representa al eje de mayor tamaño. El valor de a y b se obtiene de la gráfica; a es la mitad del eje mayor y b la mitad del eje menor.
a=\frac{8}{2}=4
b=\frac{6}{2}=3
Ahora, sustituimos en la ecuación ordinaria.
\frac{{\left(x+3\right)}^{2}}{{3}^{2}}+\frac{{\left(y-0\right)}^{2}}{{4}^{2}}=1
\frac{{\left(x+3\right)}^{2}}{9}+\frac{{y}^{2}}{16}=1
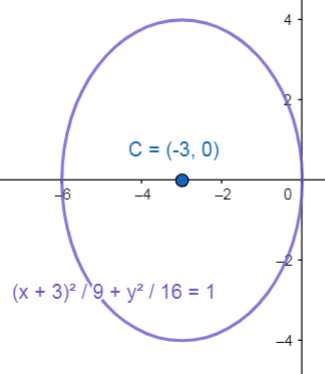
Comparando el resultado con los incisos, seleccionamos como respuesta correcta al D.
Reactivo 21: Límite de una función
Calcula el límite \underset{x\to 0}{lim} \frac{\sqrt{2+x}-\sqrt{2}}{x}
Solución:
Para resolver cualquier límite debemos, antes que nada, evaluar a la función en el punto dado. Si obtenemos como resultado un número o infinito, concluimos el ejercicio; si por el contrario es una indeterminación, debemos aplicar artificios matemáticos o alguna otra técnica de resolución.
Evaluando el límite.
\underset{x\to 0}{lim} \frac{\sqrt{2+x}-\sqrt{2}}{x}=\frac{\sqrt{2+0}-\sqrt{2}}{0}=\frac{0}{0}
Indeterminación cero entre cero, debemos romperla.
En este caso, es conveniente multiplicar y dividir por el conjugado del numerador; porque el denominador no puede simplificarse más.
\underset{x\to 0}{lim} \frac{\sqrt{2+x}-\sqrt{2}}{x}*\frac{\sqrt{2+x}+\sqrt{2}}{\sqrt{2+x}+\sqrt{2}}=\underset{x\to 0}{lim} \frac{{\left(\sqrt{2+x}\right)}^{2}-{\left(\sqrt{2}\right)}^{2}}{x\left(\sqrt{2+x}+\sqrt{2}\right)}
\underset{x\to 0}{lim} \frac{2+x-2}{x\left(\sqrt{2+x}+\sqrt{2}\right)}=\underset{x\to 0}{lim} \frac{x}{x\left(\sqrt{2+x}+\sqrt{2}\right)}=\underset{x\to 0}{lim} \frac{1}{\sqrt{2+x}+\sqrt{2}}
Llegados a este punto, procedemos a evaluar.
\underset{x\to 0}{lim} \frac{1}{\sqrt{2+x}+\sqrt{2}}=\frac{1}{\sqrt{2+0}+\sqrt{2}}=\frac{1}{2\sqrt{2}}
Racionalizamos el resultado.
\frac{1}{2\sqrt{2}}=\frac{\sqrt{2}}{2\left(2\right)}=\frac{\sqrt{2}}{4}
Concluimos seleccionando como respuesta correcta la opción D.
Reactivo 22: Derivada por definición
¿Cuál de las siguientes expresiones corresponde para obtener la derivada f\left(x\right)={x}^{3} en el punto x=3 ?
Solución:
Aunque no se indique explícitamente, el ejercicio está solicitando que obtengamos la derivada por definición de la función f\left(x\right)={x}^{3} . Para ello, empleamos el siguiente límite:
{f}^{\text{'}}\left(x\right)=\frac{f\left(x+h\right)-f\left(x\right)}{h}
Como la variable del límite es h podemos sustituir directamente el punto de x al que queremos evaluar la derivada, es decir x=3 .
{f}^{\text{'}}\left(3\right)=\frac{f\left(3+h\right)-f\left(3\right)}{h}
Ahora, sustituimos f\left(3+h\right)={\left(3+h\right)}^{3} y f\left(3\right)={3}^{3} .
{f}^{\text{'}}\left(3\right)=\frac{{\left(3+h\right)}^{3} -{3}^{3}}{h}
Desarrollamos.
{f}^{\text{'}}\left(3\right)=\frac{{\left(3+h\right)}^{3} -{3}^{3}}{h}= \frac{{3}^{3}+3\bullet {3}^{2}h+3{\bullet 3h}^{2}+{h}^{3} -{3}^{3}}{h}
Escrito todo el desarrollo en una misma línea quedaría:
{f}^{\text{'}}\left(3\right)=\frac{f\left(3+h\right)-f\left(3\right)}{h} =\frac{{\left(3+h\right)}^{3} -{3}^{3}}{h}
{f}^{\text{'}}\left(3\right)=\frac{{3}^{3}+3\bullet {3}^{2}h+3{\bullet 3h}^{2}+{h}^{3} -{3}^{3}}{h}
Comparando con las opciones, la respuesta correcta es la A.
Reactivo 23: Máximos y mínimos de una función
Indica las coordenadas de los puntos máximos y mínimos de la función y=x(x-4{)}^{2} , con 0\le x\le 4
Solución:
El procedimiento general para obtener los máximos y mínimos relativos en un intervalo cerrado \left[a, b\right] de una función es:
- Calcular la derivada de f
- Determinar las raíces de {f}^{\text{'}} , también llamados números críticos. Aquellos valores de x donde la derivada se hace cero
- Con los número críticos (dentro del intervalo) \left\{{c}_{1}, {c}_{2}, {c}_{3}, \dots \right\} , se procede a calcular la imagen para cada uno de ellos f\left({c}_{1}\right), f\left({c}_{2}\right), f\left({c}_{3}\right) , como también la imagen de la función en los extremos
- Se comparan, el mayor valor será el Máximo relativo del intervalo y el menor valor el Mínimo relativo del intervalo
Cálculo de la derivada.
y=x(x-4{)}^{2}\to {y}^{\text{'}}={x}^{\text{'}}(x-4{)}^{2}+x[{(x-4{)}^{2}]}^{\text{'}}
{y}^{\text{'}}=(x-4{)}^{2}+2x{\left(x-4\right)}^{2-1}{\left(x-4\right)}^{\text{'}}
{y}^{\text{'}}=(x-4{)}^{2}+2x\left(x-4\right)=\left(x-4\right)\left(x-4+2x\right)
\therefore {y}^{\text{'}}=\left(x-4\right)\left(3x-4\right)
Determinación de los números críticos.
Igualamos la derivada a cero y calculamos sus raíces.
{y}^{\text{'}}=0\to \left(x-4\right)\left(3x-4\right)=0
La derivada se hace cero cuando:
x-4=0\to x=4
3x-4=0\to x=\frac{4}{3}
Ambos números críticos pertenecen al intervalo \left[0, 4\right] y x=4 es además, el extremo superior del intervalo.
Imagen de números críticos y extremos del intervalo.
Para los extremos.
f\left(0\right)=\left(0\right)(0-4{)}^{2}=0
f\left(4\right)=\left(4\right)(4-4{)}^{2}=0
Para los números críticos.
f\left(\frac{4}{3}\right)=\left(\frac{4}{3}\right){\left(\frac{4}{3}-4\right)}^{2}=\frac{4}{3}*\frac{64}{9}=\frac{256}{27}

Conclusión:
Máximo \left(\frac{4}{3}, \frac{256}{27}\right)
Mínimo \left(4, 0\right)
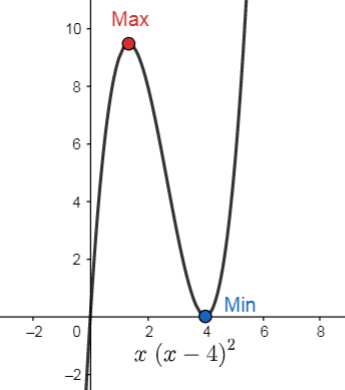
Comparando con las opciones, la respuesta correcta es la D.
Reactivo 24: Optimización
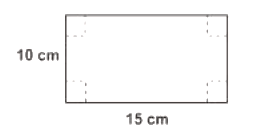
Se desea fabricar una caja sin tapa con una lámina de 10 cm x 15 cm. ¿Cuánto se deberá cortar en cada esquina de la lámina para obtener el volumen máximo?
Solución:
En este problema de optimización, debemos estimar cuánto hay que cortar en las esquinas para que al doblar las solapas resultantes, el volumen sea el máximo posible. Antes de pasar a modelar el volumen de la caja, haremos algunas consideraciones.
- Los recortes tienen forma cuadrada, es decir, la misma longitud en todos sus lados
- No se dejarán pestañas para pegar una solapa con otra
A cada lado del cuadrado de la esquina que recortaremos le llamaremos x y será nuestra variable.
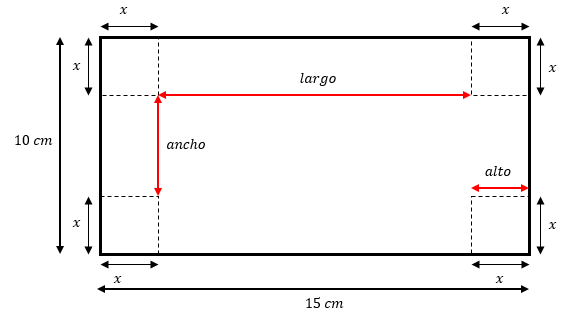
En la figura, podemos ver (en negro) las dimensiones de la lámina de cartón antes de ser doblada y (en rojo) las dimensiones que tendrá una vez haya sido recortada. De ella, podemos extraer las siguientes expresiones para el largo l , ancho a y alto h :
l=15-2x
a=10-2x
h=x
Volumen de una caja.
v=l*a*h
Sustituimos.
v=\left(15-2x\right)\left(10-2x\right)x
Desarrollamos.
v=4{x}^{3}-50{x}^{2}+150x
Ahora, debemos encontrar el máximo global del volumen respecto a la longitud de corte x . Solo nos queda derivar, encontrar los números críticos, evaluarlos en el volumen y determinar cuál es el mayor.
\frac{dv}{dx}={\left(4{x}^{3}-50{x}^{2}+150x\right)}^{\text{'}}=12{x}^{2}-100x+150
Igualamos a cero la derivada.
{v}^{\text{'}}=0\to 12{x}^{2}-100x+150=0
6{x}^{2}-50x+75=0
Aplicamos la resolución de segundo grado para hallar los números críticos.
x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}
a=6;b=-50;c=75
x=\frac{50\pm \sqrt{{50}^{2}-4\left(6\right)\left(75\right)}}{2\left(6\right)}=\frac{25\pm 5\sqrt{7}}{6}
{x}_{1}=\frac{25+5\sqrt{7}}{6}\cong 6.3714\dots
{x}_{2}=\frac{25-5\sqrt{7}}{6}\cong 1.9618\dots
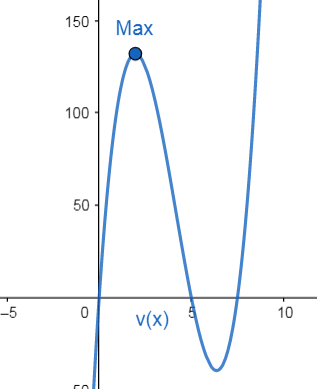
Incluso antes de evaluar, sabremos que {x}_{1} no es el máximo porque implica un corte mayor a 5 cm, el cual es el límite de corte que podríamos hacer en la lámina. De igual forma, evaluamos.
v\left({x}_{1}\right)=-39.44\dots
v\left({x}_{2}\right)=132.03\dots
La longitud {x}_{2} es el corte que debemos realizar para obtener el mayor volumen posible.
{x}_{MAX}=\frac{25-5\sqrt{7}}{6}
Seleccionamos como respuesta correcta a la opción D.
Reactivo 25: Integral definida
El valor de la integral definida {\int }_{0}^{2}{x}^{2}dx\mathrm{ } es igual a:
Solución:
Para integrar definidamente, debemos primero integrar de forma indefinida (aplicando fórmulas, propiedades y los métodos que hagan falta), para finalizar aplicando el Segundo Teorema Fundamental del Cálculo con los límites de integración.
{\int }_{a}^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right)
Donde F es la primitiva de f . Integramos la función cuadrática.
i={\int }_{0}^{2}{x}^{2}dx
Integral de una potencia:
{\int }_{0}^{2}{x}^{2}dx=\frac{{x}^{2+1}}{2+1}|2 0 =\frac{{x}^{3}}{3}|2 0
Evaluamos aplicando el STFC.
i=\frac{{x}^{3}}{3}|2 0 =\frac{{\left(2\right)}^{3}}{3}-\frac{{\left(0\right)}^{3}}{3}=\frac{8}{3}
Finalmente:
{\int }_{0}^{2}{x}^{2}dx=\frac{8}{3}
Comparando con las opciones, seleccionamos como correcta la C.
Reactivo 26: Integral Indefinida
La \int {\left(2x-1\right)}^{3}dx es igual a:
Solución:
Podemos seguir dos caminos para resolver esta integral: desarrollamos la potencia al cubo o aplicamos cambio de variable. La segunda alternativa es más práctica y rápida.
\int {\left(2x-1\right)}^{3}dx
Hacemos el cambio de variable a la base de la potencia.
v=2x-1\to dv=2dx
\therefore dx=\frac{1}{2}dv
Sustituimos.
\int {\left(2x-1\right)}^{3}dx\to \frac{1}{2}\int {v}^{3}dv
Integramos aplicando la fórmula de integral de una potencia.
\frac{1}{2}\int {v}^{3}dv=\frac{1}{2}\frac{{v}^{3+1}}{3+1}+c=\frac{{v}^{4}}{8}+c
Devolvemos el cambio de variable.
\frac{{v}^{4}}{8}+c\to \frac{{\left(2x-1\right)}^{4}}{8}+c
Finalmente.
\int {\left(2x-1\right)}^{3}dx=\frac{{\left(2x-1\right)}^{4}}{8}+c
Escogemos como correcta la opción D.

