En este simulacro de examen vamos a resolver 26 ejercicios del área 1 de matemáticas paso a paso con el objetivo de que practiques antes de presentar el examen de ingreso a la UNAM.

Estos ejercicios han sido creados en guías pasadas de la universidad, sin embargo, los temas del examen actual siguen siendo los mismos.

El área 1 corresponde a las ciencias físico matemáticas y de las ingenierías, la principal característica y diferencia con las otras áreas es que incluye los temas de límites, cálculo diferencial y integral en el área de matemáticas.

Antes de consultar la respuesta te recomiendo intentar resolverlos por cuenta propia.

Estructura del examen

El examen que vas a presentar tiene un total de 120 reactivos, mismos que deberás resolver en 3 horas.

Conoce todos los temas del examen de la UNAM con la guía oficial

En total son 9 materias, de las cuales las que tienen mayor peso en tu calificación son español, matemáticas y física.

Conoce la estructura del examen de la UNAM para el área 1

Temario matemáticas UNAM

Los siguientes temas de la lista corresponden al temario de matemáticas para el área 1 de la guía UNAM para el examen de admisión.

Recuerda que el Área 1 (ciencias físico matemáticas y de las ingenierías), incluye una parte adicional de cálculo diferencial e integral. Te recomiendo consultar la convocatoria UNAM para conocer todo sobre el proceso de admisión vigente.

Estos son los temas que tienes que estudiar:

Simulacro de Matemáticas Área 1

Durante el simulacro, además de explicarte los reactivos hemos indicado el tema al que pertenecen, de esta manera podrás profundizar en los temas que más se te dificulten, recuerda que los exámenes simulacro tienen dos objetivos:

1. Practicar e identificar los temas que se te dificultan más.
2. Desarrollar tu agilidad al momento de responderlos, recuerda que tienes un tiempo límite.

Dicho todo lo anterior vamos a comenzar con la solución de este examen.

Reactivo 1: Elementos de la división

Si 127 es el dividendo y 11 es el divisor en la ecuación, ¿Cuál es el valor del cociente c y el residuo r ?

1. c=13 ; r=-16
2. c=12 ; r=-5
3. c=10 ; r=17
4. c=11 ; r=6

Solución:

Para encontrar el valor del cociente y el residuo, debemos realizar la división de 127 entre 11.

Bajamos el 12 y buscamos un número para el cociente que multiplicado por 11 sea 12 o se le acerque, que en este caso el 1.

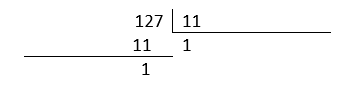
Bajamos el 7, quedando el residuo como 17. De nuevo, el número que multiplicado por 11 se acerca a 17 es 1.

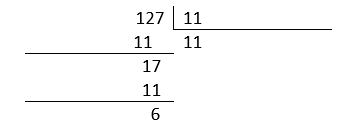
Llegados a este punto, el cociente es 11 y el residuo 6. La división 127÷11 puede ser expresada como:

127÷11=11*11+6

c=11 y r=6

Concluimos el problema escogiendo como respuesta correcta al inciso D.

Reactivo 2: Simplificación de potencias

Simplifica la expresión \frac{{\left({a}^{2}+b\right)}^{\frac{3}{2}}}{{a}^{2}+b}

1. \sqrt{{\left({a}^{2}+b\right)}^{6}}
2. {\left({a}^{2}+b\right)}^{-\frac{1}{2}}
3. \sqrt{{a}^{2}+b}
4. a+{b}^{\frac{1}{2}}

Solución:

El problema solicita que simplifiquemos la expresión fraccionaria, para ello, emplearemos la propiedad de división se potencias de igual base.

Observemos que, tanto en el numerador como en el denominador se encuentra el binomio {a}^{2}+b . En el numerador elevado a 3/2 y en el denominador a 1.

\frac{{\left({a}^{2}+b\right)}^{\frac{3}{2}}}{{a}^{2}+b}=\frac{{\left({a}^{2}+b\right)}^{\frac{3}{2}}}{{\left({a}^{2}+b\right)}^{1}}

La propiedad del cociente de potencias de igual base dice que: se conserva la misma base y se restan los exponentes.

\frac{{\left({a}^{2}+b\right)}^{\frac{3}{2}}}{{\left({a}^{2}+b\right)}^{1}}={\left({a}^{2}+b\right)}^{\frac{3}{2}-1}

Resolvemos la resta en el exponente.

{\left({a}^{2}+b\right)}^{\frac{3}{2}-1}={\left({a}^{2}+b\right)}^{\frac{1}{2}}

Cuando el exponente es \frac{1}{2} , la potencia puede transformarse a un radical de índice igual a 2 o raíz cuadrada.

{\left({a}^{2}+b\right)}^{\frac{1}{2}}=\sqrt{{a}^{2}+b}

Concluimos el problema seleccionando la C como respuesta correcta.

Reactivo 3: Productos notables

Al desarrollar {\left({x}^{2}-3y\right)}^{3}   se obtiene:

1. {x}^{6}-9{x}^{4}y+27{x}^{2}{y}^{2}+27{y}^{3}
2. {x}^{6}+9{x}^{4}y-27{x}^{2}{y}^{2}+27{y}^{3}
3. {x}^{6}-9{x}^{4}y+27{x}^{2}{y}^{2}-27{y}^{3}
4. {x}^{6}+9{x}^{4}y-27{x}^{2}{y}^{2}-27{y}^{3}

Solución:

Para desarrollar rápidamente la expresión del problema, recurriremos al producto notable del cubo de la diferencia de dos cantidades:

(a-b{)}^{3}={a}^{3}-3{a}^{2}b+3a{b}^{2}-{b}^{3}

En nuestro caso a es {x}^{2} y b es 3y . Procedemos al desarrollo.

{\left({x}^{2}-3y\right)}^{3}={\left({x}^{2}\right)}^{3}-3{\left({x}^{2}\right)}^{2}\left(3y\right)+3\left({x}^{2}\right){\left(3y\right)}^{2}-{\left(3y\right)}^{3}

Resolvemos las potencias y productos pendientes.

={x}^{6}-9{x}^{4}y+27{x}^{2}{y}^{2}-27{y}^{3}

Finalmente, el desarrollo de {\left({x}^{2}-3y\right)}^{3} es {x}^{6}-9{x}^{4}y+27{x}^{2}{y}^{2}-27{y}^{3} .

En base a las expresiones de cada inciso, seleccionamos como respuesta correcta al C.

Reactivo 4: Fracciones algebraicas

Simplifica la siguiente fracción.

\frac{-{x}^{2}-3x+40}{x+8}

1. x-5
2. -x+5
3. -x+8
4. x-8

Solución:

Para encontrar la forma simplificada de la expresión, debemos representar al trinomio del numerador como el producto de sus factores primos, es decir, factorizar el trinomio cuadrado.

Extraemos factor común el signo menos.

\frac{-{x}^{2}-3x+40}{x+8}=-\frac{{x}^{2}+3x-40}{x+8}

Existen diferentes vías para factorizar el trinomio, en este caso intentaremos encontrar dos números que multiplicados sean -40 y sumados 3, dichas cantidades son 8 y -5.

8*-5=40

8+\left(-5\right)=8-5=3

Reescribimos el trinomio.

-\frac{{x}^{2}+3x-40}{x+8}=-\frac{\left(x-5\right)\left(x+8\right)}{x+8}

Ahora, vemos que se simplifican los monomios x+8 presentes en el numerador y el denominador.

-\frac{\left(x-5\right)\left(x+8\right)}{x+8}=-\left(x-5\right)

Distribuimos el signo menos.

-\left(x-5\right)=-x+5

Indicamos finalmente que:

\frac{-{x}^{2}-3x+40}{x+8}=-x+5

Examinando las opciones que ofrece el problema, escogemos como correcta la B.

Reactivo 5: Ecuaciones e identidades

Selecciona la expresión que corresponde a una ecuación.

1. \mathrm{sin}\left(x\right)=\frac{1}{2}
2. \mathrm{sin}\left(x\right)=\frac{1}{2}x
3. {\mathrm{sin}}^{2}\left(x\right)+{\mathrm{cos}}^{2}\left(x\right) =1
4. {\mathrm{sec}}^{2}\left(x\right) -{\mathrm{tan}}^{2}\left(x\right) =1

Solución:

En este caso, debemos saber diferenciar entre ecuación e identidad. Ambas están conformadas por dos miembros y un signo de igualdad pero, la ecuación solo se cumple para ciertos valores de la variable y la identidad se cumple para todos sus posibles valores.

De entre los incisos, la única que cumple con esta condición es el inciso A, porque el seno de x valdrá \frac{1}{2} para ciertos valores de su argumento. Por otro lado C y D, son la identidad Pitagórica en términos de seno y coseno, y de tangente con secante, respectivamente.

El inciso B es una ecuación trascendental con dos posibles soluciones y podría, al igual que la opción A, ser la respuesta correcta. Teniendo en cuenta todo este análisis, seleccionamos como correcta a la opción A y a la B.

Consulta la oferta académica completa de la UNAM

Reactivo 6: Ecuaciones de segundo grado

Los valores que satisfacen la ecuación 6{x}^{2}-11x-35=0 , son:

1. {x}_{1}=\frac{5}{3};{x}_{2}=-\frac{7}{2}
2. {x}_{1}=-\frac{5}{3};{x}_{2}=-\frac{7}{2}
3. {x}_{1}=-\frac{5}{3};{x}_{2}=\frac{7}{2}
4. {x}_{1}=\frac{5}{3};{x}_{2}=\frac{7}{2}

Solución:

Para encontrar los valores que satisfacen a la ecuación, debemos aplicar la fórmula de segundo grado.

a{x}^{2}+bx+c=0

x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}

En este caso, los coeficientes a , b y c son:

a=6;b=-11;c=-35

Sustituimos y resolvemos.

{x}_{\mathrm{1,2}}=\frac{-\left(-11\right)\pm \sqrt{{\left(-11\right)}^{2}-4\left(6\right)\left(-35\right)}}{2\left(6\right)}=\frac{11\pm \sqrt{121+840}}{12}

{x}_{\mathrm{1,2}}=\frac{11\pm \sqrt{121+840}}{12}=\frac{11\pm \sqrt{961}}{12}=\frac{11\pm 31}{12}

Separamos las soluciones.

{x}_{1}=\frac{11-31}{12}=-\frac{5}{3}

{x}_{2}=\frac{11+31}{12}=\frac{7}{2}

Finalmente:

{x}_{1}=-\frac{5}{3};{x}_{2}=\frac{7}{2}

Comparando con las opciones, la respuesta correcta se encuentra en el inciso C.

Reactivo 7: Desigualdades y conjuntos

Selecciona la desigualdad que tiene por solución al conjunto (-\infty ,\frac{1}{3}]

1. 3x-1\ge 0
2. x-3\ge 0
3. -3x+1\ge 0
4. -x+3\ge 0

Solución:

Para facilitar el análisis, podemos graficar al conjunto indicado en el enunciado en una recta numérica:

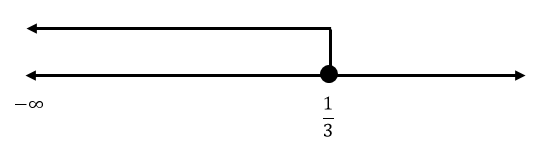
Son todos los números menores o iguales que \frac{1}{3} .

x\le \frac{1}{3}

Multiplicamos ambos lados de la desigualdad pos +3.

3x\le 1

Le restamos 1 a ambos lados.

3x-1\le 0

Si comparamos este resultado con los incisos, nos daremos cuenta que no se encuentra expresado de esta forma. Multipliquemos por -1 toda la inecuación.

-3x+1\ge 0

Ahora sí, seleccionamos como respuesta correcta el inciso C.

Reactivo 8: Sistema de ecuaciones lineales

Soluciona el sistema de ecuaciones

\left\{\begin{array}{c}5x+2y-z=-7 \\ x-2y+2z=0\\ 3y+z=17\end{array}\right.

1. x=-2,y=3,z=5
2. x=2,y=4,z=-5
3. x=-2,y=4,z=5
4. x=2,y=3,z=-5

Solución:

Para resolver el sistema de ecuaciones 3×3 del enunciado, podemos recurrir a los métodos: por sustitución, por igualación, por reducción o emplear la regla de Cramer.

En esa ocasión, emplearemos sustitución. Despejamos a z de la tercera ecuación, el resultado lo reemplazamos en 1 y 2 para obtener un sistema 2×2 más chico.

Despejando a z .

3y+z=17\to z=17-3y

Sustituyendo en 1.

5x+2y-\left(17-3y\right)=-7

5x+2y-17+3y=-7

5x+5y=17-7

5x+5y=10

Dividimos entre 5.

x+y=2

Sustituyendo z en 2.

x-2y+2\left(17-3y\right)=0

x-2y+34-6y=0

x-8y=-34

Nuevo sistema:

\left\{\begin{array}{c}x+y=2\\ x-8y=-34\end{array}\right.

Despejamos a x de x+y=2 .

x+y=2\to x=2-y

Sustituimos en x-8y=-34 .

2-y-8y=-34

-9y=-36

\therefore y=4

Sustituimos este resultado en x=2-y .

x=2-4=-2

\therefore x=-2

Por último, para obtener a z sustituimos el valor de y en z=17-3y .

z=17-3\left(4\right)=5

\therefore z=5

La solución al SEL es:

x=-2;y=4;z=5

Comparando con los incisos, la respuesta correcta es la C.

¿Sabes cuantos puntos necesitas para ser aceptado? Aciertos por carrera lista completa

Reactivo 9: Evaluar funciones

¿Cuál es el valor de y en x=-8 si y=5{x}^{\frac{2}{3}}+3x ?

1. -44
2. 8
3. 16
4. -4

Solución:

Para encontrar el valor de y cuando x=-8 , debemos sustituir todas las x por un -8 entre paréntesis y luego resolver las operaciones correspondientes respetando su jerarquía.

Sustituimos.

x=-8\to y=5{\left(-8\right)}^{\frac{2}{3}}+3\left(-8\right)

El {\left(-8\right)}^{\frac{2}{3}} puede escribirse como \sqrt[3]{{\left(-8\right)}^{2}} por propiedades de los exponentes.

y=5\sqrt[3]{{\left(-8\right)}^{2}}+3\left(-8\right)

Calculamos el cuadrado de -8.

y=5\sqrt[3]{64}+3\left(-8\right)

Ahora su raíz cúbica.

y=5\left(4\right)+3\left(-8\right)

Por último, resolvemos multiplicaciones.

y=20-24

y=-4

Comparando con las opciones, la respuesta correcta es el inciso D.

Reactivo 10: Trigonometría

¿Cuál es el seno del ángulo A en el siguiente triángulo rectángulo?

1. \frac{3}{5}
2. \frac{4}{5}
3. \frac{5}{3}
4. \frac{5}{4}

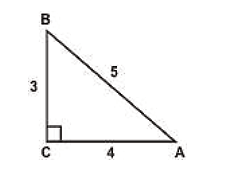
Solución:

De las identidades trigonométricas, sabemos que el seno de uno de los ángulos en un triángulo rectángulo es igual al cociente entre el cateto opuesto y la hipotenusa.

sin\alpha  =\frac{CO}{H}

En este caso, el ángulo en cuestión es A , su cateto opuesto es el que mide 3 unidades y la hipotenusa el lado más largo de 5 unidades. Sustituimos y concluimos indicando que:

sinA =\frac{3}{5}

El seno de A es igual a 3 sobre cinco.

Seleccionamos como correcta la opción A.

Reactivo 11: Trigonometría

En un triángulo rectángulo, la hipotenusa mide 10 unidades y uno de sus ángulos es de 30°. ¿Cuántas unidades mide el lado opuesto al ángulo dado?

1. 6
2. \frac{1}{20}
3. 5
4. \frac{15}{\sqrt{3}}

Solución:

Para visualizar con mayor facilidad lo que solicita el problema, haremos un pequeño bosquejo del triángulo rectángulo.

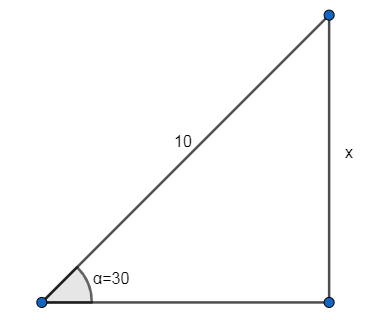
La hipotenusa vale 10 unidades, el ángulo de 30 grados entre la hipotenusa y uno de los catetos y x que representa al cateto cuya magnitud es desconocida. Para calcularlo, solo debemos recurrir al seno de 30 grados.

sin30 =\frac{CO}{H}=\frac{x}{10}

Despejamos.

x=10sin 30 =10*\frac{1}{2}=5

El cateto opuesto al ángulo de 30 grados mide 5 unidades.

Comparando con las opciones del problema, la respuesta correcta es la C.

Reactivo 12: Rango de una función real

Calcula el rango de la siguiente función y={e}^{\left(-5x-\frac{1}{5}\right)}+5 .

1. [\frac{1}{5},\infty )
2. \left(5,\infty \right)
3. \left(-5,\infty \right)
4. [-\frac{1}{5},\infty )

Solución:

Para calcular el rango de una función, primero debemos obtener la inversa de f , es decir cambiar de lugar a x y y . Luego, determinamos el dominio de {f}^{-1} ; dicho conjunto solución será el rango de f .

Cálculo de la inversa de f\left(x\right) , debemos despejar a la variable x .

y={e}^{\left(-5x-\frac{1}{5}\right)}+5

{e}^{\left(-5x-\frac{1}{5}\right)}=y-5

Logaritmo natural a ambos lados.

ln {e}^{\left(-5x-\frac{1}{5}\right)} =ln \left(y-5\right) 

-5x-\frac{1}{5}=ln \left(y-5\right) 

-5x=ln \left(y-5\right) +\frac{1}{5}

\therefore x=-\frac{1}{5}ln\left(y-5\right) -\frac{1}{25}

Ahora, calculamos el dominio de esta función inversa. Al término independiente lo podemos obviar porque vale igual para todos los reales, solo queda el término con el logaritmo natural, cuyo argumento debe ser mayor que cero.

-\frac{1}{5}ln\left(y-5\right) \exists \leftrightarrow y-5>0

Resolvemos la inecuación.

y-5>0\to y>5

Expresado en notación de intervalo.

\left(5,+\infty \right)

Concluimos que:

Ran\left\{{e}^{\left(-5x-\frac{1}{5}\right)}+5\right\}=\forall  y\in \left(5,\infty \right)

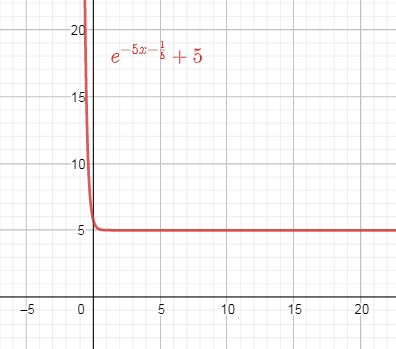
Gráfica de y={e}^{\left(-5x-\frac{1}{5}\right)}+5 . En ella, se evidencia que la función tiene un rango definido entre 5 y +\infty  .

Comparando con las opciones, escogemos como respuesta correcta al inciso B.

Reactivo 13: Punto medio

Encuentra las coordenadas del punto medio entre los puntos P\left(\mathrm{0,2}\right) y Q\left(\mathrm{4,6}\right) .

1. \left(\mathrm{2,3}\right)
2. \left(\mathrm{2,4}\right)
3. \left(\mathrm{3,3}\right)
4. \left(\mathrm{3,4}\right)

Solución:

El punto medio M de un segmento con extremos P y Q , es aquel que lo divide en dos partes iguales. Las coordenadas de dicho punto se calculan mediante la siguiente expresión:

M\left(\frac{{P}_{x}+{Q}_{x}}{2},\frac{{P}_{y}+{Q}_{y}}{2}\right)

Sustituimos las coordenadas de P y Q .

M\left(\frac{0+4}{2},\frac{2+6}{2}\right)=M\left(\frac{4}{2},\frac{8}{2}\right)=M\left(\mathrm{2,4}\right)

Las coordenadas del punto medio entre P\left(\mathrm{0,2}\right) y Q\left(\mathrm{4,6}\right) son \left(\mathrm{2,4}\right) .

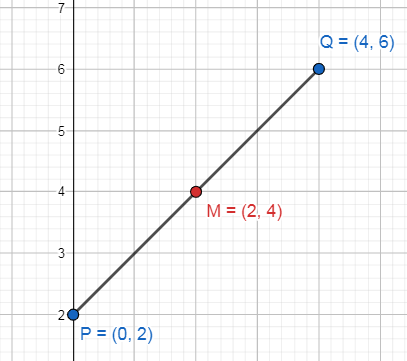
Concluimos el problema seleccionando como correcta a la opción B.

Reactivo 14: Distancia entre un punto y una recta

La distancia del punto \left(-\mathrm{1,1}\right) a la recta dada por la ecuación -3x+4y-8=0 es:

1. 1. X0.2 unidades
   2. X0.7 unidades

1. X1.2 unidades
2. X1.4 unidades

Solución:

En geometría Euclidiana, cuando hablamos de distancia entre elementos nos referimos a la distancia más corta entre ellos. Para la situación planteada en el problema, la distancia más corta es la que se haya trazando un segmento perpendicular desde la recta hasta el punto.

La magnitud de la distancia puede calcularse mediante la siguiente ecuación:

d=\left|\frac{A{x}_{p}+B{y}_{p}+C}{\sqrt{{A}^{2}+{B}^{2}}}\right|

Donde A , B y C son los coeficientes de la recta y {x}_{p}, {y}_{p} las coordenadas del punto. Sustituimos.

d=\left|\frac{-3\left(-1\right)+4\left(1\right)-8}{\sqrt{{\left(-3\right)}^{2}+{\left(4\right)}^{2}}}\right|=\left|\frac{3+4-8}{\sqrt{9+16}}\right|=\left|\frac{-1}{\sqrt{25}}\right|=\left|\frac{-1}{5}\right|

Eliminamos las barras de valor absoluto escribiendo a la cantidad interior positiva.

d=\left|\frac{-1}{5}\right|=\frac{1}{5}=0.2

La distancia entre el punto y la recta es de 0.2 unidades.

Comparando con las opciones, seleccionamos como correcta la A.

Reactivo 15: Problemas de distancia

En un marco de referencia representado por un plano XY , se localiza un gasoducto sobre la recta 3x+4y=2 con una fábrica en el punto \left(6, 6\right) . ¿Qué longitud, en metros, se requiere para conectar perpendicularmente a la fábrica con el gasoducto?

1. X7.8 m
2. X8.4 m
3. X8.0 m
4. X7.4 m

Solución:

Hagamos un rápido bosquejo de la situación planteada por el enunciado del problema.

Ya que nos piden la distancia perpendicular entre el punto y la recta, el problema se resume en la fórmula de distancia entre una recta y un punto.

d=\left|\frac{A{x}_{p}+B{y}_{p}+C}{\sqrt{{A}^{2}+{B}^{2}}}\right|

La ecuación de la recta debe estar en su forma ordinaria, pasamos al primer miembro el 2.

l:3x+4y-2=0

P\left(6, 6\right)

Sustituimos.

d=\left|\frac{3\left(6\right)+4\left(6\right)-2}{\sqrt{{\left(3\right)}^{2}+{\left(4\right)}^{2}}}\right|=\left|\frac{40}{\sqrt{25}}\right|=\left|\frac{40}{5}\right|=8

El ducto de conexión debe medir 8 metros.

Concluimos seleccionando como correcta a la opción C.

Reactivo 16: Centro de la circunferencia

Indica las coordenadas del centro de la circunferencia cuya ecuación general es 3{x}^{2}+3{y}^{2}+12x-30y+6=0

1. C\left(-\mathrm{4,10}\right)
2. C\left(-\mathrm{2,5}\right)
3. C\left(4,-10\right)
4. C\left(2,-5\right)

Solución:

Para encontrar las coordenadas del centro de la circunferencia, debemos aplicar completación de cuadrados a la ecuación en forma general, comencemos por la variable x .

Dividimos entre 3 toda la ecuación.

{x}^{2}+{y}^{2}+4x-10y+2=0

Agrupamos los términos con x .

{x}^{2}+4x+{y}^{2}-10y+2=0

Para completar cuadrados en x , sumamos y restamos 4.

{x}^{2}+4x+4+{y}^{2}-10y+2-4=0

{x}^{2}+4x+4+{y}^{2}-10y-2=0

Los términos {x}^{2}+4x+4 pueden escribirse como {\left(x+2\right)}^{2} .

{\left(x+2\right)}^{2}+{y}^{2}-10y-2=0

Para completar cuadrados en y , sumamos y restamos 25.

{\left(x+2\right)}^{2}+{y}^{2}-10y+25-2-25=0

{\left(x+2\right)}^{2}+{y}^{2}-10y+25-27=0

Los términos {y}^{2}-10y+25 pueden reescribirse como {\left(y-5\right)}^{2} .

{\left(x+2\right)}^{2}+{\left(y-5\right)}^{2}-27=0

{\left(x+2\right)}^{2}+{\left(y-5\right)}^{2}=27

Con la circunferencia en su forma ordinaria, extraemos por simple inspección las coordenadas del centro.

C\left(-\mathrm{2,5}\right)

Finalmente, indicamos la opción B como respuesta correcta.

Reactivo 17: Ecuación de la parábola

Selecciona la ecuación de la parábola con foco F\left(\mathrm{1,0}\right) , valor del parámetro P=1 y eje focal paralelo al eje x .

1. {x}^{2}+4y=0
2. {x}^{2}-4y=0
3. {y}^{2}-4x=0
4. {y}^{2}+4x=0

Solución:

La ecuación de una parábola con vértice en un punto \left(h,k\right) y con eje focal paralelo a las x es:

{\left(y-k\right)}^{2}=4p\left(x-h\right)

Tenemos el valor de P=1 que además, nos dice que la parábola abre hacia la derecha. Por otro lado, no conocemos las coordenadas del vértice, pero sí las del foco.

Como la parábola tiene el eje focal paralelo a las x , el vértice y el foco tienen la misma coordenada en y . Además, el vértice debe encontrarse detrás del foco, exactamente a -P unidades. En base a esto, las coordenadas del vértice son:

V=\left(1-P,0\right)=\left(1-\mathrm{1,0}\right)=\left(\mathrm{0,0}\right)

La parábola tiene vértice en el origen. Sustituimos.

{\left(y-0\right)}^{2}=4\left(1\right)\left(x-0\right)\to {y}^{2}=4x

\therefore {y}^{2}-4x=0

Concluimos seleccionando como respuesta correcta al inciso C.

Reactivo 18: Lugares geométricos y cónicas

Lugar geométrico en el plano de un punto cualquiera, que la suma de las distancias a dos puntos fijos llamados focos, es una cantidad constante.

1. Elipse
2. Circunferencia
3. Hipérbola
4. Parábola

Solución:

Recordemos la definición de elipse:

La elipse, es el lugar geométrico descrito por un punto P\left(x,y\right) donde la suma de las distancias respecto a otros dos puntos fijos llamados focos, es constante.

Si comparamos con lo enunciado en el problema, ambas definiciones describen al mismo lugar geométrico, por tanto, la respuesta correcta es la A Elipse.

Reactivo 19: La hipérbola

¿Cuánto vale a en la hipérbola con la ecuación \frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{9}^{2}}=1 , si c=41 ?

1. a=42
2. a=36
3. a=38
4. a=40

Solución:

Los parámetros a , b y c en la hipérbola forman un triángulo rectángulo comprendido entre el eje menor y cualquiera de los senos de la cónica.

Por tanto, conociendo a dos de estos parámetros podemos calcular al restante aplicando el Teorema de Pitágoras.

{c}^{2}={b}^{2}+{a}^{2}

{a}^{2}={c}^{2}-{b}^{2}\to a=\sqrt{{c}^{2}-{b}^{2}}

Del enunciado sabemos que: c=41 y b=9 . Sustituimos y calculamos.

a=\sqrt{{\left(41\right)}^{2}-{\left(9\right)}^{2}}=40

El valor del parámetro a es de 40.

Nota: a representa la distancia entre el vértice de la hipérbola y el eje menor.

Concluimos indicando como respuesta correcta a la opción D.

Sigue practicando con estos 50 ejercicios de matemáticas del examen para la UNAM

Reactivo 20: Ecuación de la elipse

Elige la ecuación que represente a la cónica de la figura.

1. \frac{(x-3{)}^{2}}{16}+\frac{{y}^{2}}{9}=1
2. \frac{(x-3{)}^{2}}{9}+\frac{{y}^{2}}{16}=1
3. \frac{(x+3{)}^{2}}{16}+\frac{{y}^{2}}{9}=1
4. \frac{(x+3{)}^{2}}{9}+\frac{{y}^{2}}{16}=1

Solución:

El problema solicita que determinemos la ecuación canónica de la elipse, con centro en \left(-3, 0\right) y eje mayor paralelo a las y .

\frac{{\left(x-h\right)}^{2}}{{b}^{2}}+\frac{{\left(y-k\right)}^{2}}{{a}^{2}}=1

En este caso, la a se ha colocado debajo de las y porque dicho parámetro representa al eje de mayor tamaño. El valor de a y b se obtiene de la gráfica; a es la mitad del eje mayor y b la mitad del eje menor.

a=\frac{8}{2}=4

b=\frac{6}{2}=3

Ahora, sustituimos en la ecuación ordinaria.

\frac{{\left(x+3\right)}^{2}}{{3}^{2}}+\frac{{\left(y-0\right)}^{2}}{{4}^{2}}=1

\frac{{\left(x+3\right)}^{2}}{9}+\frac{{y}^{2}}{16}=1

Comparando el resultado con los incisos, seleccionamos como respuesta correcta al D.

Reactivo 21: Límite de una función

Calcula el límite \underset{x\to 0}{lim} \frac{\sqrt{2+x}-\sqrt{2}}{x}

1. \frac{\sqrt{2}}{2}
2. \frac{2}{\sqrt{2}}
3. \frac{4}{\sqrt{2}}
4. \frac{\sqrt{2}}{4}

Solución:

Para resolver cualquier límite debemos, antes que nada, evaluar a la función en el punto dado. Si obtenemos como resultado un número o infinito, concluimos el ejercicio; si por el contrario es una indeterminación, debemos aplicar artificios matemáticos o alguna otra técnica de resolución.

Evaluando el límite.

\underset{x\to 0}{lim} \frac{\sqrt{2+x}-\sqrt{2}}{x}=\frac{\sqrt{2+0}-\sqrt{2}}{0}=\frac{0}{0}

Indeterminación cero entre cero, debemos romperla.

En este caso, es conveniente multiplicar y dividir por el conjugado del numerador; porque el denominador no puede simplificarse más.

\underset{x\to 0}{lim} \frac{\sqrt{2+x}-\sqrt{2}}{x}*\frac{\sqrt{2+x}+\sqrt{2}}{\sqrt{2+x}+\sqrt{2}}=\underset{x\to 0}{lim} \frac{{\left(\sqrt{2+x}\right)}^{2}-{\left(\sqrt{2}\right)}^{2}}{x\left(\sqrt{2+x}+\sqrt{2}\right)}

\underset{x\to 0}{lim} \frac{2+x-2}{x\left(\sqrt{2+x}+\sqrt{2}\right)}=\underset{x\to 0}{lim} \frac{x}{x\left(\sqrt{2+x}+\sqrt{2}\right)}=\underset{x\to 0}{lim} \frac{1}{\sqrt{2+x}+\sqrt{2}}

Llegados a este punto, procedemos a evaluar.

\underset{x\to 0}{lim} \frac{1}{\sqrt{2+x}+\sqrt{2}}=\frac{1}{\sqrt{2+0}+\sqrt{2}}=\frac{1}{2\sqrt{2}}

Racionalizamos el resultado.

\frac{1}{2\sqrt{2}}=\frac{\sqrt{2}}{2\left(2\right)}=\frac{\sqrt{2}}{4}

Concluimos seleccionando como respuesta correcta la opción D.

Reactivo 22: Derivada por definición

¿Cuál de las siguientes expresiones corresponde para obtener la derivada f\left(x\right)={x}^{3} en el punto x=3 ?

1. {f}^{\text{'}}\left(3\right)=\underset{h\to 0}{lim} \frac{f\left(3+h\right)-f\left(3\right)}{h}=\underset{h\to 0}{lim} \frac{(3+h{)}^{3}-{3}^{3}}{h} {f}^{\text{'}}\left(3\right)=\underset{h\to 0}{lim} \frac{{3}^{3}+3\cdot {3}^{2}h+3\cdot 3{h}^{2}+{h}^{3}-{3}^{3}}{h} 
2. {f}^{\text{'}}\left(3\right)=\underset{h\to 0}{lim} \frac{f\left(3\right)-f\left(3+h\right)}{h}=\underset{h\to 0}{lim} \frac{{3}^{3}-(3+h{)}^{3}}{h} {f}^{\text{'}}\left(3\right)=\underset{h\to 0}{lim} \frac{{3}^{3}-{3}^{3}-3\cdot {3}^{2}h-3\cdot 3{h}^{2}-{h}^{3}}{h} 
3. {f}^{\text{'}}\left(3\right)=\underset{h\to 0}{lim} \frac{f\left(3+h\right)+f\left(3\right)}{h}=\underset{h\to 0}{lim} \frac{(3+h{)}^{3}+{3}^{3}}{h} {f}^{\text{'}}\left(3\right)=\underset{h\to 0}{lim} \frac{{3}^{3}+3\cdot {3}^{2}h+3\cdot 3{h}^{2}+{h}^{3}+{3}^{3}}{h} 
4. {f}^{\text{'}}\left(3\right)=\underset{h\to 0}{lim} \frac{f\left(3\right)-f\left(3-h\right)}{h}=\underset{h\to 0}{lim} \frac{{3}^{3}-(3-h{)}^{3}}{h} {f}^{\text{'}}\left(3\right)=\underset{h\to 0}{lim} \frac{{3}^{3}-{3}^{3}+3\cdot {3}^{2}h-3\cdot 3{h}^{2}+{h}^{3}}{h} 

Solución:

Aunque no se indique explícitamente, el ejercicio está solicitando que obtengamos la derivada por definición de la función f\left(x\right)={x}^{3} . Para ello, empleamos el siguiente límite:

{f}^{\text{'}}\left(x\right)=\frac{f\left(x+h\right)-f\left(x\right)}{h} 

Como la variable del límite es h podemos sustituir directamente el punto de x al que queremos evaluar la derivada, es decir x=3 .

{f}^{\text{'}}\left(3\right)=\frac{f\left(3+h\right)-f\left(3\right)}{h} 

Ahora, sustituimos f\left(3+h\right)={\left(3+h\right)}^{3} y f\left(3\right)={3}^{3} .

{f}^{\text{'}}\left(3\right)=\frac{{\left(3+h\right)}^{3} -{3}^{3}}{h} 

Desarrollamos.

{f}^{\text{'}}\left(3\right)=\frac{{\left(3+h\right)}^{3} -{3}^{3}}{h}= \frac{{3}^{3}+3\bullet {3}^{2}h+3{\bullet 3h}^{2}+{h}^{3} -{3}^{3}}{h} 

Escrito todo el desarrollo en una misma línea quedaría:

{f}^{\text{'}}\left(3\right)=\frac{f\left(3+h\right)-f\left(3\right)}{h} =\frac{{\left(3+h\right)}^{3} -{3}^{3}}{h} 

{f}^{\text{'}}\left(3\right)=\frac{{3}^{3}+3\bullet {3}^{2}h+3{\bullet 3h}^{2}+{h}^{3} -{3}^{3}}{h} 

Comparando con las opciones, la respuesta correcta es la A.

Reactivo 23: Máximos y mínimos de una función

Indica las coordenadas de los puntos máximos y mínimos de la función y=x(x-4{)}^{2} , con 0\le x\le 4

1. \left(\frac{10}{7},\frac{36}{14}\right),\left(\mathrm{4,0}\right)
2. \left(\frac{5}{7},\frac{10}{13}\right),\left(\mathrm{4,4}\right)
3. \left(\frac{8}{3},\frac{128}{27}\right),\left(\mathrm{4,4}\right)
4. \left(\frac{4}{3},\frac{256}{27}\right),\left(\mathrm{4,0}\right)

Solución:

El procedimiento general para obtener los máximos y mínimos relativos en un intervalo cerrado \left[a, b\right] de una función es:

1. Calcular la derivada de f
2. Determinar las raíces de {f}^{\text{'}} , también llamados números críticos. Aquellos valores de x donde la derivada se hace cero
3. Con los número críticos (dentro del intervalo) \left\{{c}_{1}, {c}_{2}, {c}_{3}, \dots \right\} , se procede a calcular la imagen para cada uno de ellos f\left({c}_{1}\right), f\left({c}_{2}\right), f\left({c}_{3}\right) , como también la imagen de la función en los extremos
4. Se comparan, el mayor valor será el Máximo relativo del intervalo y el menor valor el Mínimo relativo del intervalo

Cálculo de la derivada.

y=x(x-4{)}^{2}\to {y}^{\text{'}}={x}^{\text{'}}(x-4{)}^{2}+x[{(x-4{)}^{2}]}^{\text{'}}

{y}^{\text{'}}=(x-4{)}^{2}+2x{\left(x-4\right)}^{2-1}{\left(x-4\right)}^{\text{'}}

{y}^{\text{'}}=(x-4{)}^{2}+2x\left(x-4\right)=\left(x-4\right)\left(x-4+2x\right)

\therefore {y}^{\text{'}}=\left(x-4\right)\left(3x-4\right)

Determinación de los números críticos.

Igualamos la derivada a cero y calculamos sus raíces.

{y}^{\text{'}}=0\to \left(x-4\right)\left(3x-4\right)=0

La derivada se hace cero cuando:

x-4=0\to x=4

3x-4=0\to x=\frac{4}{3}

Ambos números críticos pertenecen al intervalo \left[0, 4\right] y x=4 es además, el extremo superior del intervalo.

Imagen de números críticos y extremos del intervalo.

Para los extremos.

f\left(0\right)=\left(0\right)(0-4{)}^{2}=0

f\left(4\right)=\left(4\right)(4-4{)}^{2}=0

Para los números críticos.

f\left(\frac{4}{3}\right)=\left(\frac{4}{3}\right){\left(\frac{4}{3}-4\right)}^{2}=\frac{4}{3}*\frac{64}{9}=\frac{256}{27}

Ordenemos todo en la siguiente tabla.

Conclusión:

Máximo \left(\frac{4}{3}, \frac{256}{27}\right)

Mínimo \left(4, 0\right)

Comparando con las opciones, la respuesta correcta es la D.

Reactivo 24: Optimización

Se desea fabricar una caja sin tapa con una lámina de 10 cm x 15 cm. ¿Cuánto se deberá cortar en cada esquina de la lámina para obtener el volumen máximo?

1. \frac{25+5\sqrt{7}}{6}
2. \frac{25+5\sqrt{43}}{6}
3. \frac{25-5\sqrt{43}}{6}
4. \frac{25-5\sqrt{7}}{6}

Solución:

En este problema de optimización, debemos estimar cuánto hay que cortar en las esquinas para que al doblar las solapas resultantes, el volumen sea el máximo posible. Antes de pasar a modelar el volumen de la caja, haremos algunas consideraciones.

1. Los recortes tienen forma cuadrada, es decir, la misma longitud en todos sus lados
2. No se dejarán pestañas para pegar una solapa con otra

A cada lado del cuadrado de la esquina que recortaremos le llamaremos x y será nuestra variable.

En la figura, podemos ver (en negro) las dimensiones de la lámina de cartón antes de ser doblada y (en rojo) las dimensiones que tendrá una vez haya sido recortada. De ella, podemos extraer las siguientes expresiones para el largo l , ancho a y alto h :

l=15-2x

a=10-2x

h=x

Volumen de una caja.

v=l*a*h

Sustituimos.

v=\left(15-2x\right)\left(10-2x\right)x

Desarrollamos.

v=4{x}^{3}-50{x}^{2}+150x

Ahora, debemos encontrar el máximo global del volumen respecto a la longitud de corte x . Solo nos queda derivar, encontrar los números críticos, evaluarlos en el volumen y determinar cuál es el mayor.

\frac{dv}{dx}={\left(4{x}^{3}-50{x}^{2}+150x\right)}^{\text{'}}=12{x}^{2}-100x+150

Igualamos a cero la derivada.

{v}^{\text{'}}=0\to 12{x}^{2}-100x+150=0

6{x}^{2}-50x+75=0

Aplicamos la resolución de segundo grado para hallar los números críticos.

x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}

a=6;b=-50;c=75

x=\frac{50\pm \sqrt{{50}^{2}-4\left(6\right)\left(75\right)}}{2\left(6\right)}=\frac{25\pm 5\sqrt{7}}{6}

{x}_{1}=\frac{25+5\sqrt{7}}{6}\cong 6.3714\dots 

{x}_{2}=\frac{25-5\sqrt{7}}{6}\cong 1.9618\dots 

Incluso antes de evaluar, sabremos que {x}_{1} no es el máximo porque implica un corte mayor a 5 cm, el cual es el límite de corte que podríamos hacer en la lámina. De igual forma, evaluamos.

v\left({x}_{1}\right)=-39.44\dots 

v\left({x}_{2}\right)=132.03\dots 

La longitud {x}_{2} es el corte que debemos realizar para obtener el mayor volumen posible.

{x}_{MAX}=\frac{25-5\sqrt{7}}{6}

Seleccionamos como respuesta correcta a la opción D.

Reactivo 25: Integral definida

El valor de la integral definida {\int }_{0}^{2}{x}^{2}dx\mathrm{ }  es igual a:

1. -\frac{8}{3}
2. 2
3. \frac{8}{3}
4. 8

Solución:

Para integrar definidamente, debemos primero integrar de forma indefinida (aplicando fórmulas, propiedades y los métodos que hagan falta), para finalizar aplicando el Segundo teorema Fundamental del Cálculo con los límites de integración.

{\int }_{a}^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right)

Donde F es la primitiva de f . Integramos la función cuadrática.

i={\int }_{0}^{2}{x}^{2}dx

Integral de una potencia:

{\int }_{0}^{2}{x}^{2}dx=\frac{{x}^{2+1}}{2+1}|2 0 =\frac{{x}^{3}}{3}|2 0 

Evaluamos aplicando el STFC.

i=\frac{{x}^{3}}{3}|2 0 =\frac{{\left(2\right)}^{3}}{3}-\frac{{\left(0\right)}^{3}}{3}=\frac{8}{3}

Finalmente:

{\int }_{0}^{2}{x}^{2}dx=\frac{8}{3}

Comparando con las opciones, seleccionamos como correcta la C.

Reactivo 26: Integral Indefinida

La \int {\left(2x-1\right)}^{3}dx es igual a:

1. \frac{(2x-1{)}^{2}}{6}+c
2. \frac{(2x-1{)}^{4}}{4}+c
3. \frac{(2x-1{)}^{2}}{2}+c
4. \frac{(2x-1{)}^{4}}{8}+c

Solución:

Podemos seguir dos caminos para resolver esta integral: desarrollamos la potencia al cubo o aplicamos cambio de variable. La segunda alternativa es más práctica y rápida.

\int {\left(2x-1\right)}^{3}dx

Hacemos el cambio de variable a la base de la potencia.

v=2x-1\to dv=2dx

\therefore dx=\frac{1}{2}dv

Sustituimos.

\int {\left(2x-1\right)}^{3}dx\to \frac{1}{2}\int {v}^{3}dv

Integramos aplicando la fórmula de integral de una potencia.

\frac{1}{2}\int {v}^{3}dv=\frac{1}{2}\frac{{v}^{3+1}}{3+1}+c=\frac{{v}^{4}}{8}+c

Devolvemos el cambio de variable.

\frac{{v}^{4}}{8}+c\to \frac{{\left(2x-1\right)}^{4}}{8}+c

Finalmente.

\int {\left(2x-1\right)}^{3}dx=\frac{{\left(2x-1\right)}^{4}}{8}+c

Escogemos como correcta la opción D.