Continúa resolviendo la quinta y última parte del simulador de matemáticas para el área de Ciencias Sociales y Administrativas del Politécnico Nacional.

Si has llegado hasta aquí te felicito y te pregunto, ¿qué sigue?... Si quieres más materiales de estudio para tu preparación, ve al menú en donde encontraras cientos de ejercicios para que pongas a prueba tus conocimientos.
Reactivo 41
Dados dos conjuntos A y U , de tal forma que A es un subconjunto de B , ¿cuál sería el resultado de la operación A\cup U ?
- \left\{\varnothing \right\}
- U-A
- U-B
- U
Solución:
Cuando decimos que un conjunto A es subconjunto de otro B , significa que los elementos de A son una parte de los elementos de B .
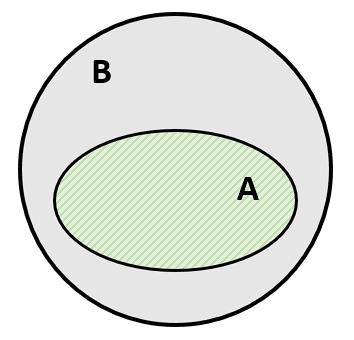
A\subset B
Una consecuencia de esto, es que la unión entre los conjuntos es B . Llevando esto a los conjuntos del problema, el resultado de la operación A\cup U=U debido a que A\subset U . La respuesta correcta es el inciso d).
Reactivo 42
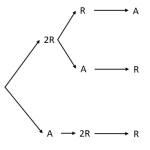
Determine el diagrama de árbol de un experimento aleatorio que consiste en extraer todas las bolas de una caja que contiene 2 bolas rojas y una azul.
Solución:
Para obtener el diagrama de árbol de todo el experimento, debemos reproducirlo teniendo en cuenta que las bolas no se reponen. En la primera extracción, podemos seleccionar una de las dos bolas rojas o la bola azul. Esto quedaría representado como:
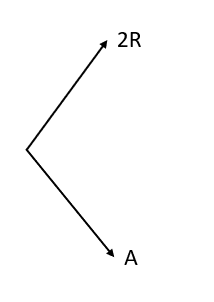
En el caso de seleccionar una roja, para la segunda extracción nos queda una roja y una azul. Si seleccionamos la azul en la primera, la siguiente tiene disponible solo las 2 bolas rojas.
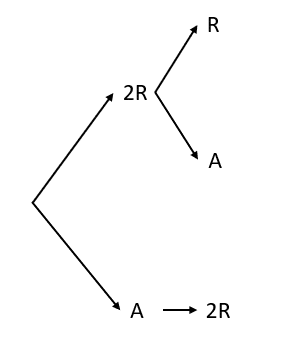
Para la tercera extracción las posibilidades son:
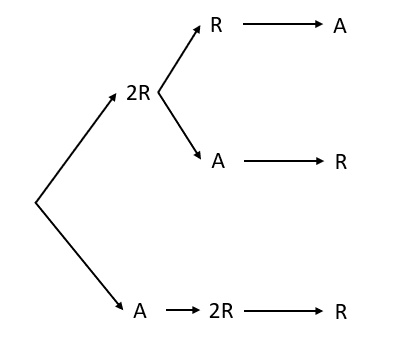
Comparando nuestra respuesta con los incisos, concluimos que la respuesta correcta es la a).
Reactivo 43
Expresar por extensión el conjunto siguiente:
A=\left\{x| x \mathrm{e}\mathrm{s}\mathrm{ }\mathrm{t}\mathrm{o}\mathrm{d}\mathrm{o}\mathrm{ }\mathrm{n}\mathrm{ú}\mathrm{m}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{ }\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{ }\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{ }\mathrm{e}\mathrm{n}\mathrm{ }\left[2, 10\right]\right\}
- A=\left\{3, 5\right\}
- A=\left\{3, 7, 9\right\}
- A=\left\{3, 5, 7, 9\right\}
- A=\left\{7, 9\right\}
Solución:
En este caso, simplemente debemos identificar a los enteros impares entre el 2 y el 10. Expandiendo el conjunto obtenemos:
\left\{2, 3, 4, 5, 6, 7, 8, 9, 10\right\}
Los números impares serían:
\left\{3, 5, 7, 9\right\}
Finalmente:
A=\left\{3, 5, 7, 9\right\}
La respuesta correcta es el inciso c).
Reactivo 44
La siguiente tabla de datos expresa los goles efectuados por el delantero de un equipo en los últimos 4 partidos.

Indique la media del conjunto de datos.
- 4
- 2
- 2.25
- 3
Solución:
Para un conjunto de datos no agrupados (como es el caso), empleamos la siguiente fórmula.
\stackrel{-}{x}=\frac{\sum {x}_{i}}{n}
Donde \sum {x}_{i} es la sumatoria de los goles efectuados en los últimos 4 partidos y n es la cantidad de partidos.
\stackrel{-}{x}=\frac{1+3+2+3}{4}=2.25
El delantero tiene un promedio de 2.25 goles por partido.
La respuesta correcta es el inciso c).
Reactivo 45
¿Cuál de las siguientes expresiones permite calcular la cantidad de arreglos de m objetos en grupos de m elementos, si se permite la repetición?
- {m}^{m}
- m!+1
- m\left(m-1\right)\left(m-2\right)
- \left(m-1\right)!
Solución:
El enunciado solicita que identifiquemos la regla de conteo que permite encontrar el total de arreglos posible. Asumimos desde un principio que importa el orden. Además, intervienen todos los elementos en los arreglos y es posible la repetición.
Esto significa que, para las m posiciones, se puede colocar cualquiera de los m objetos.
P=m\cdot m\cdot m\cdot \dots \cdot m={m}^{m}
La regla de conteo es {m}^{m} . Concluimos que la respuesta correcta es el inciso a).
Reactivo 46
Sean los conjuntos: A=\left\{1, 2, 4, 5\right\} y B=\left\{3, 2, 5, 7\right\} , calcule la diferencia B \mathrm{\Delta } A .
- \left\{3, 2, 5, 7\right\}
- \left\{\varnothing \right\}
- \left\{3, 7\right\}
- \left\{1, 3, 4, 7\right\}
Solución:
La operación del enunciado corresponde a la diferencia simétrica de conjuntos.
B \mathrm{\Delta } A=\left(B-A\right)\cup \left(A-B\right)
La diferencia de conjuntos da como resultado a los elementos del minuendo que no se encuentran en el conjunto sustraendo.
B-A=\left\{3, 7\right\}
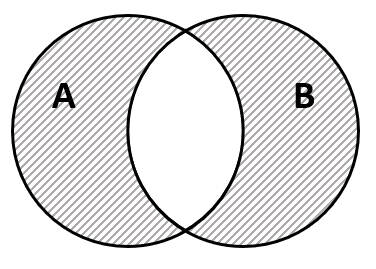
A-B=\left\{1, 4\right\}
De esta forma, la diferencia simétrica es:
B \mathrm{\Delta } A=\left\{1, 3, 4, 7\right\}
Indicamos como respuesta correcta al inciso d).
Reactivo 47
Encuentre el conjunto que origina a la siguiente partición.
S=\left\{\left\{\mathrm{1,5}\right\}, \left\{3, 9\right\}, \left\{9, 11\right\}\right\}
- \left\{1, 4, 5, 7\right\}
- \left\{1, 4\right\}
- \left\{4, 5\right\}
- \left\{1, 3, 5, 9, 11\right\}
Solución:
La partición de un conjunto A es otro conjunto cuyos elementos son {a}_{n} conjuntos, de tal forma que son subconjuntos de A y cumplen la siguiente propiedad:
A={a}_{1}\cup {a}_{2}\cup {a}_{3}\cup \dots {a}_{n}
Para encontrar al conjunto original, ejecutamos la unión de los 3 subconjuntos. Recordemos que un conjunto no tiene elementos repetidos, por tanto, el 9 debe aparecer una única vez.
A=\left\{\mathrm{1,5}\right\}\cup \left\{\mathrm{3,9}\right\}\cup \left\{\mathrm{9,11}\right\}=\left\{1, 3, 5, 9\right\}\cup \left\{\mathrm{9,11}\right\}=\left\{1, 3, 5, 9, 11\right\}
El conjunto que origina a la partición es:
A=\left\{1, 3, 5, 9, 11\right\}
La respuesta correcta es el inciso d).
Reactivo 48
¿Cuántos códigos de 2 letras se pueden formar con las vocales, teniendo en cuenta que no pueden repetirse?
- 5
- 20
- 15
- 25
Solución:
El problema se resuelve empleando alguna de las técnicas de conteo. Iniciamos identificando que se trata de una permutación/variación, ya que en los códigos importa el orden de los elementos. Por otra parte, no intervienen todos los elementos y tampoco se permite la repetición.
{P}_{2}^{5}=\frac{m!}{\left(m-n\right)!}=\frac{5\cdot 4\cdot 3\cdot 2\cdot 1}{3\cdot 2\cdot 1}=5\cdot 4=20
Se pueden formar 20 códigos de 2 vocales sin repetición.
Respuesta correcta: b).
Reactivo 49
El consejo estudiantil de una universidad mexicana está formado por 10 estudiantes de distintos años, ¿cuántas juntas directivas pueden conformarse si hay puesto para 1 presidente, 1 vicepresidente, un secretario, un vocero institucional?
- 5040
- 4050
- 3200
- 3000
Solución:
El cálculo debe realizarse aplicando alguna de las técnicas de conteo. Debido a que la junta directiva del consejo tiene una jerarquía, quedar elegido como presidente no es igual a quedar elegido como secretario, por tanto, importa el orden.
Además, queda implícito el hecho de que un mismo estudiante no puede ocupar dos puestos en la junta, no intervienen todos los elementos. Se trata de una variación ordinaria:
{P}_{4}^{10}=\frac{10!}{\left(10-4\right)!}=10\cdot 9\cdot 8\cdot 7=5040
Se pueden formar 5040 juntas directivas diferentes.
La respuesta correcta es el inciso a).
Reactivo 50
Un grupo de amigos conformado por 8 estudiantes va a una cafetería con mesas redondas y uno de ellos se pregunta: ¿de cuántas formas distintas podemos sentarnos en la mesa de la cafetería?
- 105
- 110
- 540
- 5040
Solución:
Para resolver el problema, se utiliza la ecuación de permutaciones circulares:
{P}_{c}=\left(n-1\right)!
Sustituimos a n=8 :
{P}_{c}=\left(8-1\right)!=7!=5040
El grupo de amigos puede sentarse en la mesa de 5040 formas distintas.
La respuesta correcta es el inciso d).