En este simulador vamos a resolver 50 reactivos de matemáticas para las carreras del área de ciencias sociales y administrativas muy similares a los que vendrán en tu examen de admisión al IPN.

Este examen está basado en el temario de la guía oficial y en nuestra experiencia en los últimos exámenes del IPN.
Para que sea más didáctico vamos a dividir el simulacro en 5 partes, en esta primera entrega vamos a explicar los reactivos del 1 al 10. Para consultar la segunda parte, dale clic al siguiente botón.
El siguiente es un resumen con los puntos clave del examen:
- Carreras ofertadas en IPN: 70+
- Porcentaje de aceptación: 20%
- Preguntas en el examen de admisión: 140 preguntas
- Nuevos temas: Historia e Inglés (reading comprehension)
- Tipo: selección múltiple
Carreras de ciencias sociales y administrativas
Esta es la lista completa de las carreras que forman parte de los programas académicos del área de Ciencias sociales y administrativas (consulta todas las carreras del IPN aquí):
- Contador Público
- Licenciatura en Administración Industrial
- Licenciatura en Administración y Desarrollo Empresarial
- Licenciatura en Archivonomía
- Licenciatura en Biblioteconomía
- Licenciatura en Economía
- Licenciatura en Mercadotecnia Digital
- Licenciatura en Negocios Digitales
- Licenciatura en Negocios Internacionales
- Licenciatura en Relaciones Comerciales
- Licenciatura en Turismo
- Licenciatura en Turismo Sustentable
Estructura del examen
El examen del poli se divide en dos grandes áreas; conocimientos generales, y conocimientos específicos. Recientemente, cambiaron por completo la estructura y agregaron materias al examen.
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
Nuevo examen IPN
La cantidad de reactivos ya no es la misma para todas las carreras, ahora varía según el área de estudio. Además, el examen incluye preguntas de lectura en inglés y de historia.
- Competencia escrita y competencia lectora abarcan los temas de español.
- La cantidad de reactivos ahora depende del área de la carrera.
- Se han agregado preguntas de Reading Comprahensiom (inglés) e Historia.
- El examen para todas las carreras tendrá 140 reactivos (antes eran 130 reactivos).
Temario Matemáticas CsYA
Te dejo una lista con todos los temas de matemáticas que deberás estudiar para presentar el examen de ingreso:
- Razonamiento matemático.
- Álgebra.
- Geometría y trigonometría.
- Geometría analítica.
- Probabilidad y estadística.
- Cálculo diferencial
- Cálculo integral.
Si quieres conocer el temario completo del examen de IPN ingresa al siguiente enlace:
¿Cómo resolver el simulacro?
Estos problemas han sido diseñados para que puedas practicar los temas del examen real y mejorar el tiempo que tardas en resolverlos. Incluye exámenes simulacro en tu rutina de estudio.
Las siguientes son sugerencias para tener en cuenta mientras estudias con este examen simulacro:
- Resuelve cada reactivo por tu cuenta antes de revisar las respuestas.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
- Realiza el procedimiento para que lo puedas comparar con la respuesta correcta.
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último.
Por último, y ya para comenzar, recuerda que matemáticas es solo una de las materias que tienes que estudiar, no cometas el error de estudiar únicamente la que para muchos aspirantes es la materia más difícil del examen.
Reactivo 1
Indique la fila de números que completa correctamente a la siguiente figura:

- 18, 19, 20
- 20, 21, 22
- 8, 9, 10
- 7, 8, 9
Solución:
Para completar correctamente a la cuadrícula, debemos determinar la ley de cambio entre los números. En la primera fila tenemos 1, 2, 3; pero en la segunda fila no continúa con 4, empieza en 5 y luego hace incrementos de 1 en 1.
Examinando los números de la fila inicial, nos daremos cuenta que la suma es igual a 5.
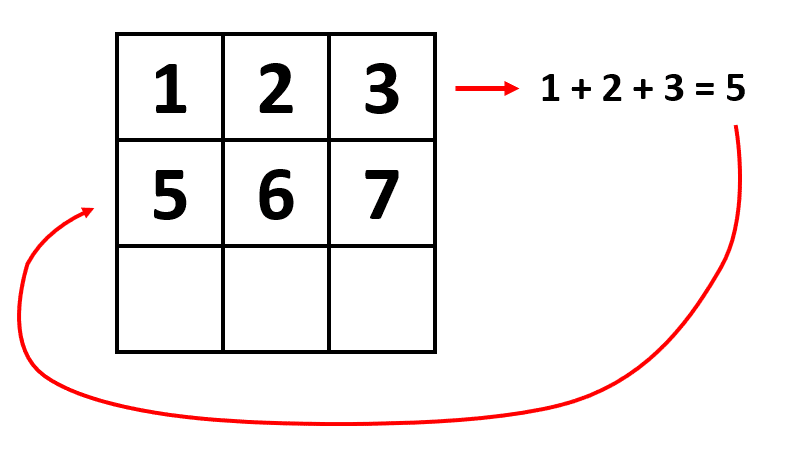
Teniendo en cuenta esto, concluimos que el primer elemento de cada fila es la suma de los elementos de la fila anterior. Obtenemos al primer elemento de la fila 3 como la suma de 5, 6 y 7.
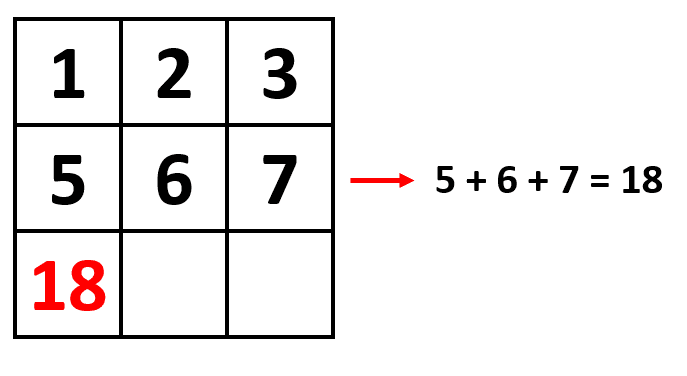
Ahora, el resto de elementos se obtienen incrementando 1.

Concluimos indicando como respuesta correcta al inciso a).
Reactivo 2
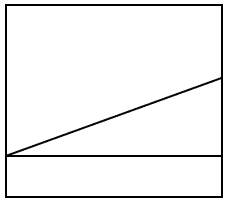
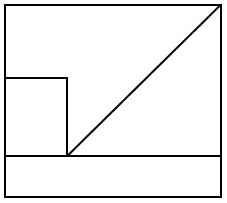
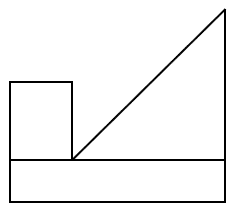
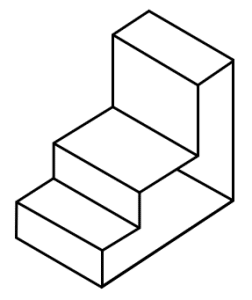
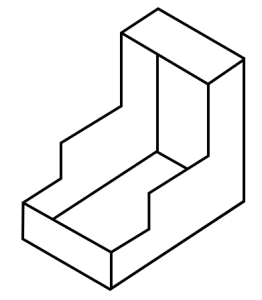
Identificar la imagen que corresponde a la vista de planta de la siguiente figura.
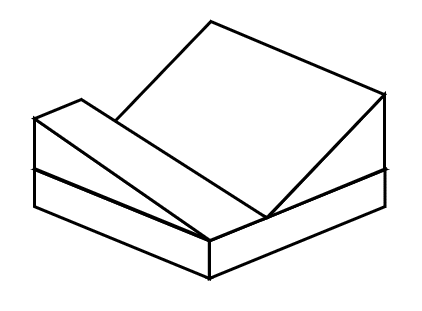
Solución:
Para responder a esta pregunta, debemos recordar el tipo de vistas que tiene un cuerpo tridimensional en dibujo técnico.
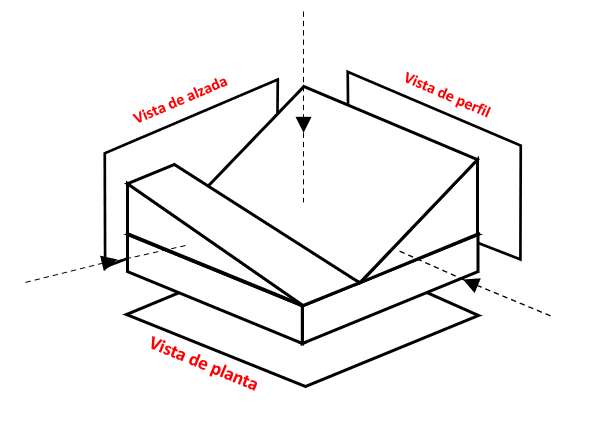
En este caso, debemos obtener la vista de planta del objeto tridimensional. Vamos a ir analizando cada uno de los elementos que se visualizan desde la planta, para obtener su representación plana.
La rampa de mayor superficie se visualiza como un rectángulo situado en la parte superior.
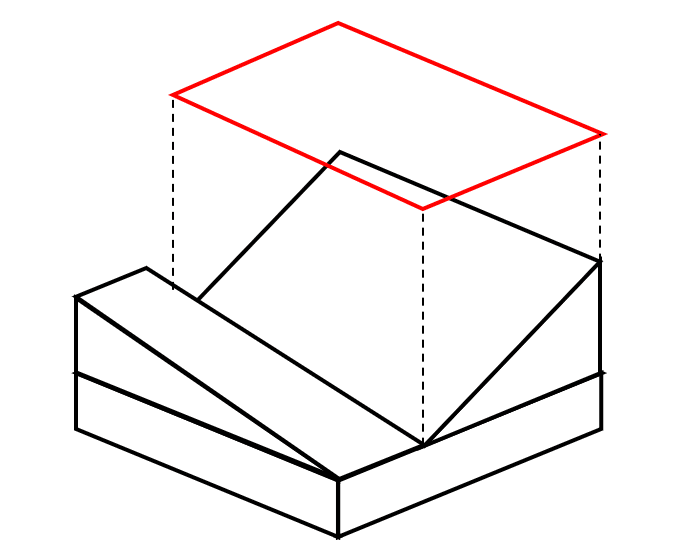
De igual forma, la rampa menor también corresponde a un rectángulo, pero en la zona inferior.
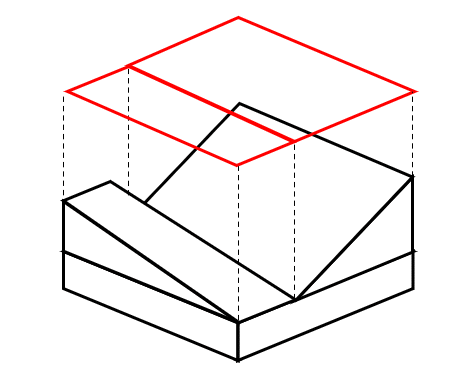
Finalmente, la vista de planta de la pieza es:

La respuesta correcta es el inciso a).
Reactivo 3
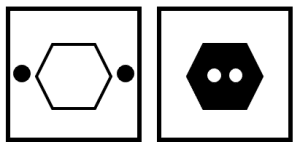
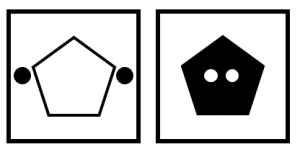
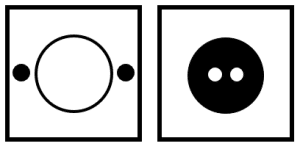
Identificar el par de figuras que dan continuación a la serie gráfica.
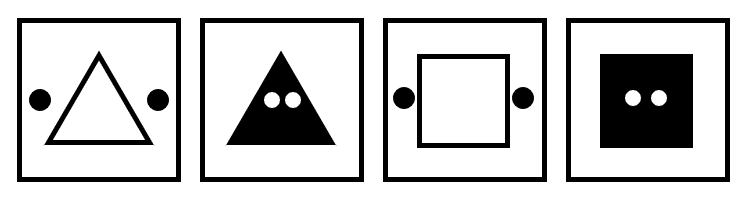
Solución:
Para resolver el problema, debemos identificar a los elementos en los términos de la serie y la forma en que cambian. Examinando los 4 términos que se muestran en la figura, podemos identificar varias características.
La figura central y los círculos cambian de color cuando se encuentran en el centro de la figura.
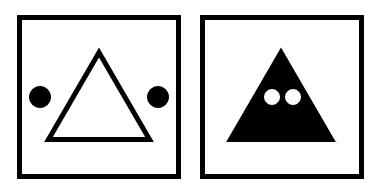
Cuando la figura central y los círculos se encuentran, el siguiente término cambia de figura. Cambia de triángulo a cuadrado, la figura incrementa 1 arista y los objetos vuelven a la posición inicial.
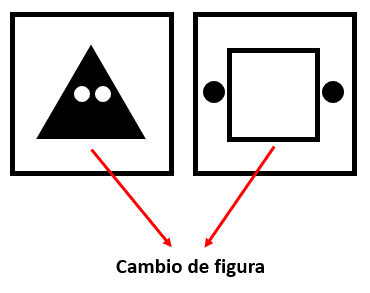
Este patrón se repite de forma cíclica.
Teniendo en cuenta estas dos leyes de cambio, podemos concluir que los siguientes dos términos poseen un pentágono que sigue el patrón cíclico ya definido.

Concluimos indicando como respuesta correcta al inciso b).
Reactivo 4
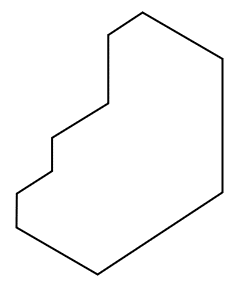
¿Cuántas aristas se deben trazar para conectar los vértices que se muestran a continuación?
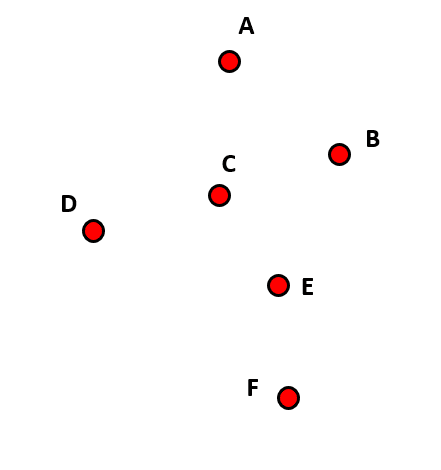
- 12
- 13
- 14
- 15
Solución:
Tenemos dos opciones para determinar las aristas que conectan a los puntos: trazar segmentos y verificar visualmente la interconexión o, emplear una fórmula. En este caso haremos uso de una ecuación, debido a que la primera opción no es viable por temas de tiempo durante el examen.
La fórmula que nos permite calcular las aristas que conectan a un conjunto de n puntos es:
A=\frac{n\left(n-1\right)}{2}
En la figura se visualizan 6 puntos, por tanto:
A=\frac{6\times 5}{2}=15 \mathrm{a}\mathrm{r}\mathrm{i}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{s}
Se deben trazar 15 aristas para interconectar a todos los puntos.
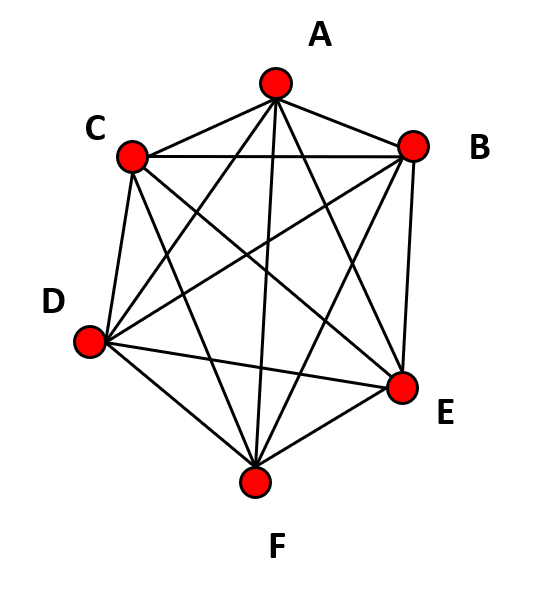
La respuesta correcta es el inciso d).
Reactivo 5
Calcule el área sombreada en la siguiente figura.

- \frac{\pi }{4}-1
- \pi -1
- \frac{\pi }{2}-1
- \frac{\pi }{8}-1
Solución:
El área sombreada en este caso tiene una disposición algo compleja. Lo primero que podemos identificar, es que ambas curvas corresponden a cuartos de círculo de radio 1.
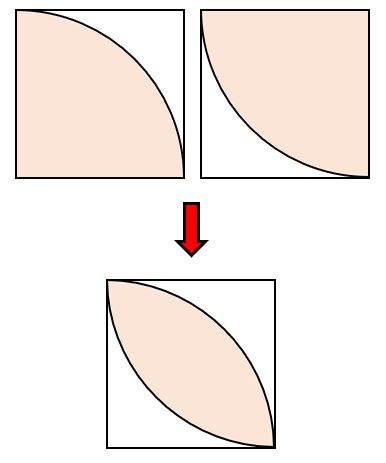
A partir de la imagen, se observa que las regiones blancas se calculan restando el área del cuarto de círculo al área del cuadrado {A}_{c} . Una vez calculada el área blanca total {A}_{b} , podemos obtener a la región sombreada como:
{A}_{s}={A}_{c}-{A}_{b}
El área total blanca puede expresarse como:
{A}_{b}=2\left({A}_{c}-{A}_{\frac{cir}{4}}\right)
Sustituyendo en la ecuación del área sombreada:
{A}_{s}={A}_{c}-2{A}_{c}+2{A}_{\frac{cir}{4}}
{A}_{s}=2{A}_{\frac{cir}{4}}-{A}_{c}
El área de un cuarto de circunferencia se calcula como:
{A}_{\frac{cir}{4}}=\frac{\pi {r}^{2}}{4}\to r=1\to {A}_{\frac{cir}{4}}=\frac{\pi }{4}
Mientras que el área del cuadrado es 1.
{A}_{s}=2\left(\frac{\pi }{4}\right)-1=\frac{\pi }{2}-1\approx 0.5708
Concluimos indicando como respuesta correcta al inciso c).
Reactivo 6
A partir del siguiente patrón, indique la figura tridimensional que se forma.
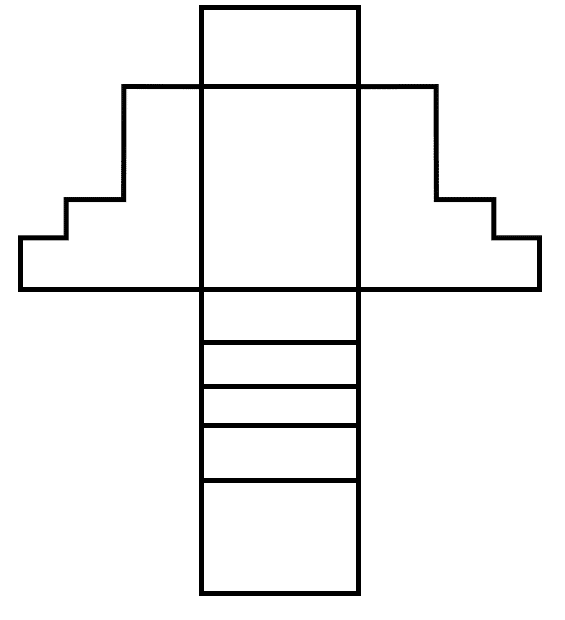
Solución:
Para encontrar la figura que se forma, debemos ir “doblando” las secciones del patrón (empleando a nuestro razonamiento espacial) hasta que todas se encuentran unidas. Los pliegos más sencillos de hacer son las dos con forma de escalera y el rectángulo superior.
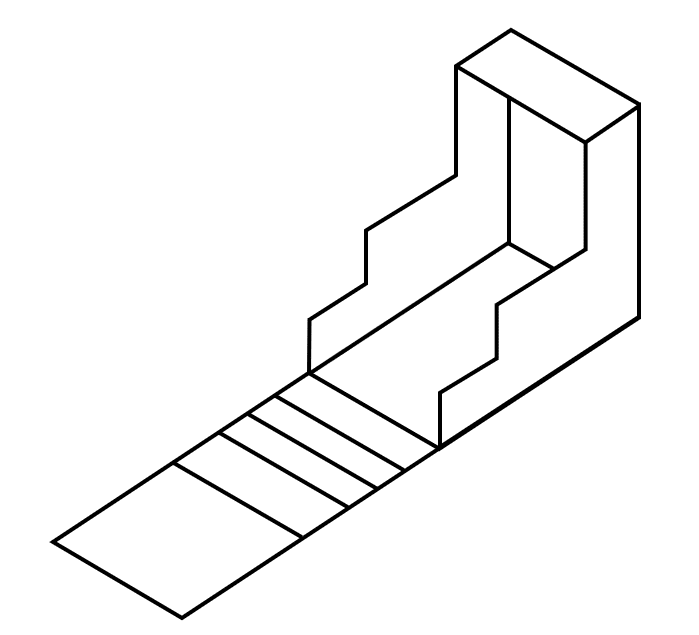
Con una perspectiva más clara de la forma que tiene la figura, culminamos los 5 pliegos restantes que corresponden a las 5 caras descubiertas de la escalera.
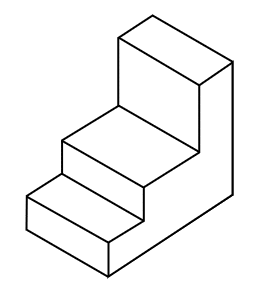
Comparando el resultado con los incisos, concluimos seleccionando al a).
Reactivo 7
Una empresa que desarrolla productos electrónicos, debe construir 400 unidades de un nuevo diseño y necesitan entregarlas en 8 semanas. Hace meses, esta misma empresa realizó 150 muestras del mismo diseño en 2 semanas con 4 líneas de producción. ¿Cuántas líneas de producción extra debe dimensionar la fábrica para cumplir con el tiempo establecido?
- 2
- 4
- 3
- 5
Solución:
Para resolver el problema, debemos emplear una regla de tres compuesta. Nuestra variable de interés es la cantidad de líneas de producción LP , mientras que los datos de referencia para las proporciones son: las unidades U y el tiempo en semanas S .
Ordenamos los datos en una tabla:

Relación entre LP y U: mientras más líneas de producción hay, mayor cantidad de unidades se pueden fabricar: relación directa.
Relación entre LP y S: a mayor cantidad de líneas de producción, menor será el tiempo de fabricación: relación inversa.
\frac{x}{4}=\left(\frac{2}{8}\right)\left(\frac{400}{150}\right)\to x=2.666
Redondeando por exceso, concluimos que la empresa necesita 3 líneas de producción.
La respuesta correcta es el inciso c).
Reactivo 8
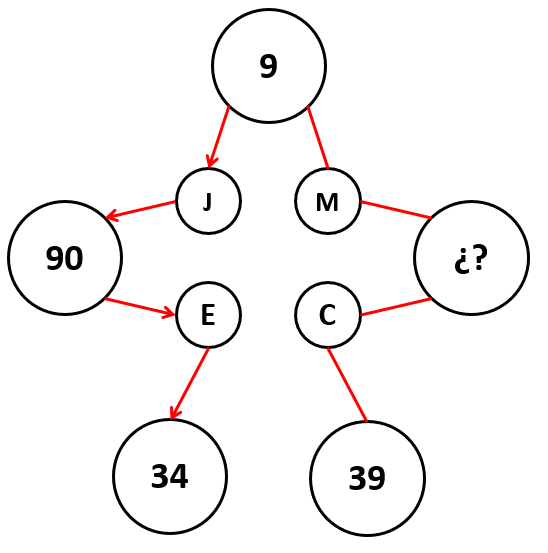
Identifique el número desconocido en el siguiente arreglo.
- 117
- 93
- 90
- 126
Solución:
En este caso, debemos establecer dos cosas: los números correspondientes a cada letra y la operación matemática que permite ir de uno a otro. De forma intuitiva, podríamos iniciar asociando a las letras su respectiva posición en el abecedario.
\mathrm{J}=10,\mathrm{ }\mathrm{E}=5,\mathrm{ }\mathrm{M}=13,\mathrm{ }\mathrm{C}=3
Sustituimos en la imagen a estas cantidades:

Para llegar desde el 9 hasta el 90 pasando por el 10 debemos multiplicar.
9\cdot 10=90
Ahora, para ir hasta el 34 partiendo del 90 no puede ser ni sumando ni restando, mucho menos multiplicando. Probamos con la división:
90÷5=34
De esta forma, las operaciones entre las cantidades son: multiplicar y dividir.
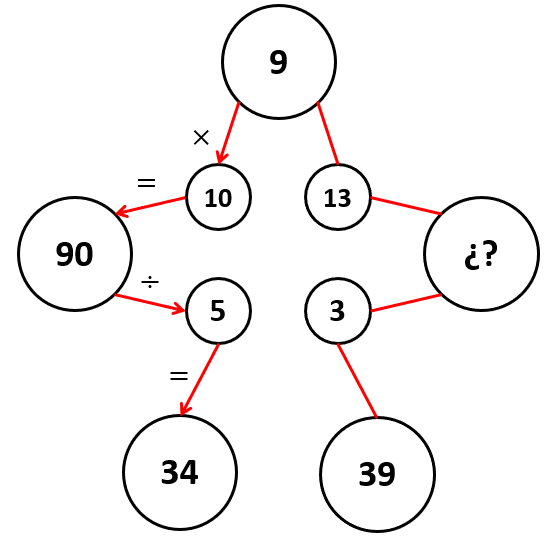
Multiplicando el 9 con el 13, podremos completar el gráfico:
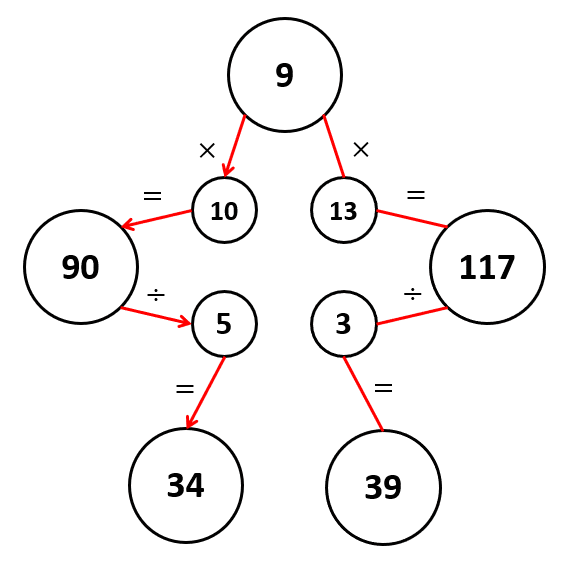
Concluimos que la respuesta correcta es el inciso a).
Reactivo 9
Una empresa va a importar un cargamento de dispositivos electrónicos para su posterior comercialización en el territorio nacional. El cargamento contiene 100 paquetes de resistencias eléctricas, 150 de condensadores, 120 de transistores, 300 de diodos emisores de luz y 50 con dispositivos Arduino.
Si el peso de cada paquete es como se indica a continuación:
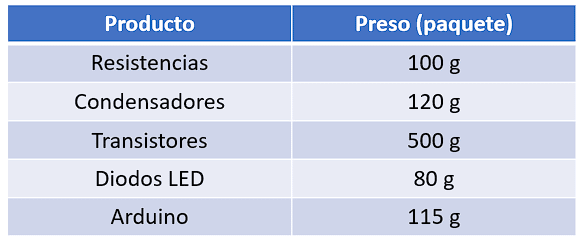
Calcule el cobro neto del envío, si el costo por libra es de 100 pesos. Considere que: 1 \mathrm{l}\mathrm{b}=453.6\mathrm{ }\mathrm{g} .
- 26000$
- 25960$
- 30000$
- 19789$
Solución:
Para encontrar el cobro total del envío, primero debemos calcular el peso de toda la encomienda. Esta se calcula como la suma de los productos de los paquetes por su correspondiente peso.
{P}_{neto}=R\cdot {P}_{R}+C\cdot {P}_{C}+T\cdot {P}_{T}+DL\cdot {P}_{DL}+A\cdot {P}_{A}
Sustituimos los valores dados en la tabla.
{P}_{neto}=\left(100\right)\left(100\right)+\left(150\right)\left(120\right)+\left(120\right)\left(500\right)+\left(300\right)\left(80\right)+\left(50\right)\left(115\right)
{P}_{neto}=117750 \mathrm{g}
Ahora, transformamos a libras.
117750\mathrm{ }\mathrm{g}\cdot \frac{1 \mathrm{l}\mathrm{b}}{453.6 \mathrm{g}}=259.6 \mathrm{l}\mathrm{b}
Finalmente, calculamos el costo de la encomienda.
\mathrm{C}\mathrm{o}\mathrm{s}\mathrm{t}\mathrm{o}=\left(259.6\right)\left(100\right)=25960 \mathrm{\$}
Concluimos indicando como respuesta correcta al inciso b).
Reactivo 10
Calcular el valor de x a partir de la siguiente expresión.
{\mathrm{log}}_{\sqrt{7}}\left(2{x}^{2}-1\right)=2
- x=2
- x=-2
- x=\pm 2
- x=-\frac{1}{2}
Solución:
Para resolver esta ecuación logarítmica, debemos emplear la definición de logaritmo.
{\mathrm{log}}_{b}a=c\to {b}^{c}=a
Llevando esto al ejercicio tenemos que:
a=2{x}^{2}-1, b=\sqrt{7}, c=2
Aplicando la definición nos queda:
{\sqrt{7}}^{2}=2{x}^{2}-1\to 7=2{x}^{2}-1
2{x}^{2}=8\to {x}^{2}=4\to x=\pm 2
Sustituimos los valores de x en el argumento del logaritmo para comprobar que no se anule o tenga un resultado negativo.
x=2\to 2{\left(2\right)}^{2}-1=7
x=-2\to 2{\left(-2\right)}^{2}-1=7
Concluimos que la respuesta correcta es el inciso c).